Landau-Vishkin
基础算法
假设我们有两个字符串:![]()
![]() ,每个字符串由A C G T四个字母组成。
,每个字符串由A C G T四个字母组成。
在两个字符串上,都有三种可能的编辑操作(突变):
- 删除某个字符
- 在某个位置插入字符
- 改变某个字符
每一个编辑操作都有惩罚值。用D(R,B)表示字符串R和B的最小编辑距离(总惩罚值)。
在这里,我们将三种编辑操作的惩罚值都设为1。
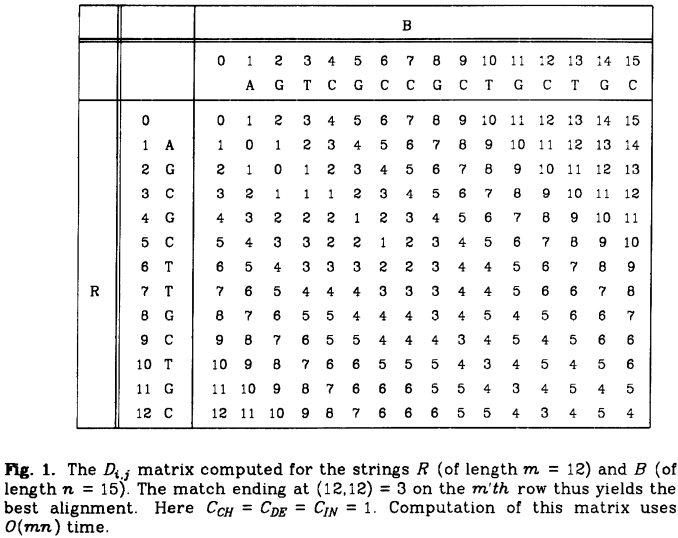
定义矩阵D,X维和Y维分别表示字符串B和R。在矩阵的![]() 上,我们尝试对两个字符串对应位置的字符进行匹配,并计算相应位置的分数。
上,我们尝试对两个字符串对应位置的字符进行匹配,并计算相应位置的分数。
在矩阵上DP的过程实际上具有生物学意义。比如,上下或者左右移动意味着插入或者删除,在对角线上移动意味着匹配/失配。
很明显,在对角线上移动比左右/上下移动更容易找到符合条件的匹配。
示例图片:
伪代码:

算法优化
上面的算法的时间复杂度为O(m^2)。
在上一个算法的推导过程中,我们可以发现:在矩阵上DP的过程中,偏离中心对角线很远的元素基本不会符合答案要求。
设k为最大的惩罚值,通过限制搜索过程中D中元素的大小,只要大于k就放弃该元素,就可以达到优化时间复杂度到O(km)的效果。
在此基础上,考虑能否通过优化DP矩阵的两个维度,通过直接限制搜索空间的方法将空间复杂度也优化到O(km)。
可以发现,一个比较好的匹配总是沿对角线进行的。而且,如果遍历每一条对角线,一定能找到最终匹配。
定义差异值e(e<=k)作为新矩阵的一个维度。考虑到算法基础是以对角线为中心,向两边拓展差异值<=k,那么对角线编号应当作为矩阵的另一个维度。
我们将计算的矩阵重新定义为![]() ,其中d代表第几个对角线,e代表当前差异值。
,其中d代表第几个对角线,e代表当前差异值。
可以发现,目前缺少一个代表"位于对角线的哪个位置"的元素。那么,就将元素值设为当前位于模式串的第几个字符,也就是之前D矩阵的行数即可。
现在,L矩阵上元素的值指对于第d个对角线,在差异值为e的情况下,最多能拓展到第几行。
接下来,考虑如何计算这个矩阵。
思考对角线之间的关系,可以发现:对于任意一条对角线,可以通过其相邻两条对角线当前拓展到的最大行数+1更新这一条对角线能拓展到的最大行数。这是因为通过一个插入/删除操作可以使两条相邻对角线上的对齐转化到当前对角线上。
因此,对于![]() ,只有
,只有
- 位于同一条对角线且差异值比他小1的元素
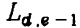 +1
+1 - 在上面的一条对角线上,
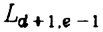 +1
+1 - 在下面的一条对角线上,
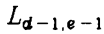 +1
+1
可以更新它的值。
伪代码
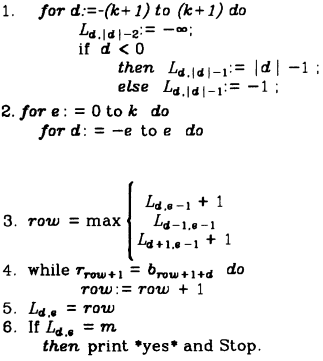
C++代码

#include<cstdio> #include<iostream> #include<cmath> #include<cstring> #include<map> const int INF = 20000000; const int MAXN = 2000; const int MAXK = 100; void setValue(int L[MAXN][MAXK], int i, int j, int value) { L[i + (MAXN >> 1)][j + (MAXK >> 1)] = value; } int getValue(int L[MAXN][MAXK], int i, int j) { return L[i + (MAXN >> 1)][j + (MAXK >> 1)]; } bool sameChar(char r[], char b[], int rIndex, int bIndex,int lenB,int lenR) { rIndex--; bIndex--; if (rIndex == 0 && bIndex == 0)return 1; if (rIndex < 0 || bIndex < 0) { printf("WRONG!"); return 0; } if (rIndex >= lenR || bIndex >= lenB)return 0; return r[rIndex] == b[bIndex]; } bool isSame(char r[], char b[],int lenB,int lenR) { if (lenR != lenB)return 0; for (int i = 0; i < lenR; i++) { if (r[i] != b[i])return 0; } return 1; } void printAll(int L[MAXN][MAXK], int k) { // 第几个对角线 for (int i = -k; i <= k; i++) { // 差异值 for (int j = -k; j <= k; j++) { printf("L[%d][%d]=%d ", i, j, getValue(L, i, j)); } printf("\n"); } } void init(int L[MAXN][MAXK], char r[], char b[], int k) { for (int d = -(k + 1); d <= k + 1; d++) { setValue(L, d, abs(d) - 2, -INF); if (d < 0) { setValue(L, d, abs(d) - 1, abs(d) - 1); } else { setValue(L, d, abs(d) - 1, -1); } } } #define scanf_s scanf int max(int a,int b){ if(a>b)return a; return b; } int main() { // 两个字符串 char r[MAXN], b[MAXN]; int k; int dp[MAXN][MAXK]; memset(dp, 0, sizeof(dp)); printf("R Input:"); scanf_s("%s", &r); printf("B Input:"); scanf_s("%s", &b); printf("k:"); scanf_s("%d", &k); init(dp, r, b, k); int lenB=strlen(b); int lenR=strlen(r); if (k == 0) { if (isSame(r, b,lenB,lenR)) { printf("yes\n"); } else { printf("no\n"); } return 0; } // 遍历每一个差异值 for (int e = 0; e <= k; e++) { // 遍历每一个差异值的所有对角线 for (int d = -e; d <= e; d++) { int row = max(getValue(dp, d, e-1) + 1, max(getValue(dp, d - 1, e - 1), getValue(dp, d + 1, e - 1) + 1)); while (sameChar(r, b, row + 1, row + 1 + d,lenB,lenR)) { row++; } setValue(dp, d, e, row); if (getValue(dp, d, e) == lenR) { printf("yes\n"); //printAll(dp, k); return 0; } } } //printAll(dp, k); printf("no\n"); return 0; }
对拍
数据生成

#include<cstdio> #include<iostream> #include<cmath> #include<string> #include<algorithm> #include<ctime> #include<map> const int INF = 20000000; const int MAXN = 2000; using namespace std; int min(int a,int b){ if(a<b)return a; return b; } string randomChar(){ int opt=rand()%4; switch(opt){ case 0: return "A"; case 1: return "T"; case 2: return "C"; case 3: return "G"; } } string createSequence(string str,int len){ for(int i=0;i<len;i++){ str+=randomChar(); } return str; } string insert(string str){ int len=str.length(); int index=rand()%len; return str.insert(index,randomChar()); } string replace(string str){ int len=str.length(); int index=rand()%len; char oldChar=str[index]; while(oldChar==str[index]){ str=str.replace(index,1,randomChar()); } return str; } string _delete(string str){ int len=str.length(); int index=rand()%len; return str.erase(index,1); } string randomOpt(string origin,int optNum){ string tmp=origin; for(int i=1;i<=optNum;i++){ int opt=rand()%3; switch(opt){ case 0: tmp=insert(tmp); continue; case 1: tmp=replace(tmp); continue; case 2: tmp=_delete(tmp); continue; } } return tmp; } int main() { srand((int)time(NULL)); int len=rand()%10+5; int optNum=rand()%(min(40,len-3)); string b="",r=""; b=createSequence(b,len); r=randomOpt(b,optNum); int is=rand()%2; int delta=rand()%3; if(is==0){ delta*=-1; } if(r.length()>b.length()){ printf("%s\n",b.c_str()); printf("%s\n",r.c_str()); printf("%d\n",optNum+delta); }else{ printf("%s\n",r.c_str()); printf("%s\n",b.c_str()); printf("%d\n",optNum+delta); } return 0; }
正确代码

#include<cstdio> #include<iostream> #include<cmath> #include<cstring> #include<algorithm> #include<map> const int INF = 20000000; const int MAXN = 2000; void printAll(int dp[MAXN][MAXN],int lenR,int lenB) { for (int i = 0; i <= lenR; i++) { for (int j = 0; j <= lenB; j++) { printf("%d ", dp[i][j]); } printf("\n"); } } int min(int a,int b){ if(a<b)return a; return b; } int dp[MAXN][MAXN]; int main() { // 涓や釜瀛楃涓? char r[MAXN], b[MAXN]; int k; printf("R Input:"); scanf("%s", &r); printf("B Input:"); scanf("%s", &b); printf("k:"); scanf("%d", &k); int lenR = strlen(r), lenB = strlen(b); dp[0][0] = 0; for (int j = 1; j <= lenB; j++) { dp[0][j] = j; } for (int i = 1; i <= lenR; i++) { dp[i][0] = i; } for (int i = 1; i <= lenR; i++) { for (int j = 1; j <= lenB; j++) { int tmp = dp[i - 1][j - 1]; if (r[i - 1] != b[j - 1])tmp++; dp[i][j] = min(dp[i - 1][j] + 1, min(dp[i][j - 1] + 1, tmp)); } } int minn=INF; for (int i = 1; i <= lenB; i++) { minn = min(minn, dp[lenR][i]); } // printAll(dp, lenR, lenB); if (minn <= k) { printf("yes\n"); }else { printf("no\n"); } return 0; }



