并查集与Kruskal算法(最小生成树)
基本并查集建立
并查集是一种合并不相交集合的数据结构 ，常用在寻找图中是否存在环路
建立并查集就是在建立一个尽量平衡的树。边建立边检测是否存在环路
最重要的两点：
- 找到根节点 find_root(x)
- 合并两棵树 union(xTree,yTree)
#include <stdc++.h>
using namespace std;
#define VERUTICES 6 //结点数
int find_root(int x,int parent[]){
int x_root=x;
while(parent[x_root]!=-1){
x_root=parent[x_root];
}
return x_root;
}
//return : 1 --success
// 0 --fail
int union_vertices(int x,int y,int parent[]){
int x_root=find_root(x,parent);
int y_root=find_root(y,parent);
if(x_root == y_root){
return 0;
}else{
parent[x_root]=y_root;
return 1;
}
}
int main(){
int parent[VERUTICES]={0};
//二维数组存储边
int edges[5][2]={
{0,1},{1,2},{1,3},{3,4},{2,5}
};
memset(parent,-1,sizeof(parent)); //初始化父结点数组
//遍历6条边
for(int i=0;i<5;i++){
int x=edges[i][0];
int y=edges[i][1];
if(union_vertices(x,y,parent)==0){
cout<<"存在环路"<<endl;
return 0;
}
}
cout<<"无环路"<<endl;
return 0;
}
压缩路径
再进一步压缩路径，使其更加平衡：
我们需要在以上代码基础上添加：
1.rank 数组 标记根节点所在的树深高度，并维护（注：rank[]只有在两个集合树高度相等时拼接一起才需要+1）
2.下列代码 实际每个节点的rank[]值代表的是当前节点在树的高度-1
#include <stdc++.h>
using namespace std;
#define VERUTICES 6 //结点数
int find_root(int x,int parent[]){
int x_root=x;
while(parent[x_root]!=-1){
x_root=parent[x_root];
}
return x_root;
}
//return : 1 --success
// 0 --fail
int union_vertices(int x,int y,int parent[],int rank[]){
int x_root=find_root(x,parent);
int y_root=find_root(y,parent);
if(x_root == y_root){
return 0;
}else{
if(rank[x_root]>rank[y_root]){
parent[y_root]=x_root;
}else if(rank[x_root]<rank[y_root]){
parent[x_root]=y_root;
}else{
parent[x_root]=y_root;
rank[y_root]++;
}
return 1;
}
}
int main(){
int parent[VERUTICES]={0};
int rank[VERUTICES]={0};
//二维数组存储边
int edges[5][2]={
{1,2},{3,4},{2,5},{1,3},{0,1}
};
memset(parent,-1,sizeof(parent)); //初始化父结点数组
//遍历5条边
for(int i=0;i<5;i++){
int x=edges[i][0];
int y=edges[i][1];
if(union_vertices(x,y,parent,rank)==0){
cout<<"存在环路"<<endl;
return 0;
}
}
cout<<"无环路"<<endl;
for(int i=0;i<5;i++){
cout<<i<<": "<<rank[i]<<endl;
}
return 0;
}
ps:额这个案例边数组比较特殊，大家可以改一改顺序，会得出不同rank值
与Kruskal算法(最小生成树)之间的关系
Kruskal算法：针对有 n 个结点的带权无向图，按边的权值从大到小排，，每次从其中取出一条边，两个结点（注意是两个不同连通分量的结点，也就是不能成环）。最后生成 n-1 条边的 最小生成树(边最少包含所有顶点)。
在克鲁斯卡尔算法中，我们需要将两个不同连通分量合并，不能有环。
在并查集中，我们合并的是两个不同的树型区域，不能有环。
可以发现，克鲁斯卡尔最重要的合并操作 在code 实现上正是由并查集这一数据结构完成的。
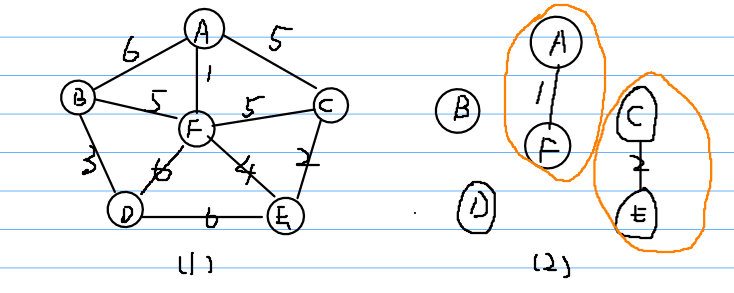
譬如图一是所有结点权值，将所有结点独立，在几次选边合并操作后变为图二，此时合并图二两个连通分量可以用并查集。
