截止日期

问题描述

某学科老师布置了n个题目，每个题目都有相应的分数及截止日期。各个题目的分数及截止日期可能并不相同。对某题目而言，如果在该题目的截止日期前完成则可获得对应的分数，否则无法得分。假设每个题目均需要花费一天的时间来完成，这期间无法完成其他题目。请你设计算法指定题目的完成计划，从而使总的得分最大。

下面给出一个包含了7个题目及相应的分数、截止日期的实例：

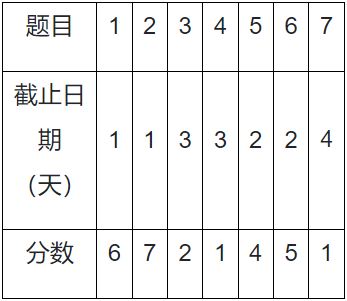
 对该实例而言，得分最大的作业完成方案为花费4天时间依次完成题目2,6,3,7。得分为15。

输入格式

输入数据第一行为一个整数n (0≤n ≤10000), 表示题目数目
之后n行各有两个整数, 第i行为 pi, di (1≤pi, di≤10000)，分别表示第i个题目的分数和截止时间

输出格式

一个整数, 为当前条件下的最大得分

样例输入

4 

50 2 

10 1 

20 2 

30 1

样例输出

80

题解

假设有k道题目在第i天截止，为了得分最大，显然优先选得分高的题

考虑按截止日期从小到大，分数从高到低排序，这样可以保证同一截止日期先做分数高的题

这样可以过样例，但是对于如下数据：

7

1 2

1 2

5 5

5 5

5 5

5 5

5 5

显然最优解是5天做5道5分的题，但是上述算法会用前两天做截止日期为2的那两题，因为上述算法优先考虑截止日期，可能会有足够多的高分题截止日期很晚，但是做完这些题会导致一些截止日期早的低分题做不了，而上述算法会优先做截止日期早的题，即可能把最优解中不用做的题做了，导致了错误答案

由此可知正确算法应该优先考虑高分再考虑截止日期

考虑对题目按分数从高到低排序

显然一道题能做的最晚时间是它的截止日期

但是轮到这道题时它的截止日期可能已经被其它题占了，这时只能一天天往前推到最晚的没被占用的一天

一道题不在最优解中的条件是从它的截止日期开始一直往前推到第0天都被占用了

判断一道题不在最优解中的时间复杂度是它的截止日期的大小

截止日期最大为10000，题目总数最多为10000，假设有10000道题每道题截止时间都是10000，每道题都往前推所需时间为0+1+2+……+9999≈10000²,

也就是说最坏情况下可能会超时

考虑并查集压缩路径，f[i]表示截止日期为i的最晚的没被占用的天（即不超过i的最晚的未被占用的日期），初始时f[i]=i，当f[i]被占用时将f[i]更新为find(f[i]-1) （find为路径压缩函数），这样可以用接近O（1）的时间找到截止时间为i的没被占用的最晚的时间，当f[i]为0时就表示从第0天到第i天都被占用了

 

 

#include <algorithm>
#include <cstdio>
int n,t,ans;
int f[10005];
struct node{
    int p,d;
}a[10005];
bool cmp(node x,node y)
{
    return x.p>y.p;
}
int find(int x)
{
    if (f[x]==x) return x;
    return f[x]=find(f[x]);
}
int main()
{
    int i,j,x;
    scanf("%d",&n);
    for (i=1;i<=n;i++)
      scanf("%d%d",&a[i].p,&a[i].d);
    std::sort(a+1,a+n+1,cmp);
    for (i=1;i<=10000;i++)
      f[i]=i;
    t=1;
    for (i=1;i<=n;i++)
    {
        x=find(a[i].d);
        if (x) 
          ans+=a[i].p,
          f[x]=find(f[x]-1);
    }
    printf("%d",ans);
    return 0;
}