"蔚来杯"2022牛客暑期多校训练营4 N-Particle Arts

问题描述

In a confined NIO space, there are n NIO particles, the i-th of which has a_i​ joule energy. The NIO particles are very special as they keep colliding with each other randomly. When one particle carrying energy a joule collides with another particle carrying energy b joule, they will be annihilated and produce two new particles carrying the energy of a AND b  and a OR b respectively. Here AND and OR mean bitwise AND and OR operation respectively.
The variance of the energy of these particles is obviously not decreasing, but unfortunately, the space here is too small for the author to write down his proof. After enough time the variance of the energy of these particles converges to a stable value. Can you find this value?
The variance of n numbers is defined as follows.

输入格式

The first line contains an integer n (2≤n≤10⁵), indicating the number of particles.
The second line contains n integers a₁,a₂,…,a_n (0≤ai​<2¹⁵), indicating the enegery of the particles.

输出格式

Output a irreducible fraction a/b (b>0) in the form of a/b that represents the answer. You should ensure that gcd⁡(a,b)=1 or when a=0, b should be 1.

样例输入

5
1 2 3 4 5

样例输出

54/5

提示

Warm tip: Please note the use of data types.

题解

模拟样例可知最后方差不变时，任意两个数进行计算都不会使序列发生改变

将样例所给数字全部转换成二进制，可以发现，最后所有数字不再改变时，所有的1都被尽可能移到一起

 

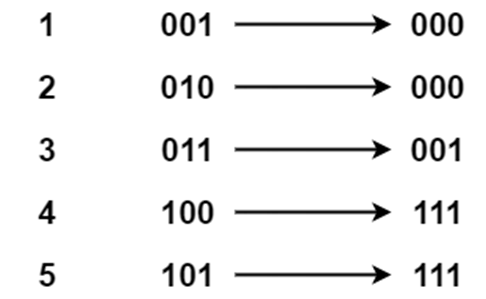
考虑统计二进制下1和0的个数，将1尽可能的移到一起，即可生成最后不再改变的序列，答案即为该序列的方差

 

 

#include <cstdio>
#define ll long long
int n,a[100005],cnt[20];
ll b[100005],sum,m,ans;
ll gcd(ll x,ll y)
{
    return y?gcd(y,x%y):x;
}
int main()
{
    int i,j,k;
    scanf("%d",&n);
    for (i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        for (k=0;k<15;k++)
        {
            if ((1ll<<k)&a[i])
              cnt[k]++;
        }
    }
    ll x,s=0;
    for (i=1;i<=n;i++)
    {
        for (j=0;j<=19;j++)
        {
            if (cnt[j])
              b[i]+=(1ll<<j),
              cnt[j]--;
        }
        sum+=b[i];
        s+=b[i]*b[i];
    }    
    ans=s*n-sum*sum;
    x=gcd(ans,1ll*n*n);
    printf("%lld/%lld",ans/x,1ll*n*n/x);
    return 0;
}