"蔚来杯"2022牛客暑期多校训练营1 - D Mocha and Railgun

问题描述

There is a candy store near Mocha's school. It's said that the storekeeper, Dagashiya, can cast the railgun spell. To be the most powerful Mahou Shoujo, Mocha asks Dagashiya to teach her the railgun spell.
To test her mastery of this spell, Mocha creates a circular wall C whose center is (0,0). The railgun spell has a base segment AB with length 2d. When it is cast, a point P on the circular wall will be destroyed if and only if it meets the following conditions:

         1、The projection of point P on line AB lies on the segment AB (inclusive).

         2、A,B,P make a counterclockwise turn, that is to say 

Mocha chooses a point Q which strictly lies in the circle and sets Q as the center of the base segment. Then Mocha will choose an angle α arbitrarily and rotate the base segment around Q by α. Because Mocha is a rookie of the spell, the endpoints of the base segment will always lie in C strictly, which means the distance from Q to the wall C is greater than d.
Mocha wants to know the maximum length of the wall that can be destroyed in one cast.
You can see the note for better understanding.

输入格式

The first line is an integer T (1≤T≤10⁵) — the number of test cases.

In each test case, the first line is an integer r (1≤r≤10⁹ ) — the radius of the circular wall C.

The next line contains three integers x_Q，y_Q，d — the coordinates of the point Q and a half of the length of the base segment.

输出格式

For each test case, print a real number in a single line, denoting the maximum length of the wall that Mocha can destroy in one cast. Your answer will be considered equal to the correct answer when their absolute or relative error doesn't exceed 10⁻⁶.

样例输入

1
2
0 0 1

样例输出

2.094395102393

提示

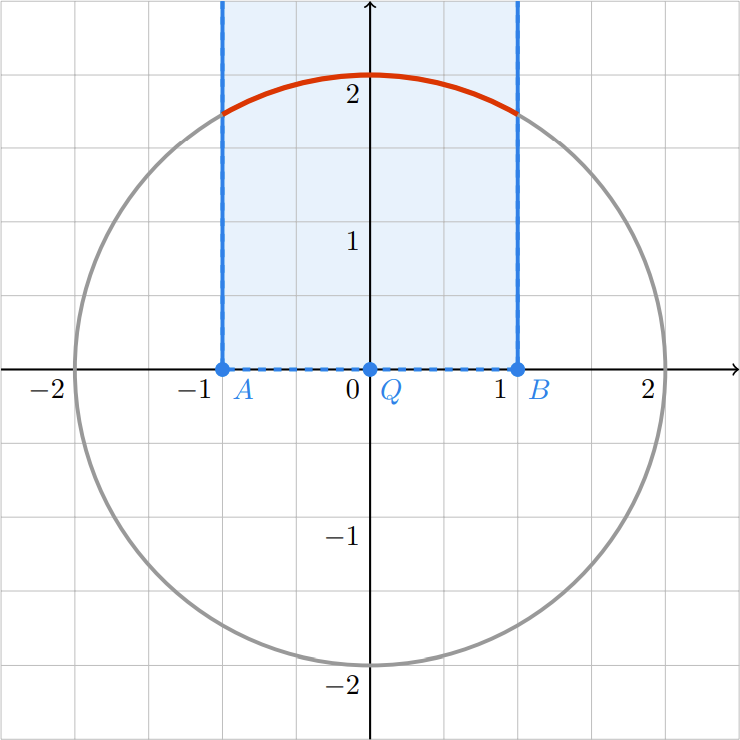
In the picture above, the blue lines are the boundaries of the railgun spell. The red arc is the wall being destroyed.

题解

给定圆心在原点的圆和圆内一点Q，求以Q为终点长度为2d的线段在圆弧上最长的投影

 

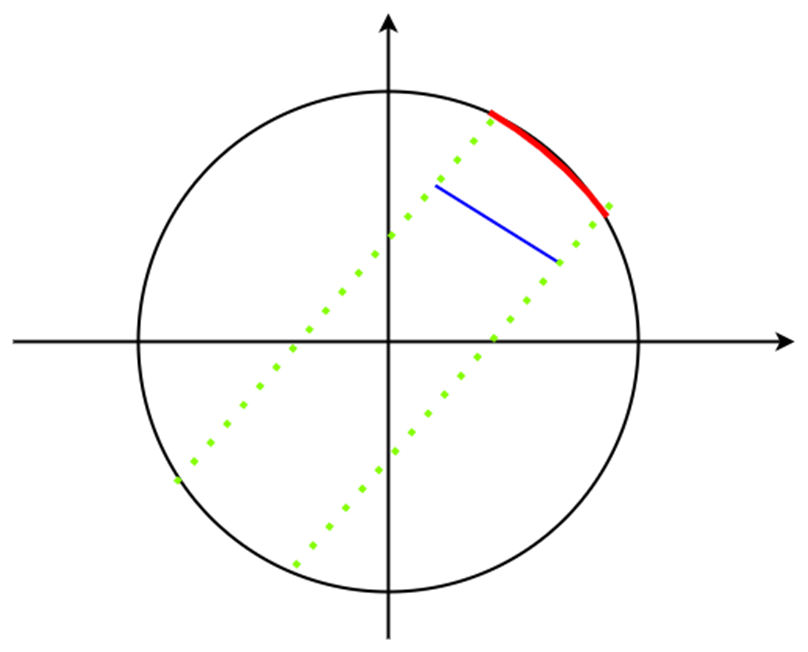
若已知线段的位置，可以通过角度关系求出线段所对圆心角的度数，然后通过反三角函数求出圆心角对应的弧长即为最长投影

大胆猜测线段的位置一定是一个特殊位置，然后可以利用特殊位置关系求出圆心角，不是特殊位置的话好像求不出来

当圆心和Q连线平行于线段（即和半径重合）时，那个位置看起来不太好求

于是再次大胆猜测圆心和Q的连线垂直于线段，就可以通过垂直关系求出对应圆心角

 

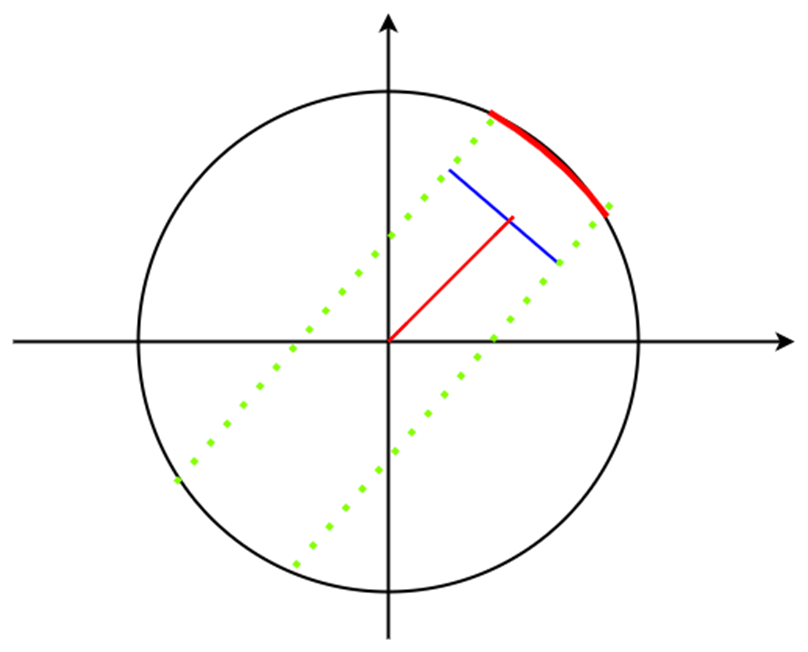
如图，线段在两条虚线间的任何位置对应的弧长都是一样的，为了方便求解，可以将线段移动成为弦，通过反正弦函数求出角α，即半个弧长所对圆心角，从而可求出弧长

 

就这样过了样例，感觉代码也没什么问题了，然而提交死活过不去，，各种精度之类的细节也检查过了，不知道哪里错了。。。

后来查了题解发现是猜错了。。。。。

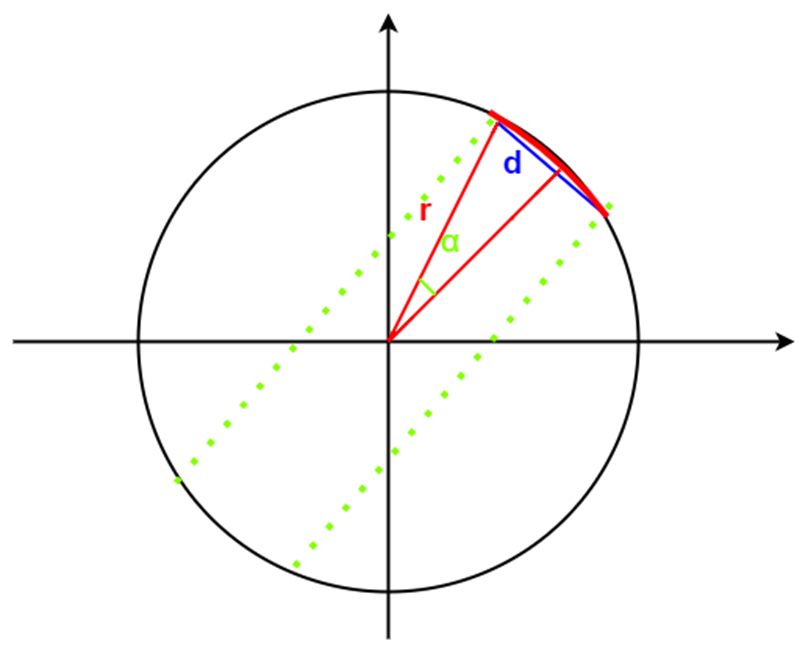
事实上，圆心和Q的连线垂直于线段时，线段即为弦长，圆心和Q的连线平行于线段时，弦长为以线段为直角边的三角形的斜边，此时的弦长比线段长度更长，所以当圆心和Q的连线平行于线段时弧长最长

     

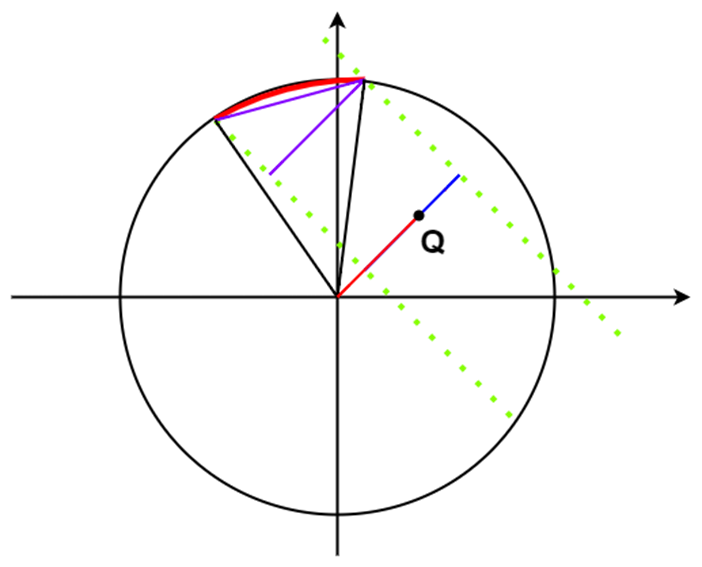
此时我们所求的圆弧所对圆心角可看成两个角之差

 

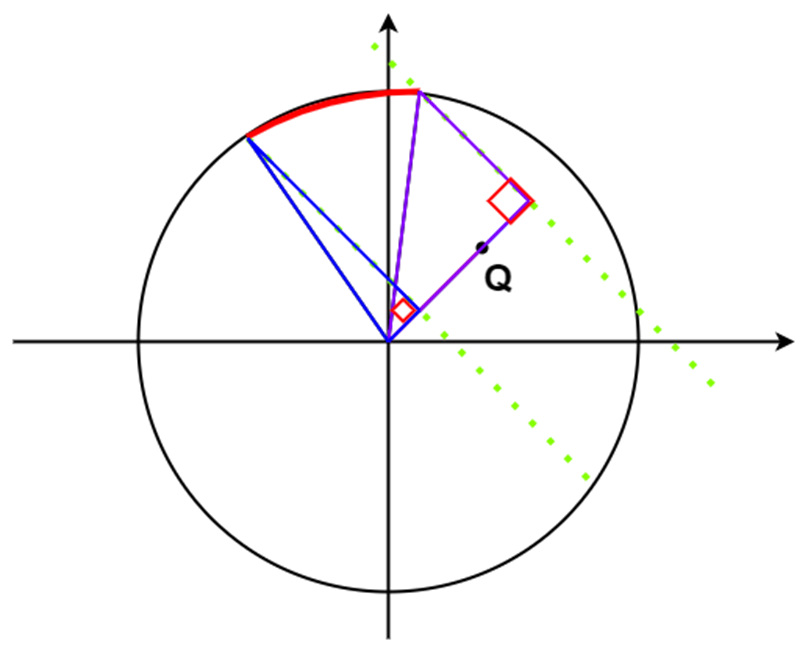
图中两个直角三角形的斜边长都为圆的半径r，通过反余弦函数可求出两个圆心角，相减得到所求圆弧对应的圆心角，从而求出圆弧长

就是说大胆猜测顾名思义不一定是对的。。。

实在不会证明的话可以试试多猜几个

感觉代码各种细节都考虑到了还不知道为什么过不了的话就可能是猜错了。。。

 

 

#include <cstdio>
#include <cmath>
using namespace std;
int T;
double r,x,y,d;
int main()
{
    double a,l,b;
    scanf("%d",&T);
    while (T--)
    {
        scanf("%lf",&r);
        scanf("%lf%lf%lf",&x,&y,&d);
        l=sqrt(x*x+y*y);
        a=acos((l-d)/r);
        b=acos((l+d)/r);
        printf("%.10lf\n",(a-b)*r);
    }
    return 0;
}