算数基本定理

算数基本定理

定义

任何一个大于1的自然数N，如果N不为质数，都可以唯一分解成有限个质数的乘积

  ，

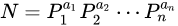这里 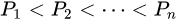均为质数，其诸指数a_i是正整数。

 

这样的分解称为N的标准分解式。

 

应用

（1）一个大于1的正整数N，如果它的标准分解式为：

    ，

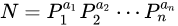   那么它的正因数个数为

    

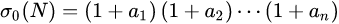
（2）它的全体正因数之和为

               

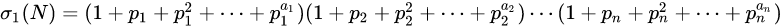
当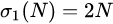时就称N为完全数。 是否存在奇完全数，是一个未解决之猜想。

（3）利用算术基本定理可以重新定义整数a和b的最大公因子（a，b）和最小公倍数[a，b]，并证明ab=(a,b)×[a,b]。

（4）此外还可证明根号2是无理数等等。

（5）证明素数个数无限。