【POJ1061】【洛谷P1516】青蛙的约会

问题描述

输入格式

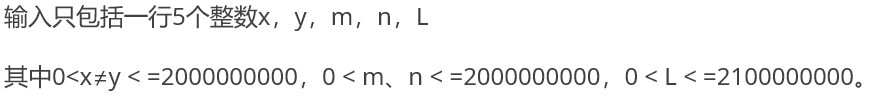
输出格式

样例输入

1 2 3 4 5

样例输出

4

题解

已知两只青蛙的初始位置和每一步跳的距离，求两只青蛙跳到同一点的最短时间，设最小时间为t，可得：

(x+m*t)-(y+n*t)=p*L

这个式子是个二元一次方程，而我们学过用扩展欧几里德求二元一次方程的解，其中二元一次方程的形式为

a*x+b*y=c

把上面的式子转化成相似形式可得

(n-m)*t+L*p=x-y  (*)

令：a=n-m, b=L, c=gcd(a,b), d=x-y

得：a*t+b*p=d  (1)

那么我们可以用扩展欧几里德求出一组t₀，p₀，使得

a*t₀+b*p₀=c  (2)

(1)式两边同除c得：a*t/c+b*p/c=d/c

易知a*t/c和b*p/c是整数，所以d/c也是整数，否则无解。

(2)式两边同乘(d/c)得：a*t₀*(d/c)+b*p₀*(d/c)=d

所以t₀*(d/c)为最小的解，但有可能为负数，为使最终答案为正，解为

(t₀*(d/c)%(b/c)+(b/c))%(b/c)

本题有个陷阱，两只青蛙谁在前谁在后是不确定的，但我们可以通过调整使第一只青蛙在前。

 

 

#include <cstdio>
#define ll long long
ll exgcd(ll a,ll b,ll &x,ll &y)
{
    if (!b)
    {
        x=1,y=0;
        return a;
    }
    ll ans=exgcd(b,a%b,x,y),t;
    t=x,x=y,y=t-a/b*y;
    return ans;
}
int main()
{
    ll gcd,X,Y,x,y,m,n,l,a,b,c,t;
    scanf("%lld%lld%lld%lld%lld",&x,&y,&m,&n,&l);
    a=n-m,c=x-y;
    if (a<0) a=-a,c=-c;
    gcd=exgcd(a,l,X,Y);  b=l/gcd;
    if (c%gcd) printf("Impossible");
    else printf("%lld",(c/gcd*X%b+b)%b);
    return 0;
}