【洛谷P1290】欧几里德的游戏

问题描述

输入格式

输出格式

样例输入

2
25 7
24 15

样例输出

Stan wins
Ollie wins

数据范围

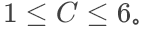
题解

先假设m为两个数中较大的数，n为较小的数。

考虑两种情况：

1、m div n =1,这种情况只有一种操作，即减去较小的数的一倍

2、m div n >1,这种情况有多种操作，即可以减去较小的数的一倍，两倍，三倍,……并且可以控制操作后是m>n还是n>m

对于第一种情况，这种情况下只有一种操作，是被动的，假设第i局到第j局都是第一种情况，第i-1局和第j+1局是第二种情况，那么只要知道第i局两个数的值，就一定可以推出第j+1局两个数的值。而第i局的值是由第i-1局决定的，所以第i-1局的操作者（设为甲，另一人为乙）是主动的。甲可以通过操作决定第j+1局的值，以及j-i+1的值。若j-i+1为奇数，即连续奇数局是第一种情况，则第j+1局的操作者又是甲，即甲将会再一次获得主动，反之乙会获得主动。由于两人“完美地操作”，甲可以通过操作后使m>n或n>m来控制下一次的主动落在自己手中。所以甲是必胜的，即先达到第二种情况的人必胜。

由题Stan先操作，若开始时是第二种情况，则Stan获胜，若开始时是第一种情况，就模拟找出第一个达到第二种情况的人为胜者。

 

#include <cstdio>
int c,m,n,f;
int main()
{
    int t;
    scanf("%d",&c);
    while (c--)
    {
        scanf("%d%d",&n,&m);
        if (n>m) t=m,m=n,n=t;
        f=1;
        while (m/n==1 && m%n)
          t=m%n,m=n,n=t,
          f^=1;
        if (f) printf("Stan wins\n");
        else printf("Ollie wins\n");
    }
    return 0;
}