算法设计与分析作业

作业要求：需要文字的部分手写拍照截图；算法要求程序代码完整；运行结果正确。提交PDF格式的电子文件。

第一章算法初步

第一章算法初步

题目 1 2 3 总分
分数

第1题，第3题，第4题

T1

  1. \(n\)、\(a\)变量为已知输入，\(x\)变量已被定义，请计算每段代码的时间复杂度。

(1)

for i in range(n):
    x += 1

整体时间复杂度是线性的

\(O(N)\)

(2)

for i in range(n):
    for j in range(n):
        x += 1

外循环执行n次，内循环也执行n次
\(O(N^2)\)

(3)

for i in range(n):
    for j in range(i):
        x += 1

外循环执行n次。对于每个i，内循环执行i次。

\(O(n(n-1)/2)\) 化简(只要最大的影响）：\(O(n^2)\)

(4)

for i in range(n):
    for j in range(i * i):
        x += 1

总的迭代次数是\(1^2 + 2^2 + 3^2 + ... + n^2\)。

\[\sum_{i=0}^{n-1} i^2 = 0^2 + 1^2 + 2^2 + \dots + (n-1)^2 \]

答案：

\[\frac{n(n-1)(2n-1)}{6} \]

所以是：\(O(n^3)\)

(5)

def power_recur(n, a):
    if a > 0:
        return n * power_recur(n, a - 1)
    else:
        return 1

每次递归都将参数\(a\)减少\(1\)，直到它变为\(0\)。因此，函数被调用了\(a + 1\)次（包括最初的调用）

\(O(a)\)

T3

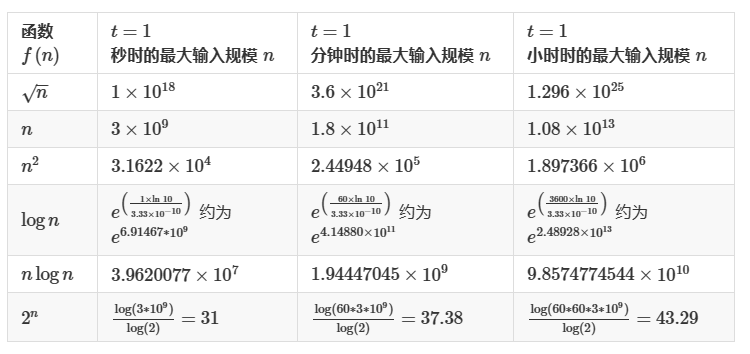
3.假设每一个求解问题的算法需要\(f(n)\)毫秒，已知函数\(f(n)\)和时间\(t\)，确定在时间可以求解的问题的最大输人规模\(n\)。已知条件及需要填写的参数如表 1-2 所示。

表 1-2

函数 \(f(n)\) \(t=1\) 秒时的最大输入规模 \(n\) \(t=1\) 分钟时的最大输入规模 \(n\) \(t=1\) 小时时的最大输入规模 \(n\)
\(\sqrt{n}\)
\(n\)
\(n^2\)
\(\log{n}\)
\(n \log{n}\)
\(2^n\)

代码：

#include <stdio.h>
#include <time.h>
int main() {
    long long n = 1000000000; // 10亿次加法运算
    clock_t st = clock();
    int result = 0;
    for (int i=1;i<=n;++i){
      result++; // 执行加法运算
    }
    clock_t et=clock();
    double used=(double)(et - st)/CLOCKS_PER_SEC;
    double ops = n/used;
    printf("res:%d ",result);
    printf("在1秒内完成了 %.0f 次加法运算\n",ops);
    return 0;
}

测了测，差不多在i7-12700（ESXI虚拟化下）大概\(2800000000\) = \(2.8*10^9\)

为了计算方便，认为下一代计算机CPU单核可以每秒\(3*10^9\)

➜  t1 cd "/home/dayi/code_/homework/t1/" && gcc cnt.c -o cnt && "/home/dayi/code_/homework/t1/"cnt
在1秒内完成了 2815347020 次加法运算
➜  t1 cd "/home/dayi/code_/homework/t1"
➜  t1 cd "/home/dayi/code_/homework/t1/" && gcc cnt.c -o cnt && "/home/dayi/code_/homework/t1/"cnt
在1秒内完成了 2821885415 次加法运算
➜  t1 cd "/home/dayi/code_/homework/t1"
➜  t1 cd "/home/dayi/code_/homework/t1/" && gcc cnt.c -o cnt && "/home/dayi/code_/homework/t1/"cnt
在1秒内完成了 2826399704 次加法运算
➜  t1 cd "/home/dayi/code_/homework/t1"
➜  t1 cd "/home/dayi/code_/homework/t1/" && gcc cnt.c -o cnt && "/home/dayi/code_/homework/t1/"cnt
在1秒内完成了 2862950557 次加法运算
➜  t1 
➜  t1

另外，浮点真的很慢，这样写的代码超级慢，也就跑600万左右。

#include <stdio.h>
#include <time.h>

int main() {
    long long n = 1000000000; // 10亿次加法运算
    clock_t st = clock();
    long long cnt = 0;
    for(;;){
      ++cnt;
      clock_t et=clock();
      if((float)(et-st)/CLOCKS_PER_SEC>=0.999){
        break;
      }
    }
    printf("在1秒内完成了 %.0lld 次加法运算\n",cnt);
    return 0;
}


➜  t1 clang++ cnt2.c -O3 -o ./cnt2_O3
clang: warning: treating 'c' input as 'c++' when in C++ mode, this behavior is deprecated [-Wdeprecated]
cnt2.c:15:57: warning: format specifies type 'int' but the argument has type 'long long' [-Wformat]
    printf("在1秒内完成了 %.0d 次加法运算\n",cnt);
                          ~~~~               ^~~
                          %.0lld
1 warning generated.
➜  t1 clang++ cnt2.c -O3 -o ./cnt2_O3
clang: warning: treating 'c' input as 'c++' when in C++ mode, this behavior is deprecated [-Wdeprecated]
➜  t1 clang++ cnt2.c -O3 -o ./cnt2_O3
clang: warning: treating 'c' input as 'c++' when in C++ mode, this behavior is deprecated [-Wdeprecated]
➜  t1 clang++ cnt2.c -O3 -o ./cnt2_O3 && ./cnt2_O3 
clang: warning: treating 'c' input as 'c++' when in C++ mode, this behavior is deprecated [-Wdeprecated]
在1秒内完成了 6606256 次加法运算
➜  t1 clang++ cnt2.c -O3 -o ./cnt2_O3 && ./cnt2_O3
clang: warning: treating 'c' input as 'c++' when in C++ mode, this behavior is deprecated [-Wdeprecated]
在1秒内完成了 6554973 次加法运算
➜  t1 clang++ cnt2.c -O3 -o ./cnt2_O3 && ./cnt2_O3
clang: warning: treating 'c' input as 'c++' when in C++ mode, this behavior is deprecated [-Wdeprecated]
在1秒内完成了 6561932 次加法运算
➜  t1 clang++ cnt2.c -O3 -o ./cnt2_O3 && ./cnt2_O3
clang: warning: treating 'c' input as 'c++' when in C++ mode, this behavior is deprecated [-Wdeprecated]
在1秒内完成了 6470152 次加法运算
➜  t1 clang++ cnt2.c -O3 -o ./cnt2_O3 && ./cnt2_O3
clang: warning: treating 'c' input as 'c++' when in C++ mode, this behavior is deprecated [-Wdeprecated]
在1秒内完成了 6584688 次加法运算
➜  t1

按照f(n)，当时间t为1s时候，可以跑\(3*10^9\)计算：

logn

  1. 对于 \(t = 1\) 秒：

\[n = e^{\left( \frac{1 \times \ln{10}}{3.33 \times 10^{-10}} \right)} \]

约为=\(e^{6.91467 * 10^{9}}\)

  1. 对于 \(t = 60\) 秒（1分钟）：

\[n = e^{\left( \frac{60 \times \ln{10}}{3.33 \times 10^{-10}} \right)} \]

约为=\(e^{4.14880 × 10^{11}}\)

  1. 对于 \(t = 3600\) 秒（1小时）：

\[n = e^{\left( \frac{3600 \times \ln{10}}{3.33 \times 10^{-10}} \right)} \]

约为=\(e^{2.48928×10^{13}}\)

函数 \(f(n)\) \(t = 1\) 秒时的最大输入规模 \(n\) \(t = 1\) 分钟时的最大输入规模 \(n\) \(t = 1\) 小时时的最大输入规模 \(n\)
\(\sqrt{n}\) \(1 \times 10^{18}\) \(3.6 \times 10^{21}\) \(1.296 \times 10^{25}\)
\(n\) \(3 \times 10^9\) \(1.8 \times 10^{11}\) \(1.08 \times 10^{13}\)
\(n^2\) \(3.1622 \times 10^4\) \(2.44948 \times 10^5\) \(1.897366 \times 10^6\)
\(\log{n}\) \(e^{\left( \frac{1 \times \ln{10}}{3.33 \times 10^{-10}} \right)}\) 约为 \(e^{6.91467 * 10^{9}}\) \(e^{\left( \frac{60 \times \ln{10}}{3.33 \times 10^{-10}} \right)}\) 约为 \(e^{4.14880 × 10^{11}}\) \(e^{\left( \frac{3600 \times \ln{10}}{3.33 \times 10^{-10}} \right)}\) 约为 \(e^{2.48928×10^{13}}\)
\(n \log{n}\) \(3.9620077 \times 10^7\) \(1.94447045 \times 10^9\) \(9.8574774544 \times 10^{10}\)
\(2^n\) \(\frac{\log(3*10^9)}{\log(2)}=31\) \(\frac{\log(60*3*10^9)}{\log(2)}=37.38\) \(\frac{\log(60*60*3*10^9)}{\log(2)}=43.29\)

防止公式解析失败

这个超好用

T4

  • 问题：举一个在生活中算法的例子，详细谈谈其是怎么提高效率的。

  • 快排，哈希表，索引Mysql在千万账户里二分找到我的账户，然后快速反馈给我余额，可以快速知道我的银行卡有没有清零。

开车去一个陌生的城市，并且需要找到最快的路线，以尽量少花费时间和资源。搜最短路，每个边的权值可以根据油耗，吃的，喝的等等来考虑~

第二章排序算法

第二章排序算法

题目 1 2 3 总分
分数

第2题，第4题，第5题

1. 给定n个数，并按从小到大的顺序，以列表的形式输出这n个数中前m小的数。

  • 输入格式：第一行输入两个数n和m，第二行输入n个数。
  • 输出格式：输出一个列表。
  • 保证数据范围 \(1≤m≤n≤10^6\)。

范例输入：

6 3
5 10 3 1 9 8

范例输出：

[1, 3, 5]

就是排序啦

代码

n,m=map(int,input().split())
ls = map(int,input().split())
ls = sorted(ls)
print(ls[0:-m])

运行结果

➜  t2 python -u "/home/dayi/code_/homework/t2/1.py"
6 3
5 10 3 1 9 8
[1, 3, 5]
➜  t2

2. 给定n个数，不断输入m并输出这n个数中第m大的数。当最新输入的m为0时，程序结束。

  • 保证数据范围 \(1≤m≤n≤10^6\)。
  • 输入格式：第一行输入一个数n，第二行输入n个数。接下来的每一行都输入m。
  • 输出格式：对于每一行的m，在单独一行输出列表中第m大的数。

范例输入：

7
3 14 90 78 32 43 61
1
4
6
0

范例输出：

90
43
14

排序之后，算一算位置，直接输出即可。

代码

n = int(input())
ls = list(map(int,input().split()))
ls.sort()
while True:
  m = eval(input())
  if m==0:
    break
  print(ls[-m])

运行结果

➜  t2 python -u "/home/dayi/code_/homework/t2/2.py"
7
3 14 90 78 32 43 61
1
4
6
090
43
14

➜  t2

3. 给定n个数，对这串数据进行排序后输出。（使用本章讲到的所有排序算法）

  • 保证数据范围 \(1≤m≤n≤10^6\)。
  • 输入格式：第一行输入一个数n，第二行输入n个数。
  • 输出格式：输出一个元素从小到大排列的列表。

还是排序www

范例输入：

4
5 1 2 4

范例输出：

[1 2 4 5]

代码

n = eval(input())
ls = list(map(int,input().split()))
ls.sort()
print("".join(str(i)+" " for i in ls))

运行结果

➜  t2 cd "/home/dayi/code_/homework/t2"
➜  t2 python -u "/home/dayi/code_/homework/t2/3.py"
4
5 1 2 4
1 2 4 5 
➜  t2

4. 给定一组n·m排列的数，每个数都有一个坐标（x,y），表示这个数在第x行第y列。通过输入在第a行和第b列组成的十字中，用1～k来表示这其中的每一个数，使得它们之间的大小关系一个坐标（a，b）来指定一个数进行下列操作。

  • 与更改前保持一致。其中，给第a行和第b列中最小的元素赋值为1，最大的元素赋值为k。输出使坐标（a,b）的元素符合这种规律的最小值。
  • 保证数据范围 \(1≤m，n≤10^3\)。坐标从1开始，a和b皆为正整数，\(a≤n，b≤m\)。
  • 输入格式：第一行输入两个数n和m，第2至n＋1行每行输入m个数，第n＋2行输入两个数a和b。
  • 输出格式：输出最小值min。

范例输入：

3 4
3 1 9 4
2 5 1 7
8 6 5 2
2 2

范例输出：

3

思路：

  • 从矩阵中提取出第 a 行和第 b 列的所有元素。

  • 对这些元素去重。然后，对这些唯一的元素进行排序。

  • 建立映射：为了 (a, b) 处元素的最小值，为十字区域每个唯一元素建立一个从元素值到它的“新”值（1 到 k）的映射。

  • 使用这个映射，我们找出坐标 (a, b) 处的元素在排序后的新排列中对应的值，即答案

代码：

def min_val(n, m, mat, a, b):
    cross = set(mat[a-1] + [row[b-1] for row in mat])
    sorted_cross = sorted(list(cross))
    mapping = {elem: i+1 for i, elem in enumerate(sorted_cross)}
    return mapping[mat[a-1][b-1]]

# 样例
n, m = 3,4
mat = [
    [3, 1, 9, 4],
    [2, 5, 1, 7],
    [8, 6, 5, 2]
]
a, b = 2,2
res = min_val(n, m, mat, a, b)
print(res)

运行结果

➜  t2 python -u "/home/dayi/code_/homework/t2/4.py"
3
➜  t2

4.9 归并+快排

快速排序

n = int(input())
ls = list(map(int, input().split()))
def sort(l, r):
    if l >= r:
        return
    i = l - 1
    j = r + 1
    import random
    val = ls[random.randint(l,r)]
    while i < j:
        i += 1
        while i < r and ls[i] < val:
            i += 1
        j -= 1
        while j > l and ls[j] > val:
            j -= 1
        if i < j:
            ls[i], ls[j] = ls[j], ls[i]
    sort(l, j)
    sort(j + 1, r)
sort(0, len(ls) - 1)
print(" ".join(str(i) for i in ls))

归并排序

n = int(input())
ls = list(map(int, input().split()))
def merge_sort(l,r):
  if l>=r:
    return
  mid = (l+r)//2
  merge_sort(l,mid)
  merge_sort(mid+1,r)
  i,j = l,mid+1
  tmp = []
  while i<=mid and j<=r and i<=j:
    if ls[i]<ls[j]:
      tmp.append(ls[i])
      i+=1
    else:
      tmp.append(ls[j])
      j+=1
  while j<=r:
    tmp.append(ls[j])
    j+=1
  while i<=mid:
    tmp.append(ls[i])
    i+=1
  for i in range(l, r + 1):
    # 注意
    ls[i] = tmp[i - l]

merge_sort(0, len(ls) - 1)
print(" ".join(str(i) for i in ls))

5.给定n个数，求这串数据中存在多少个逆序对。（逆序对的定义：对于列表中的任意两个数而言，如果排在前面的数大于排在后面的数，则它们构成一个逆序对。）

题目描述：
给定n个数，求这串数据中存在多少个逆序对。（逆序对的定义：对于列表中的任意两个数而言，如果排在前面的数大于排在后面的数，则它们构成一个逆序对。）

保证数据范围\(1 ≤ n ≤ 10^5\)。提示：使用归并排序。

输入格式：

第一行输入一个数n，第二行输入n个数。

输出格式：

输出逆序对的总数x。

示例输入：

5
3 1 9 4 2

示例输出：

5

解题思路

  1. 归并排序：在归并排序的合并步骤中，当我们从两个子数组中选择较小的元素时，更新逆序对的计数。

  2. 计算逆序对：在合并两个已排序的子数组时，如果左侧子数组的当前元素大于右侧子数组的当前元素，那么左侧子数组中当前元素及其之后的所有元素都将与右侧子数组的当前元素形成逆序对。

代码：

n = int(input())
ls = list(map(int, input().split()))

def merge_sort(l, r):
    if l >= r:
        return 0
    mid = (l + r) // 2
    count = merge_sort(l, mid) + merge_sort(mid + 1, r)
    i, j = l, mid + 1
    tmp = []

    while i <= mid and j <= r:
        if ls[i] <= ls[j]:
            tmp.append(ls[i])
            i += 1
        else:
            tmp.append(ls[j])
            count += mid - i + 1  # 计算逆序对
            j += 1

    while j <= r:
        tmp.append(ls[j])
        j += 1
    while i <= mid:
        tmp.append(ls[i])
        i += 1

    for i in range(l, r + 1):
        ls[i] = tmp[i - l]

    return count

count = merge_sort(0, len(ls) - 1)
print(count)

运行结果

➜  t2 python -u "/home/dayi/code_/homework/t2/5.py"
5
3 1 9 4 2
5
➜  t2

第三章查找

题目 1 2 3 总分
分数

第4题，第5题

写出折半查找的递归算法

第三章查找 T4 题目描述

4.按题目要求，建立一棵二叉搜索树。可以对二叉搜索树进行4种操作。

  • （1）插入元素x，格式为：\(I_x\)。
  • （2）删除元素x，格式为：\(D_x\)。
  • （3）查询元素x的前驱，格式为：\(P_x\)。
  • （4）查询元素x的后继，格式为：\(S_x\)。
    其中，x为一个正整数，x前面的字母代表进行了何种操作。进行两种查询操作后，如果元素存在于二叉搜索树中：
  • （1）如果元素有前驱/后继，输出它的前驱/后继；
  • （2）如果二叉搜索树中不存在它的前驱/后继，输出自己定义的正无穷/负无穷。
    如果元素不存在于二叉搜索树中，输出0。
    一共有n条操作，保证输入的所有操作均为合法操作。（当二叉搜索树为空时不会给出删除操作等，即不必对特殊情况进行判定。）
    输入格式：第一行输入一个数n，接下来n行每一行输入一个代表操作的字母和元素x，中间用空格隔开。
    输出格式：每次进行查询操作后输出结果；每次查询操作的输出结果单独占一行。
    保证数据范围：\(1≤n≤10^{5}\)。
    示例输入：
8
I 1
I 4
I 5
P 4
P 5
I 3
D 4
P 5
S 6

示例输出：

1
4
3
0

第三章查找 T4 题目分析

二叉搜索树。
数据结构写一下。

  1. 二叉搜索树的定义:

    • 定义了TreeNode 类，树的节点。节点包含一个值 val 以及指向左右子节点的指针。
    • BST 类代表整个二叉搜索树，具有一个根节点 root。

  2. 插入操作 (ins):

    • 插入新值时，如果当前节点为空，则直接在该位置创建新节点。
    • 如果插入的值小于当前节点的值，递归地在左子树插入；如果大于，则在右子树插入。

  3. 删除操作 (del_):

    • 如果要删除的值小于或大于当前节点的值，递归地在左子树或右子树中删除。
    • 如果找到要删除的值，有几种情况处理：
      • 如果节点只有一个子节点或没有子节点，直接用其子节点（如果有）替换它。
      • 如果节点有两个子节点，则找到右子树中的最小节点（后继），用它的值替换当前节点的值，并在右子树中删除该后继节点。

  4. 查找前驱 (pred):

    • 遍历树寻找前驱，如果当前节点的值小于给定值，则可能是前驱，更新前驱值，并向右子树继续查找；否则向左子树查找。

  5. 查找后继 (succ):

    • 同样，遍历树寻找后继，如果当前节点的值大于给定值，则可能是后继，更新后继值，并向左子树继续查找；否则向右子树查找。

  6. 处理OPT:

    • 根据输入的opt（"I"、"D"、"P"、"S"）分别执行插入、删除、查找前驱、查找后继的操作。

  7. 输出:

    • 输出查询操作的结果。如果查询的元素不存在于树中，根据前驱或后继的定义输出相应的正无穷或负无穷值；如果查询的元素存在于树中但没有前驱或后继，输出0。

第三章查找 T4 代码

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class BST:
    def __init__(self):
        self.root = None

    def ins(self, val):
        self.root = self._ins(self.root, val)

    def _ins(self, node, val):
        if not node:
            return TreeNode(val)
        if val < node.val:
            node.left = self._ins(node.left, val)
        elif val > node.val:
            node.right = self._ins(node.right, val)
        return node

    def del_(self, val):
        self.root = self._del_(self.root, val)

    def _del_(self, node, val):
        if not node:
            return None
        if val < node.val:
            node.left = self._del_(node.left, val)
        elif val > node.val:
            node.right = self._del_(node.right, val)
        else:
            if not node.left:
                return node.right
            elif not node.right:
                return node.left
            min_larger_node = self._get_min(node.right)
            node.val = min_larger_node.val
            node.right = self._del_(node.right, min_larger_node.val)
        return node

    def _get_min(self, node):
        while node.left:
            node = node.left
        return node

    def pred(self, val):
        node = self.root
        pred = float("inf")
        while node:
            if node.val < val:
                pred = node.val
                node = node.right
            else:
                node = node.left
        return pred if pred != float("inf") else 0

    def succ(self, val):
        node = self.root
        succ = float("-inf")
        while node:
            if node.val > val:
                succ = node.val
                node = node.left
            else:
                node = node.right
        return succ if succ != float("-inf") else 0


bst = BST()
ops = [
    ("I", 1),
    ("I", 4),
    ("I", 5),
    ("P", 4),
    ("P", 5),
    ("I", 3),
    ("D", 4),
    ("P", 5),
    ("S", 6),
]

output = []
for op, x in ops:
    if op == "I":
        bst.ins(x)
    elif op == "D":
        bst.del_(x)
    elif op == "P":
        output.append(bst.pred(x))
    elif op == "S":
        output.append(bst.succ(x))

print(output)

第三章查找 T4 运行结果：

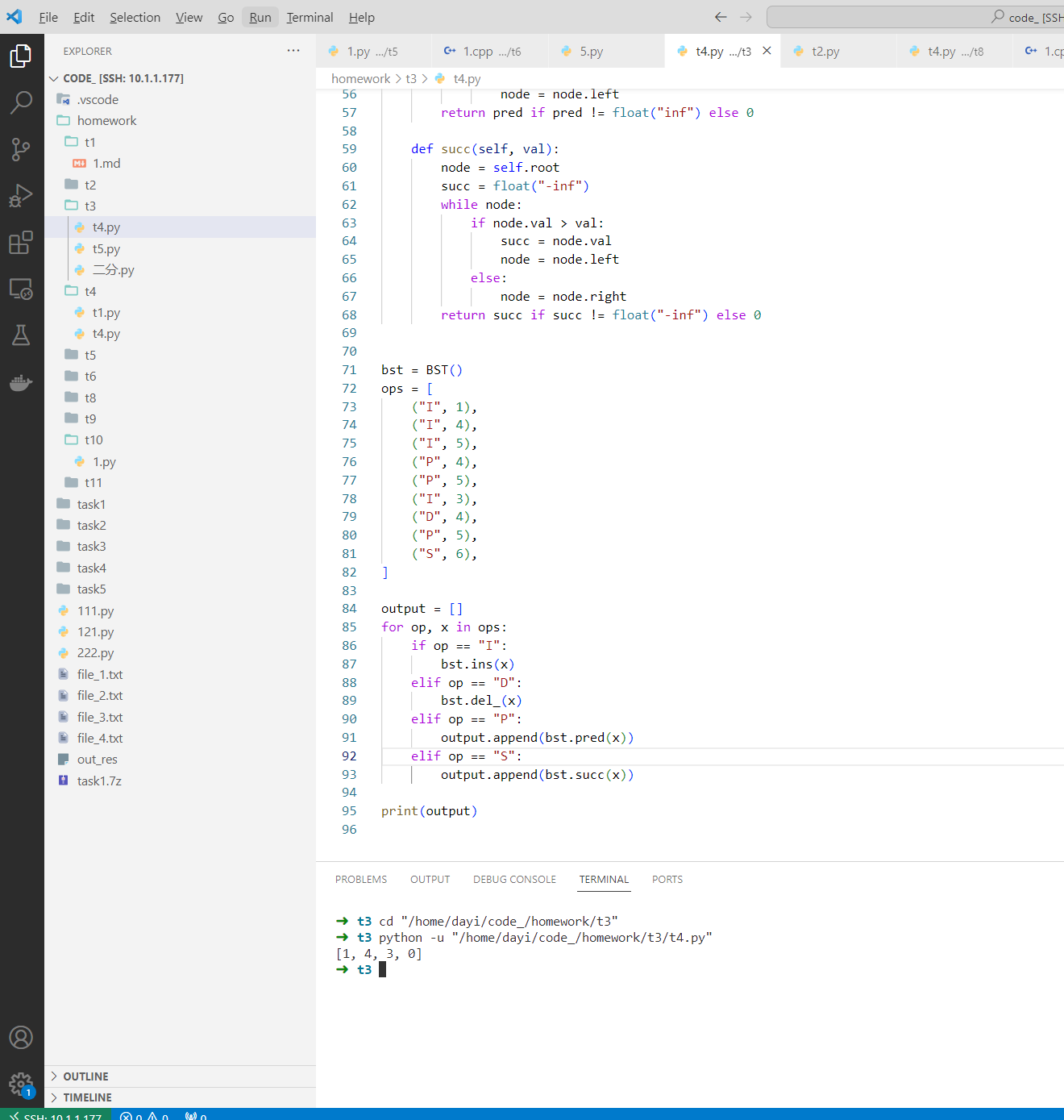
➜  t3 python -u "/home/dayi/code_/homework/t3/t4.py"
[1, 4, 3, 0]
➜  t3

第三章查找 T5

第三章查找 T5 题目描述

5.已知有n个数，将它们按输入顺序依次插入进一棵二叉平衡树中。请问这棵平衡树的深度是多少？

  • 输入格式：第一行输入一个数\(n\)，第二行输入\(n\)个正整数，每个数之间用空格隔开。

  • 输出格式：输出一个表示深度的正整数。

  • 保证数据范围\(1 \leq n \leq 10^5\)。

样例输入：

8
1 5 4 2 3 7 6 9

样例输出：

4

第三章查找 T5 题目分析

这题不会写，参考了网上的一些内容。

  1. AVL树节点:

    • AVLTreeNode 类定义了一个AVL树的节点，包括节点的值 val、高度 height 以及左右子节点的引用。

  2. AVL树的插入操作:

    • 插入新节点时，按照二叉搜索树的规则插入。
    • 插入后更新节点的高度，并检查该节点的平衡因子（左子树高度减去右子树高度）。如果平衡因子的绝对值大于1，则进行相应的旋转操作以恢复平衡。

  3. 旋转操作:

    • 左旋、右旋、左右旋和右左旋，以处理不同的不平衡情况。
    • 每次插入后，树可能会进行一次或多次旋转操作以保持平衡。

  4. 计算树的深度:

    • 通过计算根节点的高度来得到整棵树的深度。

第三章查找 T5 代码

class AVLTreeNode:
    def __init__(self, val=0, height=1, left=None, right=None):
        self.val = val
        self.height = height
        self.left = left
        self.right = right

class AVLTree:
    def __init__(self):
        self.root = None

    def insert(self, val):
        self.root = self._insert(self.root, val)

    def _insert(self, node, val):
        if not node:
            return AVLTreeNode(val)
        if val < node.val:
            node.left = self._insert(node.left, val)
        else:
            node.right = self._insert(node.right, val)

        node.height = 1 + max(self._get_height(node.left), self._get_height(node.right))
        balance = self._get_balance(node)

        if balance > 1 and val < node.left.val:
            return self._right_rotate(node)
        if balance < -1 and val > node.right.val:
            return self._left_rotate(node)
        if balance > 1 and val > node.left.val:
            node.left = self._left_rotate(node.left)
            return self._right_rotate(node)
        if balance < -1 and val < node.right.val:
            node.right = self._right_rotate(node.right)
            return self._left_rotate(node)

        return node

    def _left_rotate(self, z):
        y = z.right
        T2 = y.left

        y.left = z
        z.right = T2

        z.height = 1 + max(self._get_height(z.left), self._get_height(z.right))
        y.height = 1 + max(self._get_height(y.left), self._get_height(y.right))

        return y

    def _right_rotate(self, y):
        x = y.left
        T2 = x.right

        x.right = y
        y.left = T2

        y.height = 1 + max(self._get_height(y.left), self._get_height(y.right))
        x.height = 1 + max(self._get_height(x.left), self._get_height(x.right))

        return x

    def _get_height(self, node):
        if not node:
            return 0
        return node.height

    def _get_balance(self, node):
        if not node:
            return 0
        return self._get_height(node.left) - self._get_height(node.right)

    def get_depth(self):
        return self._get_height(self.root)

# 测试样例
avl_tree = AVLTree()
numbers = [1, 5, 4, 2, 3, 7, 6, 9]
for num in numbers:
    avl_tree.insert(num)

print(avl_tree.get_depth())

第三章查找，T5 运行结果

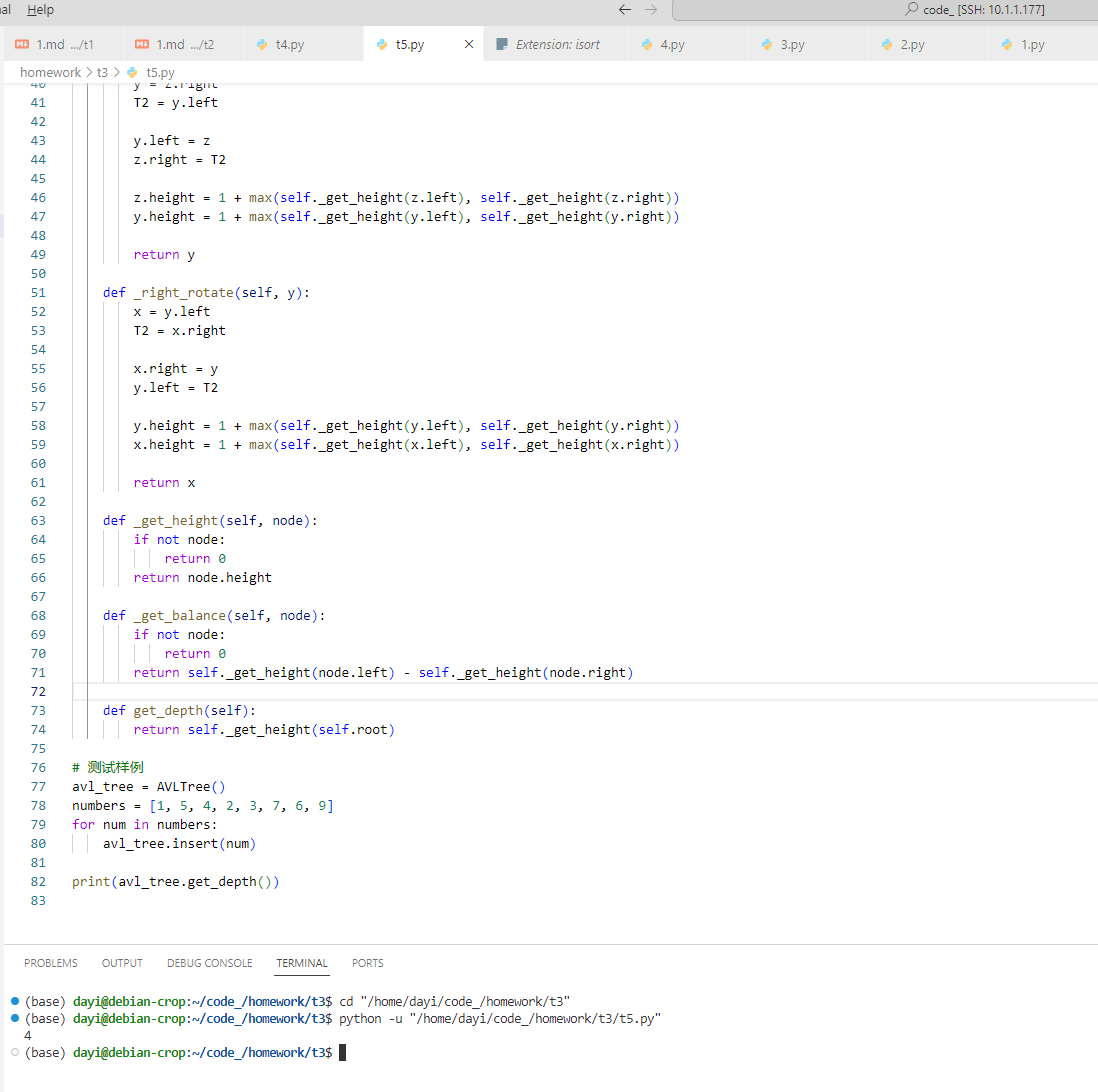
➜  t3 cd "/home/dayi/code_/homework/t3"
➜  t3 python -u "/home/dayi/code_/homework/t3/t5.py"
4
➜  t3

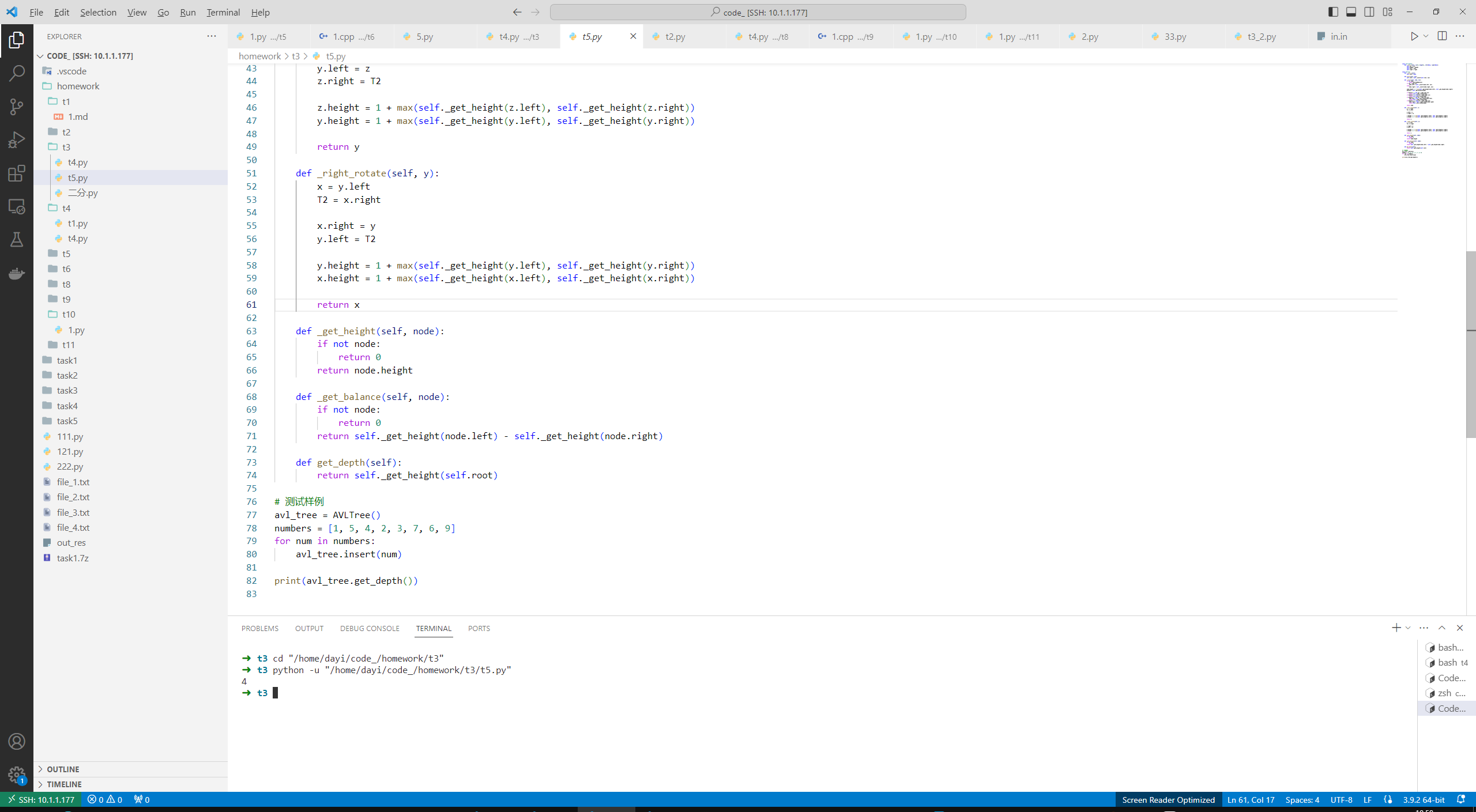
第三章查找 折半查找

# n,k = map(int,input().split())
# ls = list(map(int,input().split()))
n,k = 9,4
ls = [1, 2, 3, 4, 5, 6, 7, 8, 9]
ls.sort()
print(ls)
def find(l,r,x):
  if l>=r:
    return -1
  mid = (l+r)//2
  if ls[mid]==x:
    return mid
  elif ls[mid]>x:
    return find(l,mid,x)
  else:
    return find(mid+1,r,x)
print("index:",find(0,len(ls)-1,k))


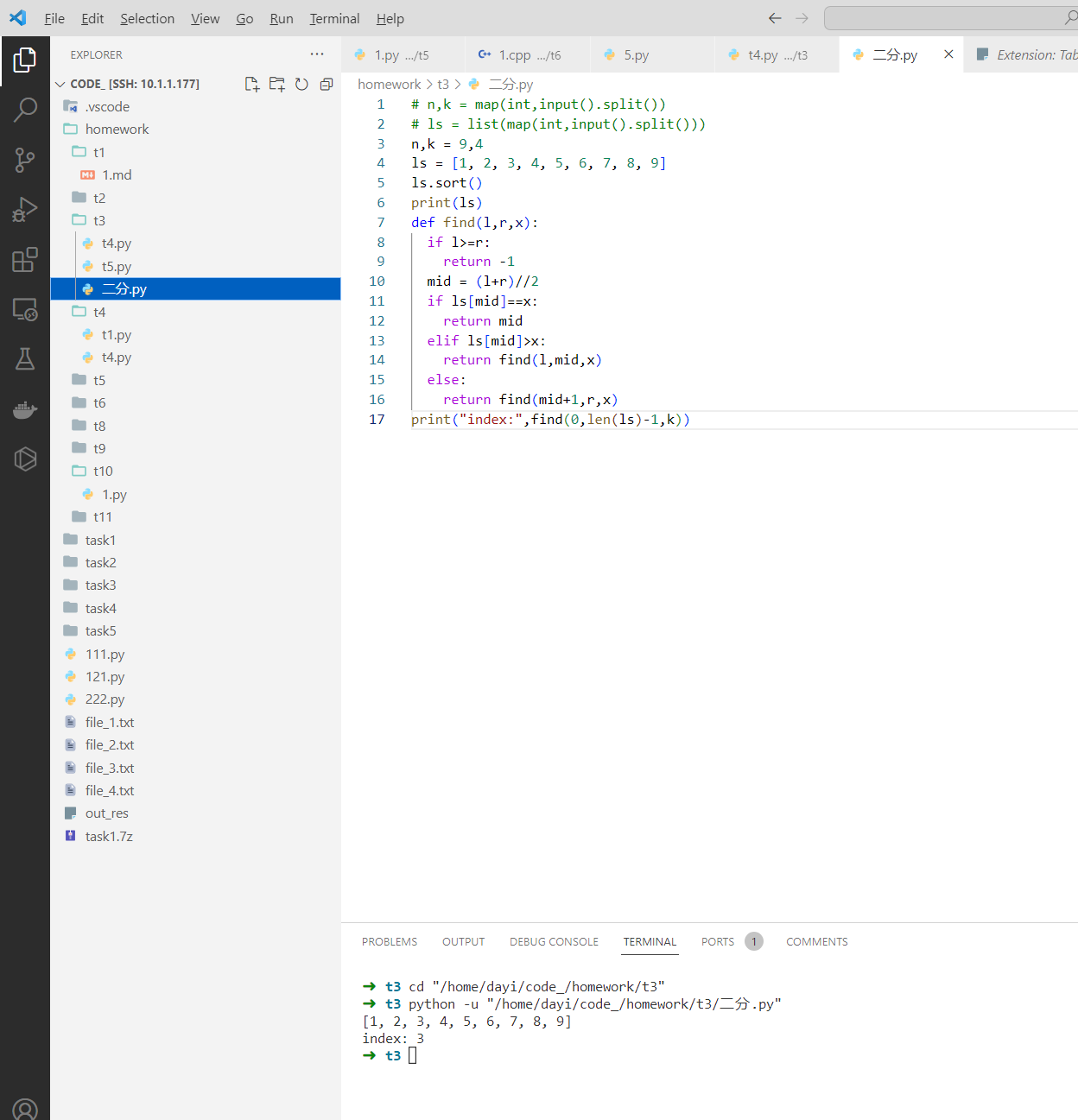
➜  t3 cd "/home/dayi/code_/homework/t3"
➜  t3 python -u "/home/dayi/code_/homework/t3/二分.py"
[1, 2, 3, 4, 5, 6, 7, 8, 9]
index: 3
➜  t3

第四章指针问题

第四章指针问题

题目 1 2 总分
分数

第1题，第4题

T1:题目：合并两个有序单链表，使得合并之后还是有序的

题目：合并两个有序单链表，使得合并之后还是有序的

class link_node:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

def create_list(list_):
    if not list_:
        return None
    head = link_node(list_[0])
    now = head
    for v in list_[1:]:
        now.next = link_node(v)
        now = now.next
    return head

def print_list(link_list):
    val = []
    current = link_list
    while current:
        val.append(current.val)
        current = current.next
    return val

def merge(l1, l2):
    dummy = link_node()
    tail = dummy
    while l1 and l2:
        if l1.val < l2.val:
            tail.next = l1
            l1 = l1.next
        else:
            tail.next = l2
            l2 = l2.next
        tail = tail.next
    if l1:
        tail.next = l1
    elif l2:
        tail.next = l2
    return dummy.next

ls1 = create_list([1, 3, 5, 7])
ls2 = create_list([2, 5, 8, 9])
print(print_list(merge(ls1, ls2)))

img

➜  t4 python -u "/home/dayi/code_/homework/t4/t1.py"
[1, 2, 3, 5, 5, 7, 8, 9]
➜  t4

T4:题目：给定一个数组，里面有奇数和偶数，使得左边都是奇数，右边都是偶数

题目：给定一个数组，里面有奇数和偶数，使得左边都是奇数，右边都是偶数

一个从数组的开始向前移动，另一个从数组的末尾向后移动。

当左边的指针指向偶数而右边的指针指向奇数时，我们交换这两个元素的位置。

def ord_arr(arr):
    # 双指针
    # 左边的都是奇数，右边的都是偶数
    left, right = 0, len(arr) - 1
    while left < right:
        while left < right and arr[left] % 2 == 1:
            left += 1
        while left < right and arr[right] % 2 == 0:
            right -= 1
        if left < right:
            arr[left], arr[right] = arr[right], arr[left]
    return arr

arr = [1, 1, 4, 5, 1, 4, 19, 19, 23, 53, 34, 34, 324, 43]
print(ord_arr(arr))

img

➜  t4 cd "/home/dayi/code_/homework/t4"
➜  t4 python -u "/home/dayi/code_/homework/t4/t4.py"
[1, 1, 43, 5, 1, 4, 19, 19, 23, 53, 34, 34, 324, 4]
➜  t4

第五章哈希算法

第五章哈希算法

题目 1 总分
分数

第1题

第五章哈希算法T1题目描述

设计一个辅助输入程序，在日常打字中，常常会打错，如把“the”打为“teh”，设计一个方法 respell()，以输入一句话作为参数，需要根据纠错表来把错词修改为正确的词语并返回结果。例如，纠错表 respellings 如下：

spellings = {
    "teh": "the",
    "lite": "light",
    "lol": "haha",
    "ting": "thing"
}

调用 respell("I ate teh whole ting.") 函数后结果如下： "I ate the whole thing."

第五章哈希算法T1题目解析

通过一个函数 respell 实现，该函数接受一句话作为参数，并根据预定义的纠错表（一个字典）来识别和修正错误的单词。

纠错表包含了一系列常见的拼写错误及其正确的拼写形式。

具体来说：

  1. 函数设计：respell 函数接受一个字符串（句子）作为输入。
  2. 纠错表：使用一个字典（spellings），其中键是错误的拼写，值是正确的拼写。例如，"teh": "the" 表示将 "teh" 纠正为 "the"。
  3. 使用正则表达式进行替换：利用 Python 的 re（正则表达式）库来查找和替换文本中的错误单词。这允许它在句子中准确地定位和替换单词，而不会错误地替换包含这些字母序列的较长单词。
  4. 灵活性和可扩展性：通过简单地向字典添加条目，可以轻松地扩展程序以纠正更多的拼写错误。

第五章哈希算法T1代码

import re

def respell(sen):
    spellings = {
        "teh": "the",
        "lite": "light",
        "lol": "haha",
        "ting": "thing",
        "adress": "address",
        "alot": "a lot",
        "athough": "although",
        "becuase": "because",
        "definately": "definitely",
        "goverment": "government",
        "grat": "great",
        "happend": "happened",
        "insted": "instead",
        "knowlege": "knowledge",
        "libary": "library",
        "occurance": "occurrence",
        "oppurtunity": "opportunity",
        "proffesor": "professor",
        "recieve": "receive",
        "seperate": "separate",
        "similer": "similar",
        "succesful": "successful",
        "suprise": "surprise",
        "tommorow": "tomorrow",
        "tounge": "tongue",
        "untill": "until",
        "wether": "whether",
        "wich": "which",
        "wierd": "weird",
        "yatch": "yacht",
        "youre": "you're"
    }
    
    for wrong, right in spellings.items():
        sen = re.sub(r'\b{}\b'.format(wrong), right, sen)
    
    return sen

sentence = "I ate teh whole ting."
re_sentence = respell(sentence)
print(re_sentence)

第五章哈希算法T1运行结果

img

第六章深度优先搜索算法

第5题

题目 1 总分
分数

第六章深度优先算法T5

题目描述

已知一个特殊的递归函数 f(a, b, c)，它根据以下规则返回一个整数值：

  1. 基础情况：

    • 如果 a ≤ 0 或 b ≤ 0 或 c ≤ 0，则函数返回 1。

    • 如果 a ≥ 20 或 b ≥ 20 或 c ≥ 20，则函数返回 f(20, 20, 20) 的值。

  2. 递归情况：

    • 如果 a < b 且 b < c，则函数返回

    equation1。

    • 在其他情况下，函数返回
      equation2。

题目解析

类似于动态规划的问题，其中函数的输出依赖于其较小输入值的输出。

函数通过多个递归分支逐步减小输入值，并在满足某些条件时返回基础值（如果 a ≤ 0 或 b ≤ 0 或 c ≤ 0，则函数返回 1）。

  • 函数的基础情况 确保在输入值较小或超过一定阈值时，函数能够直接返回一个简单的结果，从而避免无限递归。

  • 函数的递归情况 设计用于处理更复杂的输入。这些情况通过改变输入值来递归地调用自身，并根据特定的规则组合这些调用的结果。

由于这个函数涉及多个递归调用，计算复杂度较高，尤其是对于较大的输入值（例如 f(20,20,20)）。

因此，可以使用记忆化搜索来优化算法。

代码

vis={}
def f(a,b,c):
  # print(a,b,c)
  if (a, b, c) in vis:
    return vis[(a, b, c)]
  if a <= 0 or b <= 0 or c <= 0:
    return 1
  if a > 20 or b > 20 or c > 20:
    return f(20, 20, 20)
  if a < b and b < c:
    result=f(a,b,c-1)+f(a,b-1,c-1)-f(a,b-1,c)
  else:
    result=f(a-1,b,c)+f(a-1,b-1,c)+f(a-1,b,c-1)-f(a-1,b-1,c-1)
  vis[(a, b, c)] = result
  return result
import sys
sys.setrecursionlimit(1999999)
print(f(10,10,10))
print(f(20,20,20))

运行结果

➜  t6 cd "/home/dayi/code_/homework/t6"
➜  t6 python -u "/home/dayi/code_/homework/t6/5.py"
1024
1048576
➜  t6

img

第七章广度优先搜索算法

第七章广度优先搜索算法

题目 1 总分
分数

第2题

第七章广度优先搜索算法- P120 第2题

已知一个 N·M 的国际象棋棋盘，现给定一个起始点、终点。若在起始点上有一个马，
问：从起始点出发，马能否到达终点，到终点最少需要走几步？
输入中包含棋盘的大小、起始点坐标、终点坐标。（马走“日”字。）

这个 比较神奇，它可以走日字：

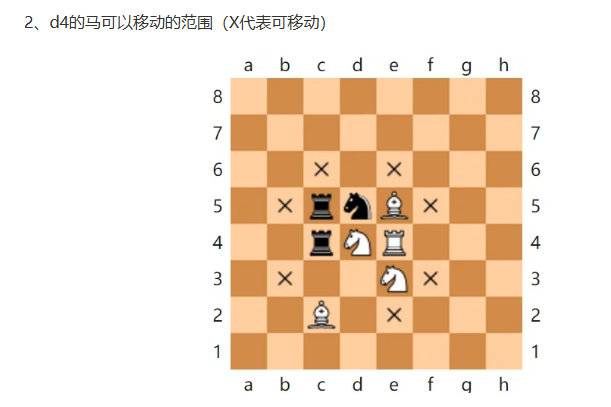
于是找到了个差不多的题目。

https://www.luogu.com.cn/problem/P1443

  • 因为求的是最少走多少步，我们在当前的状态里可以求得答案的话，那么下层状态求的一定是更多的数量。
  • 这个性质直接用 BFS 就可以啦

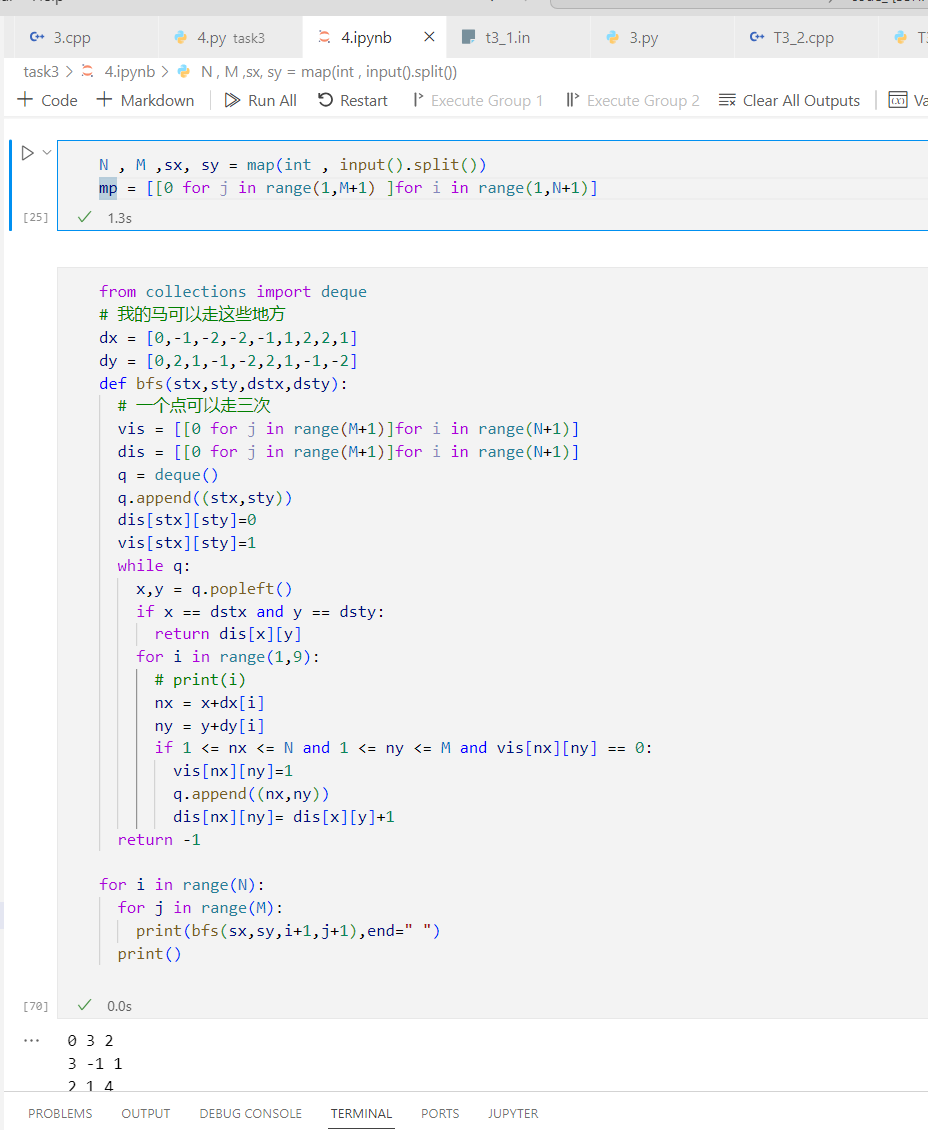
N , M ,sx, sy = map(int , input().split())
mp = [[0 for j in range(1,M+1) ]for i in range(1,N+1)]
from collections import deque
# 我的马可以走这些地方
dx = [0,-1,-2,-2,-1,1,2,2,1]
dy = [0,2,1,-1,-2,2,1,-1,-2]
def bfs(stx,sty,dstx,dsty):
  # 一个点可以走三次
  vis = [[0 for j in range(M+1)]for i in range(N+1)]
  dis = [[0 for j in range(M+1)]for i in range(N+1)]
  q = deque()
  q.append((stx,sty))
  dis[stx][sty]=0
  vis[stx][sty]=1
  while q:
    x,y = q.popleft()
    if x == dstx and y == dsty:
      return dis[x][y]
    for i in range(1,9):
      # print(i)
      nx = x+dx[i]
      ny = y+dy[i]
      if 1 <= nx <= N and 1 <= ny <= M and vis[nx][ny] == 0:
        vis[nx][ny]=1
        q.append((nx,ny))
        dis[nx][ny]= dis[x][y]+1
  return -1

for i in range(N):
  for j in range(M):
    print(bfs(sx,sy,i+1,j+1),end=" ")
  print()

虽然没过，试一试 C++：

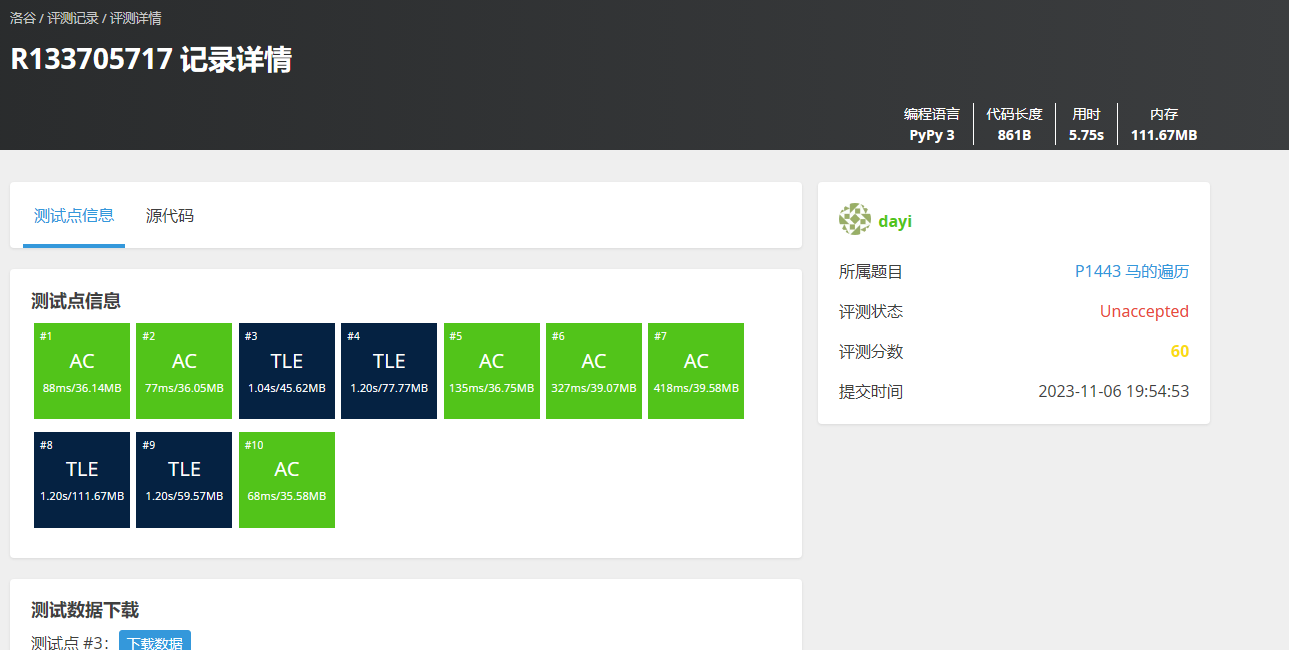
用c++试一试：

#include<bits/stdc++.h>

const int maxn = 2333;
const int maxm = 2333;
int dx[] = {0,-1,-2,-2,-1,1,2,2,1};
int dy[] = {0,2,1,-1,-2,2,1,-1,-2};
int N,M;
int vis[maxn][maxm];
int dis[maxn][maxm];
#define rep(i,x,y) for(int i=x;i<=y;++i)

inline void clear(){
  rep(i,1,N){
    rep(j,1,M){
      vis[i][j]=0;
      dis[i][j]=0;
    }
  }
}

inline int bfs(int stx,int sty,int dstx,int dsty){
  using namespace std;
  queue<pair<int, int>> q;
  clear();
  q.push({stx, sty});
  vis[stx][sty] = 1;
  while (!q.empty()) {
    int x = q.front().first;
    int y = q.front().second;
    q.pop();
    if(x==dstx&&y==dsty){
      return dis[dstx][dsty];
    }
    for(int i=1;i<=8;++i){
      int nx = x+dx[i];
      int ny = y+dy[i];
      if (nx >= 1 && nx <= N && ny >= 1 && ny <= M && vis[nx][ny] == 0) {
        vis[nx][ny] = 1;
        q.push({nx, ny});
        dis[nx][ny] = dis[x][y] + 1;
      }
    }
  }
  return -1;
}
int main(){
  int sx,sy;
  std::cin>>N>>M>>sx>>sy;
  rep(i,1,N){
    rep(j,1,M){
      std::cout<<bfs(sx,sy,i,j)<<" ";
    }
    std::cout<<"\n";
  }
}

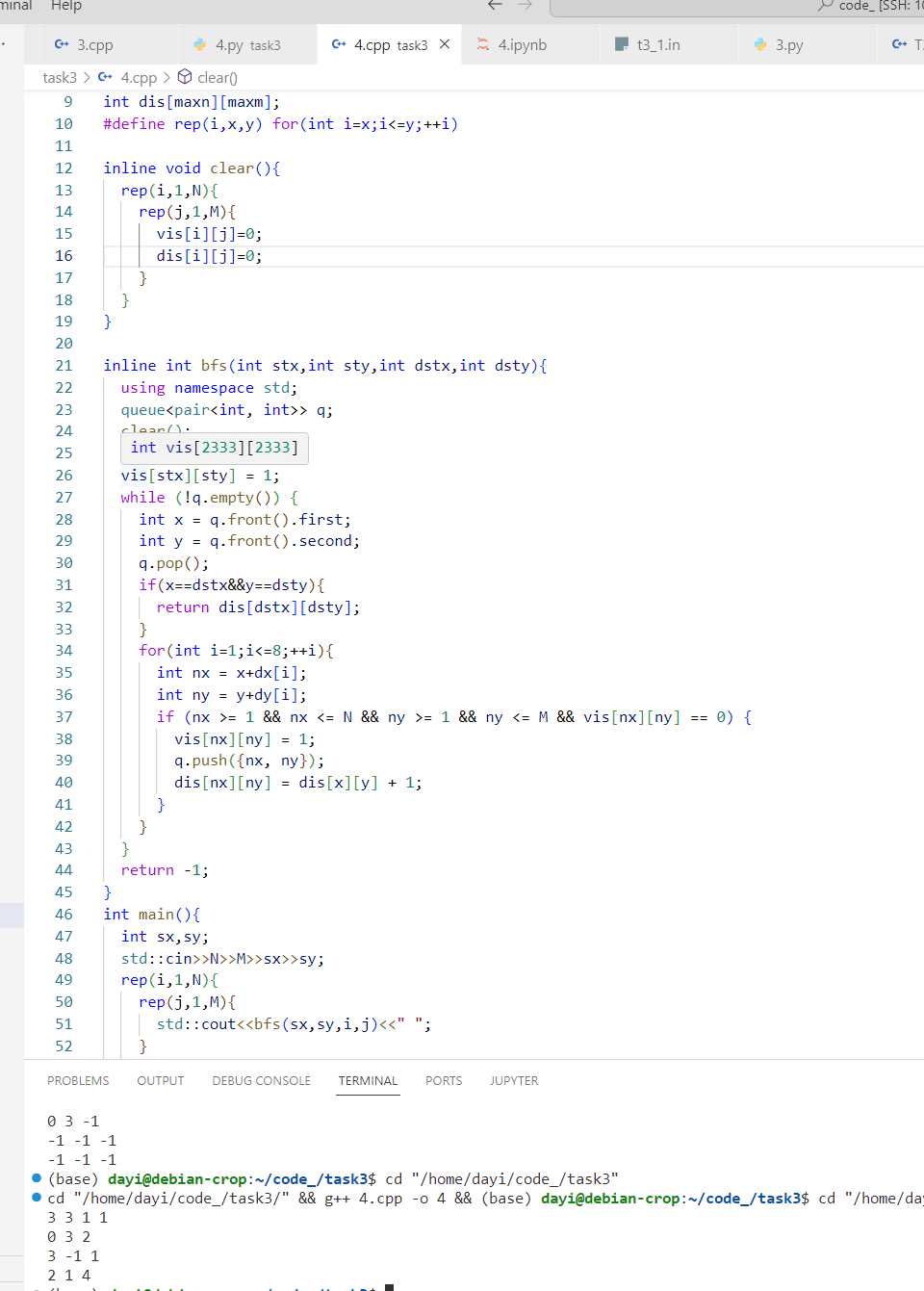
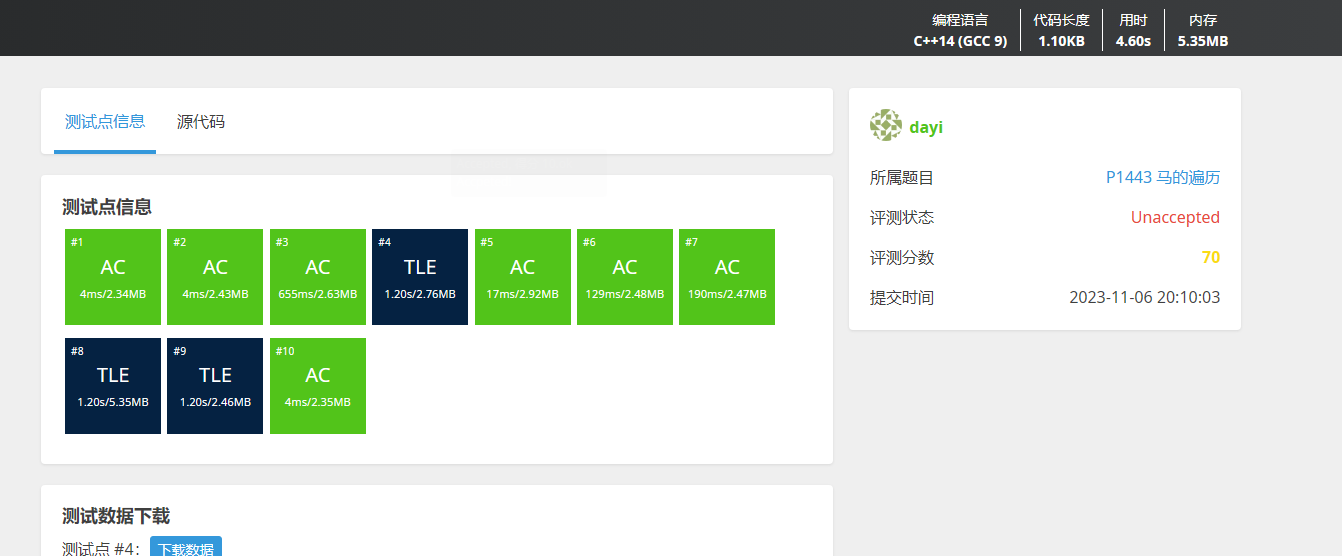
想了想，对于这个题，目标其实不变。所以不用 BFS 多次，BFS 一次就行：

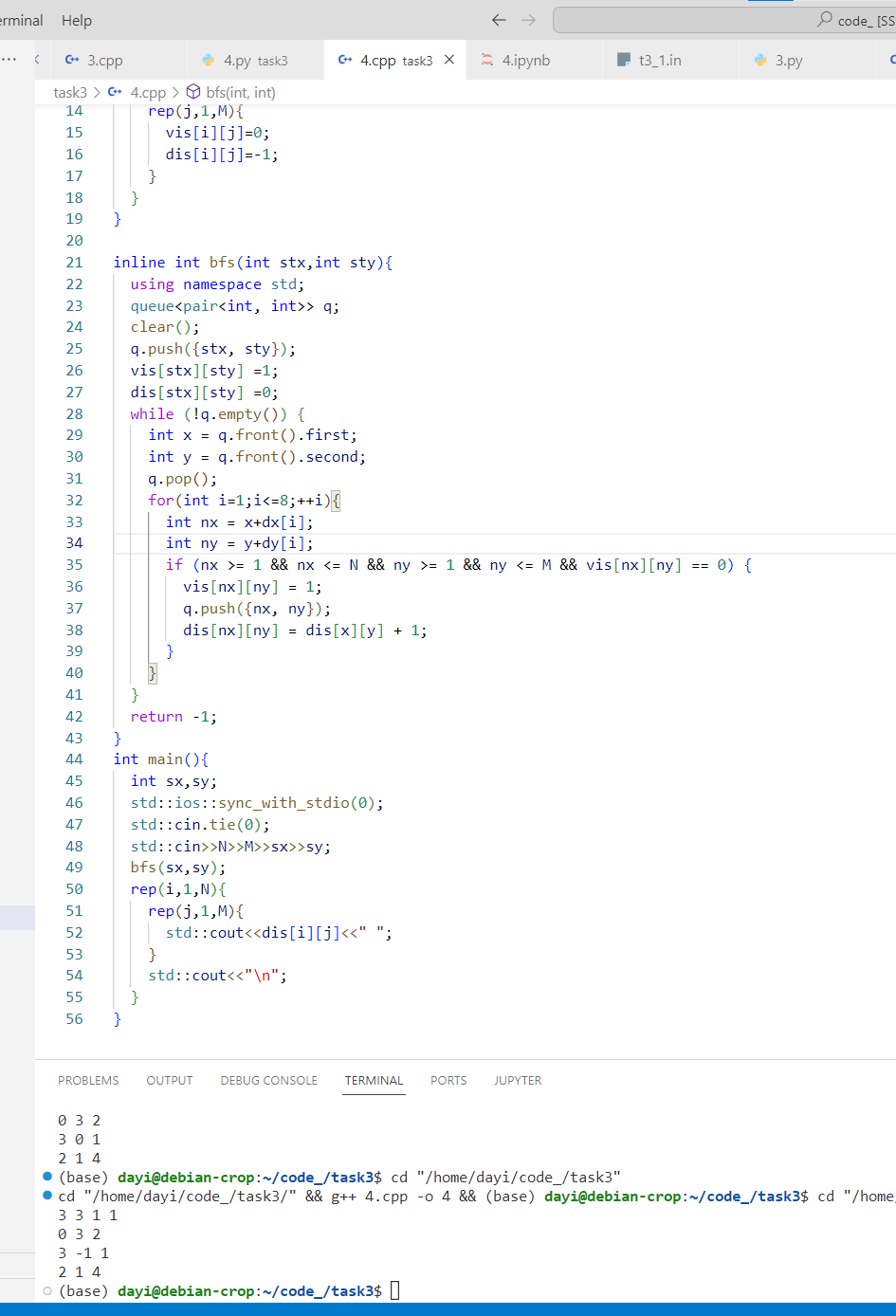
C++:

Python:

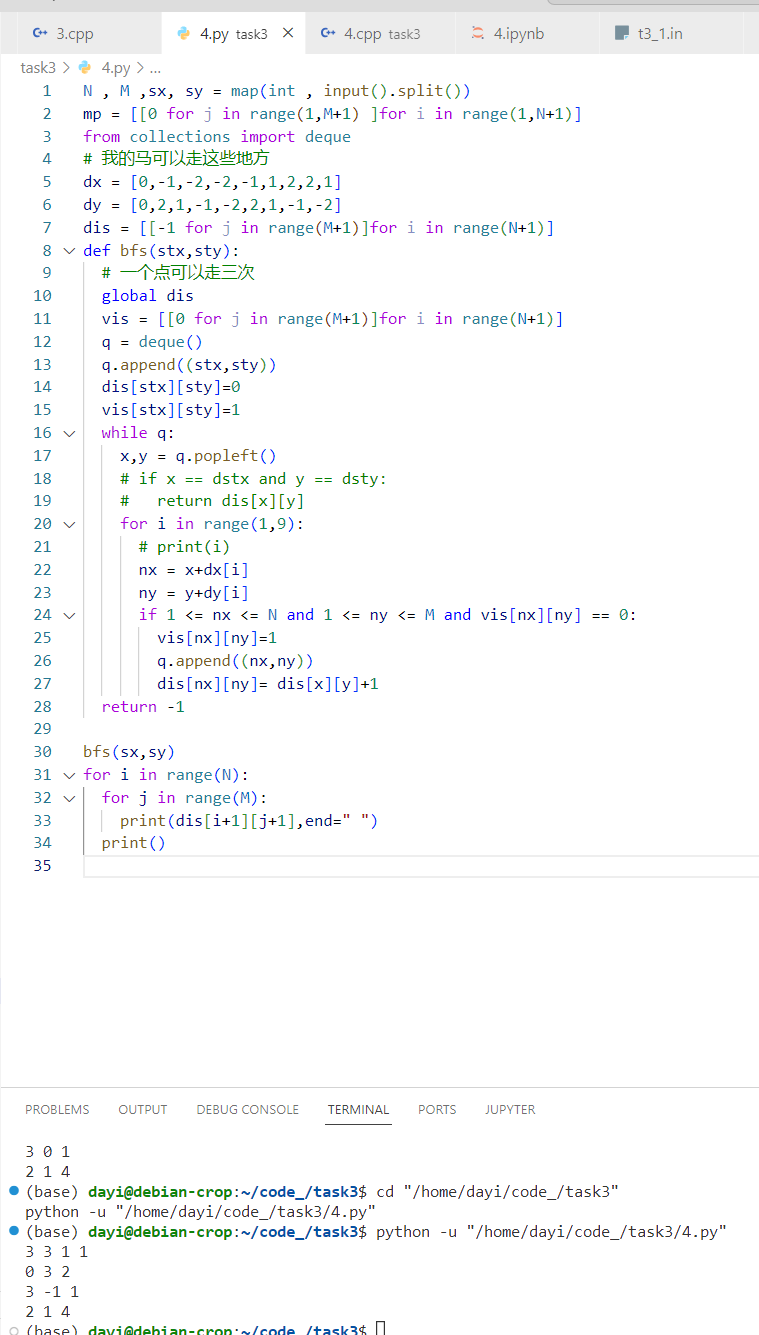
错怪 Python 了

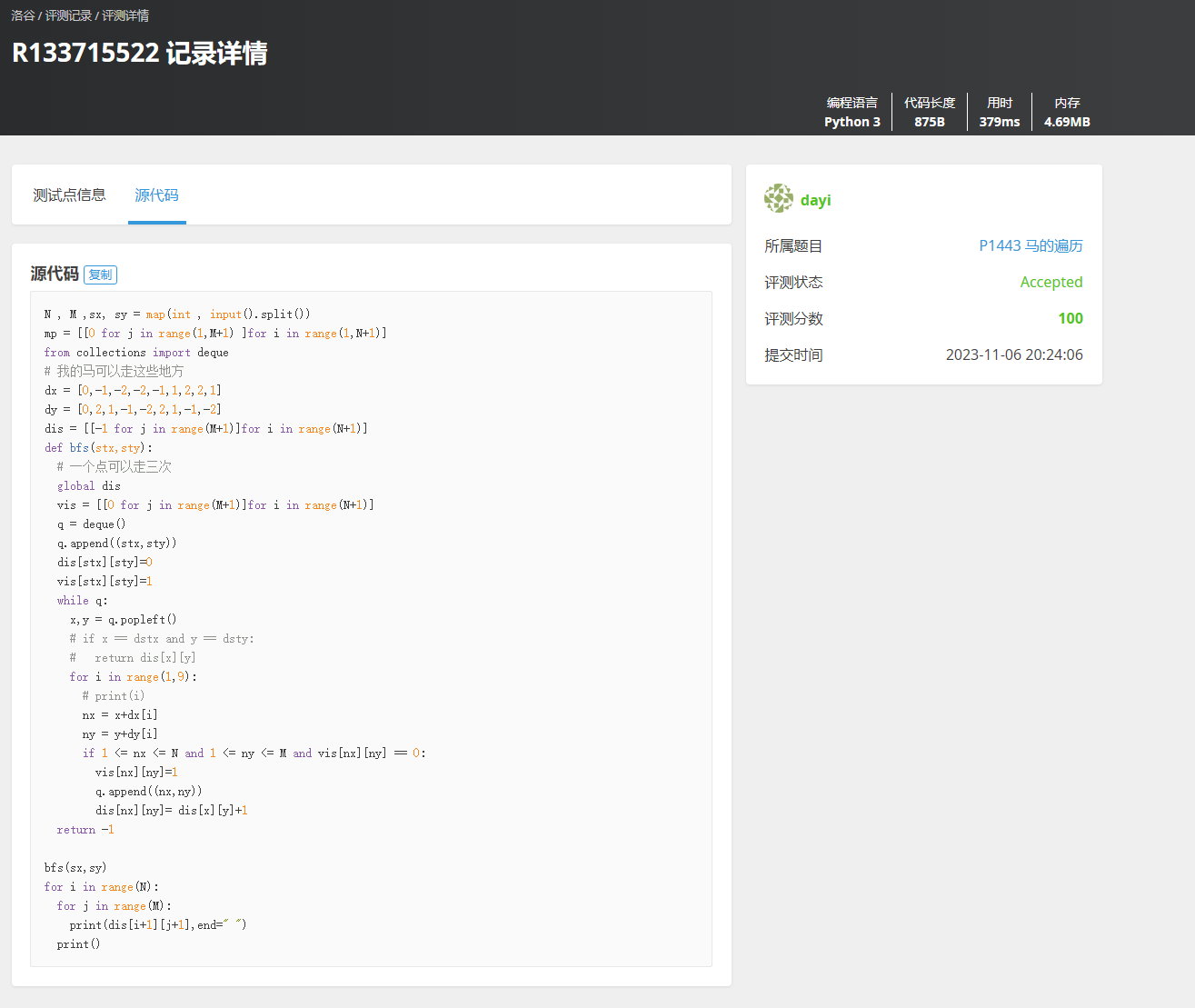
最后的代码：

C++

#include<bits/stdc++.h>

const int maxn = 800;
const int maxm = 800;
int dx[] = {0,-1,-2,-2,-1,1,2,2,1};
int dy[] = {0,2,1,-1,-2,2,1,-1,-2};
int N,M;
int vis[maxn][maxm];
int dis[maxn][maxm];
#define rep(i,x,y) for(int i=x;i<=y;++i)

inline void clear(){
  rep(i,1,N){
    rep(j,1,M){
      vis[i][j]=0;
      dis[i][j]=-1;
    }
  }
}

inline int bfs(int stx,int sty){
  using namespace std;
  queue<pair<int, int>> q;
  clear();
  q.push({stx, sty});
  vis[stx][sty] =1;
  dis[stx][sty] =0;
  while (!q.empty()) {
    int x = q.front().first;
    int y = q.front().second;
    q.pop();
    for(int i=1;i<=8;++i){
      int nx = x+dx[i];
      int ny = y+dy[i];
      if (nx >= 1 && nx <= N && ny >= 1 && ny <= M && vis[nx][ny] == 0) {
        vis[nx][ny] = 1;
        q.push({nx, ny});
        dis[nx][ny] = dis[x][y] + 1;
      }
    }
  }
  return -1;
}
int main(){
  int sx,sy;
  std::ios::sync_with_stdio(0);
  std::cin.tie(0);
  std::cin>>N>>M>>sx>>sy;
  bfs(sx,sy);
  rep(i,1,N){
    rep(j,1,M){
      std::cout<<dis[i][j]<<" ";
    }
    std::cout<<"\n";
  }
}

python:

N , M ,sx, sy = map(int , input().split())
mp = [[0 for j in range(1,M+1) ]for i in range(1,N+1)]
from collections import deque
# 我的马可以走这些地方
dx = [0,-1,-2,-2,-1,1,2,2,1]
dy = [0,2,1,-1,-2,2,1,-1,-2]
dis = [[-1 for j in range(M+1)]for i in range(N+1)]
def bfs(stx,sty):
  # 一个点可以走三次
  global dis
  vis = [[0 for j in range(M+1)]for i in range(N+1)]
  q = deque()
  q.append((stx,sty))
  dis[stx][sty]=0
  vis[stx][sty]=1
  while q:
    x,y = q.popleft()
    # if x == dstx and y == dsty:
    #   return dis[x][y]
    for i in range(1,9):
      # print(i)
      nx = x+dx[i]
      ny = y+dy[i]
      if 1 <= nx <= N and 1 <= ny <= M and vis[nx][ny] == 0:
        vis[nx][ny]=1
        q.append((nx,ny))
        dis[nx][ny]= dis[x][y]+1
  return -1

bfs(sx,sy)
for i in range(N):
  for j in range(M):
    print(dis[i+1][j+1],end=" ")
  print()

第八章回溯算法

题目 1 2 总分
分数

第八章回溯算法T2

题目描述

2.汉诺塔。
有三根柱子，用s1、s2、s3；表示。s1上有n个大小不一的盘子，最大的在最下面。我们想要将这n个盘子移到s2上，每一次只能移动一个盘子，并且在大盘子上不能放小盘子上面。请输出移动盘子的步骤。
比如：

移动第1次A-＞B
移动第2次A-＞C
移动第3次B-＞C

题目解析

其实很经典的问题啦，把柱子移动好即可。

汉诺塔：

  1. 将\(n-1\)个柱子从\(A->B\)柱，此时\(C\)为工具柱
  2. 将\(A\)柱下面最大的盘子移动到\(C\)
  3. 将\(B\)柱下面\(n-1\)个盘子（看做整体）移动到C柱（A为工具柱）

代码

# 汉诺塔
# 将N-1个盘子从A->B（C为工具)
# 将A地下最大的盘子移动到C
# 将B柱的N-1盘子移动到C
cnt = 0
def move(n,a,b,c):
  global cnt
  if n==0:
    return 1
  move(n-1,a,c,b)#C为工具柱 将N-1个盘子从A->B（C为工具)
  cnt+=1
  print(f"移动第{cnt}次，{a}-->{c}") # 将B柱的N-1盘子移动到C
  move(n-1,b,a,c) # 将B柱的N-1盘子移动到C
move(10,'s1','s2','s3')

运行截图

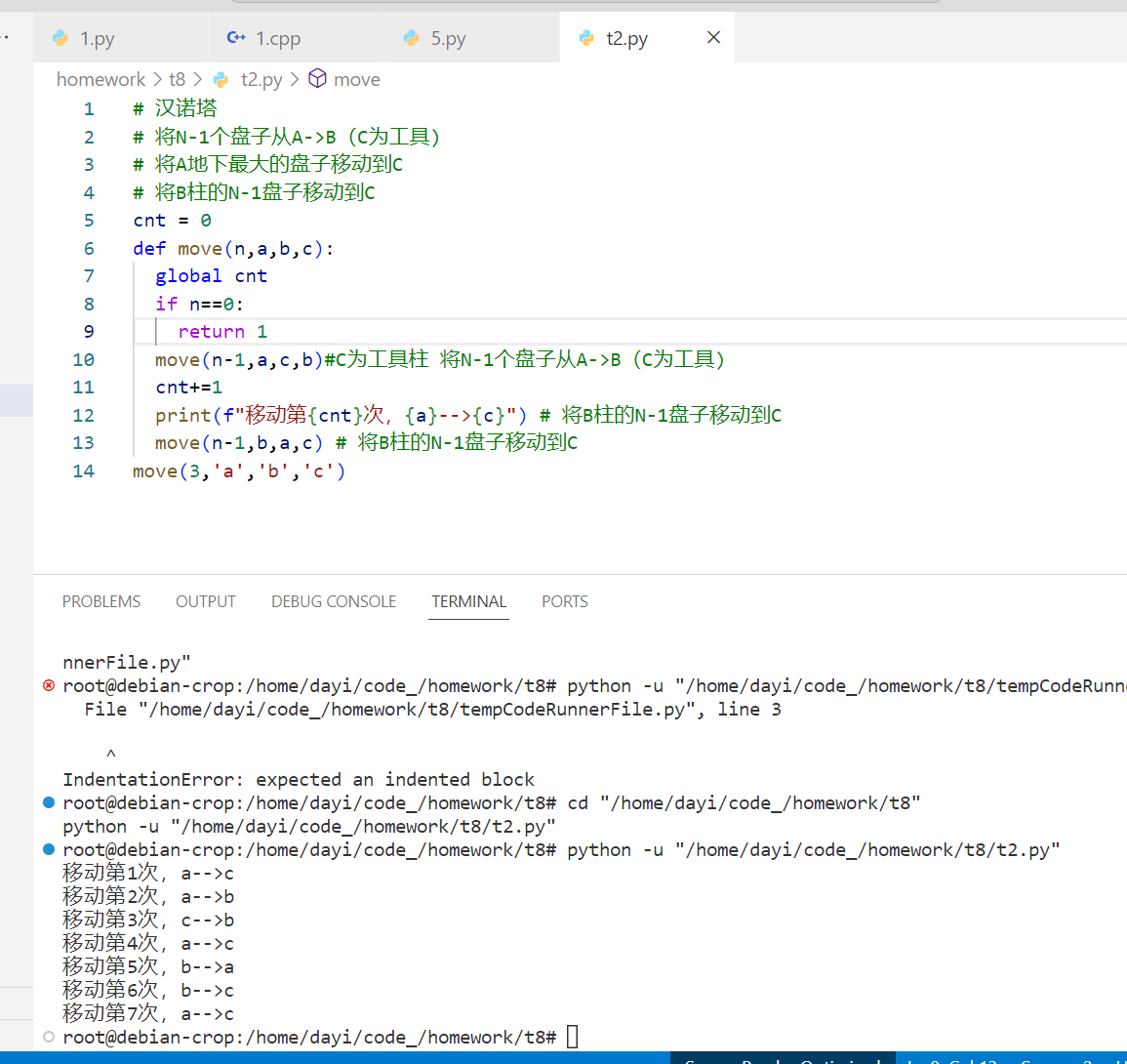
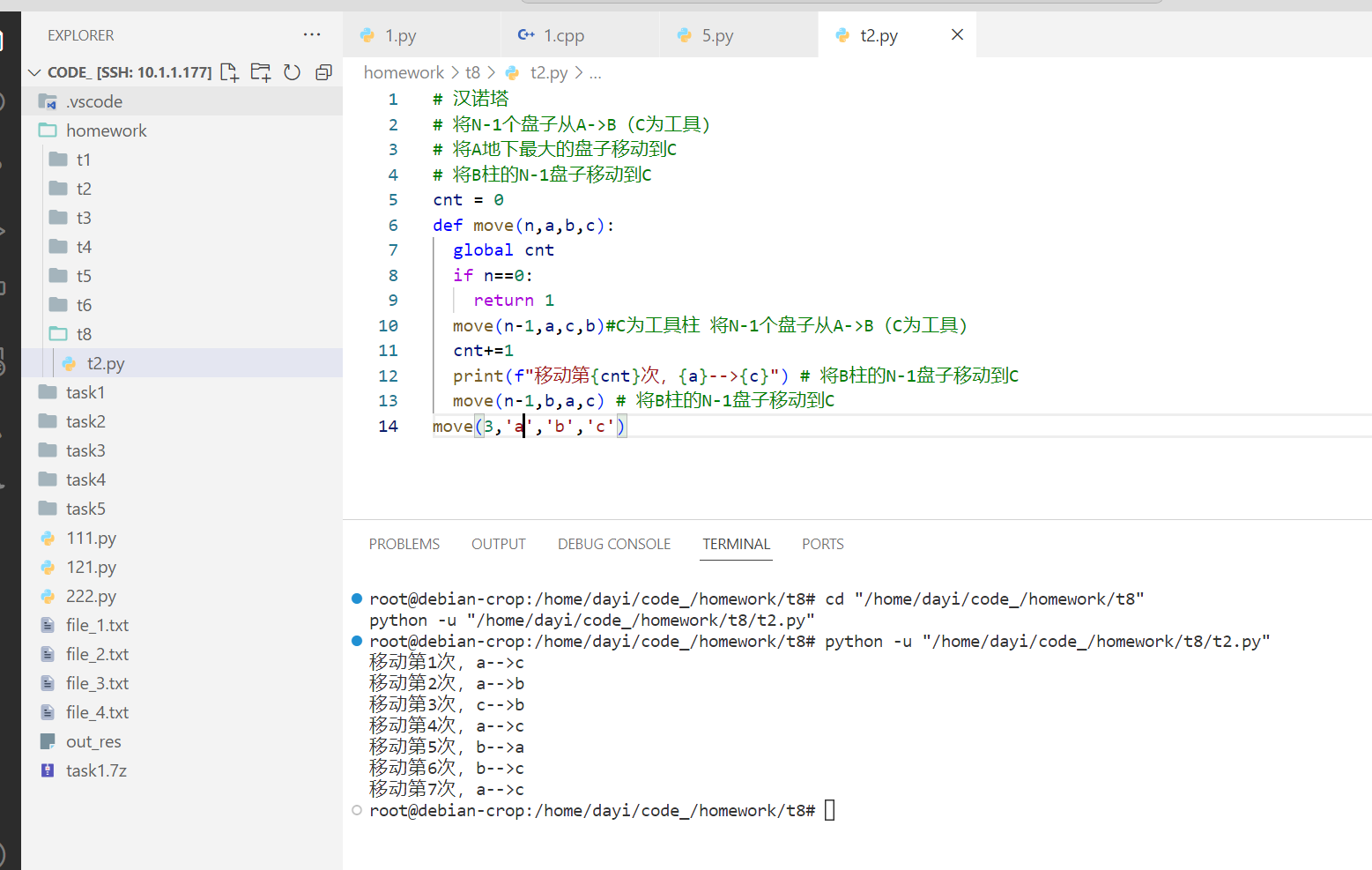
10次的时候：

第八章回溯算法T4

题目描述：

4.给定一个仅包含数字1～9的字符串，如图8-25所示，返回所有它能表示的字母组合。给出数字到字母的映射如下。
示例：
输入：＂12＂
输出： ［＂ad＂， ＂ae＂， ＂af＂， ＂bd＂， ＂be＂， ＂bf＂， ＂cd＂， ＂ce＂， ＂cf＂］

题目解析

用DFS搜索就可以啦，每层枚举当前数字对应字母的所有的情况，在DFS的末尾合并输出结果即可。

先写一个数字到字母的映射表 mp。

在函数 dfs 中：

  • 参数 inputs 是输入的数字字符串
  • idx 是当前递归的索引位置（初始值为 0）
  • path 是到目前为止建立的字符串组合（初始为空字符串）
  • res 是存储所有可能组合的结果列表（初始为 None，然后在函数中初始化为空列表）。

具体：

  1. 如果 res 是 None，即在第一次函数调用时，初始化它为一个空列表。
  2. 如果 idx 等于 inputs 的长度，意味着已经到达了输入字符串的末尾，当前的 path 就是一个完整的组合，将其添加到 res 列表中。
  3. 在每一层递归中，遍历 inputs[idx]，即当前索引数字对应的所有可能的字母。
  4. 对于每一个可能的字母，将其添加到 path 上，并递归调用 dfs，同时索引 idx 加 1，表示移动到下一个数字上。
  5. 递归继续，直到 idx 等于 inputs 的长度，这时 path 被添加到结果列表 res 中。
  6. 一旦完成了所有可能的字母组合的探索，返回 res 列表。

代码

运行结果

  • 输入"12"

  • 输入"114514"

第九章DP

题目 1 总分
分数

第九章DP--题目

用动态规划求下列问题：

在A处有一水库，现需要从A点铺设一条管道到E点，边上的数字表示与其相连的两个地点之间所需修建的管道长度，用c数组表示，例如c(A，B1)=2。现要找出一条从A到E的修建线路，使得所需修建的管道长度最短。

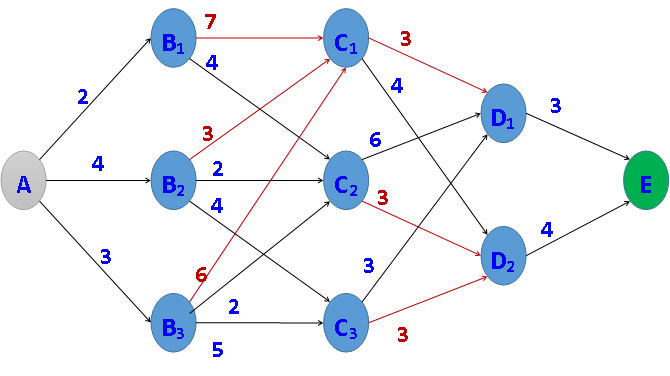
image-20231126204842485

题目解析

将问题视为一个有向无环图（DAG），并且有一个明确的顺序（从 A 到 E）。

在 DAG 中，我们可以按照拓扑排序的顺序来应用 DP，自底向上地计算每个节点到目标节点的最短路径长度。

设 dp[v] 表示从节点 v 到目的地 E 的最短路径长度。对于图中的每个节点 v，我们可以按照以下方式更新 dp[v]：

\[dp[v] = \min_{(v, u) \in E}(c(v, u) + dp[u]) \]

这里，\(E\) 表示边的集合，\(c(v, u)\) 表示从节点 v 到节点 u 的边的权重。对于最终的目的地节点 E，dp[E] = 0，因为从 E 到 E 的最短路径长度是 0。

可以从终点 E 开始，反向遍历图中的每个节点，并计算 dp[v]。
最终，dp[A] 将给出从 A 到 E 的最短路径长度。

构造输入：

其中，11 表示\(A_1\)

  • 11(表示\(A_1\)） 21（表示\(B_1\)）2（权值）
  • 11 22（表示\(B_2\)） 4(权值)
10 19
11 21 2
11 22 4
11 23 3
21 31 7
21 32 4
22 31 3
22 32 2
22 33 4
23 31 6
23 33 5
23 32 2
31 41 3
31 42 4
32 41 6
32 42 3
33 42 3
33 43 3
41 51 3
42 51 4

非映射：

10 19
A1 B1 2
A1 B2 4
A1 B3 3
B1 C1 7
B1 C2 4
B2 C1 3
B2 C2 2
B2 C3 4
B3 C1 6
B3 C3 5
B3 C2 2
C1 D1 3
C1 D2 4
C2 D1 6
C2 D2 3
C3 D2 3
C3 D3 3
D1 E1 3
D2 E1 4

答案大概是这个：

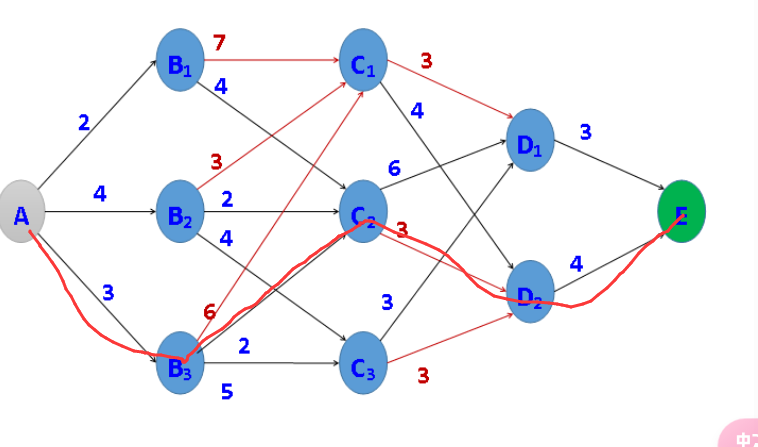
然后DP跑一下即可，同时记录下更新的前驱。

代码

#include<bits/stdc++.h>
const int maxn=11451;
const int inf = 0x3f3f3f3f;
struct Edge{
  int u,v,w,nxt;
}edge[maxn<<1];
int fst[maxn];
int cnt;


inline void addedge(int u,int v,int w){
  edge[++cnt].u=u,edge[cnt].v=v,edge[cnt].w=w;
  edge[cnt].nxt=fst[u];
  fst[u]=cnt;
}

int N,M;
int dp[maxn];
int pre[maxn];//前驱
int cnt_node;

std::map<std::string,int> mp;//映射字母和节点

inline int solve(int src, int dst) {
    for (int i = 1; i <= cnt_node; ++i) dp[i] = inf;
    memset(pre, -1, sizeof(pre));
    dp[src] = 0; // 初始化源点到自己的距离为0
    for(int i = 1; i<N; ++i) { // 对所有边进行N-1次松弛
        for(int j = 1; j <= cnt; ++j) {
            int u = edge[j].u;
            int v = edge[j].v;
            int w = edge[j].w;
            if (dp[u] < inf && dp[u] + w < dp[v]) { // 如果可以更新到更短的路径
                dp[v] = dp[u] + w; // 更新dp数组
                pre[v] = u; // 记录前驱节点
            }
        }
    }
    return dp[dst]; // 返回从源点到目标点的最短路径长度
}


void print_path(int dst) {
  using namespace std;
  if(pre[dst] == -1) {
    for(map<string,int>::iterator it = mp.begin();it!=mp.end();it++){
      if(it->second==dst){
        std::cout << it->first; // 打印当前节点
        break;
      }
    }
    return;
  }
  print_path(pre[dst]); // 递归打印前驱节点的路径
  
  for(map<string,int>::iterator it = mp.begin();it!=mp.end();it++){
    if(it->second==dst){
      std::cout << " -> " << it->first; // 打印当前节点
      break;
    }
  }
}

int main(){
  using namespace std;
  // freopen("in.in","r",stdin);
  cin>>N>>M;
  for(int i=1;i<=M;++i){
    string u,v;
    int w;
    cin>>u>>v>>w;
    if(!mp[u])mp[u]=++cnt_node;
    if(!mp[v])mp[v]=++cnt_node;
    addedge(mp[u],mp[v],w);
  }
  int res = solve(mp["A1"],mp["E1"]);
  cout<<res<<"\n";
  cout<<"PATH:\n";
  int dst = mp["E1"];
  print_path(dst);cout<<"\n";
}

运行结果

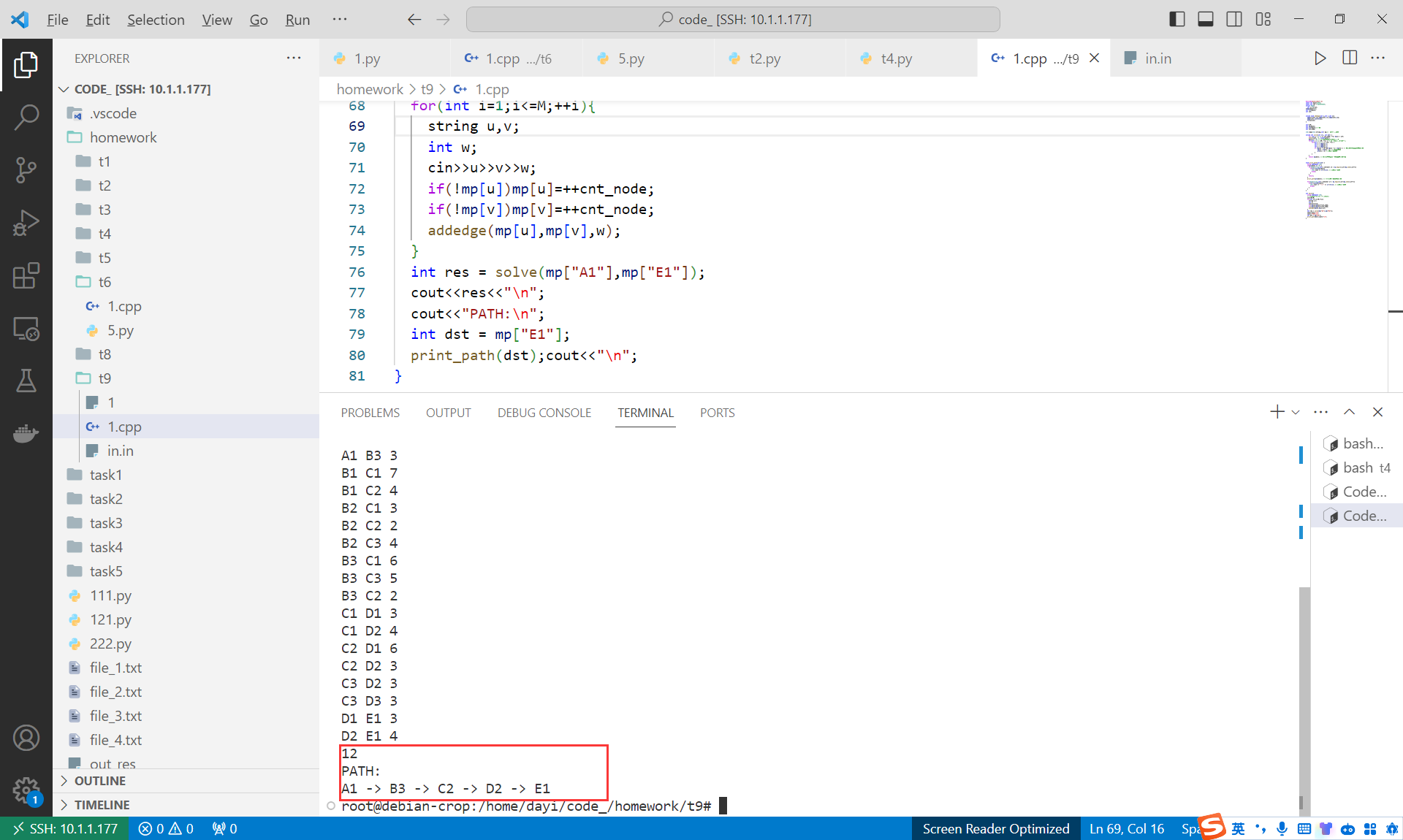
第十章贪心算法

第十章贪心算法--活动安排

实验题目也有

假设有一个需要使用某一资源的n个活动所组成的集合S，S={1，…，n}。该资源任何时刻只能被一个活动所占用，活动i有一个开始时间bi和结束时间ei（bi<ei），其执行时间为ei-bi，假设最早活动执行时间为0。
一旦某个活动开始执行，中间不能被打断，直到其执行完毕。若活动i和活动j有bi≥ej或bj≥ei，则称这两个活动兼容。
设计算法求一种最优活动安排方案，使得所有安排的活动个数最多。

11
1 4
3 5
0 6
5 7
3 8
5 9
6 10
8 11
8 12
2 13 
12 15

代码

如下

# 时间复杂度 O(nlogn)（排序）
n = eval(input())
ls = [ ]
for i in range(n):
  st,end = map(int,input().split())
  ls.append((st,end))
ls.sort(key=lambda x:x[1])
# [(1, 3), (2, 5), (4, 6), (1, 7)]
# print(ls)
# vis = [0 for i in range(ls[-1][1]+10)]
now = 0
ans = 1 # 选了排序后的第一个
for i,v in enumerate(ls):
  print(v)
  # 如果起始时间大于5等于现在的终止时间（注意集合开闭）
  if v[0]>=ls[now][1]:
    now = i
    ans+=1
print(ans)

输出选择的活动：

# 时间复杂度 O(nlogn)（排序）
n = eval(input())
ls = []
for i in range(n):
  st,end = map(int,input().split())
  ls.append((st,end))
ls.sort(key=lambda x:x[1])
# 选择第一个活动
print("sel:",ls[0])
now = 0
ans = 1
for i,v in enumerate(ls):
  if v[0]>=ls[now][1]:
    print("sel:",str(v))
    now = i
    ans+=1
print(ans)

运行结果

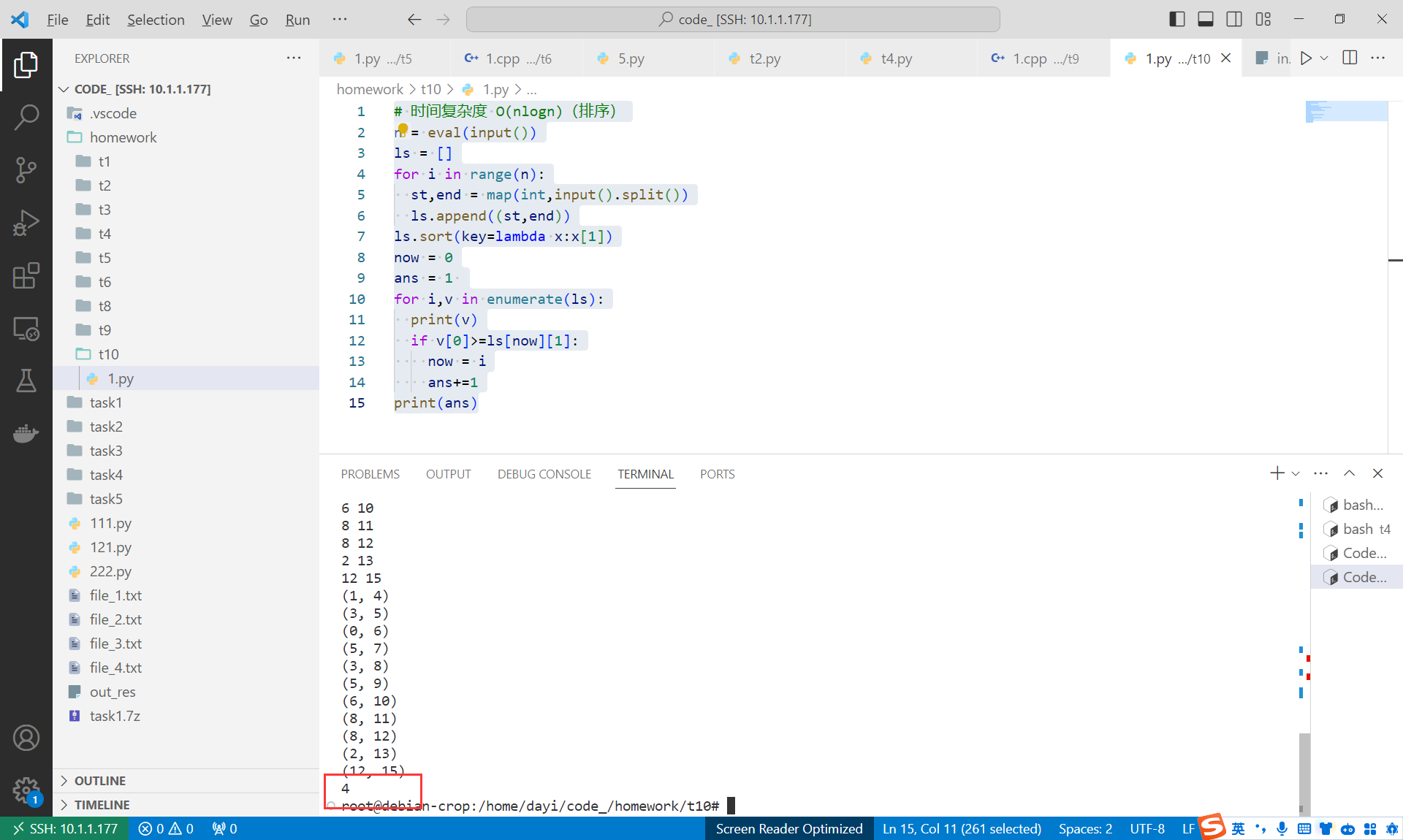
输出选择的活动:

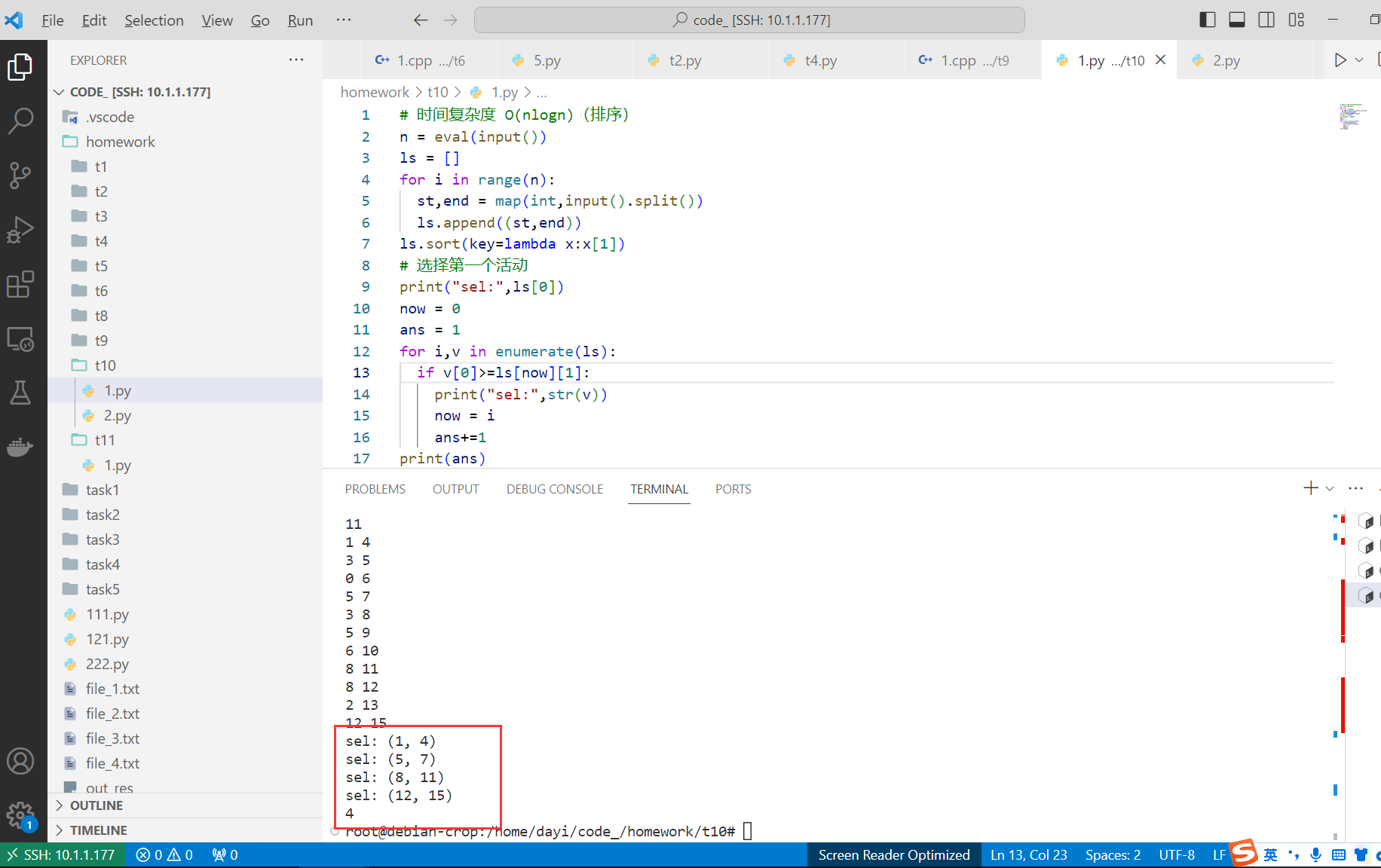
第十章贪心算法--活动安排-实验报告

2.活动安排问题

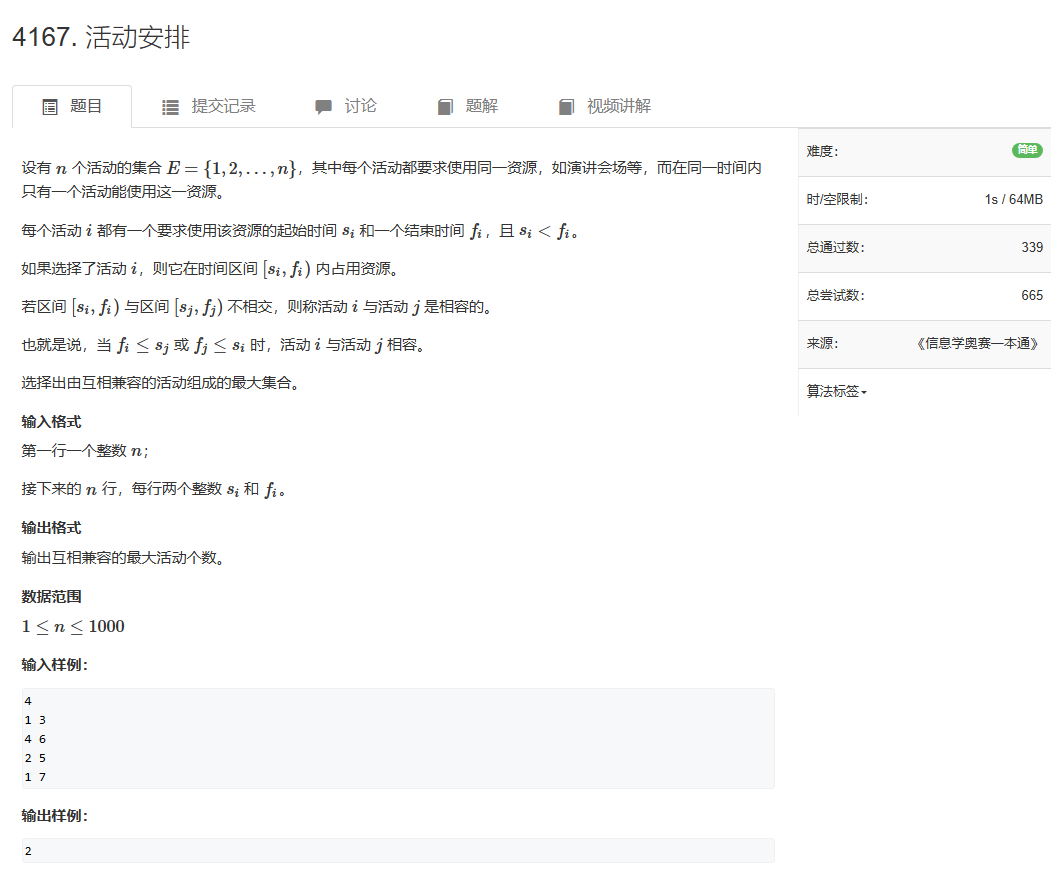
设有 n 个活动的集合 \(E=\{1,2,..,n\}\)，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。
每个活动 i 都有一个要求使用该资源的起始时间 \(s_i\) 和一个结束时间 \(f_i\)，且 \(s_i<f_i\)。
如果选择了活动 i ，则它在时间区间 \([s_i,f_i)\) 内占用资源。
若区间 \([s_i,f_i)\) 与区间 \([s_j,f_j)\) 不相交，则称活动 i 与活动 j 是相容的。也就是说，当 \(f_i≤s_j\) 或 \(f_j≤s_i\) 时，活动 i 与活动 j 相容。
选择出由互相兼容的活动组成的最大集合。

这道题是纯贪心啦（DP也能做）：

总是选择结束时间最早的活动，这样留给其它活动的时间就最多了，选择后使得对其他活动影响最小。（证明就不证了）

  1. 将所有活动按照结束时间进行排序。
  2. 选择结束时间最早的活动。
  3. 剔除所有与已选择活动时间上有冲突的活动。
  4. 重复步骤 2 和 3，直到没有剩余的活动为止。
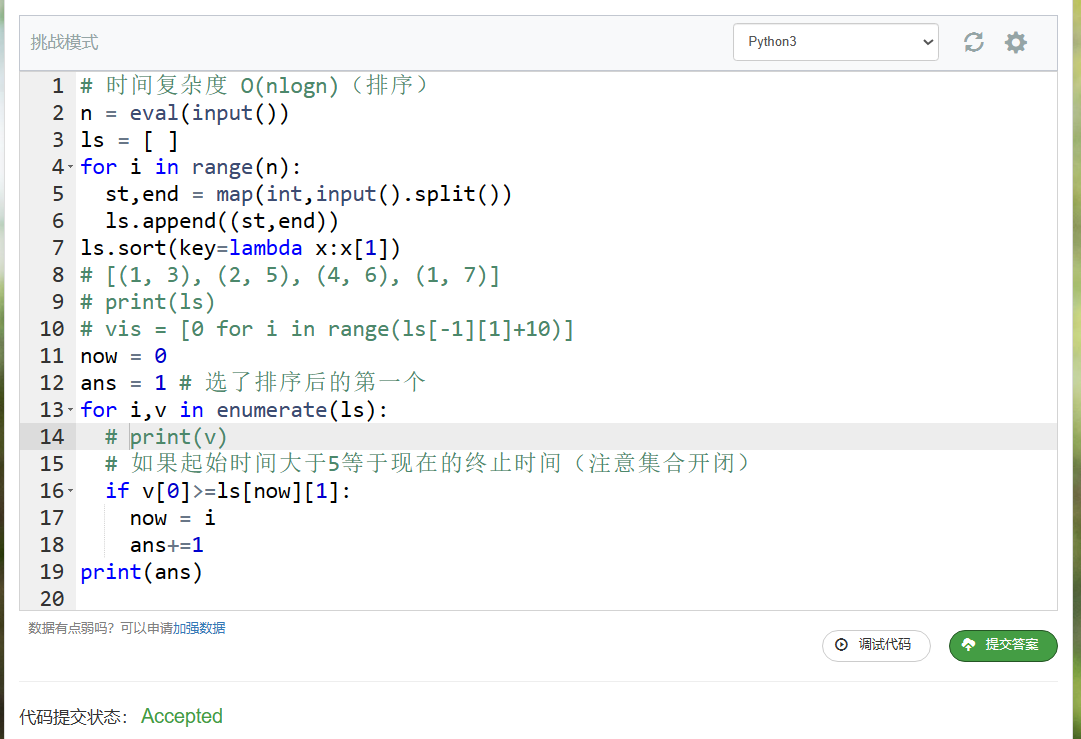
# 时间复杂度 O(nlogn)（排序）
n = eval(input())
ls = [ ]
for i in range(n):
  st,end = map(int,input().split())
  ls.append((st,end))
ls.sort(key=lambda x:x[1])
# [(1, 3), (2, 5), (4, 6), (1, 7)]
# print(ls)
# vis = [0 for i in range(ls[-1][1]+10)]
now = 0
ans = 1 # 选了排序后的第一个
for i,v in enumerate(ls):
  print(v)
  # 如果起始时间大于5等于现在的终止时间（注意集合开闭）
  if v[0]>=ls[now][1]:
    now = i
    ans+=1
print(ans)

第十一章分治算法

第十一章分治算法

题目 1 2 3 总分
分数

第1题，第2题，第3题

第十一章分治算法-T1

题目描述

4有四种划分方式：1＋1＋1＋11＋1＋2.1＋3.2＋2.5有六种划分方式：1＋1＋1＋1＋1.1＋1＋1＋2，1＋1＋3，1＋2＋2，1＋4，3＋2。给定一个数字n和子集1，2，3.…，n-1，请用数组输出所有不同的划分方式。例如：
输入：4
输出：［(1，1，1，1），(1，1，2)，（1，3)，（2，2］]

题目解析

使用 DFS 来找到所有可能的整数划分。

  • 如果 n 变为 0，这意味着当前的 cur 数组是 N 的一个有效划分，因为加起来正好等于 N。将这个划分作为元组添加到结果列表 res 中，并返回。

  • 循环遍历从 st（起始索引）到 len(nums) 的所有整数。每次循环，选择一个数 nums[i-1] 并从 n 中减去这个数，表示将这个数纳入当前划分。

  1. 递归的调用：如果 nums[i-1] 小于或等于 n，这意味着我们可以将这个数作为当前划分的一部分。我们递归地调用 fn，传递新的 n 值（n - nums[i-1]），索引 i（确保不会选择小于当前数字的数字，从而避免重复），以及更新的当前划分 cur + [nums[i-1]]。

  2. 避免重复的划分：通过在每次递归调用中传递 i 作为起始索引，我们确保不会出现重复的划分。这是因为我们总是选择当前数字或更大的数字，从而保持了划分中数字的顺序。

  3. 结束递归：当我们尝试所有可能的数字，并且 n 不再减少到 0，递归调用将结束。如果 n 变为负数，我们不做任何事情就返回，因为这意味着当前的划分无法加起来等于 N。

整个过程可以视为一棵树，其中每个节点代表一个划分的决策。DFS 遍历这棵树，探索所有可能的路径，即整数 N 的所有可能划分。

  • res[0:len(res)-1] 从结果列表 res 中省略了最后一个元素。

代码

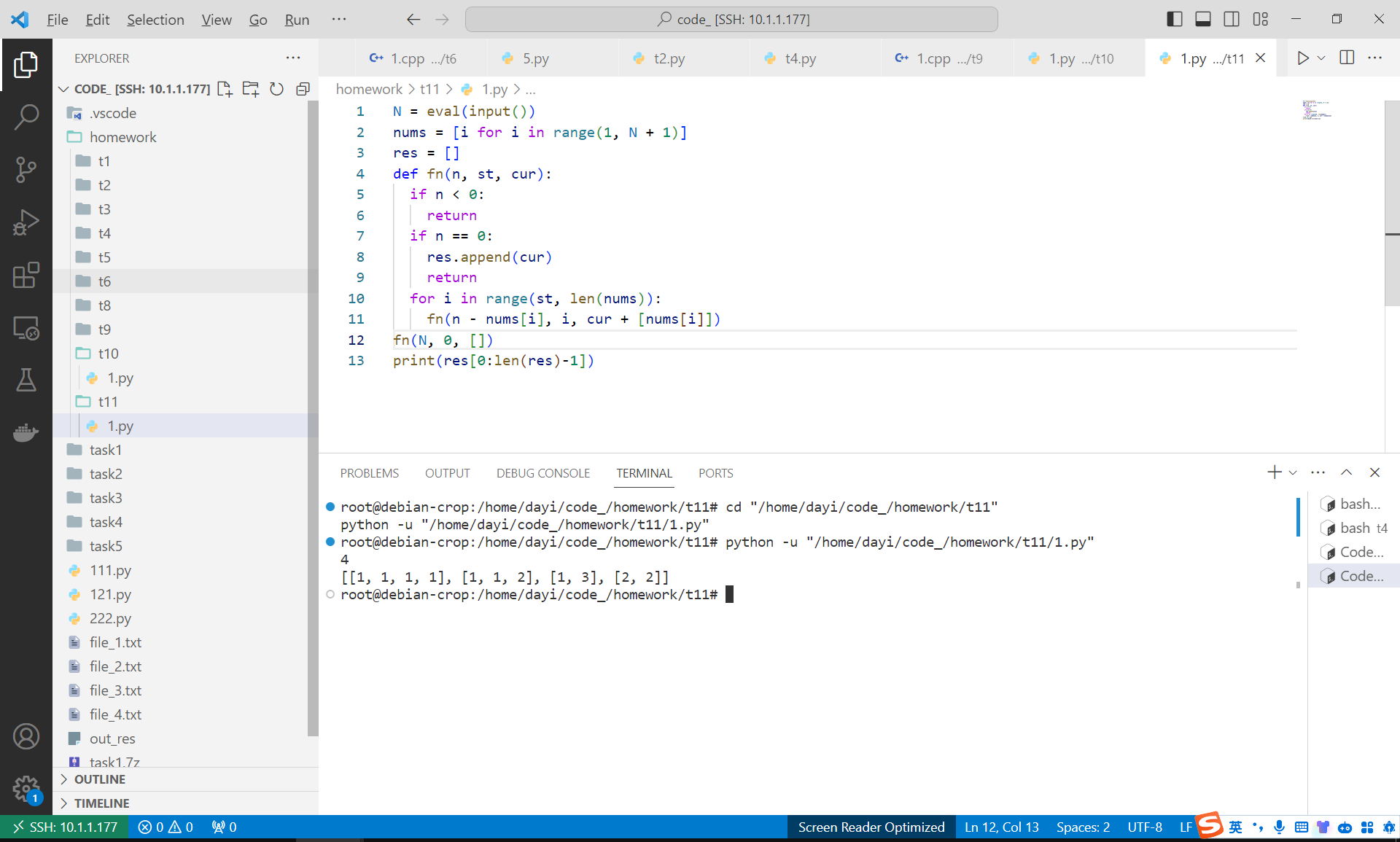
N = eval(input())
nums = [i for i in range(1, N + 1)]
res = []
def fn(n, st, cur):
  if n < 0:
    return
  if n == 0:
    res.append(cur)
    return
  for i in range(st, len(nums)):
    fn(n - nums[i], i, cur + [nums[i]])
fn(N, 0, [])
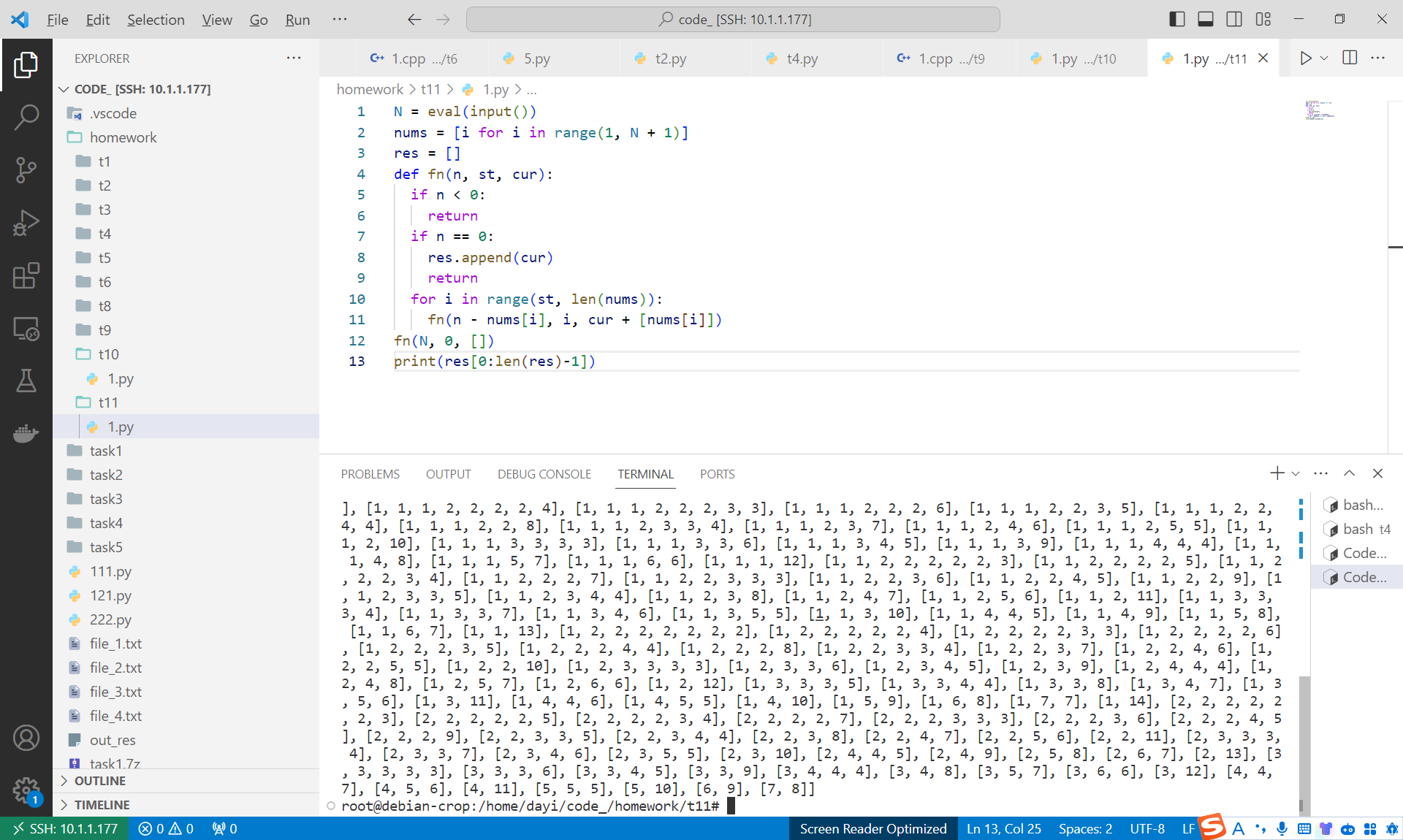
print(res[0:len(res)-1])

运行结果

N = 4

N=15

第十一章分治算法-T2

题目描述

给定一个没有重复数字的数组，输出第k小的元素。例如：
输入：[2,1,3,4,5,0,9],4
输出：3
输入：[6,-1,4,5,2,-10],2
输出：-1

题目解析

排序即可OVO

归并排序代码：

n = int(input())
ls = list(map(int, input().split()))
def merge_sort(l,r):
  if l>=r:
    return
  mid = (l+r)//2
  merge_sort(l,mid)
  merge_sort(mid+1,r)
  i,j = l,mid+1
  tmp = []
  while i<=mid and j<=r and i<=j:
    if ls[i]<ls[j]:
      tmp.append(ls[i])
      i+=1
    else:
      tmp.append(ls[j])
      j+=1
  while j<=r:
    tmp.append(ls[j])
    j+=1
  while i<=mid:
    tmp.append(ls[i])
    i+=1
  for i in range(l, r + 1):
    # 注意
    ls[i] = tmp[i - l]

merge_sort(0, len(ls) - 1)
print(" ".join(str(i) for i in ls))

快排代码：

n = int(input())
ls = list(map(int, input().split()))
def sort(l, r):
    if l >= r:
        return
    i = l - 1
    j = r + 1
    import random
    val = ls[random.randint(l,r)]
    while i < j:
        i += 1
        while i < r and ls[i] < val:
            i += 1
        j -= 1
        while j > l and ls[j] > val:
            j -= 1
        if i < j:
            ls[i], ls[j] = ls[j], ls[i]
    sort(l, j)
    sort(j + 1, r)
sort(0, len(ls) - 1)
print(" ".join(str(i) for i in ls))

运行结果

输入1：

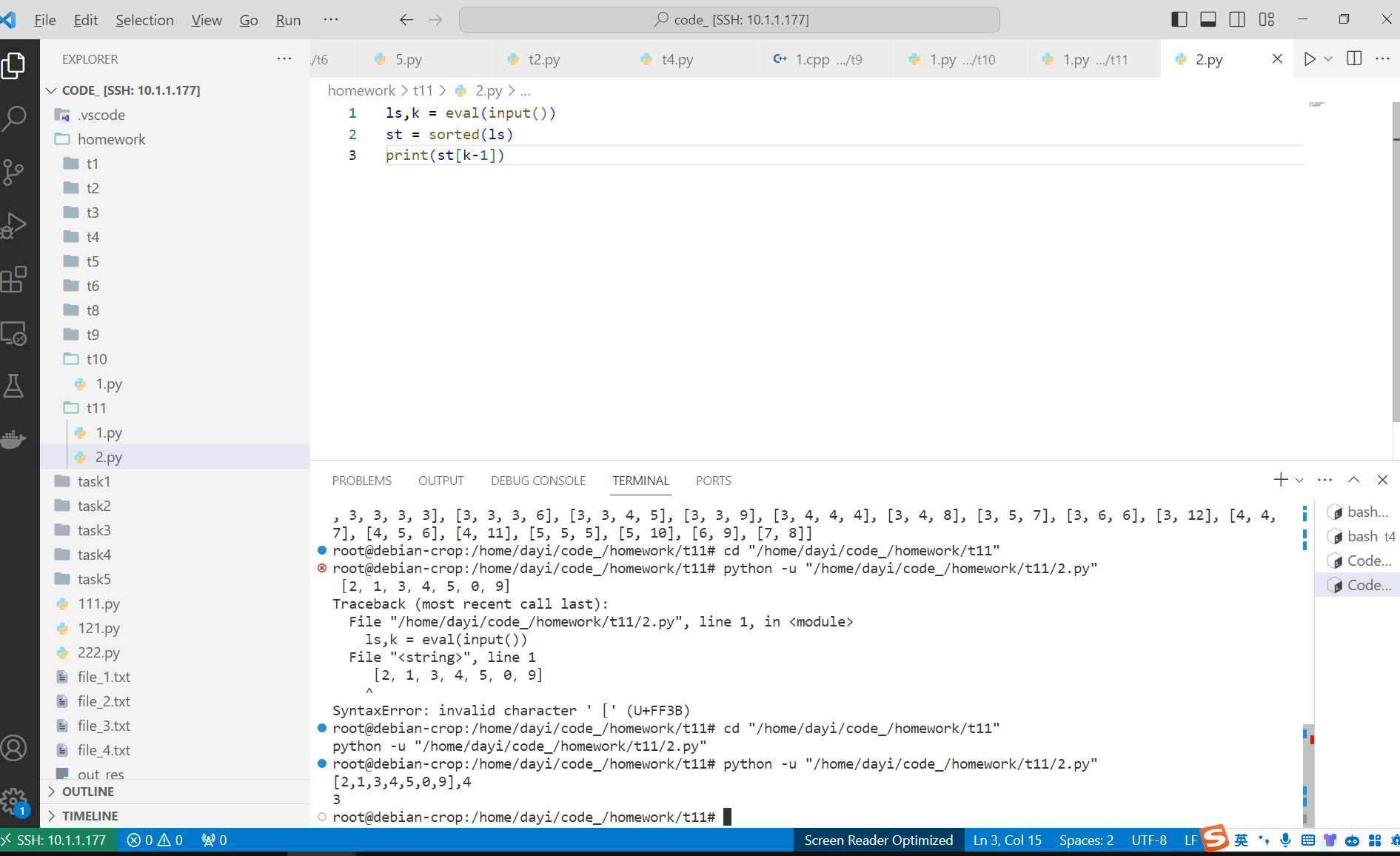
输入2：

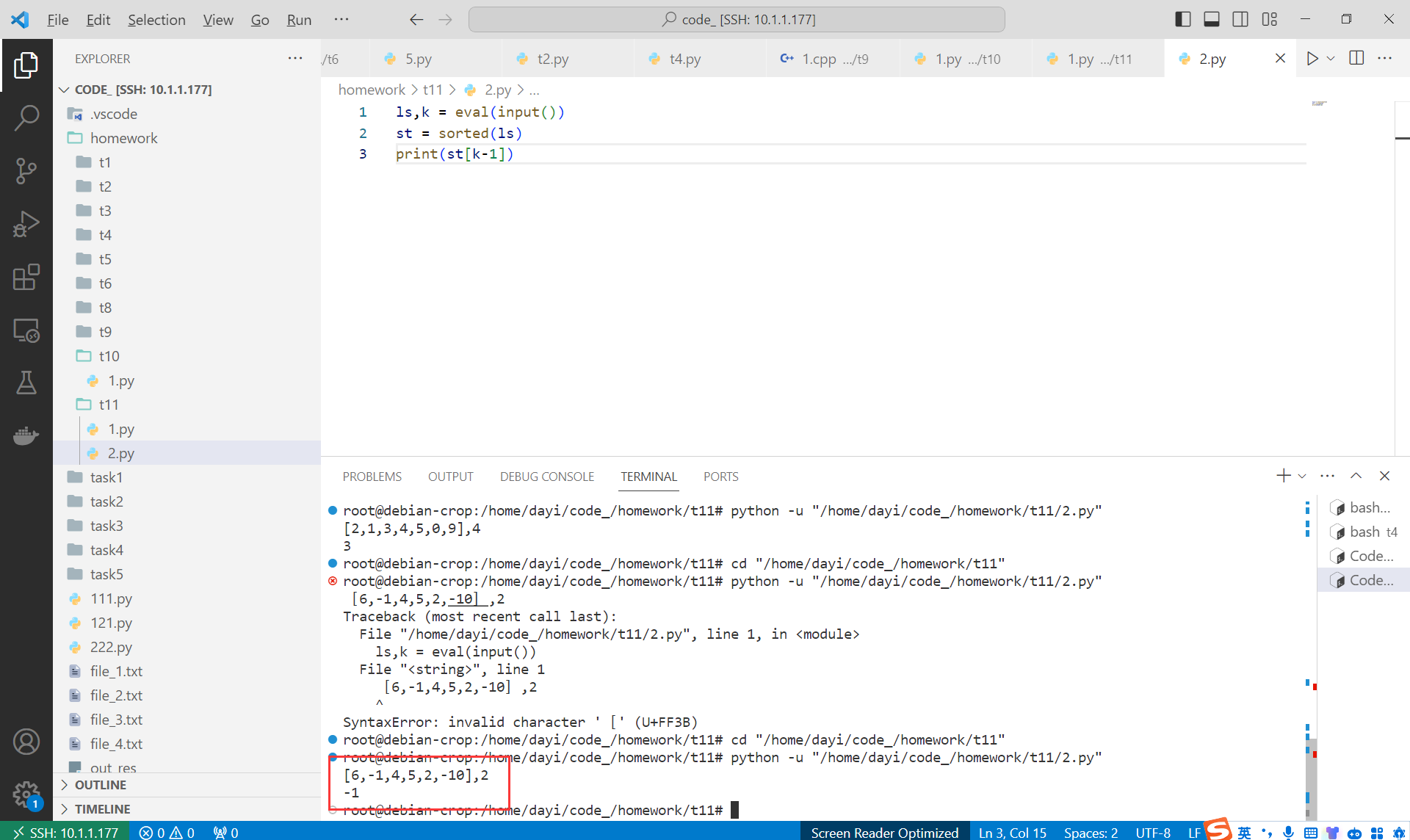
第十一章分治算法-T3

3.给定一个数组，输出拥有最大和的连续子数组。例如：

输入：[-1,2,3,-1]
输出：[2,3]
输入：[2,3,-4,5,-1,-10,4,3]
输出：[4,3]
输入：[-1,-2]
输出：[-1]

题目分析

Kadane算法可以在O（N）的时间里去求得答案。

  • 初始化：定义两个变量，max_sum 存储遍历到目前为止的最大子数组和，curr_sum 存储包含当前元素的最大子数组和。记录子数组的起始和结束索引，以便最后可以返回子数组本身。

  • 遍历整个数组，对于每个元素进行以下操作：

  • 更新 curr_sum：如果 current_sum 加上当前元素的和小于当前元素的值，说明从当前元素开始一个新的子数组可能会得到更大的和。

  • 更新 curr_sum 为当前元素的值，并记录新子数组的起始位置。

  • 如果 curr_sum 加上当前元素的和更大，则累加当前元素的值到 curr_sum。

  • 更新 max_sum：在每一步中，我们检查 curr_sum 是否比 max_sum 大。如果是，我们更新 max_sum 为 curr_sum 的值，并更新记录子数组的起始和结束索引。

  • 处理特殊情况：如果数组中全部都是负数，则最大子数组和将是数组中的最大单个元素。

也可以枚举区间，双指针，然后O(N*2)

暴力！

  • 枚举区间长度。
  • 求最大区间
  • 全是负数情况
  • 两个指针

  1. 检查是否所有元素都是负数:

    • 检查输入数组 ls 是否所有元素都是负数。这是一个特殊情况，因为如果数组中所有元素都是负数，那么最大子数组和就是其中最大的单个元素。
    • 直接返回包含这个最大负数的数组。

  2. 初始化变量:

    • cmax 初始化为负无穷大。它用于存储当前找到的最大子数组和。
    • res 初始化为空数组。它将用于存储产生最大和的子数组。

  3. 遍历所有可能的子数组:

    • 使用两个嵌套的 for 循环来遍历数组中所有可能的子数组。外层循环 (l) 代表子数组的起始位置，内层循环 (r) 代表子数组的结束位置。
    • 对于每一对 (l, r)，提取子数组 ls[l:r+1] 并计算它的和。

  4. 更新最大和及对应的子数组:

    • 如果当前子数组的和大于之前记录的最大和 cmax，则更新 cmax 为这个新的最大值，并且更新 res 为当前的子数组。

  5. 返回结果:

    • 最后，返回和最大的子数组 res。

代码-枚举区间

#O（N*3）
ls = eval(input())
def calc():
  n = len(ls)
  # 检查是否所有元素都是负数
  if all(x < 0 for x in ls):
    return [max(ls)]
  cmax = -float('inf')
  res = []
  # 遍历所有可能长度的子数组
  for l in range(n):
    for r in range(l,n):
      tmp_ls = ls[l:r+1]
      tmp_sum = sum(tmp_ls)
      if tmp_sum > cmax:
        cmax = tmp_sum
        res = tmp_ls
  return res
print(calc())
ls = [-1, 2, 3, -1]
print(calc())
ls = [2, 3, -4, 5, -1, -10, 4, 3]
print(calc())
ls = [-1, -2]
print(calc())

➜  t11 python -u "/home/dayi/code_/homework/t11/t3_2.py"
[1,1,4,5,1,4,-123]
[1, 1, 4, 5, 1, 4]
[2, 3]
[4, 3]
[-1]
➜  t11

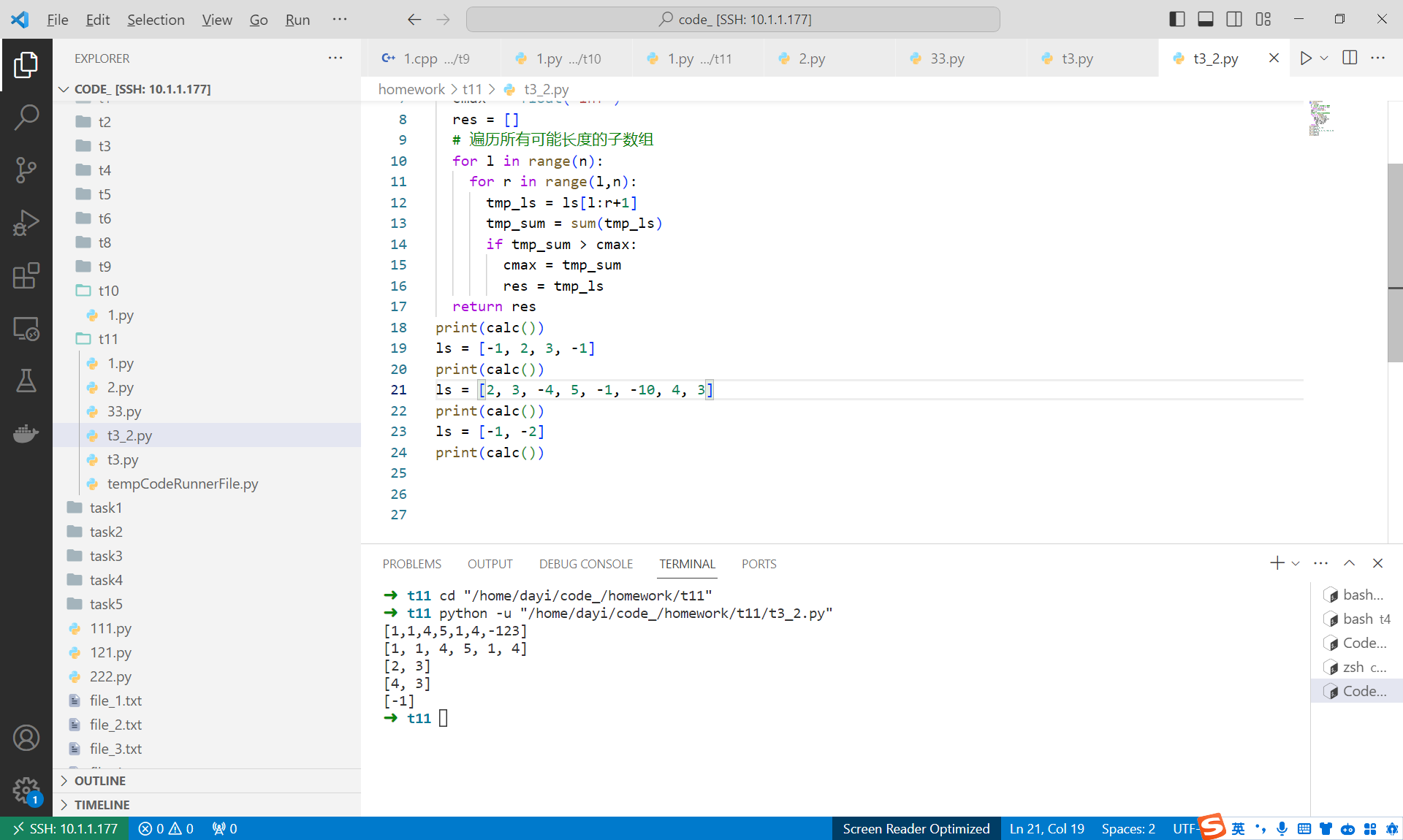
代码-Kadane

def solve(nums):
  max_sum = nums[0]
  curr_sum = nums[0]
  start = end = 0
  temp_start = 0
  for i in range(1, len(nums)):
    if nums[i] > curr_sum + nums[i]:
      curr_sum = nums[i]
      temp_start = i
    else:
      curr_sum += nums[i]
    if curr_sum > max_sum:
      max_sum = curr_sum
      start = temp_start
      end = i
    return nums[start:end + 1]
print(solve([-1, 2, 3, -1]))
print(solve([2, 3, -4, 5, -1, -10, 4, 3]))
print(solve([-1, -2]))

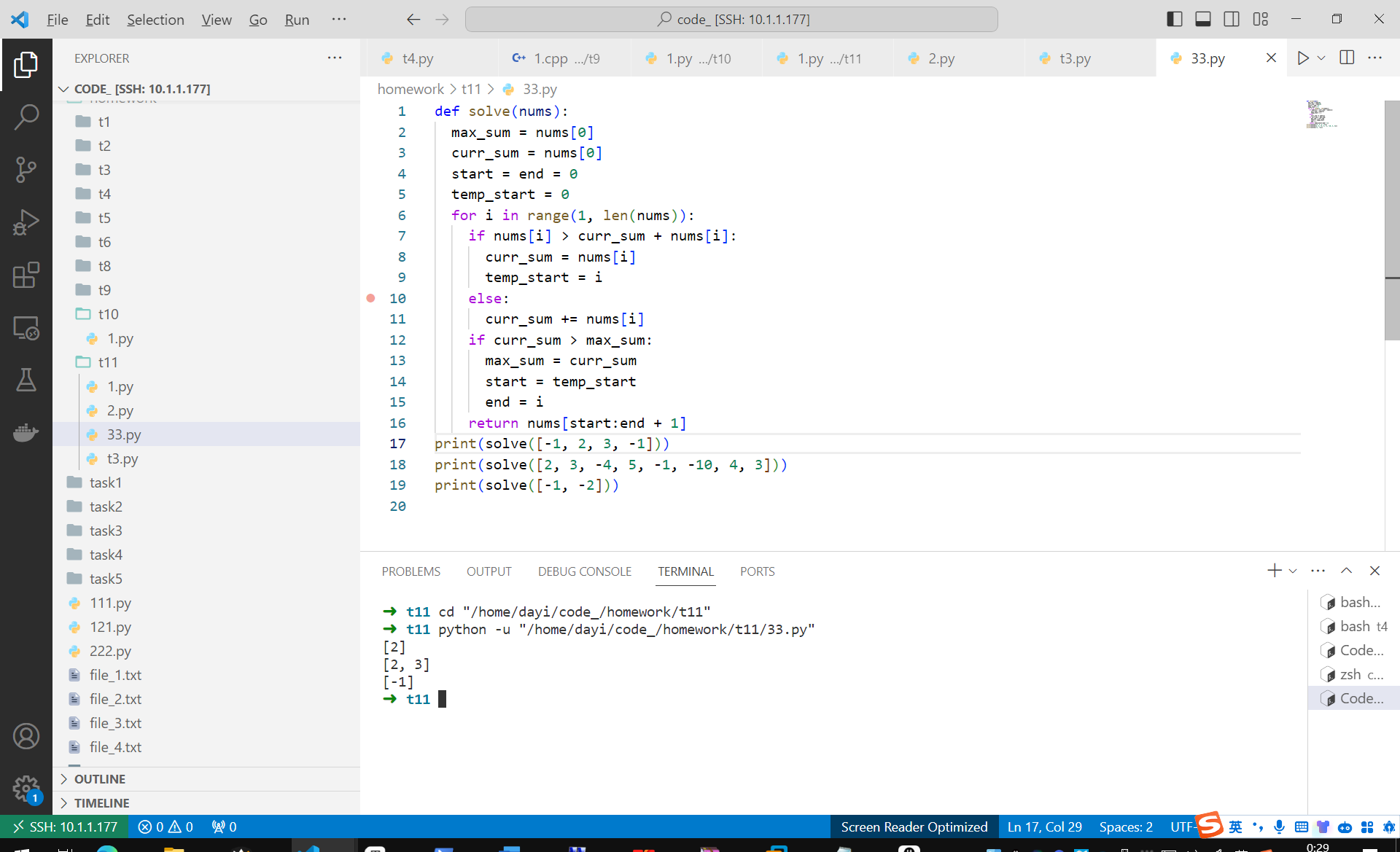
十二 代码下载：

https://p.dabbit.net/blog/pic_bed/sharex/_pn-2023-11-24-15-02-03_Bunny_Lime_Angry.zip
SHA256: 30173e4688c0f01fc77c1be18bb6d5ef0709cd712ee169a396d126a639cfe445

二维码：

文件