算法实验报告3——分支限界法

算法实验报告3——分支限界法

可访问链接：

1. https://type.dayiyi.top/index.php/archives/234/
2. https://www.cnblogs.com/rabbit-dayi/p/17813673.html

1.艰难旅行问题

现已知一个大小为 N · M 的地图，地图中只有可能出现两个数字：0 或 1，
规定如果位于数字为 0 的格子上，则下一步只能往相邻四个格子中数字为 1 的格子走，如果位于数字为 1 的格子上，则下一步只能往相邻四个格子中数字为 0 的格子走。
如果给定起点格子，则可以向上下左右四个方向移动，且同一个格子不能重复走，求能在地图中到达多少格子？

• 兔兔
• 兔兔

我觉得这个题深搜广搜都可以。

DFS

#include<bits/stdc++.h>


const int maxn=2333;
const int maxm=2333;
int mp[maxn][maxm];
int vis[maxn][maxm];
int N,M;

const int dx[] = {0,1,-1,0,0};
const int dy[] = {0,0,0,1,-1};
int dfs(int x,int y){
//  printf("de:%d %d\n",x,y);
  int now = mp[x][y];
  vis[x][y]=1;
  int res = 0;
  res++;
  for(int i =1;i<=4;++i){
    int nx = x+dx[i];
    int ny = y+dy[i];
    if((nx>N)||(ny>M)||(nx<=0)||(ny<=0))continue;
    if((mp[nx][ny]^now )&& (!vis[nx][ny])){
      vis[nx][ny]=1;
      res+=dfs(nx,ny);
    }
  }
  return res;
}

int main(){
  using namespace std;
  cin>>N>>M;
  for(int i=1;i<=N;++i){
    for(int j=1;j<=M;++j){
      cin>>mp[i][j];
    }
  }  
  int st,sy;
  cin>>st>>sy;
  int ans=dfs(st,sy);
  cout<<ans<<"\n";
}

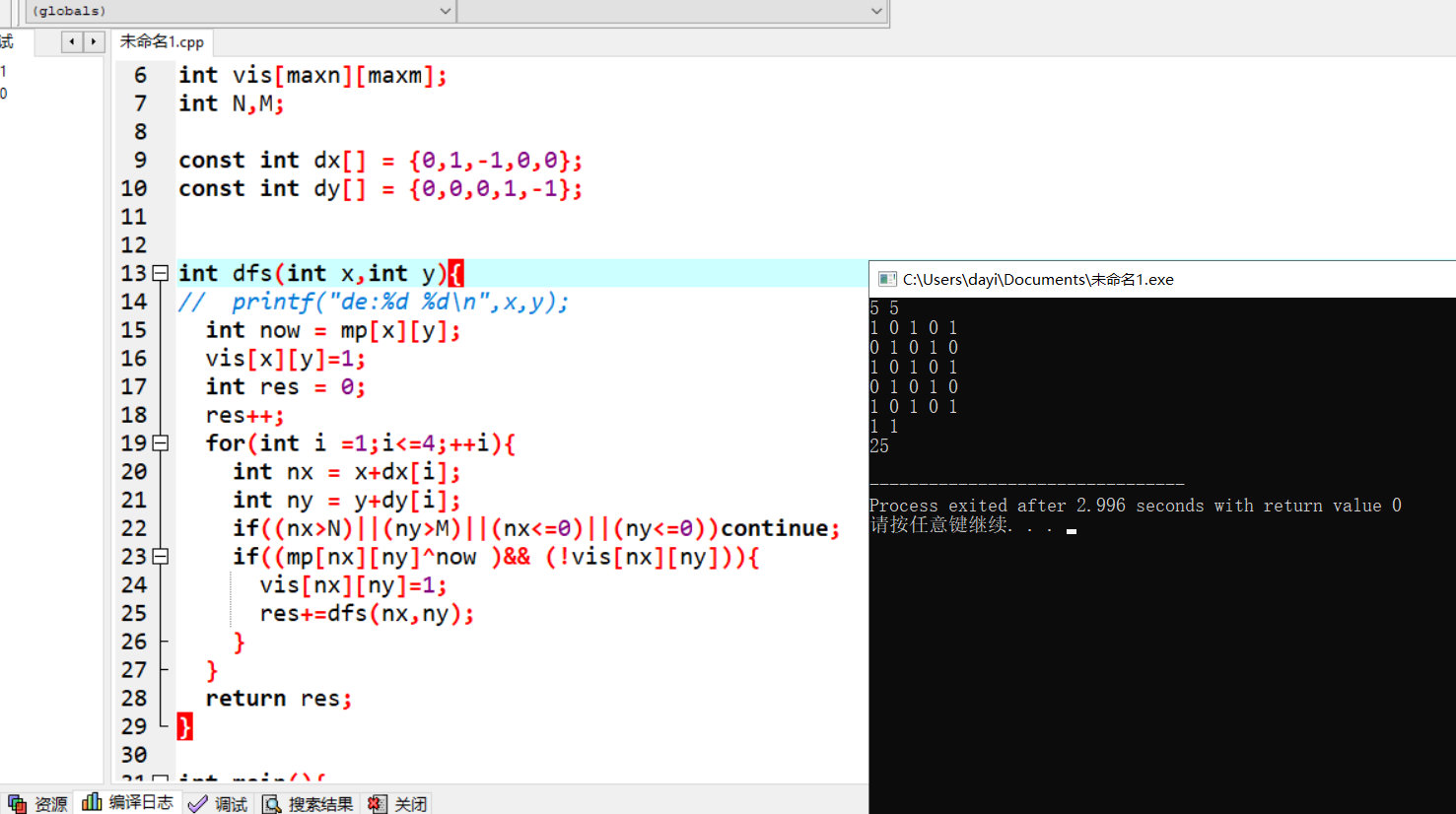
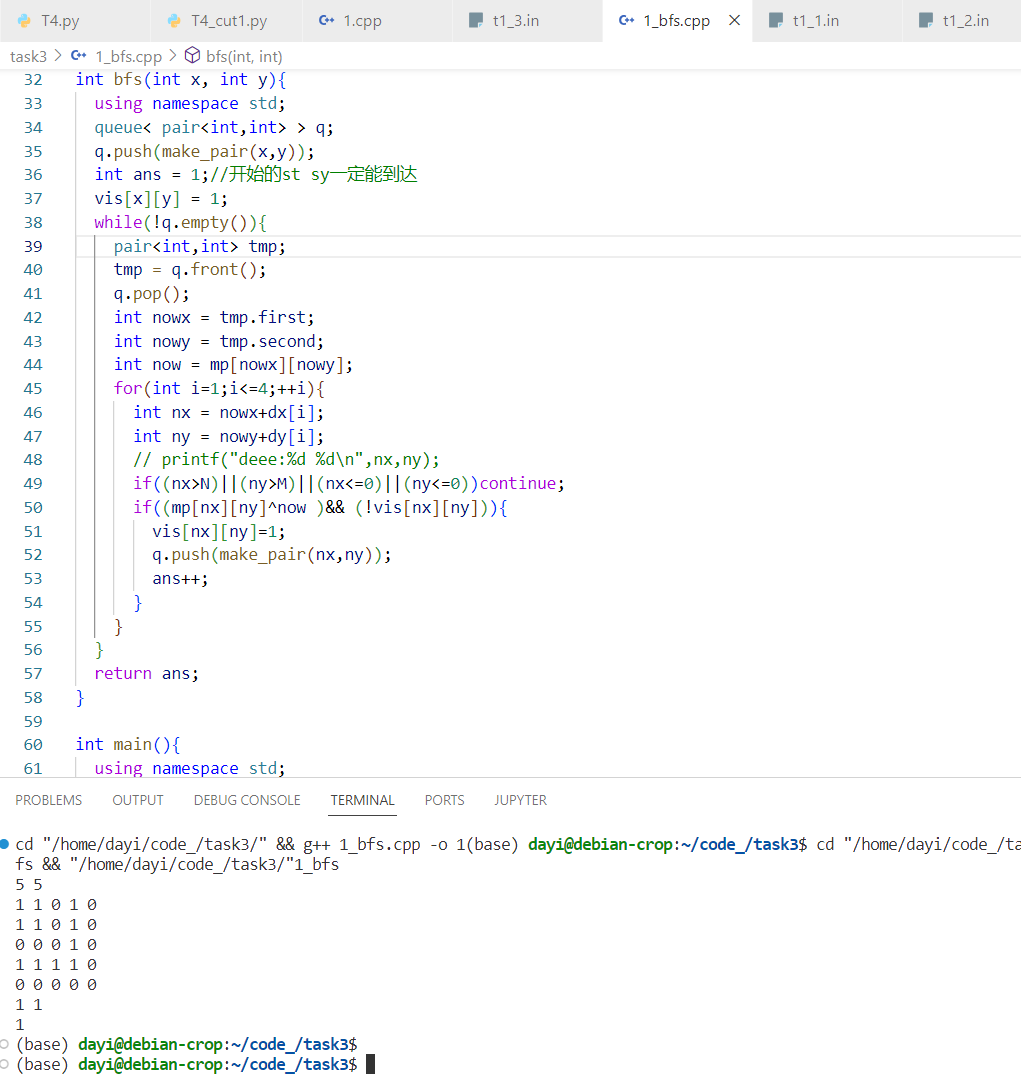
• T1_1.in

5 5 
1 0 1 0 1
0 1 0 1 0
1 0 1 0 1
0 1 0 1 0
1 0 1 0 1
1 1

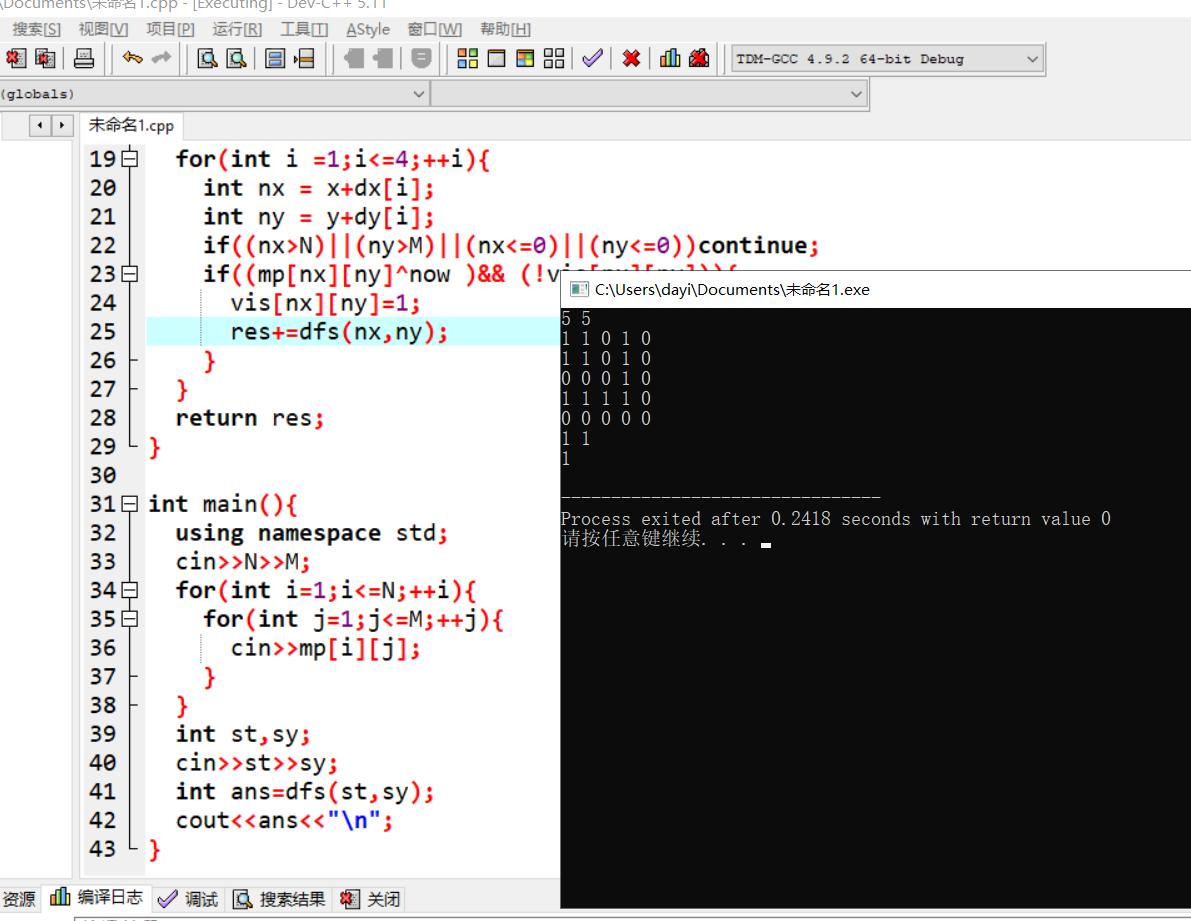
• T1_2.in

5 5
1 1 0 1 0
1 1 0 1 0
0 0 0 1 0
1 1 1 1 0
0 0 0 0 0
1 1

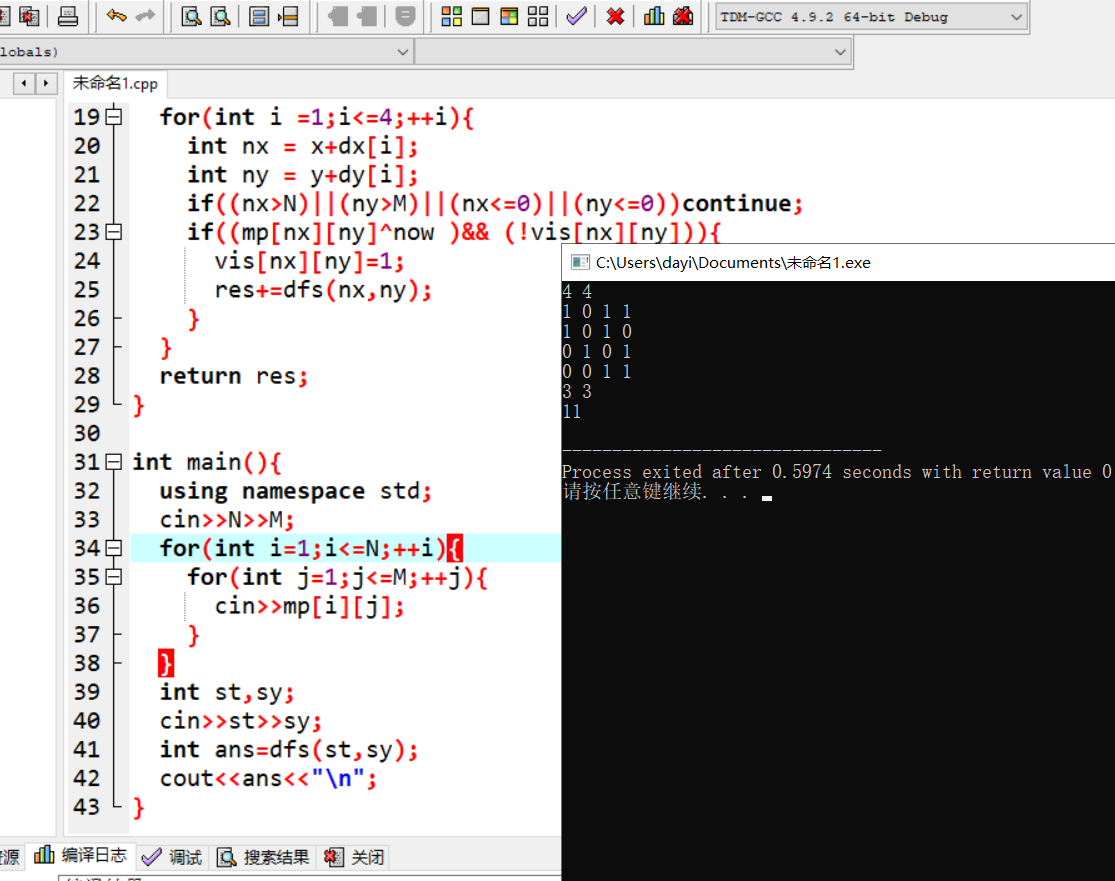
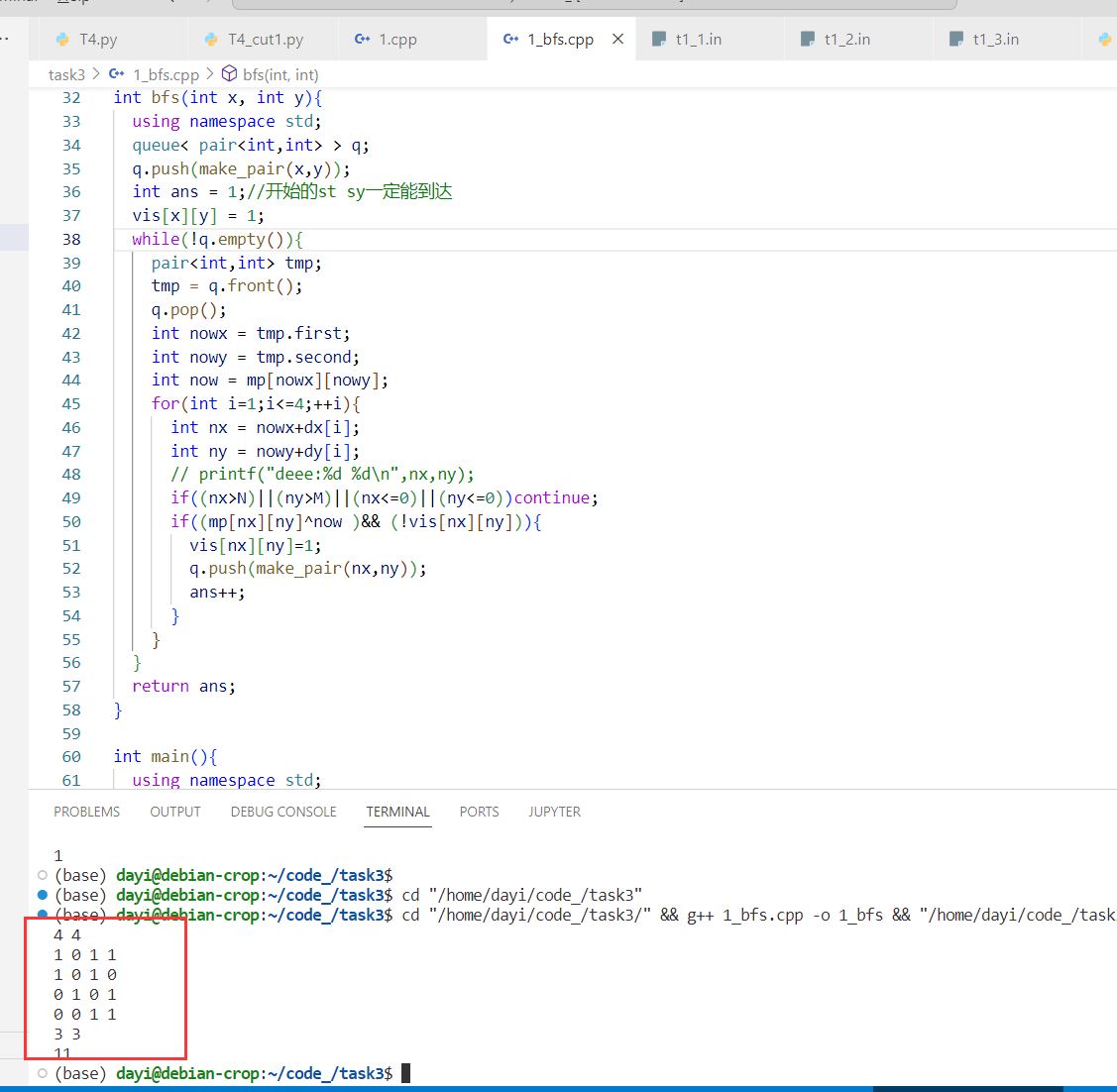
• T1_3.in

4 4
1 0 1 1
1 0 1 0
0 1 0 1
0 0 1 1
3 3

• 样例：

样例1：

样例2：

样例3：

BFS

#include<bits/stdc++.h>

const int maxn=2333;
const int maxm=2333;
int mp[maxn][maxm];
int vis[maxn][maxm];
int N,M;

const int dx[] = {0,1,-1,0,0};
const int dy[] = {0,0,0,1,-1};


int dfs(int x,int y){
//  printf("de:%d %d\n",x,y);
  int now = mp[x][y];
  vis[x][y]=1;
  int res = 0;
  res++;
  for(int i =1;i<=4;++i){
    int nx = x+dx[i];
    int ny = y+dy[i];
    if((nx>N)||(ny>M)||(nx<=0)||(ny<=0))continue;
    if((mp[nx][ny]^now )&& (!vis[nx][ny])){
      vis[nx][ny]=1;
      res+=dfs(nx,ny);
    }
  }
  return res;
}


int bfs(int x, int y){
  using namespace std;
  queue< pair<int,int> > q;
  q.push(make_pair(x,y));
  int ans = 1;//开始的st sy一定能到达
  vis[x][y] = 1;
  while(!q.empty()){
    pair<int,int> tmp;
    tmp = q.front();
    q.pop();
   int nowx = tmp.first;
    int nowy = tmp.second;
    int now = mp[nowx][nowy];
    for(int i=1;i<=4;++i){
      int nx = nowx+dx[i];
      int ny = nowy+dy[i];
      // printf("deee:%d %d\n",nx,ny);
      if((nx>N)||(ny>M)||(nx<=0)||(ny<=0))continue;
      if((mp[nx][ny]^now )&& (!vis[nx][ny])){
        vis[nx][ny]=1;
        q.push(make_pair(nx,ny));
        ans++;
      }
    }
  }
  return ans;
}

int main(){
  using namespace std;
  cin>>N>>M;
  for(int i=1;i<=N;++i){
    for(int j=1;j<=M;++j){
      cin>>mp[i][j];
    }
  }  
  int st,sy;
  cin>>st>>sy;
  int ans=bfs(st,sy);
  cout<<ans<<"\n";
}

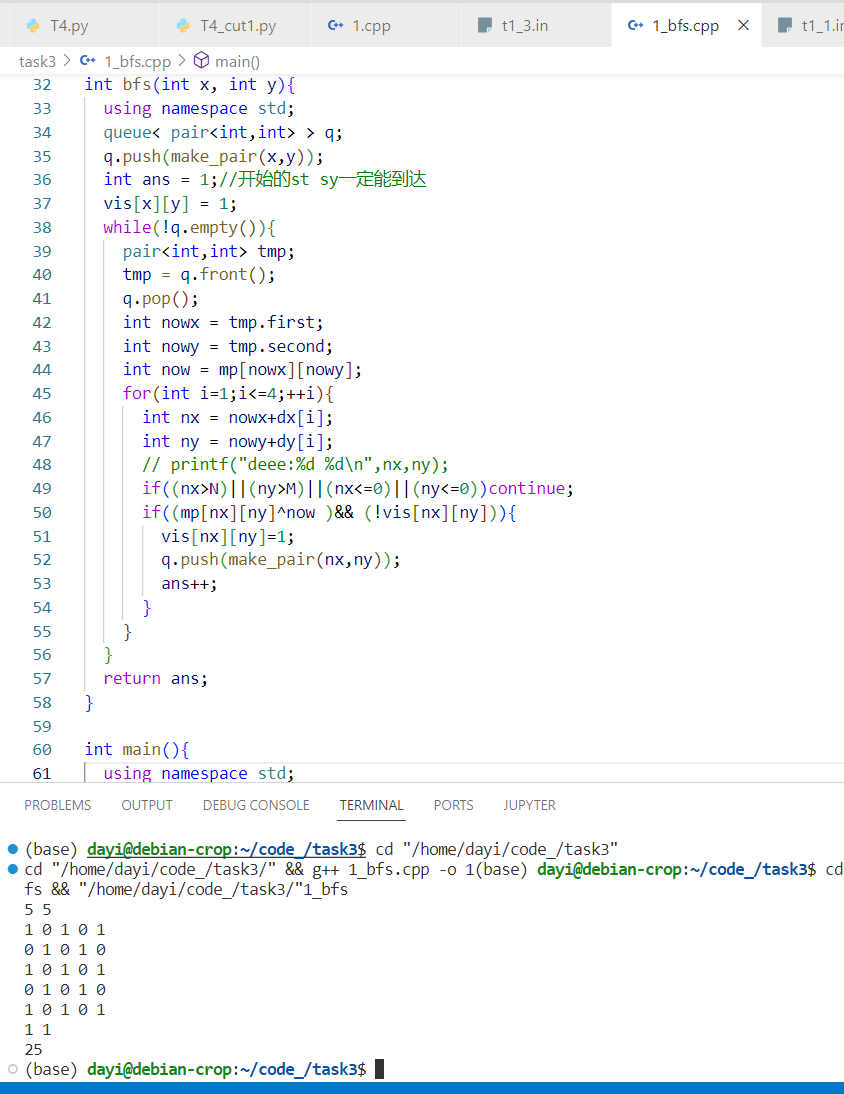
Python 版本：

from collections import deque

maxn = 2333
maxm = 2333
mp = [[0] * maxm for _ in range(maxn)]
vis = [[0] * maxm for _ in range(maxn)]
N, M = 0, 0

dx = [0, 1, -1, 0, 0]
dy = [0, 0, 0, 1, -1]


def dfs(x, y):
    now = mp[x][y]
    vis[x][y] = 1
    res = 1
    for i in range(1, 5):
        nx = x + dx[i]
        ny = y + dy[i]
        if nx > N or ny > M or nx <= 0 or ny <= 0:
            continue
        if mp[nx][ny] != now and not vis[nx][ny]:
            res += dfs(nx, ny)
    return res


def bfs(x, y):
    q = deque()
    q.append((x, y))
    ans = 1 
    vis[x][y] = 1
    while q:
        nowx, nowy = q.popleft()
        now = mp[nowx][nowy]
        for i in range(1, 5):
            nx = nowx + dx[i]
            ny = nowy + dy[i]
            if nx > N or ny > M or nx <= 0 or ny <= 0:
                continue
            if mp[nx][ny] != now and not vis[nx][ny]:
                vis[nx][ny] = 1
                q.append((nx, ny))
                ans += 1
    return ans


def main():
    global N, M
    N, M = map(int, input().split())
    for i in range(1, N + 1):
        mp[i][1:M+1] = list(map(int, input().split()))

    st, sy = map(int, input().split())
    ans = bfs(st, sy)
    print(ans)


if __name__ == "__main__":
    main()

思路和分析

在艰难旅行问题中，我们使用了深度优先搜索（DFS）和广度优先搜索（BFS）两种算法。这两种算法都是通过搜索算法来探索从起点出发可以到达的所有格子。

1. 深度优先搜索（DFS）

• DFS 从起点开始，沿着可能的路径深入探索，直到无法继续为止。然后回溯到上一个分岔点，再沿着另一条路径探索，直到探索所有可能的路径。

• 时间复杂度：DFS 的时间复杂度通常为 \(O(V + E)\)，其中 \(V\) 是顶点数（本问题中为格子数），\(E\) 是边数（本问题中为可能的移动次数）。由于这个问题中，每个格子最多有四个方向可以探索，所以时间复杂度大约是 \(O(4V)\)。

2. 广度优先搜索（BFS）

• BFS 从起点开始，探索所有相邻的格子，然后再探索这些格子的相邻格子，以此类推，直到探索完所有可以到达的格子。
• 时间复杂度：BFS 的时间复杂度也是 \(O(V + E)\)。同样地，由于每个格子最多有四个相邻的格子，所以时间复杂度大约是 \(O(4V)\)。
  BFS 的空间复杂度由队列的最大长度决定，最坏情况下为 \(O(V)\)。

但是在本题中

广度优先搜索速度可能会更快，因为一直递归也是很占用资源的。(虽然占点资源，但我感觉这个题都差不多，没什么区别，队列进出也要消耗资源呀)

2.混乱地铁问题

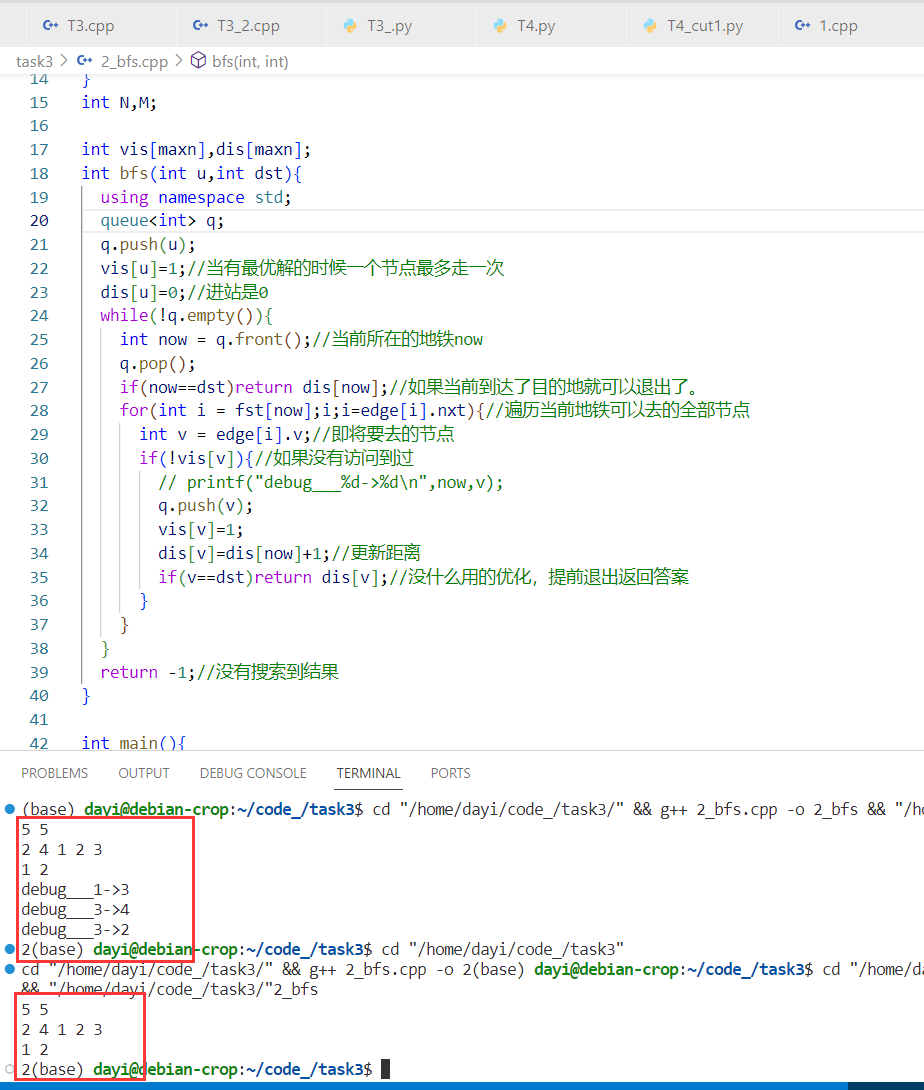
在某一个城市中地铁网极度混乱。一条地铁线路上有 n 个地铁站，分别编号为 1 到 n。地铁线路上的每一个站都会停靠地铁，每一个地铁站上都有一个数字 m，代表从此站出发乘客必须乘坐的站数。
每个地铁站都有通往两个方向的地铁。因此既可以向编号大的方向前进 m 站，也可以向编号小的方向前进 m 站。但如果前进后超出了地铁站的范围，则该地铁不可被乘坐。例如编号为 1 的地铁上的数字为 3，那么在该地铁站上车，可以向正方向坐车到 4 号地铁站。但不能反方向坐车到 -2 号地铁站，因为 -2 号地铁站不存在。现在乘客从 A 号地铁站出发，想要到达 B 号地铁站，求他能否到达，最少要搭乘多少次地铁？

• 每次换乘作为一层深度，需要求出最小的深度，如果在当前层（当前换层次数下）可以有解，那么后面一层的解一定不如当前的好。

• 根据这个性质 BFS 会比 DFS 更先搜索到解，而在这个问题下，我们不需要遍历一整棵搜索树，因此，当搜索到任意一个解的时候，任务完成。

• 可以用邻接表来进行加边。对于 \(i\) 节点可以到达的节点为 \(i-w\) 和 \(i+w\)

  int ww ;cin>>ww;
  if(i-ww>0)addedge(i,i-ww,1);//权值在此题没有意义
  if(i+ww<=N)addedge(i,i+ww,1);
  

C++(c with STL)代码：

#include<bits/stdc++.h>

const int maxn=114514;
const int maxm=12345;
struct edge{
  int u,v,w,nxt;
}edge[maxm<<1];
int fst[maxn];
int cnt;
inline void addedge(int u,int v,int w){
  edge[++cnt].u=u,edge[cnt].v=v,edge[cnt].w=w;
  edge[cnt].nxt=fst[u];
  fst[u]=cnt;
}
int N,M;

int vis[maxn],dis[maxn];
int bfs(int u,int dst){
  using namespace std;
  queue<int> q;
  q.push(u);
  vis[u]=1;//当有最优解的时候一个节点最多走一次
  dis[u]=0;//进站是0
  while(!q.empty()){
    int now = q.front();//当前所在的地铁now
    q.pop();
    if(now==dst)return dis[now];//如果当前到达了目的地就可以退出了。
    for(int i = fst[now];i;i=edge[i].nxt){//遍历当前地铁可以去的全部节点
      int v = edge[i].v;//即将要去的节点
      if(!vis[v]){//如果没有访问到过
        // printf("debug___%d->%d\n",now,v);
        q.push(v);
        vis[v]=1;
        dis[v]=dis[now]+1;//更新距离
        if(v==dst)return dis[v];//没什么用的优化，提前退出返回答案
      }
    }
  }
  return -1;//没有搜索到结果
}

int main(){
  using namespace std;
  cin>>N>>M;
  for(int i=1;i<=N;++i){
    int ww ;cin>>ww;
    if(i-ww>0)addedge(i,i-ww,1);//权值在此题没有意义
    if(i+ww<=N)addedge(i,i+ww,1);
  }
  int st,dt;cin>>st>>dt;
  cout<<bfs(st,dt);
}

Python 版本：

from collections import deque
maxn = 114514
maxm = 12345
class Edge:
  def __init__(self, u=0, v=0, w=0, nxt=0):
    self.u = u
    self.v = v
    self.w = w
    self.nxt = nxt
edges = [Edge() for _ in range(maxm << 1)]
fst = [0] * maxn
cnt = 0
def addedge(u, v, w):
  global cnt, edges, fst
  cnt += 1
  edges[cnt].u = u
  edges[cnt].v = v
  edges[cnt].w = w
  edges[cnt].nxt = fst[u]
  fst[u] = cnt
N, M = 0, 0
vis = [0] * maxn
dis = [0] * maxn
def bfs(u, dst):
  q = deque()
  q.append(u)
  vis[u] = 1
  dis[u] = 0 
  while q:
    now = q.popleft() 
    if now == dst:
        return dis[now] 
    i = fst[now]
    while i:
      v = edges[i].v  
      if not vis[v]:  
        q.append(v)
        vis[v] = 1
        dis[v] = dis[now] + 1 
        if v == dst:
          return dis[v]
      i = edges[i].nxt
  return -1 
def main():
  global N, M
  N, M = map(int, input().split())
  for i in range(1, N + 1):
    ww = int(input())
    if i - ww > 0:
      addedge(i, i - ww, 1)  # The weight has no meaning in this problem
    if i + ww <= N:
      addedge(i, i + ww, 1)
  st, dt = map(int, input().split())
  print(bfs(st, dt))

if __name__ == "__main__":
    main()

混乱地铁问题算法分析

在混乱地铁问题中，我们使用了图的遍历算法（特别是广度优先搜索，BFS）来解决问题。本质上是一个图的遍历问题，其中节点表示地铁站，边表示可行的地铁路线。

广度优先搜索（BFS）

• 从给定的起始节点开始，逐步访问所有可达的节点。在每个节点，算法检查所有相邻的节点，并将那些尚未访问过的节点加入队列中。这个过程持续进行，直到队列为空，即所有可达节点都被访问。
• 时间复杂度：BFS 的时间复杂度通常为 \(O(V + E)\)，其中 \(V\) 是顶点数（本问题中为地铁站数量），\(E\) 是边数（本问题中为可能的地铁线路数量）。每个节点最多被访问一次，每条边最多被检查一次。
• 空间复杂度：最坏情况下为 \(O(V)\)，此题比较固定，最坏情况下队列满载情况。
• BFS 适合用于找到最短路径或者层次遍历的情况，特别是在图的遍历和搜索问题中非常有效。
• 在这个问题中，BFS 通过逐层搜索，能够保证第一次到达终点站的路径是需要最少换乘次数的路径。

3.0-1背包问题

在非空间压缩的基础上（二维 dp 数组），如何反求出我选了什么？

其实挺简单：

• 从 dp[N][M] 开始，逆向查找哪些物品被放入了背包
• 比较 dp[i][j] 与 `dp[i-1][j]`` 是否相等：
• 如果相等，说明第 i 件物品没有被放入背包。
• 如果不相等，说明第 i 件物品被放入了背包，将这个物品记录下来，并将 j 更新为 j-w[i]。
• 将 i 减 1，继续比较。
• 重复这个过程，直到 i 为 0 或者 j 为 0。

具体代码实现：

//反求选了哪几个
int i = N;
int j = W;
for(;i>0&&j>0;i--){
  if(dp[i][j] != dp[i-1][j]){
    res[++cnt]=i;
    j = j-w[i];
  }
}
for(int i=1;i<=cnt;++i){
  printf("sel: %d\n",res[i]);
}

完整 C 语言实现：

#include<iostream>
const int maxn = 1e4+102;
int dp[maxn][maxn];
int w[maxn],v[maxn];
int N,W;


int res[maxn];
int cnt;

int main(){
  using namespace std;
  cin>>N>>W;
  for(int i=1;i<=N;++i){
    cin>>w[i]>>v[i];
  }
  //dp 不装东西的时候假设价值是0
  for(int i=1;i<=N;++i){
    dp[i][0]=0;
  }
  for(int i=1;i<=N;++i){
    for(int j=0;j<=W;++j){
      if(j-w[i]<0)dp[i][j]=dp[i-1][j];
      else dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
    }
  }
  cout<<dp[N][W]<<"\n";

  //反求选了哪几个
  int i = N;
  int j = W;
  for(;i>0&&j>0;i--){
    if(dp[i][j] != dp[i-1][j]){
      res[++cnt]=i;
      j = j-w[i];
    }
  }
  for(int i=1;i<=cnt;++i){
    printf("sel: %d\n",res[i]);
  }
} 

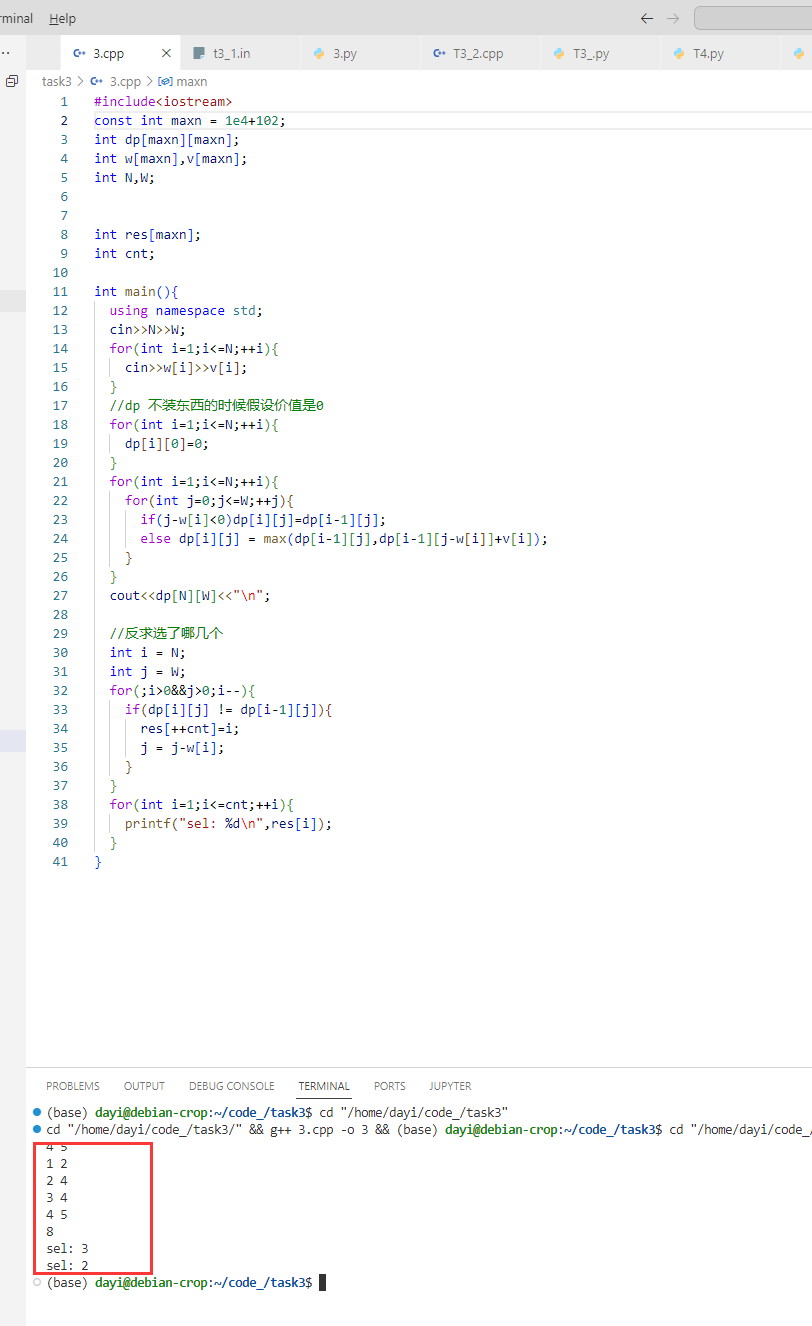
具体的 Python 实现：

def main():
  N, W = map(int, input().split())
  w = [0] * (N + 1)
  v = [0] * (N + 1)
  for i in range(1, N + 1):
    w[i], v[i] = map(int, input().split())

  dp = [[0] * (W + 1) for _ in range(N + 1)]

  for i in range(1, N + 1):
    for j in range(W + 1):
      if j - w[i] < 0:
        dp[i][j] = dp[i - 1][j]
      else:
        dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i])
  print(dp[N][W])
  
  res = []
  i, j = N, W
  while i > 0 and j > 0:
    if dp[i][j] != dp[i - 1][j]:
      res.append(i)
      j -= w[i]
    i -= 1
  for i in range(len(res)):
      print(f"sel: {res[i]}")

if __name__ == "__main__":
    main()

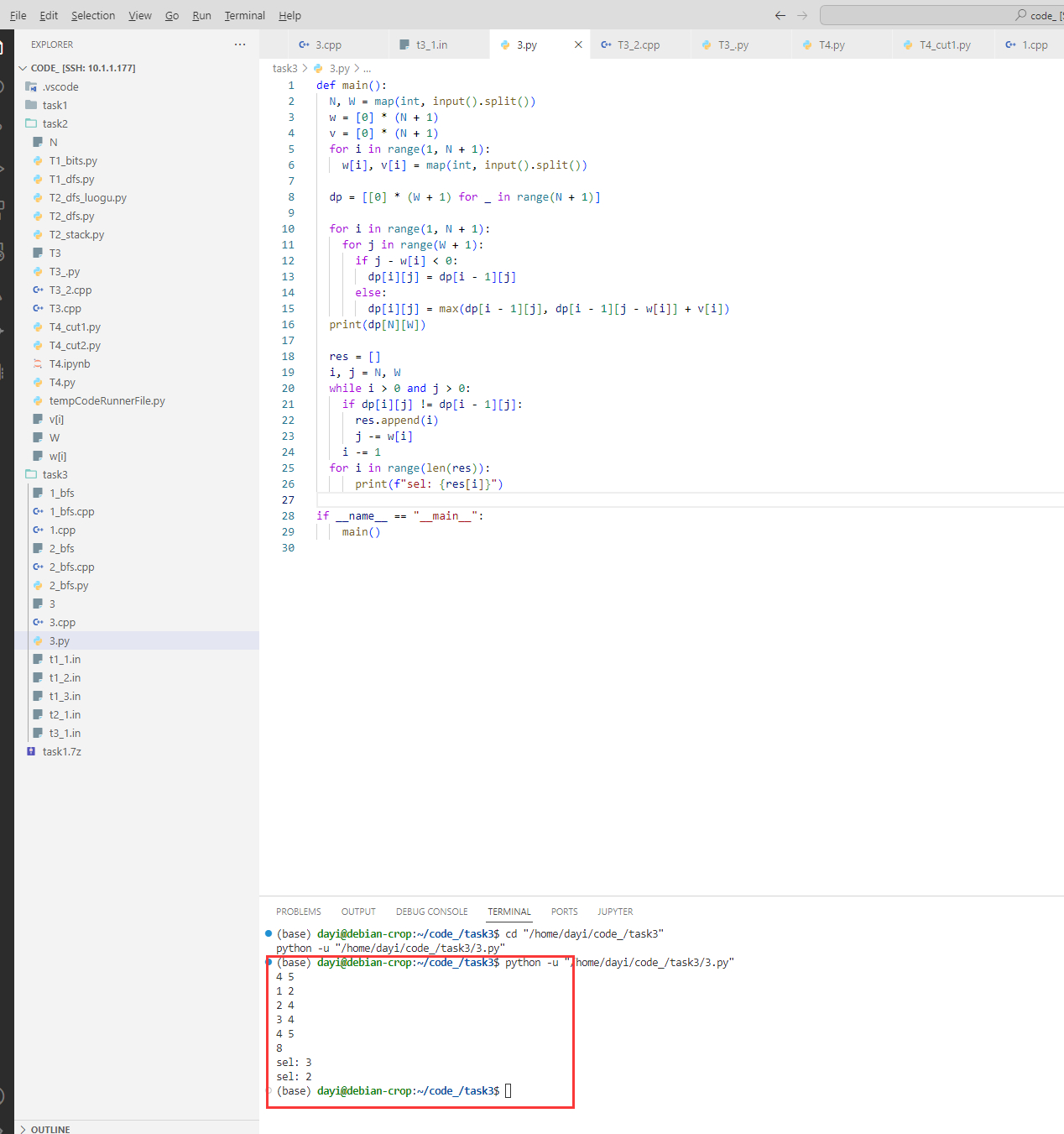
时间复杂度分析

\(O(NW)\) 要dp转移一次的时间复杂度如此。

1. 初始化：从 dp[N][W] 开始，也就是01背包转移完成的DP数组，即考虑所有物品且背包容量为W的情况。
2. 反向追踪：
   • 比较 dp[i][j] 和 dp[i-1][j]。
   • 如果 dp[i][j] != dp[i-1][j]，说明第i件物品被选取，记录该物品，并更新 j 为 j - w[i]（减去该物品的重量）。
   • 重复这个过程，直到 i 或 j 为0。

• 追踪过程的时间复杂度为 \(O(NW+N)\)，其中 \(N\) 是物品数量。因为最多需要追踪 \(N\) 次，每次追踪的操作是常数级别的。
• 反求\(O(N)\) 转移：\(O(NW)\) 合并：\(O(NW+N)\)
• 最坏情况下为 \(O(WN)\)

4.P120 第2题

已知一个 N·M 的国际象棋棋盘，现给定一个起始点、终点。若在起始点上有一个马，
问：从起始点出发，马能否到达终点，到终点最少需要走几步？
输入中包含棋盘的大小、起始点坐标、终点坐标。（马走“日”字。）

这个 比较神奇，它可以走日字：

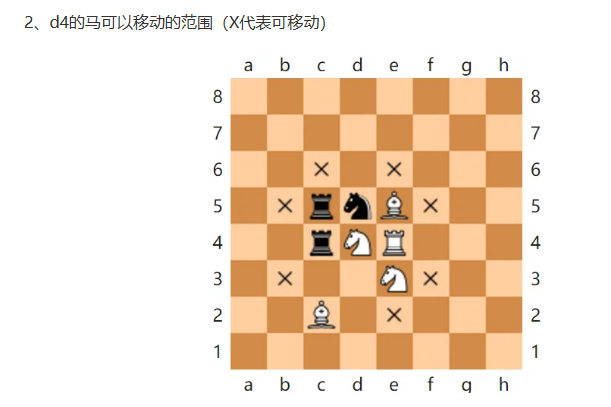
于是找到了个差不多的题目。

https://www.luogu.com.cn/problem/P1443

• 因为求的是最少走多少步，我们在当前的状态里可以求得答案的话，那么下层状态求的一定是更多的数量。
• 这个性质直接用 BFS 就可以啦

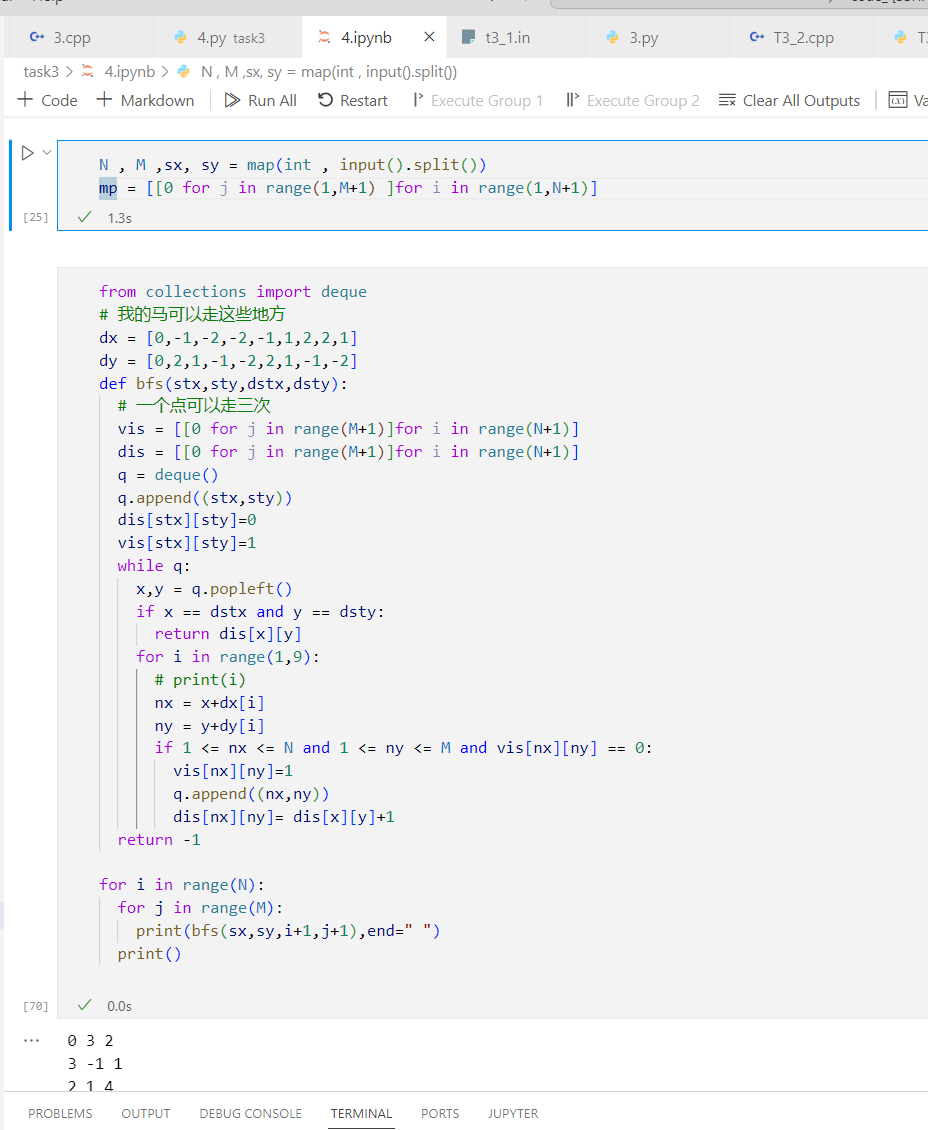
N , M ,sx, sy = map(int , input().split())
mp = [[0 for j in range(1,M+1) ]for i in range(1,N+1)]
from collections import deque
# 我的马可以走这些地方
dx = [0,-1,-2,-2,-1,1,2,2,1]
dy = [0,2,1,-1,-2,2,1,-1,-2]
def bfs(stx,sty,dstx,dsty):
  # 一个点可以走三次
  vis = [[0 for j in range(M+1)]for i in range(N+1)]
  dis = [[0 for j in range(M+1)]for i in range(N+1)]
  q = deque()
  q.append((stx,sty))
  dis[stx][sty]=0
  vis[stx][sty]=1
  while q:
    x,y = q.popleft()
    if x == dstx and y == dsty:
      return dis[x][y]
    for i in range(1,9):
      # print(i)
      nx = x+dx[i]
      ny = y+dy[i]
      if 1 <= nx <= N and 1 <= ny <= M and vis[nx][ny] == 0:
        vis[nx][ny]=1
        q.append((nx,ny))
        dis[nx][ny]= dis[x][y]+1
  return -1

for i in range(N):
  for j in range(M):
    print(bfs(sx,sy,i+1,j+1),end=" ")
  print()

虽然没过，试一试 C++

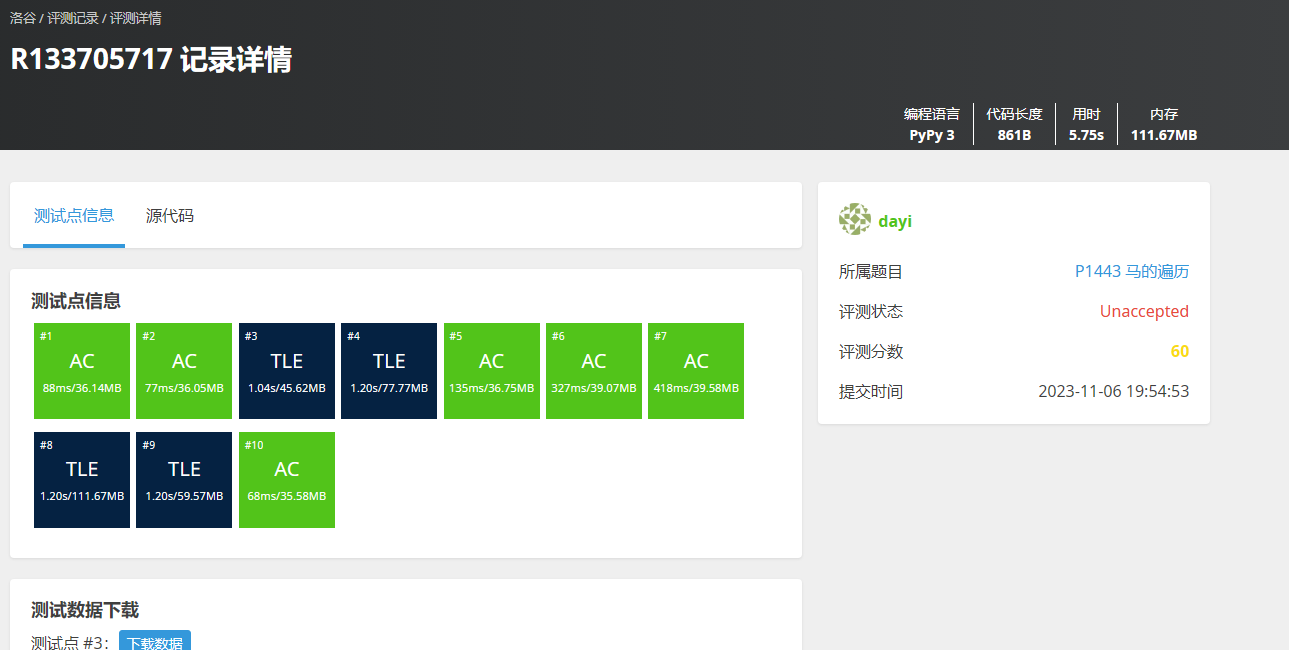
用c++试一试：

#include<bits/stdc++.h>

const int maxn = 2333;
const int maxm = 2333;
int dx[] = {0,-1,-2,-2,-1,1,2,2,1};
int dy[] = {0,2,1,-1,-2,2,1,-1,-2};
int N,M;
int vis[maxn][maxm];
int dis[maxn][maxm];
#define rep(i,x,y) for(int i=x;i<=y;++i)

inline void clear(){
  rep(i,1,N){
    rep(j,1,M){
      vis[i][j]=0;
      dis[i][j]=0;
    }
  }
}

inline int bfs(int stx,int sty,int dstx,int dsty){
  using namespace std;
  queue<pair<int, int>> q;
  clear();
  q.push({stx, sty});
  vis[stx][sty] = 1;
  while (!q.empty()) {
    int x = q.front().first;
    int y = q.front().second;
    q.pop();
    if(x==dstx&&y==dsty){
      return dis[dstx][dsty];
    }
    for(int i=1;i<=8;++i){
      int nx = x+dx[i];
      int ny = y+dy[i];
      if (nx >= 1 && nx <= N && ny >= 1 && ny <= M && vis[nx][ny] == 0) {
        vis[nx][ny] = 1;
        q.push({nx, ny});
        dis[nx][ny] = dis[x][y] + 1;
      }
    }
  }
  return -1;
}
int main(){
  int sx,sy;
  std::cin>>N>>M>>sx>>sy;
  rep(i,1,N){
    rep(j,1,M){
      std::cout<<bfs(sx,sy,i,j)<<" ";
    }
    std::cout<<"\n";
  }
}

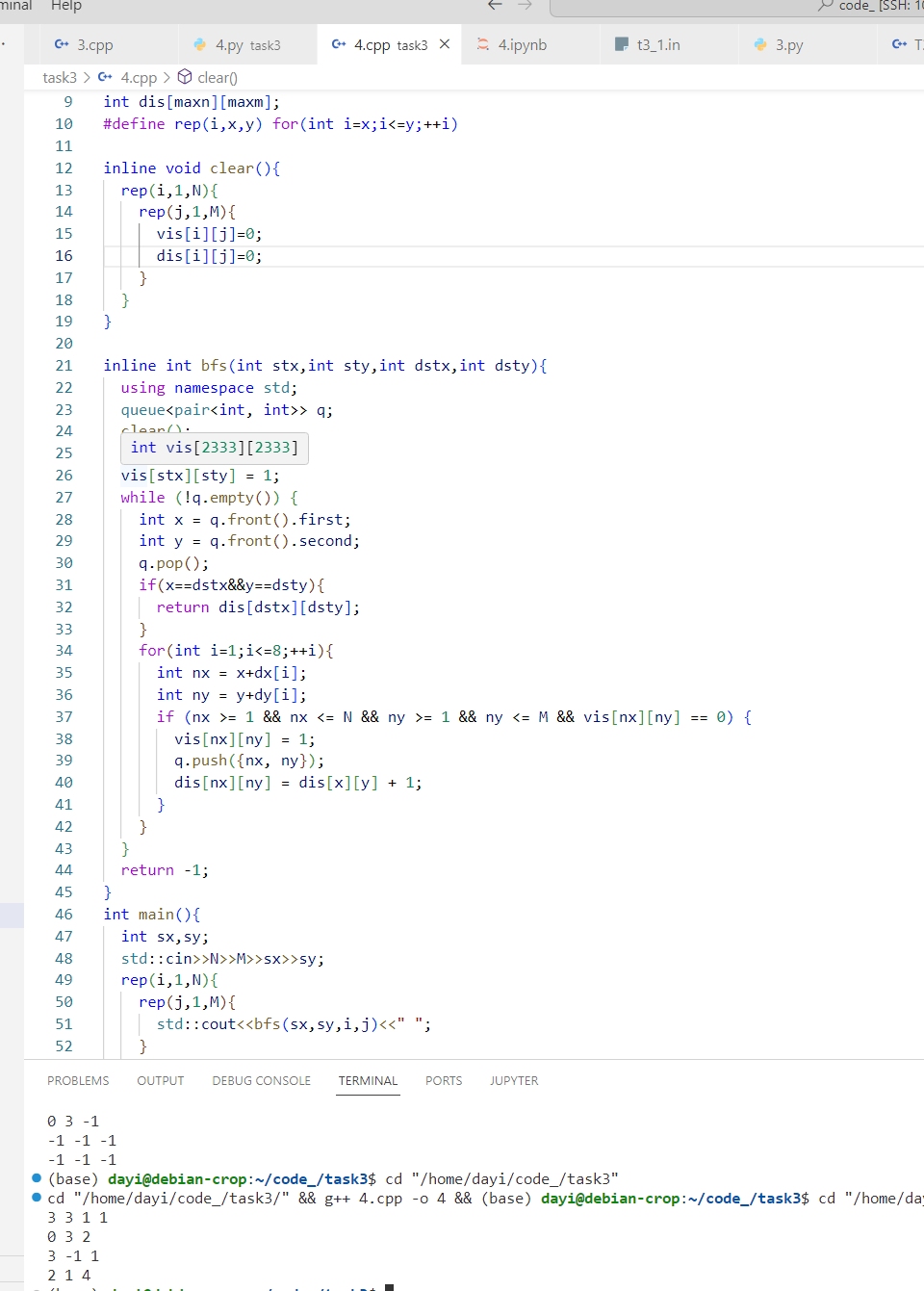
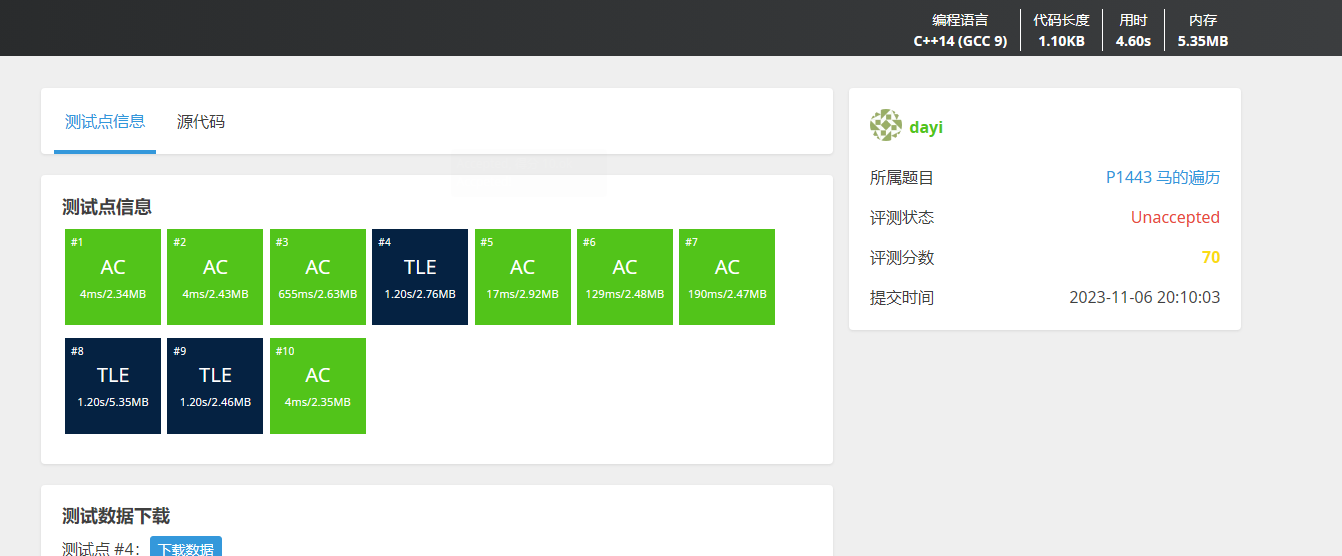
想了想，对于这个题，目标其实不变。所以不用 BFS 多次，BFS 一次就行：

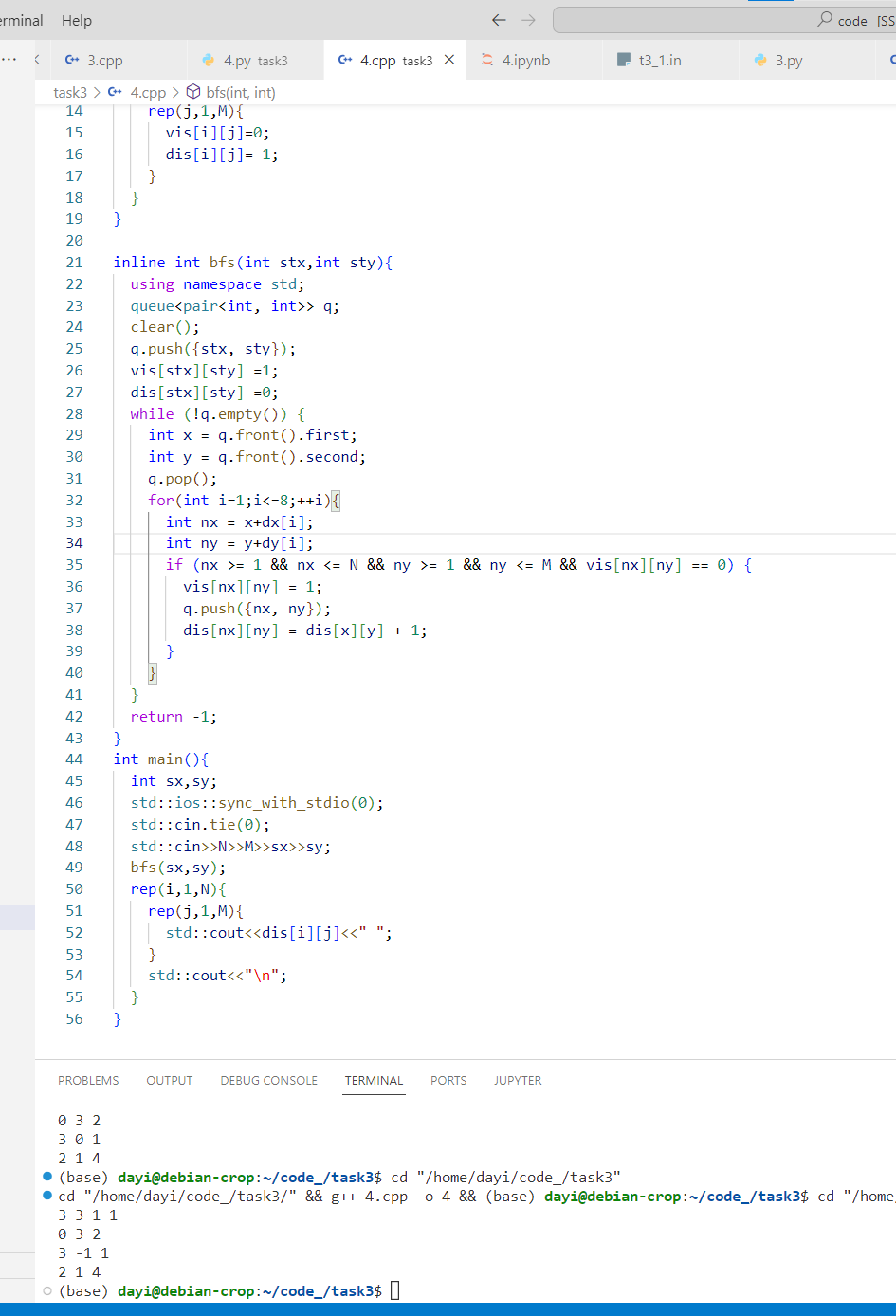
C++

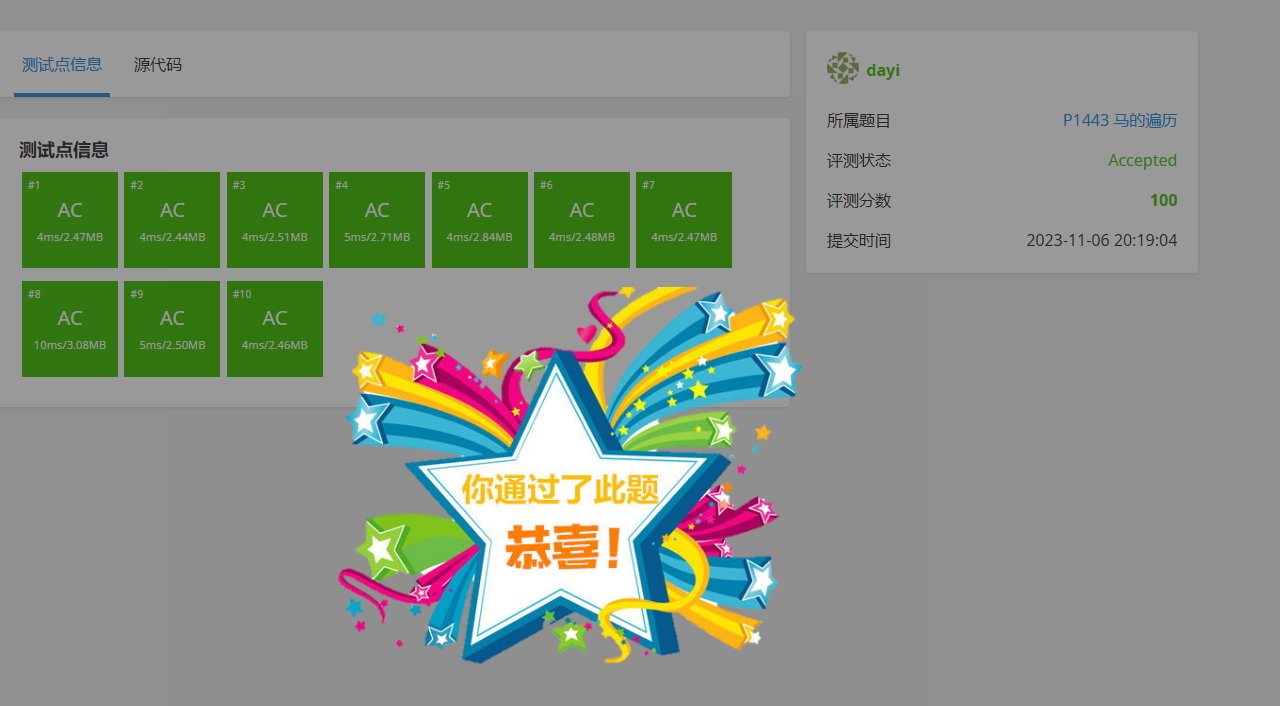
Python

错怪 Python 了

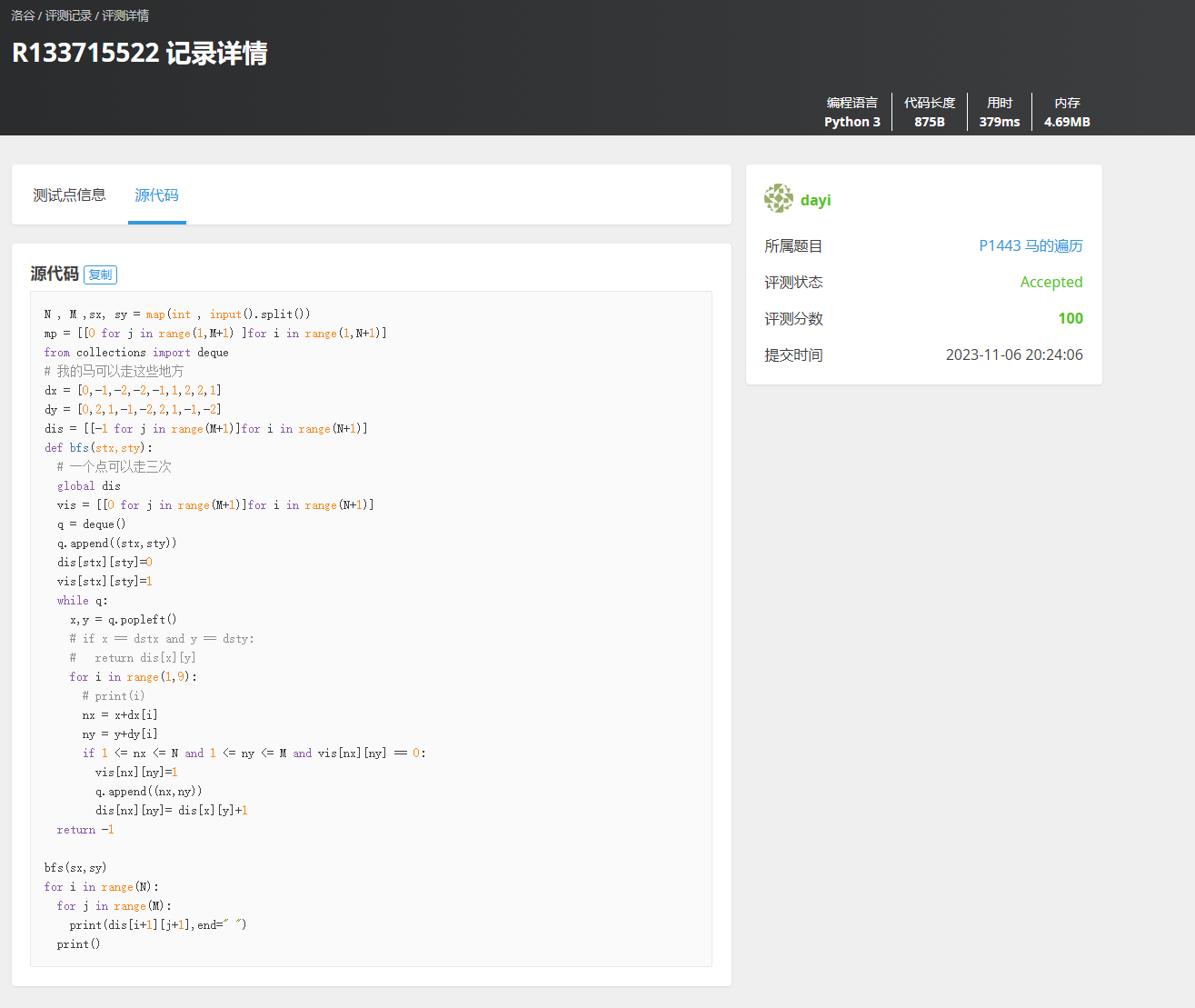
最后的代码

C++

#include<bits/stdc++.h>

const int maxn = 800;
const int maxm = 800;
int dx[] = {0,-1,-2,-2,-1,1,2,2,1};
int dy[] = {0,2,1,-1,-2,2,1,-1,-2};
int N,M;
int vis[maxn][maxm];
int dis[maxn][maxm];
#define rep(i,x,y) for(int i=x;i<=y;++i)

inline void clear(){
  rep(i,1,N){
    rep(j,1,M){
      vis[i][j]=0;
      dis[i][j]=-1;
    }
  }
}

inline int bfs(int stx,int sty){
  using namespace std;
  queue<pair<int, int>> q;
  clear();
  q.push({stx, sty});
  vis[stx][sty] =1;
  dis[stx][sty] =0;
  while (!q.empty()) {
    int x = q.front().first;
    int y = q.front().second;
    q.pop();
    for(int i=1;i<=8;++i){
      int nx = x+dx[i];
      int ny = y+dy[i];
      if (nx >= 1 && nx <= N && ny >= 1 && ny <= M && vis[nx][ny] == 0) {
        vis[nx][ny] = 1;
        q.push({nx, ny});
        dis[nx][ny] = dis[x][y] + 1;
      }
    }
  }
  return -1;
}
int main(){
  int sx,sy;
  std::ios::sync_with_stdio(0);
  std::cin.tie(0);
  std::cin>>N>>M>>sx>>sy;
  bfs(sx,sy);
  rep(i,1,N){
    rep(j,1,M){
      std::cout<<dis[i][j]<<" ";
    }
    std::cout<<"\n";
  }
}

python:

N , M ,sx, sy = map(int , input().split())
mp = [[0 for j in range(1,M+1) ]for i in range(1,N+1)]
from collections import deque
# 我的马可以走这些地方
dx = [0,-1,-2,-2,-1,1,2,2,1]
dy = [0,2,1,-1,-2,2,1,-1,-2]
dis = [[-1 for j in range(M+1)]for i in range(N+1)]
def bfs(stx,sty):
  # 一个点可以走三次
  global dis
  vis = [[0 for j in range(M+1)]for i in range(N+1)]
  q = deque()
  q.append((stx,sty))
  dis[stx][sty]=0
  vis[stx][sty]=1
  while q:
    x,y = q.popleft()
    # if x == dstx and y == dsty:
    #   return dis[x][y]
    for i in range(1,9):
      # print(i)
      nx = x+dx[i]
      ny = y+dy[i]
      if 1 <= nx <= N and 1 <= ny <= M and vis[nx][ny] == 0:
        vis[nx][ny]=1
        q.append((nx,ny))
        dis[nx][ny]= dis[x][y]+1
  return -1

bfs(sx,sy)
for i in range(N):
  for j in range(M):
    print(dis[i+1][j+1],end=" ")
  print()

算法分析

分析：马在国际象棋棋盘上的移动问题

通过广度优先搜索（BFS）算法来解决。BFS 适用于在图中找到从起点到终点的最短路径的问题。在这个特定的问题中，我们需要找到马从起点到终点的最少步数。

算法步骤

1. 初始化：

   • 创建一个队列用于存储每一步马可以到达的位置。
   • 定义一个二维数组 dis 用于存储从起点到每个点的距离，初始值为 -1。
   • 将起始点放入队列，并将该点的 dis 值设置为0。

2. BFS遍历：

   • 当队列不为空时，取出队列的首个元素（当前位置）。
   • 遍历马可能的下一步移动（8个可能的方向）。
   • 如果下一步的位置在棋盘上并且尚未访问过（dis 值为 -1），则：
     • 将该位置加入队列。
     • 更新该位置的 dis 值为当前位置的 dis 值加1。

3. 输出结果：

   • dis 数组就是从起点到每个点的最短距离，即马到达每个位置所需的最少步数。

时空复杂度

• BFS 的时间复杂度为 \(O(V + E)\)，其中 \(V\) 是顶点数（在这个问题中是棋盘上的格子数），\(E\) 是边数（在这个问题中是马可能的移动步数）。

• 在这个问题中，棋盘的大小是 \(N \times M\)，所以顶点数 \(V = NM\)，每个顶点有最多8个可能的移动方向，所以边数 \(E \approx 8NM\)。

• 因此，时间复杂度大致为 \(O(NM)\)。

• 主要的空间消耗来自于存储棋盘上每个点的 dis 值的二维数组和队列，因此空间复杂度为 \(O(NM)\)。

二、总结

都是简单的搜索题啦OVO。

1. 艰难旅行问题

• 问题描述：在一个 N×M 的地图上，根据格子上的数字决定移动方向，求能在地图中到达多少格子。
• 使用了 DFS 和 BFS 算法。
• 分析：DFS 和 BFS 都能有效解决问题。BFS 更适合于找到最大可达区域，因为它按层次遍历，不会因为深度太大而受限。

2. 混乱地铁问题

• 问题描述：在一个混乱的地铁系统中，求从一站到另一站是否可达，如果可达，求最少需要搭乘多少次地铁。
• 分析：BFS 适合此问题，因为它能保证找到的是最短路径。当搜索到解的时候就是答案啦。

3. 0-1 背包问题

• 经典的DP例题

4. 马在国际象棋棋盘上的移动问题

• 问题描述：在一个 N×M 的国际象棋棋盘上，求马从一个点到另一个点的最少移动步数。
• 分析：BFS 适合此问题，因为它能确保找到的路径是最短的。通过一层层的搜索，我们可以找到马到达每个位置所需的最少步数。当搜索到解的时候就是答案啦。

总体分析

• BFS 和 DFS：这两种搜索算法在探索路径和找到特定目标方面非常有效。BFS 通常用于找到最短路径或最大可达区域，而 DFS 更适用于需要深入探索的问题。
• 动态规划：DP 是解决优化问题的强大工具，特别是在处理具有重叠子问题和最优子结构的问题时。

每种算法都有其适用场景和优势。在解决实际问题时，选择合适的算法至关重要。