CH5105 Cookies （线性dp）

传送门

解题思路:

　　贪心的想，贪婪值越大的孩子应该分得更多的饼干，那么先sort一遍在此基础上进行dp。最直观的方向，可以设dp[i][j]为前i个孩子一共分得j块饼干的怨恨最小值。然后转移第i+1个孩子的状态，设a[i]为比第i个孩子拿到更多饼干的孩子的个数，这时会出现两种情况：

　　1.第i+1个孩子获得的饼干比第i个孩子少，那么a[i+1]=i

　　2.第i+1个孩子获得了跟第i个孩子一样多的饼干，那么我们还要找i前面有多少个和i获得同样多的饼干的孩子个数，然后再求出a[i+1]

显而易见第二种情况会大大增加时间复杂度，那么先画个图找找出路

 

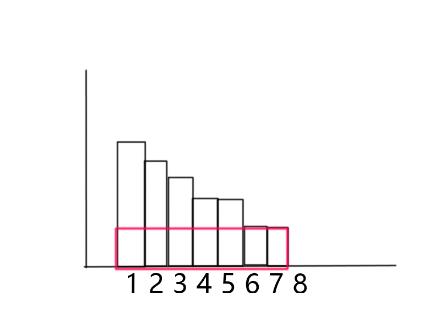
从图上的红框可以看出所有的孩子每人删掉同样多的饼干结果不变。那么获得一条状态转移:dp[i][j]=min(dp[i][j],dp[i][j-i])

同样从上一张图看，若第i个孩子得到了一块饼干，可以通过枚举他前面第k个孩子同样得到1个饼干，得到第二个的状态转移:

　　　dp[i][j]=min(dp[i][j],dp[k][j-(i-k)]+k*(i到i-k的贪婪值之和))

#include<bits/stdc++.h>
using namespace std;
const int maxn=5e3+10;
struct node
{
    int a,id;
}q[55];
bool cmp(node a,node b)
{
    return a.a>b.a;
}
long long dp[51][maxn];
struct no
{
    int i,j;
}g[51][maxn];
long long sum[51],ans[51],r;int n,m;
void print(int i,int j)
{
    if(i==0)    return;
    print(g[i][j].i,g[i][j].j);
    if(g[i][j].i==i)for(int h=1;h<=i;h++)ans[q[h].id]++;
    else for(int h=g[i][j].i+1;h<=i;h++)ans[q[h].id]=1;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)    scanf("%d",&q[i].a),q[i].id=i;
    memset(dp,0x3f,sizeof dp);
    dp[0][0]=0;
    sort(q+1,q+1+n,cmp);
    for(int i=1;i<=n;i++)    sum[i]=sum[i-1]+q[i].a;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(j-i>=0&&dp[i][j]>dp[i][j-i]){
                dp[i][j]=dp[i][j-i];
                g[i][j].i=i;g[i][j].j=j-i;
            }
            for(int k=0;k<i;k++){
                if(j-(i-k)>=0&&dp[i][j]>dp[k][j-(i-k)]+1LL*k*(sum[i]-sum[k])){
                    dp[i][j]=dp[k][j-(i-k)]+k*(sum[i]-sum[k]);
                    g[i][j].i=k;g[i][j].j=j-(i-k);
                }
            }
        }
    }
    cout<<dp[n][m]<<endl;
    print(n,m);
    for(int i=1;i<=n;i++)
        printf("%d%c",ans[i],i==n?'\n':' ');
}