模板-选择最少的区间数目可以覆盖连续区间[0,n]
方法:
首先建立一个一维数组nums, nums[i] 表是在当前位置上还能向右跑几步;
然后更新最右距离:
// nums 最优距离数组 // t 要跳的位置 public int jump(int[] nums, int t) { int n = nums.length; if(n==1){ return 0; } int mr = 0; // 能跳的最右边的位置 int ans = 0; // 跳的次数 int end = 0; // 上一次跳的最右边位置 for (int i = 0; i < n; i++) { if(i>mr) { return -1; } mr = Math.max(mr, nums[i]+i); if(mr>t){ return ans+1; } if(end == i){ end = mr; ans++; } } return ans; }
例题1、
55. 跳跃游戏
nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4] 输出:true 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4] 输出:false 解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
解题思路:
如果某一个作为 起跳点 的格子可以跳跃的距离是 3,那么表示后面 3 个格子都可以作为 起跳点
可以对每一个能作为 起跳点 的格子都尝试跳一次,把 能跳到最远的距离 不断更新
如果可以一直跳到最后,就成功了
这种方法所依据的核心特性:如果一个位置能够到达,那么这个位置左侧所有位置都能到达。 想到这一点,解法就呼之欲出了~
这里只需要判断能不能跳到n-1 就行,不需要ans;
class Solution { public boolean canJump(int[] nums) { int n = nums.length; if(n==1){ return true; } int mr = 0, ans = 0, pre = 0; for (int i = 0; i < n; i++) { if(i>mr) { return false; } mr = Math.max(mr, nums[i]+i); } return true; } }
45. 跳跃游戏 II
n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是2。 从下标为 0 跳到下标为 1 的位置,跳1步,然后跳3步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4] 输出: 2
taoy
class Solution { public int jump(int[] nums) { int n = nums.length; if(n==1){ return 0; } int mr = 0, ans = 0, end = 0; for (int i = 0; i < n; i++) { if(i>mr) { return -1; } mr = Math.max(mr, nums[i]+i); if(mr>=n-1){ return ans+1; } if(end == i){ end = mr; ans++; } } return ans; } }
你将会获得一系列视频片段,这些片段来自于一项持续时长为 time 秒的体育赛事。这些片段可能有所重叠,也可能长度不一。
使用数组 clips 描述所有的视频片段,其中 clips[i] = [starti, endi]表示:某个视频片段开始于 starti 并于 endi 结束。
甚至可以对这些片段自由地再剪辑:
- 例如,片段
[0, 7]可以剪切成[0, 1] + [1, 3] + [3, 7]三部分。
我们需要将这些片段进行再剪辑,并将剪辑后的内容拼接成覆盖整个运动过程的片段([0, time])。返回所需片段的最小数目,如果无法完成该任务,则返回 -1 。
示例 1:
输入:clips = [[0,2],[4,6],[8,10],[1,9],[1,5],[5,9]], time = 10 输出:3 解释: 选中 [0,2], [8,10], [1,9] 这三个片段。 然后,按下面的方案重制比赛片段: 将 [1,9] 再剪辑为 [1,2] + [2,8] + [8,9] 。 现在手上的片段为 [0,2] + [2,8] + [8,10],而这些覆盖了整场比赛 [0, 10]。
示例 2:
输入:clips = [[0,1],[1,2]], time = 5 输出:-1 解释: 无法只用 [0,1] 和 [1,2] 覆盖 [0,5] 的整个过程。
示例 3:
输入:clips = [[0,1],[6,8],[0,2],[5,6],[0,4],[0,3],[6,7],[1,3],[4,7],[1,4],[2,5],[2,6],[3,4],[4,5],[5,7],[6,9]], time = 9 输出:3 解释: 选取片段 [0,4], [4,7] 和 [6,9] 。
class Solution { public int videoStitching(int[][] clips, int time) { int n =0; for(int[] a: clips){ n = Math.max(n, a[1]); } if(time>n){ return -1; } int[] right = new int[n+1]; for(int[] a: clips){ for(int i=a[0];i<a[1];i++){ right[i] = Math.max(a[1]-i,right[i]); } } int ans=0, pre=0, mx=0; for(int i=0; i<n+1; i++){ if(mx <i) { return -1; } mx = Math.max(mx, right[i]+i); if(mx>=time){ return ans+1; } if(pre==i){ pre = mx; ans++; } } return ans; } }
1326. 灌溉花园的最少水龙头数目
n,从点 0 开始,到点 n 结束。花园里总共有 n + 1 个水龙头,分别位于 [0, 1, ..., n] 。
给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ,其中 ranges[i] (下标从 0 开始)表示:如果打开点 i 处的水龙头,可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。
请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方,请你返回 -1 。
示例 1:
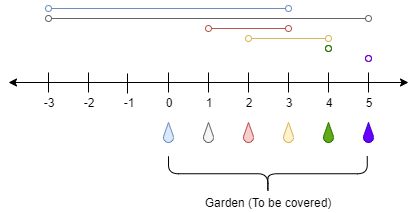
输入:n = 5, ranges = [3,4,1,1,0,0] 输出:1 解释: 点 0 处的水龙头可以灌溉区间 [-3,3] 点 1 处的水龙头可以灌溉区间 [-3,5] 点 2 处的水龙头可以灌溉区间 [1,3] 点 3 处的水龙头可以灌溉区间 [2,4] 点 4 处的水龙头可以灌溉区间 [4,4] 点 5 处的水龙头可以灌溉区间 [5,5] 只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。
示例 2:
输入:n = 3, ranges = [0,0,0,0] 输出:-1 解释:即使打开所有水龙头,你也无法灌溉整个花园。
class Solution { public int minTaps(int n, int[] ranges) { int[] rightMost = new int[n+1]; for(int i=0; i<n+1; i++){ int l = Math.max(0, i-ranges[i]); int r = Math.min(n, i+ranges[i]); for (int j = l; j < r; j++){ rightMost[j] = Math.max(rightMost[j], r); } } int res = 0; // 结果 int right = 0; // 当前最右边节点 int pre = 0; for(int i=0; i<n; i++){ right = Math.max(right, rightMost[i]); if(right<=i){ return -1; } if(pre == i){ pre = right; res+=1; } } return res; } }





