格雷编码

题目描述

n 位格雷码序列 是一个由 2n 个整数组成的序列，其中：

• 每个整数都在范围 [0, 2n - 1] 内（含 0 和 2n - 1）

• 第一个整数是 0

• 一个整数在序列中出现 不超过一次

• 每对 相邻 整数的二进制表示 恰好一位不同 ，且

• 第一个 和 最后一个 整数的二进制表示 恰好一位不同

给你一个整数 n ，返回任一有效的 n 位格雷码序列 。

示例 1：

输入：n = 2
输出：[0,1,3,2]
解释：
[0,1,3,2] 的二进制表示是 [00,01,11,10] 。
- 00 和 01 有一位不同
- 01 和 11 有一位不同
- 11 和 10 有一位不同
- 10 和 00 有一位不同
[0,2,3,1] 也是一个有效的格雷码序列，其二进制表示是 [00,10,11,01] 。
- 00 和 10 有一位不同
- 10 和 11 有一位不同
-11 和 01 有一位不同
- 01 和 00 有一位不同

示例 2：

输入：n = 1
输出：[0,1]

提示：

• 1 <= n <= 16

核心代码

方法一：使用规律

具体方法

下表为0为、1位、2位、3位、4位格雷码的实例，我们可以发现这样一个规律。

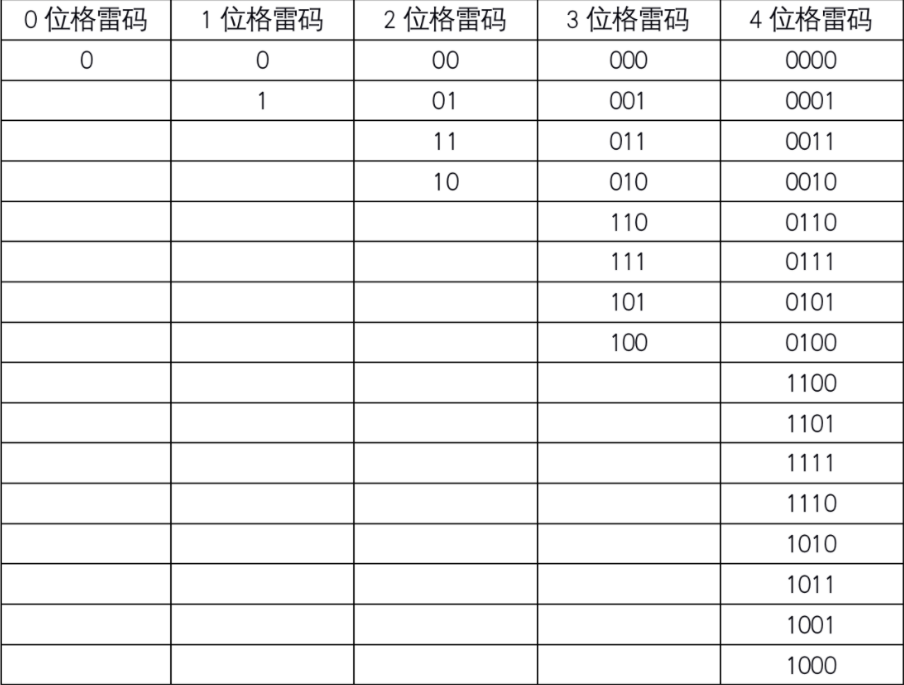
总结规律：

1. 1位格雷码有两个码字
2. (n+1)位格雷码中的前2^n个码字等于n位格雷码的码字，按顺序书写，加前缀0
3. (n+1)位格雷码中的后2^n个码字等于n位格雷码的码字，按逆序书写，加前缀1
4. n+1位格雷码的集合 = n位格雷码集合(顺序)加前缀0 + n位格雷码集合(逆序)加前缀1

根据这个规律就可以直接写代码了。

Java中有三种移位运算符

<<      :     左移运算符，num << 1,相当于num乘以2

>>      :     右移运算符，num >> 1,相当于num除以2

>>>    :     无符号右移，忽略符号位，空位都以0补齐

public List<Integer> grayCode(int n){
        List<Integer> result = new ArrayList<Integer>();
        result.add(0);
        if(n==0){
            return result;
        }
        int first = 1;
        for (int i = 0; i < n; i++) {
            for (int j = result.size()-1; j >= 0; j--) {
                result.add(first + result.get(j));
            }
            first = first << 1;
        }
        return result;
    }

 

 

方法二：二进制码→格雷码

具体方法

此方法从对应的n位二进制码字中直接得到n位格雷码码字，步骤如下：

1. 对n位二进制的码字，从右到左，以0到n-1编号
2. 如果二进制码字的第i位和i+1位相同，则对应的格雷码的第i位为0，否则为1（当i+1=n时，二进制码字的第n位被认为是0，即第n-1位不变）

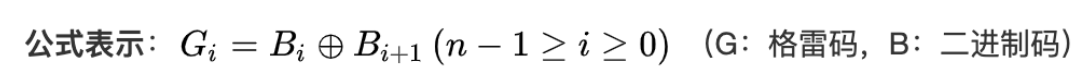
例如：二进制码0101，为4位数，所以其所转为之格雷码也必为4位数，因此可取转成之二进位码第五位为0，即0 b3 b2 b1 b0。

0 xor 0=0，所以g3=0

0 xor 1=1，所以g2=1

1 xor 0=1，所以g1=1

0 xor 1=1，所以g0=1

因此所转换为之格雷码为0111

总结：第n个格雷码 G(n) = n xor (n>>1)

关键是搞清楚格雷编码的生成过程, G(i) = i ^ (i/2);
        如 n = 3: 
        G(0) = 000, 
        G(1) = 1 ^ 0 = 001 ^ 000 = 001
        G(2) = 2 ^ 1 = 010 ^ 001 = 011 
        G(3) = 3 ^ 1 = 011 ^ 001 = 010
        G(4) = 4 ^ 2 = 100 ^ 010 = 110
        G(5) = 5 ^ 2 = 101 ^ 010 = 111
        G(6) = 6 ^ 3 = 110 ^ 011 = 101
        G(7) = 7 ^ 3 = 111 ^ 011 = 100

public List<Integer> grayCode2(int n){
        List<Integer> result = new ArrayList<Integer>();
        result.add(0);
        if(n==0){
            return result;
        }
        for (int i = 1; i < 1<<n; i++) {
            result.add(i^(i>>1));
        }
        return result;
    }

 

方法三：回溯

具体方法

在题解区看到一位老哥分享的，由于格雷码主要是由0或1组成，通过找规律，可以发现其实也可以使用回溯来解决。

规矩使用的是方法一的规律，在递归的时候需要主要数组的顺序是01还是10，看下图n=3的情况。

 

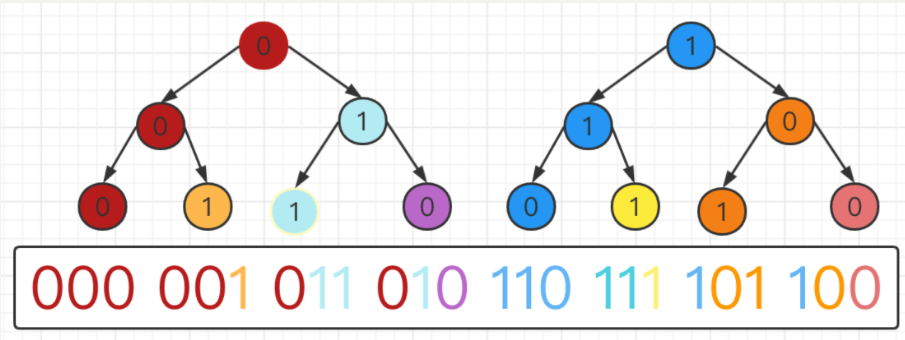
class Solution {
    List<Integer> res = new ArrayList<>();
    public List<Integer> grayCode(int n) {
        dfs(n,new StringBuilder(),new int[]{0,1});
        return res;
    }
    public void dfs(int n, StringBuilder sb, int[] nums){
        //判断条件，是否返回
        if(sb.length() == n){
            // 二进制转换为十进制
            res.add(Integer.valueOf(sb.toString(),2));
            return;
        }
        //回溯第一个状态
       sb.append(nums[0]);
       //注意数组
       dfs(n,sb,new int[]{0,1});
       sb.deleteCharAt(sb.length()-1);
       // 回溯第二个状态
       sb.append(nums[1]);
       //注意数组
       dfs(n,sb,new int[]{1,0});
       sb.deleteCharAt(sb.length()-1);
    }
}

 

 

ps：如果是从某一数字x数字开始，其实只需要生成从0 开始的格雷编码以后，依次和x 进行异或即可