二叉树的右视图

199. 二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

示例 1:

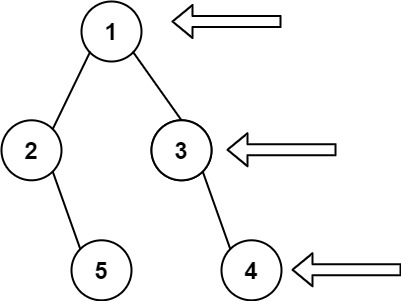
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
示例 2:

输入: [1,null,3]
输出: [1,3]
示例 3:

输入: []
输出: []

 

思路： 我们按照 「根结点 -> 右子树 -> 左子树」 的顺序访问，就可以保证每层都是最先访问最右边的节点的。

 

（与先序遍历 「根结点 -> 左子树 -> 右子树」 正好相反，先序遍历每层最先访问的是最左边的节点）

 

时间复杂度： O(N)O(N)，每个节点都访问了 1 次。
空间复杂度： O(N)O(N)，因为这不是一棵平衡二叉树，二叉树的深度最少是 logNlogN, 最坏的情况下会退化成一条链表，深度就是 NN，因此递归时使用的栈空间是 O(N)O(N) 的。

 

class Solution {
    List<Integer> res = new ArrayList<>();

    public List<Integer> rightSideView(TreeNode root) {
        dfs(root, 0);
        return res;
    }

    public void dfs(TreeNode root, int depth){
        if(root == null){
            return;
        }
13         if(depth == res.size()){
14             res.add(root.val);
15         }
        dfs(root.right, depth+1);
        dfs(root.left, depth+1);
    }
}

 

思考：其实我觉得这道题最有意思的是dfs 怎么计算第一次到达某一层，这里用结果集的大小来保证，很有意思

\

补一个宽度优先搜索：

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        if (root == null){
            return res;
        }
        Deque<TreeNode> q = new LinkedList<>();
        q.add(root);
        int len = 1;
        while(!q.isEmpty()){
            int tem = 0;
            for(int i=0; i<len; i++){
                TreeNode n = q.pollFirst();
                if(n.left !=null){
                    q.add(n.left);
                    tem +=1;
                }
                if(n.right != null){
                    q.add(n.right);
                    tem +=1;
                }
                if(i == len -1){
                    res.add(n.val);
                }
            }
            len = tem;
        }
        return res;
    }
}