二维前缀和

二维前缀和

一维前缀和比较好理解，例如，对于数组 1，2，3，4，5 来说，第k个前缀和为前k个数的和，

即为 ：1，3，6，10，15。

 

什么是二维前缀和呢？

设二维数组的A的大小为m*n，行下标的范围为[1,m]，列范围为[1, n]。数组P是A的前缀和数组，则有：

• 如果 i 和 j 中至少有一个等于 0， 则有P[i][j] 也等于 0。
• 如果 i 和 j 均大于 0，那么 P[i][j] 表示 A 中以 (1, 1) 为左上角，(i, j) 为右下角的矩形区域的元素之和

数组 P 可以帮助我们在 O(1) 的时间内求出任意一个矩形区域的元素之和。具体地，设我们需要求和的矩形区域的左上角为 (x1, y1)，右下角为 (x2, y2)，则该矩形区域的元素之和可以表示为：

sum = A[x1..x2][y1..y2]
= P[x2][y2] - P[x1 - 1][y2] - P[x2][y1 - 1] + P[x1 - 1][y1 - 1]

其正确性可以通过容斥原理得出。以下图为例，当 A 的大小为 8 * 5，需要求和的矩形区域（深绿色部分）的左上角为 (3, 2)，右下角为 (5, 5) 时，该矩形区域的元素之和为 P[5][5] - P[2][5] - P[5][1] + P[2][1]。

 

 

 

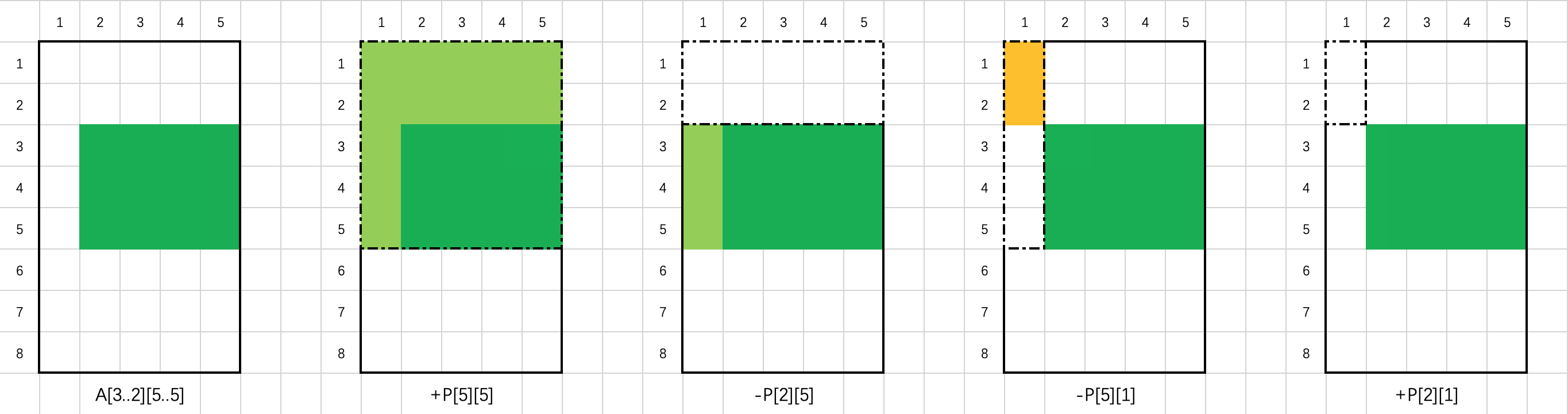
那么如何得到数组 P 呢？

我们按照行优先的顺序依次计算数组 P 中的每个元素，即当我们在计算 P[i][j] 时，数组 P 的前 i - 1 行，以及第 i 行的前 j - 1 个元素都已经计算完成。此时我们可以考虑 (i, j) 这个 1 * 1 的矩形区域，根据上面的等式，有：

A[i][j] = P[i][j] - P[i - 1][j] - P[i][j - 1] + P[i - 1][j - 1]

由于等式中的 A[i][j]，P[i - 1][j]，P[i][j - 1] 和 P[i - 1][j - 1] 均已知，我们可以通过：

P[i][j] = P[i - 1][j] + P[i][j - 1] - P[i - 1][j - 1] + A[i][j]

在O(1) 的时间计算出 P[i][j]。因此按照行优先的顺序，我们可以在 O(MN) 的时间得到数组 P。在此之后，我们就可以很方便地在 O(1) 的时间内求出任意一个矩形区域的元素之和了。

 

注意事项：

在大部分语言中，数组下标是从 0 而不是 1 开始，在实际的代码编写过程中需要考虑这一情况。

 

 

代码

需要注意的是为了计算方便，前缀和的下标比矩阵的下标大1

python3

class PrefixSum:
    def getPrefixSum(selfself, mat):
        m, n = len(mat), len(mat[0])

        # data 为二维前缀和数组
        data = [[0] * (n + 1) for _ in range(m + 1)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                data[i][j] = data[i - 1][j] + data[i][j - 1] - data[i - 1][j - 1] + mat[i - 1][j - 1]

        # 获取任意矩形的面积
        def getRect(x1, y1, x2, y2):
            return data[x2][y2] - data[x1 - 1][y2] - data[x2][y1 - 1] + data[x1 - 1][y1 - 1]

 

c++

class Solution {
public:
    int getRect(const vector<vector<int>>& P, int x1, int y1, int x2, int y2) {
        return P[x2][y2] - P[x1 - 1][y2] - P[x2][y1 - 1] + P[x1 - 1][y1 - 1];
    }

    int maxSideLength(vector<vector<int>>& mat, int threshold) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> P(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                P[i][j] = P[i - 1][j] + P[i][j - 1] - P[i - 1][j - 1] + mat[i - 1][j - 1];
            }
        }
}

 

例题：

矩阵区域和

给你一个 m x n 的矩阵 mat 和一个整数 k ，请你返回一个矩阵 answer ，其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和： 

i - k <= r <= i + k,
j - k <= c <= j + k 且
(r, c) 在矩阵内。

示例 1：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[12,21,16],[27,45,33],[24,39,28]]
示例 2：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出：[[45,45,45],[45,45,45],[45,45,45]]

提示：

m == mat.length
n == mat[i].length
1 <= m, n, k <= 100
1 <= mat[i][j] <= 100

题解：

思路很简单，就是prime【i】【j】代表从下标0,0到下标i+1，j+1的两点为对角线的矩阵的总和，那么题目要求的区域和，就是从i+1，j+1向四方扩展长度k。行边界即i-k-1，i+k，列边界即j-k-1，j+k。需要注意的是为了计算方便，前缀和的下标比矩阵的下标大1，

放一个JAVA版本解答：

class Solution {
    public int[][] matrixBlockSum(int[][] mat, int k) { 
        int n=mat.length,m=mat[0].length;
        int[][] dp=new int[n+1][m+1];
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                dp[i][j]=dp[i-1][j]+dp[i][j-1]+mat[i-1][j-1]-dp[i-1][j-1];
            }
        }
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                int x1=i-k,y1=j-k,x2=i+k,y2=j+k;
                if(x1<1) x1=1;
                if(y1<1) y1=1;
                if(x2>n) x2=n;
                if(y2>m) y2=m;
                mat[i-1][j-1]=dp[x2][y2]+dp[x1-1][y1-1]-dp[x1-1][y2]-dp[x2][y1-1];
            }
        }
        return mat;
    }
}