中缀表达式转后缀表达式
1、中缀表达式和后缀表达式
中缀表达式就是我们正常使用的那种,例如:a+b*c
后缀表达式就是abc*+;
为什么要有中缀表达式和后缀表达式呢?
因为中缀表达式便于人们的理解与计算,但是后缀表达式更方便计算机的运算(如二叉树、堆栈的方法计算),因此在读取一个中缀表达式后,将其转化为后缀表达式更有利于计算
2、中缀表达式转后缀表达式
首先假设我们需要转化的中缀表达式为:
a + b * c + ( d * e + f ) * g
其转换成后缀表达式则为 a b c * + d e * f + g * +
2.1 基于堆栈的方法
转换过程需要用到栈,具体过程如下:
1、从左到右扫描每一个字符,如果遇到操作数,我们就直接将其输出。
2、如果遇到操作符,有如下几种情况
1)如果堆栈是空的,直接将操作符存储到堆栈中 (push)
2)如果该操作符的优先级大于栈顶的操作符,就直接将操作符存储到堆栈中(push)
3)如果该操作符的优先级低于堆栈出口的操作符,就将堆栈出口的操作符导出(pop), 直到该操作符的优先级大于堆栈顶端的操作符。将扫描到的操作符导入到堆栈中(push)
-
- 优先级 "()" > "*/" > "+-"
- 只有在遇到" ) "的情况下我们才弹出" ( ",其他情况我们都不会弹出" ( "。这一点根据优先级也很好理解,括号的优先级最高
4)如果遇到一个右括号,则将栈元素弹出,将弹出的操作符输出直到遇到左括号为止。注意,左括号只弹出并不输出
3、如果我们读到了输入的末尾,则将栈中所有元素依次弹出。
图解过程如下:
1、从左到右扫描每一个字符,如果遇到操作数,我们就直接将其输出。
2、如果遇到操作符,有如下几种情况
1)如果堆栈是空的,直接将操作符存储到堆栈中 (push)

2)如果该操作符的优先级大于栈顶的操作符,就直接将操作符存储到堆栈中(push)
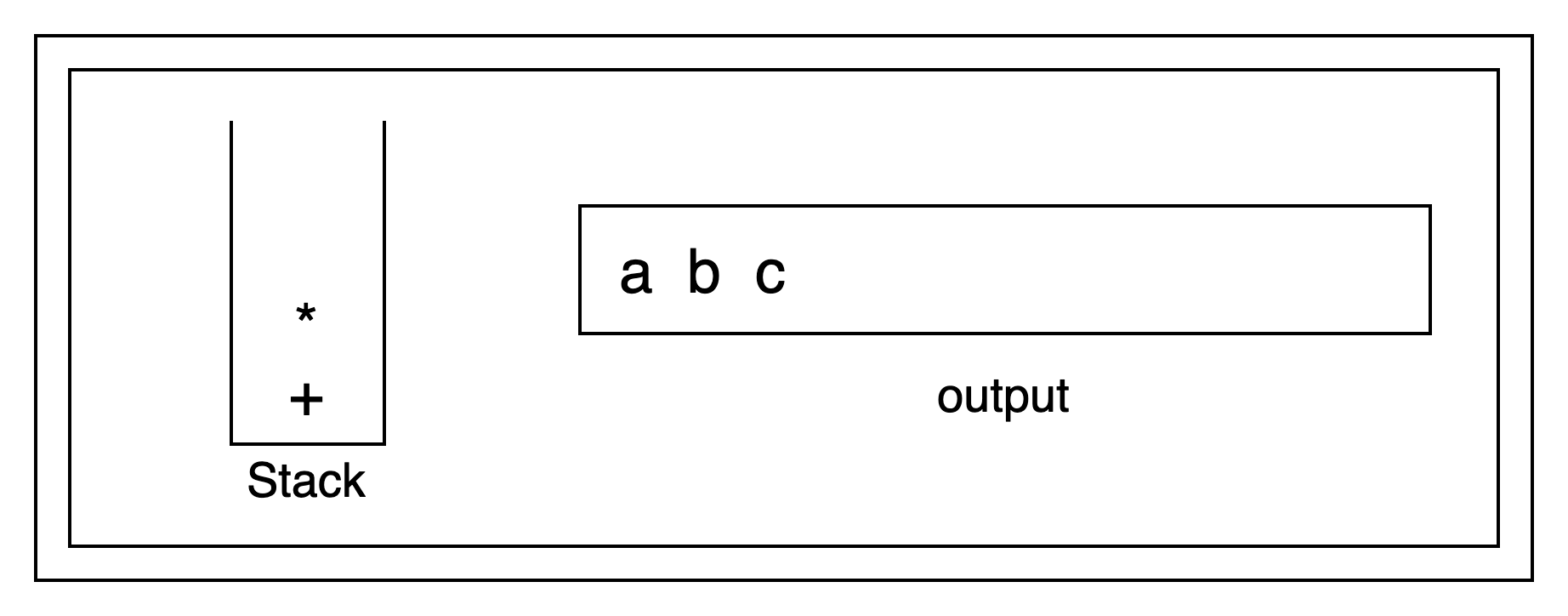
3)如果该操作符的优先级低于堆栈出口的操作符,就将堆栈出口的操作符导出(pop), 直到该操作符的优先级大于堆栈顶端的操作符。将扫描到的操作符导入到堆栈中(push)
遇到『+』号,当前栈中的元素为『*, +』,优先级都不低于当前操作符『+』,故先弹出,『+』再入栈
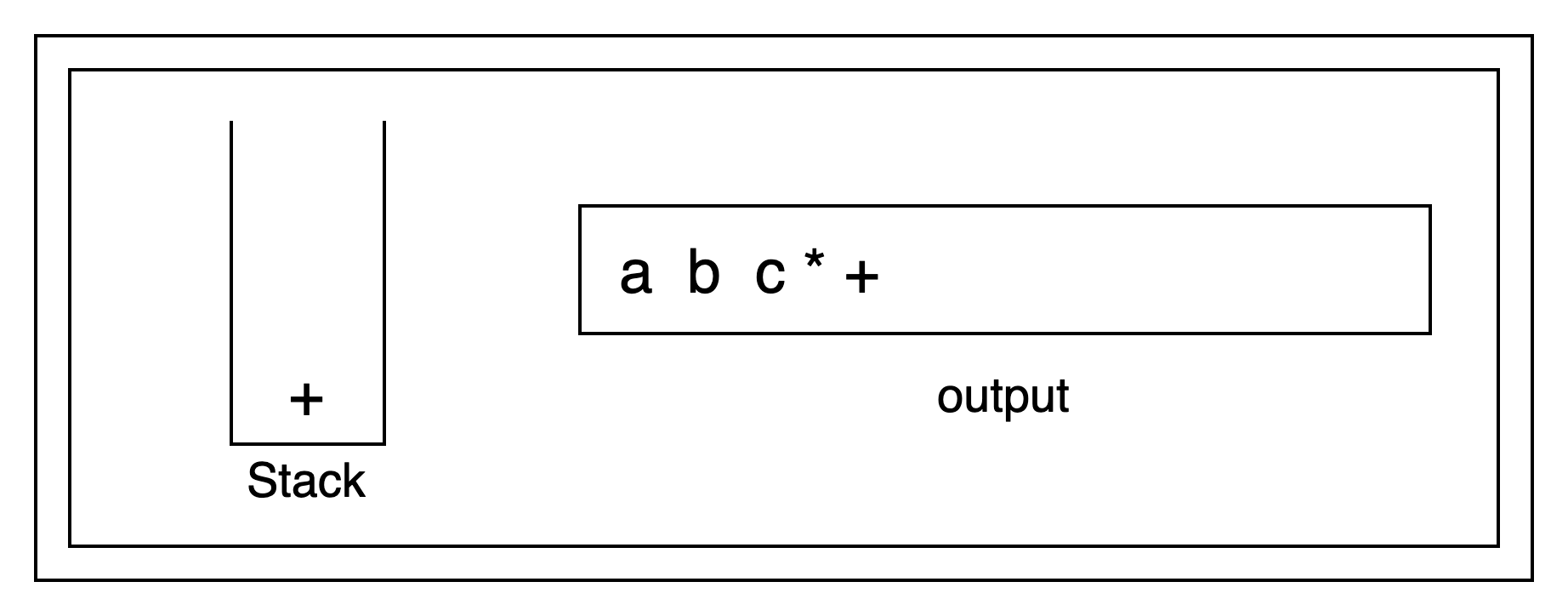
遇到『(』号,优先级最高,『(』直接入栈,操作数直接输出
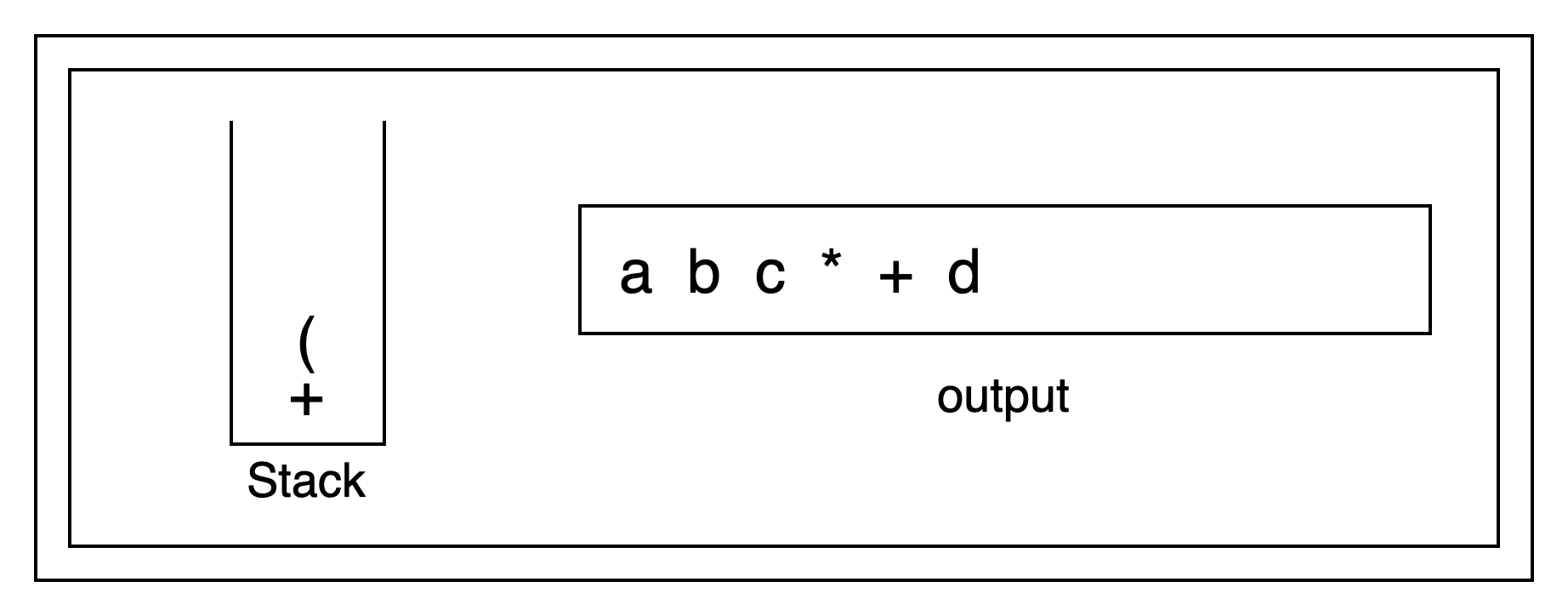
遇到『*』号,优先级高,『(』是栈顶元素,因此直接入栈,操作数直接输出

遇到『+』号,优先级低,『*』是栈顶元素,先出栈,『+』再入栈,操作数直接输出

4)如果遇到一个右括号,则将栈元素弹出,将弹出的操作符输出直到遇到左括号为止。注意,左括号只弹出并不输出

『*』入栈,操作数输出

3、如果我们读到了输入的末尾,则将栈中所有元素依次弹出。

代码
1 # 使用堆栈 2 def getPostExpByStack(inExp): 3 re = [] 4 op = [] 5 while inExp: 6 tem = inExp.pop(0) 7 if not isOperator(tem): 8 re.append(tem) 9 else: 10 if tem == '(': 11 op.append(tem) 12 elif tem == ')': 13 while op[-1] != "(": 14 re.append(op.pop()) 15 op.pop() 16 elif tem in ['+', '-', '*', '/']: 17 while op and op[-1] != "(" and getOperOrder(op[-1]) >= getOperOrder(tem): 18 re.append(op.pop()) 19 op.append(tem) 20 21 if op: 22 re = re + op[::-1] 23 24 return re
2.2 括号法
好记又简单,转换过程如下
1、根据运算符的优先级对中缀表达式加括号(有几个运算符就有几对括号)(原本有的括号不用加)
式子变成:( ( a + ( b * c) ) + ( ( ( d * e ) + f ) * g ) )
2、转换前缀与后缀表达式
1)前缀:把运算符号移动到对应的括号前面
则变成:+ ( + ( a * ( b c) ) * ( + ( * ( d e ) f ) g ) )
把括号去掉:+ + a * b c * + * d e f g 即为前缀表达式
2)后缀:把运算符号移动到对应的括号后面
则变成拉:((a(bc)*)+(((de)*f)+g)*)+
把括号去掉:abc*+de*f+g *+ 即为后缀表达式
代码:
待补充
2.3 生成二叉树以后遍历
重点是如何生成二叉树
代码

1 import re 2 3 4 # 定义二叉树节点 5 class TNode: 6 def __init__(self, x): 7 self.val = x 8 self.left = None 9 self.right = None 10 11 12 # 判断是否是运算符 13 def isOperator(ch): 14 if ch in ['+', '-', '*', '/', '^', '(', ')']: 15 return True 16 return False 17 18 19 # 判断优先级 20 def getOperOrder(self, ch): 21 if ch == '(': 22 return 1 23 if ch in ['+', '-']: 24 return 2 25 if ch in ['*', '/']: 26 return 3 27 if ch == '^': 28 return 4 29 return 0 30 31 32 # 二叉树操作类 33 class Solution: 34 35 # 后缀表达式生成二叉树 36 def postExpToTree(self, exp): 37 if not exp: 38 return 39 re = [] 40 while exp: 41 tem = exp.pop(0) 42 if not isOperator(tem): 43 re.append(TNode(tem)) 44 else: 45 p = TNode(tem) 46 p.right = re.pop() 47 p.left = re.pop() 48 re.append(p) 49 return re.pop() 50 51 # 前缀表达式生成二叉树 52 def PreExpTree(self, exp): 53 re = [] 54 while exp: 55 tmp = exp.pop() 56 if not isOperator(tmp): 57 re.append(TNode(tmp)) 58 else: 59 p = TNode(tmp) 60 p.left = re.pop() 61 p.right = re.pop() 62 re.append(p) 63 return re.pop() 64 65 # 中缀表达式生成二叉树 66 # 1、可以先将中缀表达式转换成后缀表达式,在用后缀表达式的方式生成二叉树 见方法 堆栈生成中缀表达式 67 # 2、直接生成二叉树 68 def InexpTree(self, exp): 69 pro = dict(zip('(+-*/', [0, 1, 1, 2, 2])) 70 stack, ops = [], [] 71 for left, num, op, right in re.findall(r'(\()|(\d+)|([-+*/])|(\))', s + '+'): 72 if left: 73 ops.append(left) 74 elif num: 75 stack.append(TNode(num)) 76 elif op: 77 while ops and pro[ops[-1]] >= pro[op]: 78 r, l = stack.pop(), stack.pop() 79 stack.append(TNode(ops.pop(), l, r)) 80 ops.append(op) 81 else: 82 while ops[-1] != '(': 83 r, l = stack.pop(), stack.pop() 84 stack.append(TNode(ops.pop(), l, r)) 85 ops.pop() 86 return stack[0]
3、中缀表达式和后缀表达式求值
3.1 后缀表达式求值
逆波兰表达式求值
1 class Solution: 2 def evalRPN(self, tokens: List[str]) -> int: 3 data_stack = [] 4 for i in tokens: 5 if i not in ['+', '-', '*', '/']: 6 data_stack.append(int(i)) 7 else: 8 b = data_stack.pop() 9 a = data_stack.pop() 10 if i == '+': 11 res = a + b 12 elif i == '-': 13 res = a - b 14 elif i == '*': 15 res = a * b 16 else: 17 res = int(a / b) 18 data_stack.append(res) 19 20 return data_stack[-1]
3.2 中缀表达式求值
基本计算器
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
示例 1:
输入:s = "1 + 1"
输出:2
示例 2:输入:s = " 2-1 + 2 "
输出:3
示例 3:输入:s = "(1+(4+5+2)-3)+(6+8)"
输出:23
方法一:括号展开 + 栈
由于字符串除了数字与括号外,只有加号和减号两种运算符。因此,如果展开表达式中所有的括号,则得到的新表达式中,数字本身不会发生变化,只是每个数字前面的符号会发生变化。
因此,我们考虑使用一个取值为 {−1,+1} 的整数 sign 代表「当前」的符号。根据括号表达式的性质,它的取值:
与字符串中当前位置的运算符有关;
如果当前位置处于一系列括号之内,则也与这些括号前面的运算符有关:每当遇到一个以 − 号开头的括号,则意味着此后的符号都要被「翻转」。
考虑到第二点,我们需要维护一个栈 ops,其中栈顶元素记录了当前位置所处的每个括号所「共同形成」的符号。例如,对于字符串 1+2+(3-(4+5)):
扫描到 1+2 时,由于当前位置没有被任何括号所包含,则栈顶元素为初始值 +1;
扫描到 1+2+(3 时,当前位置被一个括号所包含,该括号前面的符号为 + 号,因此栈顶元素依然 +1;
扫描到 1+2+(3-(4 时,当前位置被两个括号所包含,分别对应着 + 号和 − 号,由于 + 号和 − 号合并的结果为 − 号,因此栈顶元素变为 −1。
在得到栈 ops 之后, sign 的取值就能够确定了:如果当前遇到了 + 号,则更新 sign←ops.top();如果遇到了遇到了 − 号,则更新 sign←−ops.top()。
然后,每当遇到 ( 时,都要将当前的 sign 取值压入栈中;每当遇到 ) 时,都从栈中弹出一个元素。这样,我们能够在扫描字符串的时候,即时地更新 ops 中的元素。
1 class Solution: 2 def calculate(self, s: str) -> int: 3 ops = [1] 4 sign = 1 5 6 ret = 0 7 n = len(s) 8 i = 0 9 while i < n: 10 if s[i] == ' ': 11 i += 1 12 elif s[i] == '+': 13 sign = ops[-1] 14 i += 1 15 elif s[i] == '-': 16 sign = -ops[-1] 17 i += 1 18 elif s[i] == '(': 19 ops.append(sign) 20 i += 1 21 elif s[i] == ')': 22 ops.pop() 23 i += 1 24 else: 25 num = 0 26 while i < n and s[i].isdigit(): 27 num = num * 10 + ord(s[i]) - ord('0') 28 i += 1 29 ret += num * sign 30 return ret
方法二:转逆波兰表达式
见上
方法三:eval()
过不了全部测试样例




