不同语言中的除法

前言

今天看到一道题目：逆波兰表达式求值，如下：

根据 逆波兰表示法，求表达式的值。

有效的算符包括 +、-、*、/ 。每个运算对象可以是整数，也可以是另一个逆波兰表达式。

 

说明：

整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说，表达式总会得出有效数值且不存在除数为 0 的情况。
 

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9
示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6
示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：
该算式转化为常见的中缀算术表达式为：
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

解答

其实这道题本事并不难，用栈即可。

逆波兰表达式严格遵循「从左到右」的运算。计算逆波兰表达式的值时，使用一个栈存储操作数，从左到右遍历逆波兰表达式，进行如下操作：

如果遇到操作数，则将操作数入栈；
如果遇到运算符，则将两个操作数出栈，其中先出栈的是右操作数，后出栈的是左操作数，使用运算符对两个操作数进行运算，将运算得到的新操作数入栈。
整个逆波兰表达式遍历完毕之后，栈内只有一个元素，该元素即为逆波兰表达式的值。

 

面对这种简单题，我重拳出击，写下了如下代码：

class Solution(object):
    def evalRPN(self, tokens):
        """
        :type tokens: List[str]
        :rtype: int
        """
        data_stack = []
        for i in tokens:
            if i not in ['+', '-', '*', '/']:
                data_stack.append(int(i))
            else:
                b = data_stack.pop()
                a = data_stack.pop()
                if i == '+':
                    res = a + b
                elif i == '-':
                    res = a - b
                elif i == '*':
                    res = a * b
                else:
                    res = a // b
                data_stack.append(res)
        return data_stack[-1]

测了前两个用例，通过，完美，提交，哦豁，错了，错误用例正好就是第三个测试用例。

我以为有哪里不对，于是我打印了每一步的计算过程，终于发现了问题

在计算 6 / -132 的时候，题解中给的解答是：

6 / -132  = 0 

但是，我的解答是

6 // -132 = -1 （python 的"/" 是真正的除法， 一般用『/』取整）

因此，也就引入了今天的问题。

 

python3

• 真除法： /

 

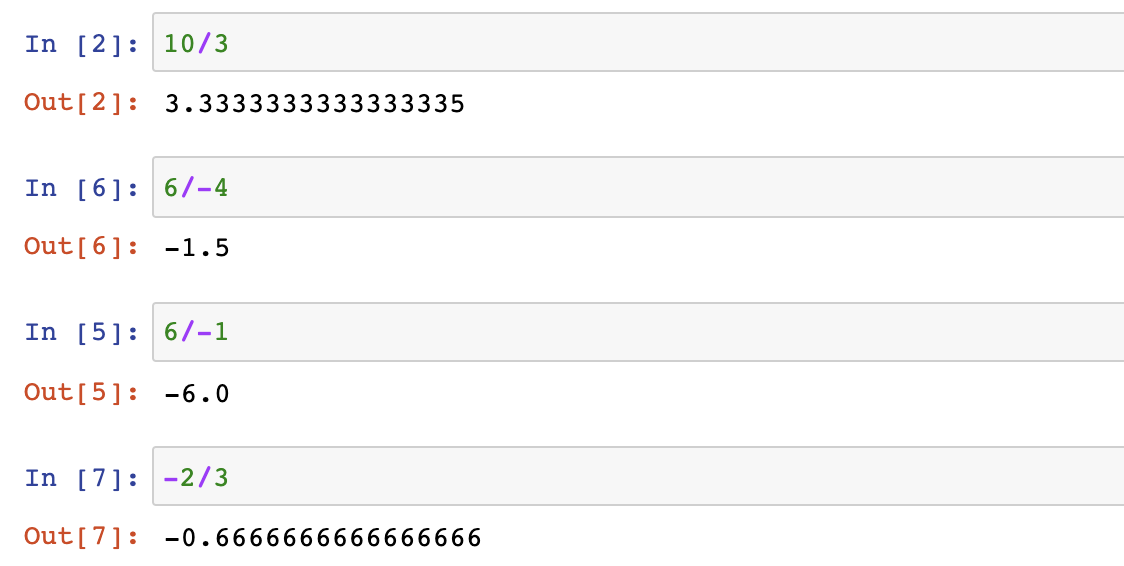
• 地板除 实质是向下取整 // 

  

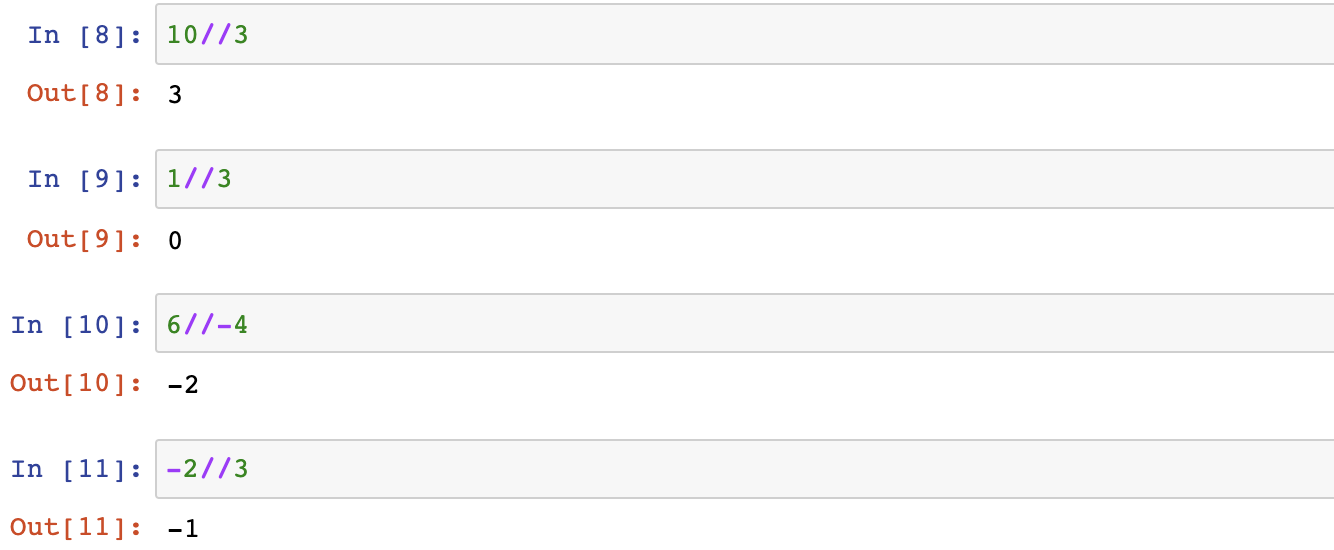
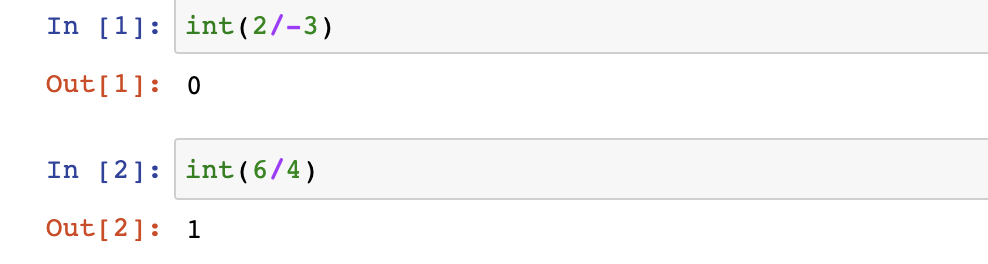
• int() 直接截断 小数取整会采用比较暴力的截断方式 正数和负数是不一样的，注意和//的区别

 

• math.ceil() 向上取整

math.floor() 向下取整 

 

 

 

Java

public class TestDivide {
    public static void main(String[] args) {
        System.out.println("截取整数部分");
        System.out.println("1 / 3 = " + 1 / 3);
        System.out.println("6 / 3 = " + 6 / 3);
        System.out.println("6 / 4 = " + 6 / 4);
        System.out.println("-3 / 2 = " + -3 / 2);
        
        System.out.println("真实除法");
        System.out.println("1.0 / 3 = " + 1.0 / 3);
        System.out.println("6.0 / 3 = " + 6.0 / 3);
        System.out.println("6.0 / 4  = " + 6.0 / 4);
        System.out.println("-3.0 / 2 = " + -3.0 / 2);

        System.out.println("向上取整");
        System.out.println("Math.ceil(-1.1) = " + Math.ceil(-1.1));
        System.out.println("Math.ceil(-1.5) = " + Math.ceil(-1.5));
        System.out.println("Math.ceil(1.1) = " + Math.ceil(1.1));
        System.out.println("Math.ceil(1.5) = " + Math.ceil(1.5));

        System.out.println("向下取整");
        System.out.println("Math.floor(-1.1) = " + Math.floor(-1.1));
        System.out.println("Math.floor(-1.5) = " + Math.floor(-1.5));
        System.out.println("Math.floor(1.1) = " + Math.floor(1.1));
        System.out.println("Math.floor(1.5) = " + Math.floor(1.5));
    }
}

结果如下：

>>>
   截取整数部分
1 / 3 = 0
6 / 3 = 2
6 / 4 = 1
-3 / 2 = -1
真实除法
1.0 / 3 = 0.3333333333333333
6.0 / 3 = 2.0
6.0 / 4  = 1.5
-3.0 / 2 = -1.5
向上取整
Math.ceil(-1.1) = -1.0
Math.ceil(-1.5) = -1.0
Math.ceil(1.1) = 2.0
Math.ceil(1.5) = 2.0
向下取整
Math.floor(-1.1) = -2.0
Math.floor(-1.5) = -2.0
Math.floor(1.1) = 1.0
Math.floor(1.5) = 1.0

 

 

Go

import (
    "fmt"
    "math"
)

func main() {
    x := 1.1
    fmt.Println(1 / 2)  // 0
    fmt.Println(1 / 3)  // 0
    fmt.Println(-1 / 3) // 0
    fmt.Println(-4 / 5) // 0

    fmt.Println(1.0 / 2)  // 0.5
    fmt.Println(1.0 / 3)  // 0.33333333333
    fmt.Println(-1.0 / 3) // -0.333333333333
    fmt.Println(-4.0 / 5) // -0.8

    fmt.Println(math.Ceil(x))  // 2
    fmt.Println(math.Floor(x)) // 1
}