快速幂

引入：

先来看一道题：怎么计算pow(x,n)?

最直观的，暴力解法

class Solution {
    public double myPow(double x, int n) {
        long N = n;
        if (N < 0) {
            x = 1 / x;
            N = -N;
        }
        double ans = 1;
        for (long i = 0; i < N; i++)
            ans = ans * x;
        return ans;
    }
}

不过，暴力魔法不可取，虽然有时候直观且有效。。

考虑 x的11次方：

x¹¹  = x⁵ * x⁵ * x

x⁵ = x² * x² * x

x² = x * x

模仿这样的过程，我们得到一个在  时间内计算出幂的算法，也就是快速幂。

 

递归快速幂：

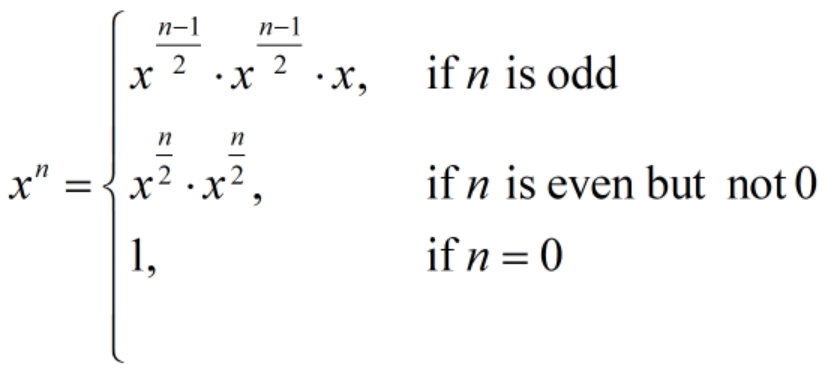
• 计算a的n次方，如果n是偶数（不为0），那么就先计算a的n/2次方，然后平方；
• 如果n是奇数，那么就先计算a的n-1次方，再乘上a
• 递归的边界为 n = 0，任意数的 0 次方均为 1。

于是，算法可以写成：

class Solution {
    public double myPow(double x, int n) {
        long N = n;
        return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
    }

    public double quickMul(double x, long N) {
        if (N == 0) {
            return 1.0;
        }
        double y = quickMul(x, N / 2);
        return N % 2 == 0 ? y * y : y * y * x;
    }
}

 

迭代快速幂：

由于递归需要使用额外的栈空间，我们试着将递归转写为迭代。

根据快速幂的原理， 将11拆成1+2+8，也就是2⁰ + 2¹ + 2³，在观察11的二进制1011(从右到左观察)，说白了就是二进制和十进制间的转换，二进制到十进制，0不起作用

也就是，有如下等式：

这样一来，我们从 x 开始不断地进行平方，得到 x², x⁴, x⁸, x¹⁶，如果 n 的第 k 个（从右往左，从 0 开始计数）二进制位为 1，那么我们就将对应的贡献 x^{2^k}计入答案。

class Solution {
    public double myPow(double x, int n) {
        long N = n;
        return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
    }

    public double quickMul(double x, long N) {
        double ans = 1.0;
        // 贡献的初始值为 x
        double x_contribute = x;
        // 在对 N 进行二进制拆分的同时计算答案
        while (N > 0) {
            if (N % 2 == 1) {
                // 如果 N 二进制表示的最低位为 1，那么需要计入贡献
                ans *= x_contribute;
            }
            // 将贡献不断地平方
            x_contribute *= x_contribute;
            // 舍弃 N 二进制表示的最低位，这样我们每次只要判断最低位即可
            N /= 2;
        }
        return ans;
    }
}

 

矩阵快速幂

矩阵快速幂，就是利用矩阵相乘，把上边的数字x换成矩阵A，然后再写一个函数，去计算两个矩阵的乘积

对于数字，初始化为1， 对于矩阵呢，初始化当然是E了，也就是单位矩阵，因为A*E=A

class Solution {
    static final int MOD = 1000000007;

    public int fib(int n) {
        if (n < 2) {
            return n;
        }
        int[][] q = {{1, 1}, {1, 0}};
        int[][] res = pow(q, n - 1);
        return res[0][0];
    }

    public int[][] pow(int[][] a, int n) {
        int[][] ret = {{1, 0}, {0, 1}};
        while (n > 0) {
            if ((n & 1) == 1) {
                ret = multiply(ret, a);
            }
            n >>= 1;
            a = multiply(a, a);
        }
        return ret;
    }

    public int[][] multiply(int[][] a, int[][] b) {
        int[][] c = new int[2][2];
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                c[i][j] = (int) (((long) a[i][0] * b[0][j] + (long) a[i][1] * b[1][j]) % MOD);
            }
        }
        return c;
    }
}