字符串匹配之Sunday 算法

Sunday 算法

　　Sunday 算法是 Daniel M.Sunday 于1990年提出的字符串模式匹配。其核心思想是：在匹配过程中，模式串发现不匹配时，算法能跳过尽可能多的字符以进行下一步的匹配，从而提高了匹配效率。

匹配过程

　　从前往后匹配，在匹配失败时关注的是主串中参加匹配的最末位字符的下一位字符。

• • 如果该字符没有在模式串中出现则直接跳过，即移动位数 = 模式串长度 + 1；
  • 否则，其移动位数 = 模式串长度 - 该字符最右出现的位置(以0开始) = 模式串中该字符最右出现的位置到尾部的距离 + 1。

案例（转载自（小浩学算法—字符串系列：实现sunday匹配））

　　

一般来讲，字符串匹配算法第一步，都是把目标串和模式串对齐。不管是KMP，BM，SUNDAY都是这样。

而对于SUNDAY算法，我们从头部开始比较，一旦发现不匹配，直接找到主串中位于模式串后面的第一个字符，即下面绿色的 “s”。（这里说明一下，为什么是找模式串后面的第一个字符。在把模式串和目标串对齐后，如果发现不匹配，那肯定需要移动模式串。问题是需要移动多少步。各字符串匹配算法之间的差别也来自于这个地方，对于KMP，是建立部分匹配表来计算。BM，是反向比较计算移动量。对于SUNDAY，就是找到模式串后的第一个字符。因为，无论模式串移动多少步，模式串后的第一个字符都要参与下一次比较，也就是这里的 “s”）

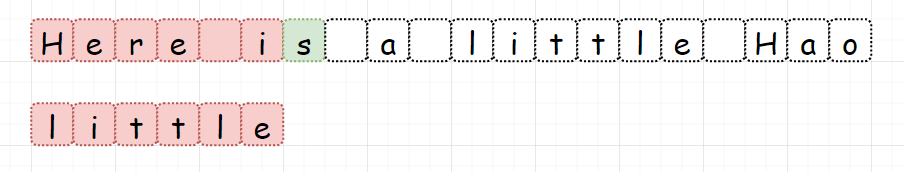
找到了模式串后的第一个字符 “s”，接下来该怎么做？我们需要查看模式串中是否包含这个元素，如果不包含那就可以跳过一大片，从该字符的下一个字符开始比较。

因为仍然不匹配（空格和l），我们继续重复上面的过程。找到模式串的下一个元素：t

现在有意思了，我们发现 t 被包含于模式串中，并且 t 出现在模式串倒数第3个。所以我们把模式串向前移动3个单位：

 

有内味了，我们发现竟然匹配成功了，是不是很神奇？证明的过程今天暂且不谈（后面我会出一个算法证明篇，来证明之前讲过的一些算法。我需要你做的是，掌握上面这些！）

 

捞干货，这个过程里我们做了一些什么：

• 对齐目标串和模式串，从前向后匹配
• 关注主串中位于模式串后面的第一个元素（核心）
• 如果关注的字符没有在子串中出现则直接跳过
• 否则开始移动模式串，移动位数 = 子串长度 - 该字符最右出现的位置(以0开始)

 

应用

实现 strStr()

　　给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回  -1。

示例 1:

输入: haystack = "hello", needle = "ll"
输出: 2

示例 2:

输入: haystack = "aaaaa", needle = "bba"
输出: -1

class Solution {
public:
    int strStr(string haystack, string needle) {
        int len_h = haystack.length();
        int len_n = needle.length();
        if (len_h==0)
            if(len_n==0)
                return 0;
            else
                return -1;

        if (len_h<len_n)
            return -1;
        
        int hIndex = 0;
        int nIndex = 0;
        while(nIndex < len_n)
        {
            if(hIndex > len_h-1)
                return -1;
            if(haystack[hIndex] == needle[nIndex])
            {
                hIndex++;
                nIndex++;
            }
            else
            {
                int nextIndex = hIndex-nIndex+len_n;
                if(nextIndex<len_h)
                {
                    int step = needle.rfind(haystack[nextIndex]);
                    if(step==-1)
                    {
                        hIndex = nextIndex+1;
                    }
                    else
                    {
                        hIndex = nextIndex-step;
                    }
                    nIndex = 0;
                }
                else
                    return -1;
            }
        }
        return hIndex-nIndex;
    }
};