单调栈

1、分类

• 单调递增栈：数据出栈的序列为单调递增序列
• 单调第减栈：数据出栈的序列为单调递减序列

 

2、操作（以单调递增栈为例）

• 如果新元素比栈顶元素大， 入栈
• 如果新元素比栈顶元素小，栈顶元素出栈，直到栈顶元素小于该元素，入栈该元素

 

3、示例

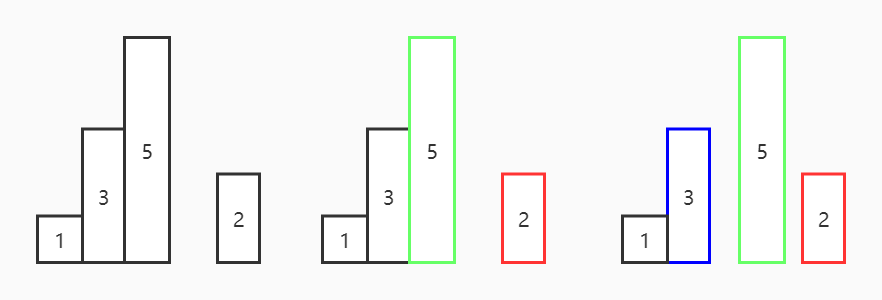
例如，给定一个序列 [ 1, 3, 5, 2, 4 ]，当1，3，5入栈以后，当遇到新元素2时，由于栈顶元素5 > 2， 5被弹出， 新元素2是出栈元素5右边第一个比 5 小的元素，即新元素是出栈元素向后找第一个比其小的元素；此时新栈顶元素为3，3是5左边第一个比5小的数字，即新栈顶元素是出栈元素向前找第一个比其小的元素。

 

 

 

4、代码块

stack = []
for i in range(len(nums)):
    while stack and stack.top() > nums[i]:
        stack.pop()
    stack.push(nums[i])

 

5、应用

a.柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

 

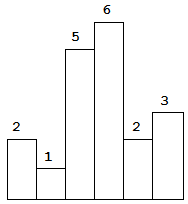
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

 

 

 

 

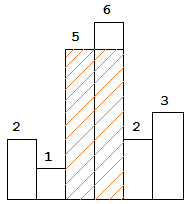
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

 

思路

1. 1. 对于一个高度，如果能得到向左和向右的边界
   2. 那么就能对每个高度求一次面积
   3. 遍历所有高度，即可得出最大面积
   4. 使用单调栈，在出栈操作时得到前后边界并计算面积

代码：

'''
1、为了方便计算，栈里面存储的位置
2、数组末尾加入了一个height 0，来强迫程序在结束前，将所有元素按照顺序弹出栈。
'''

class Solution:
    def largestRectangleArea(self, heights):
        heights.append(0)
        stack = []
        res = 0

        for i in range(len(heights)):
            while stack and heights[stack[-1]] > heights[i]:
                s = stack.pop()
                res = max(res, heights[s] * ((i - stack[-1] - 1) if stack else i))
            stack.append(i)
        return res

 

b. 最大矩形

（ps：话说这道题是我当年研究生联系导师的时候，老师给我出的题目，不过一直没做出来，手动笑哭）

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例:

输入:

[

["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]

]

输出: 6

思路：

　　这一题的算法本质上和上一题一样，对每一行都求出每个元素对应的高度，这个高度就是对应的连续1的长度，然后对每一行都更新一次最大矩形面积。那么这个问题就变成了柱状图中的最大矩形面积。本质上是对矩阵中的每行，均依次执行上一题的算法。

代码：

class Solution:
    def maximalRectangle(self, matrix: List[List[str]]) -> int:
        if len(matrix) == 0:
            return 0
        
        res = 0
        m, n = len(matrix),len(matrix[0])
        heights = [0] * n

        for i in range(m):
            for j in range(n):
                if matrix[i][j] == '0':
                    heights[j] = 0
                else:
                    heights[j] = heights[j] + 1
            
            res = max(res, self.largestRectangleArea(heights))
        
        return res


    
    def largestRectangleArea(self, heights):
        heights.append(0)
        stack = []
        res = 0

        for i in range(len(heights)):
            while stack and heights[stack[-1]] > heights[i]:
                s = stack.pop()
                res = max(res, heights[s] * ((i - stack[-1] - 1) if stack else i))
            stack.append(i)
        return res