快速排序及应用（快排查找第k大的数）

1、快排

　　基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

2、过程（引至快速排序）

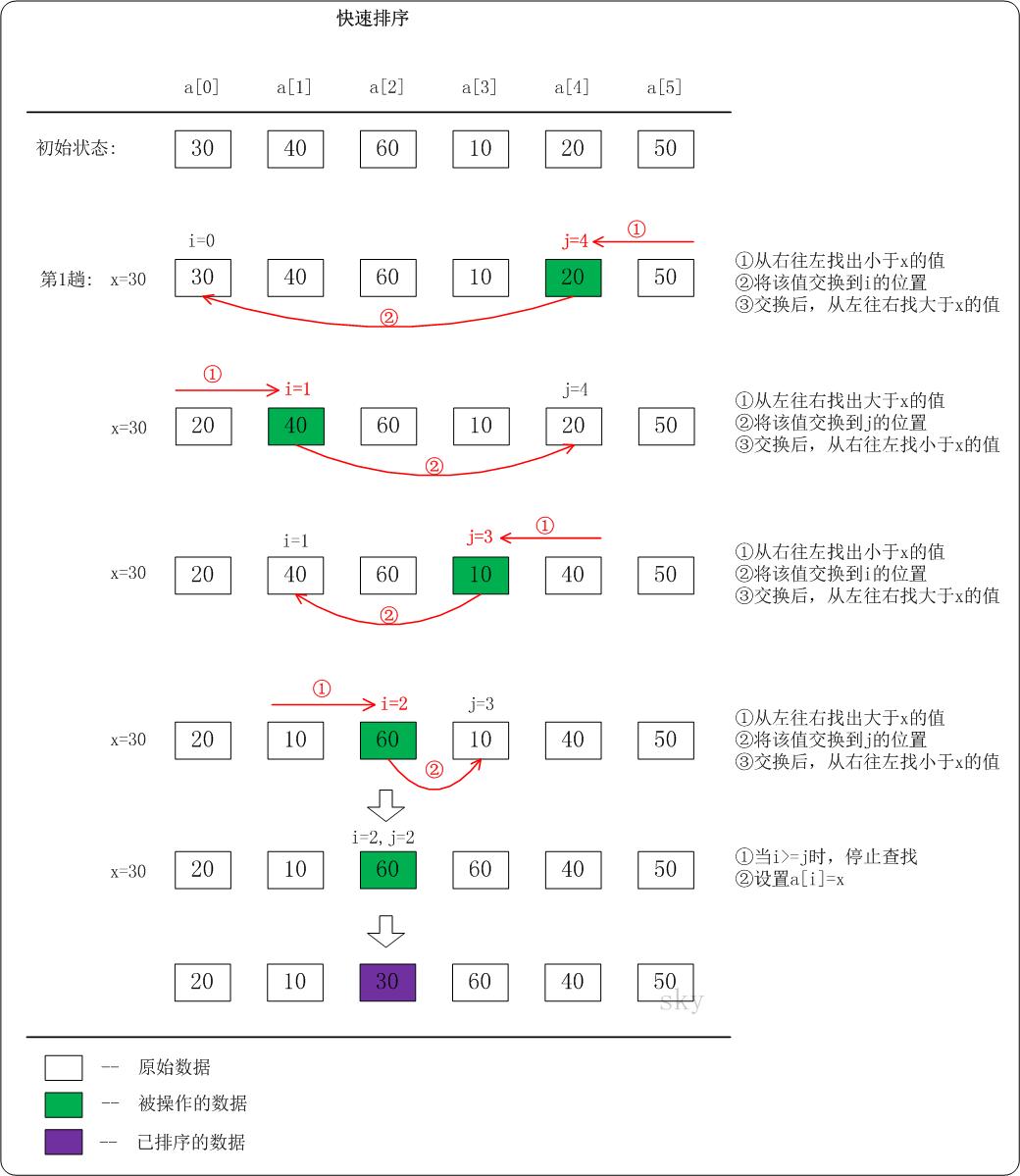
给出第1趟快速排序的流程。在第1趟中，设置x=a[i]，即x=30。
(01) 从"右 --> 左"查找小于x的数：找到满足条件的数a[j]=20，此时j=4；然后将a[j]赋值a[i]，此时i=0；接着从左往右遍历。
(02) 从"左 --> 右"查找大于x的数：找到满足条件的数a[i]=40，此时i=1；然后将a[i]赋值a[j]，此时j=4；接着从右往左遍历。
(03) 从"右 --> 左"查找小于x的数：找到满足条件的数a[j]=10，此时j=3；然后将a[j]赋值a[i]，此时i=1；接着从左往右遍历。
(04) 从"左 --> 右"查找大于x的数：找到满足条件的数a[i]=60，此时i=2；然后将a[i]赋值a[j]，此时j=3；接着从右往左遍历。
(05) 从"右 --> 左"查找小于x的数：没有找到满足条件的数。当i>=j时，停止查找；然后将x赋值给a[i]。此趟遍历结束！

按照同样的方法，对子数列进行递归遍历。最后得到有序数组！

　

 

 

3、复杂度和稳定性

• 快速排序是不稳定的
• 快速排序的平均时间复杂度是：O(nlogn)

4、代码

def parttion(v, left, right):
    key = v[left]
    low = left
    high = right
    while low < high:
        while (low < high) and (v[high] >= key):
            high -= 1
        v[low] = v[high]
        while (low < high) and (v[low] <= key):
            low += 1
        v[high] = v[low]
        v[low] = key
    return low
def quicksort(v, left, right):
    if left < right:
        p = parttion(v, left, right)
        quicksort(v, left, p-1)
        quicksort(v, p+1, right)
    return v


if __name__ == '__main__':
    s = [6, 8, 1, 4, 3, 9, 5, 4, 11, 2, 2, 15, 6]
    res = quicksort(s,0,len(s)-1)
    print(res)

5、应用

• 找到数组中第k大的数

# -*- coding:utf-8 -*-

def partition(nums, left, right):
    temp = nums[left]
    while left < right:
        while left < right and temp >= nums[right]:
            right -= 1
        nums[left] = nums[right]
        while left < right and temp < nums[left]:
            left += 1
        nums[right] = nums[left]
    nums[left] = temp
    return left


def quickSort_k(nums, left, right, k):
    if left <= right:
        pos = partition(nums, left, right)
        if pos == k - 1:
            return nums[pos]
        elif pos > k - 1:
            return quickSort_k(nums, left, pos - 1, k)
        elif pos < k - 1:
            return quickSort_k(nums, pos + 1, right, k)
    else:
        return -1

if __name__ == '__main__':
    s = [6, 8, 1, 4, 3, 9, 5, 4, 11, 2, 2, 15, 6]
    # 第k大，第1大是15
    print(quickSort_k(s, 0, len(s) - 1, 2))