KMP:字符串匹配算法的理解及python实现
1、背景
给定一个字符串text,和一个模式串pattern。让你判断text是否包含pattern,如果包含,则返回text中出现pattern的第一个字符的坐标。否则返回-1。如果pattern是空字符串(长度为0),则返回1
例如,给定两个字符串:
S="BBC ABCDAB ABCDABCDABDE"
P="ABCDABD"
返回:15
2、直观想法,暴力匹配。
2.1 规则
假设现在文本串S匹配到 i 位置,模式串P匹配到 j 位置,则有:
-
- 如果当前字符匹配成功(即S[i] == P[j]),则i+1,j+1,继续匹配下一个字符;
- 如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0。相当于每次匹配失败时,i 回溯, j 被置为0。
2.2 过程(以下过程摘自摘自阮一峰的字符串匹配的 KMP 算法,并作稍微修改)
1. 首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位(i=1,j=0)。

2. 因为B与A不匹配,搜索词再往后移。

3. 就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。(i=4,j=0)

4. 接着比较字符串和搜索词的下一个字符,还是相同。

5. 直到字符串有一个字符,与搜索词对应的字符不相同为止。(i=10,j=6)

6. 因为不匹配,重新执行第②条指令:“如果失配(即S[i]! = P[j]),令i = i - (j - 1),j = 0”。此时,i=5,j=0,相当于判断S[5]跟P[0]是否匹配。

至此,我们可以看到,如果按照暴力匹配算法的思路,尽管之前文本串和模式串已经分别匹配到了S[9]、P[5],但因为S[10]跟P[6]不匹配,所以文本串就得回溯到S[5],模式串回溯到P[0],从而让文本串又接着开始从S[5]跟模式串的P[0]去匹配。接下来的匹配过程无非就是类似的逻辑思路,直到找到匹配的字符串或文本串遍历结束退出。
2.3 代码

""" * 暴力匹配字符串算法 * 思路: * ①如果当前字符匹配成功(即S[i] == P[j]),则i+1,j+1 * ②如果失配(即S[i] != P[j]),令i = i - (j - 1),j = 0 .相当于每次匹配失败时,i 回溯,j 被置为0。 * 时间复杂度为O(mn)(m、n分别为文本串和模式串的长度)。无需扩展存储空间。 * @param text 文本串 * @param pattern 模式串 * @return pattern返回在text中的位置 """ def bruteForceSearchPatternInText(text, pattern): textLen = len(text) pLen = len(pattern) if textLen < pLen: return -1 i = 0 j = 0 while i < textLen and j < pLen: if text[i] == pattern[j]: # 如果当前字符匹配成功(即S[i] == P[j]),则i += 1,j += 1 i += 1 j += 1 else: i = i - (j - 1) j = 0 # 匹配成功,返回模式串p在文本串s中的位置,否则返回 - 1 if j == pLen: return i - j return -1 if __name__ == '__main__': text = "BBC ABCDAB ABCDABCDABDE" pattern = "ABCDABD" index = bruteForceSearchPatternInText(text, pattern) print(index)
3、KMP
3.1 KMP提出的原因
上面的算法分析过程中,第6步后,我们会发现S[5]肯定跟P[0]失配。为什么呢?因为在之前第4步匹配中,我们已经得知S[5] = P[1] = B,而P[0] = A,即P[1] != P[0],故S[5]必定不等于P[0],所以回溯过去必然会导致失配。那有没有一种算法,让i不往回退,只需要移动j 即可呢?答案是肯定的。这种算法就是KMP算法,它利用之前已经部分匹配这个有效信息,保持i 不回溯,通过修改j 的位置,让模式串尽量地移动到有效的位置。
3.2 基础概念:前缀和后缀
- 前缀:指的是字符串的子串中从原串最前面开始的子串,如abcdef的前缀有:a,ab,abc,abcd,abcde
- 后缀:指的是字符串的子串中在原串结尾处结尾的子串,如abcdef的后缀有:f,ef,def,cdef,bcdef
KMP算法引入了一个next数组,F[i]表示的是前i的字符组成的这个子串最长的相同前缀后缀的长度!
例如字符串aababaaba的相同前缀后缀有a和aaba,那么其中最长的就是aaba。
3.3 KMP算法的难理解之处与本文叙述的约定
虽然说网上关于KMP算法的博客、教程很多,但很多文章在定义方面又有细微的不同,比如说有些从1开始标号,有些next表示的是前一个而有些是当前的。因此,在这里先对下文做一些说明和约定。
- 本文中,所有的字符串从0开始编号
- 本文中,next数组,next[i]表示0~i-1的字符串的最长相同前缀后缀的长度。
3.4 next数组的应用
7. 一个基本事实是,在上述过程的第5步之后,当空格与 D 不匹配时,你其实是已经知道前面六个字符是 "ABCDAB"。KMP 算法的想法是,设法利用这个已知信息,不要把 "搜索位置" 移回已经比较过的位置,而是继续把它向后移,这样就提高了效率。
8. 怎么做到这一点呢?可以针对模式串,设置一个跳转数组next,这个数组是怎么计算出来的,后面再介绍,这里只要会用就可以了。
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 模式串 | A | B | C | D | A | B | D |
| next[i] | -1 | 0 | 0 | 0 | 0 | 1 | 2 |
9. 已知空格与 D 不匹配时,前面六个字符 "ABCDAB" 是匹配的。根据跳转数组可知,不匹配处 D 的 next 值为 2,因此接下来从模式串下标为 2 的位置开始匹配。因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动4位。

10. 因为空格与C不匹配,C 处的 next 值为 0,因此接下来模式串从下标为 0 处开始匹配。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。

11. 因为空格与 A 不匹配,此处 next 值为 - 1,表示模式串的第一个字符就不匹配,那么直接往后移一位。

12. 逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。

13. 逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。

理解:"部分匹配"的实质是,有时候,字符串头部和尾部会有重复。(参考:详解KMP算法)
为什么根据最长相同真前后缀的长度就可以实现在不匹配情况下的跳转呢?举个代表性的例子:假如i = 6时不匹配,此时我们是知道其位置前的字符串为ABCDAB,仔细观察这个字符串,首尾都有一个AB,既然在i = 6处的 D 不匹配,我们为何不直接把i = 2处的 C 拿过来继续比较呢,因为都有一个AB啊,而这个AB就是ABCDAB的最长相同真前后缀,其长度 2 正好是跳转的下标位置。
至此我们可以大概看出一点端倪,当匹配失败时,j要移动的下一个位置k,存在着这样的性质:最前面的k个字符和j之前的最后k个字符是一样的。如果用数学公式来表示是这样的:
P[0 ~ k-1] == P[j-k ~ j-1]
这个相当重要,如果觉得不好记的话,可以通过下图来理解:
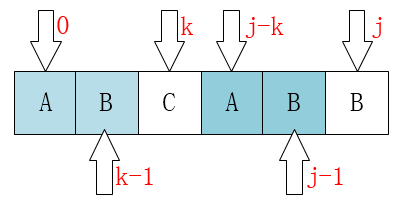
弄明白了这个就应该可能明白为什么可以直接将j移动到k位置了。
因为:(T是字符串,P是pattern,下同)
当T[i] != P[j]时
有T[i-j ~ i-1] == P[0 ~ j-1]
由P[0 ~ k-1] == P[j-k ~ j-1]
必然:T[i-k ~ i-1] == P[0 ~ k-1]
公式很无聊,能看明白就行了,不需要记住。
这一段只是为了证明我们为什么可以直接将j移动到k而无须再比较前面的k个字符。
3.5 next数组的性质和实现
- next[0] = -1,next [1] = 0恒成立。代表的意思是如果T[i]!=P[0]的话,那i就应该切换到下一个了。next[i] : 表示i前面元素的字符串的前缀和后缀公共元素的最大长度.
- 如果P[j] == P[k]的话,那么next[j+1] = k + 1。根据我们的定义next[j] = k => P[0~k-1] == P[j-k~j-1]。那么此时P[j] == P[k] => P[0~k] == P[j-k~j] => next[j+1] = k+1。
- 如果P[j] != P[k],那么k=next[k]。如何理解呢?同样以下图为例,这时候我们要判断的是next[j+1]的值,但是我们知道p[k] != p[j],所以我们肯定不能移动到k的位置,必须移动到k之前的某个位置,k=next[k],再进行迭代,直到找到p[j] == p[k]的位置。

对第三点的说明:
KMP的一个巧妙的地方在于,它利用我们上面用B匹配A的方法来计算F数组,简单点来说,就是用B串匹配B串自己!当然,因为B串==B串,所以如果直接按上面的匹配,那是毫无意义的,所以这里要变一变。
3.6 next数组的图解过程
现在,我们再看一下如何编程快速求得next数组。其实,求next数组的过程完全可以看成字符串匹配的过程,即以模式字符串为主字符串,以模式字符串的前缀为目标字符串,一旦字符串匹配成功,那么当前的next值就是匹配成功的字符串的长度。
具体来说,就是从模式字符串的第一位(注意,不包括第0位)开始对自身进行匹配运算。 在任一位置,能匹配的最长长度就是当前位置的next值。如下图所示(参考:如何更好地理解和掌握 KMP 算法? - 海纳的回答 - 知乎 ):
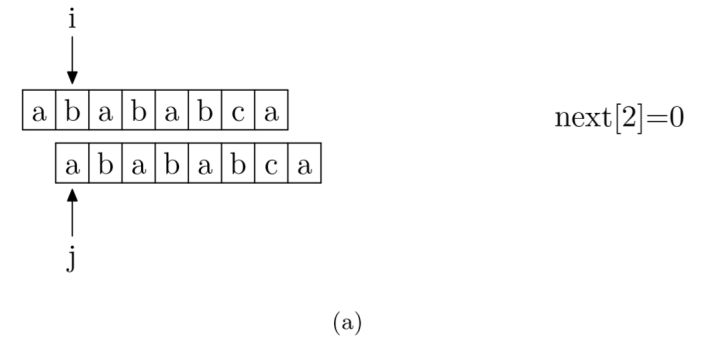
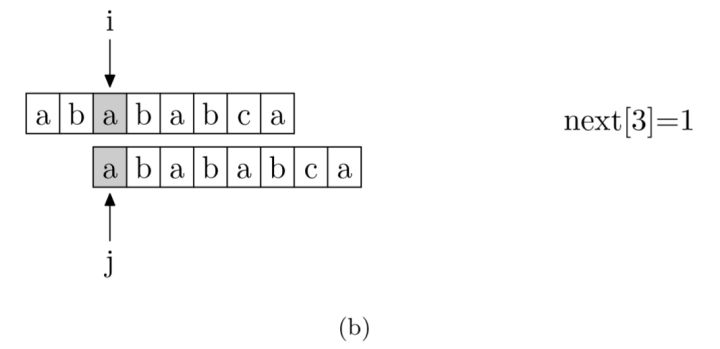

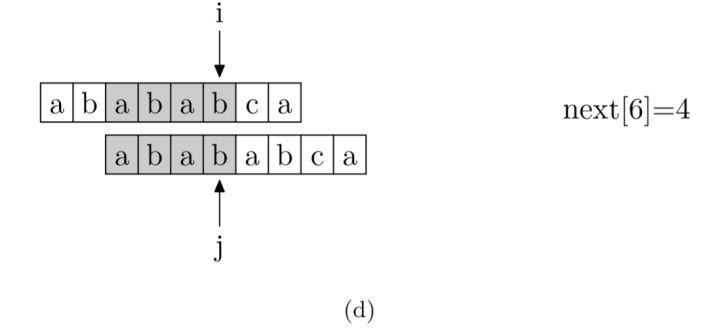
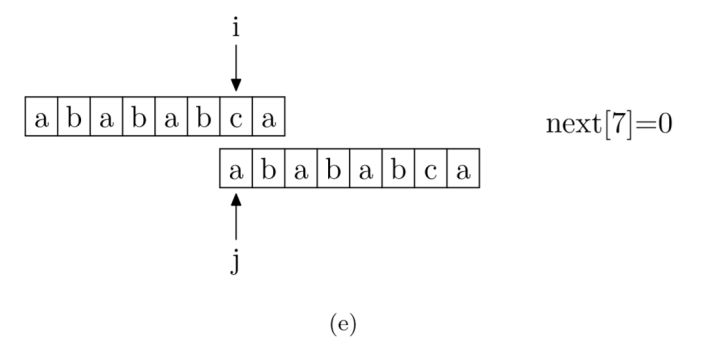
在举个例子,以上述字符串"ABCDABD"为例
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 模式串 | A | B | C | D | A | B | D |
| next[i] | -1 | 0 | 0 | 0 | 0 | 1 | 2 |
-
- i = 0,对于模式串的首字符,我们统一为next[0] = -1;
- i = 1,前面的字符串为A,其最长相同前后缀长度为 0,即next[1] = 0;
- i = 2,前面的字符串为AB,其最长相同前后缀长度为 0,即next[2] = 0;
- i = 3,前面的字符串为ABC,其最长相同前后缀长度为 0,即next[3] = 0;
- i = 4,前面的字符串为ABCD,其最长相同前后缀长度为 0,即next[4] = 0;
- i = 5,前面的字符串为ABCDA,其最长相同前后缀为A,即next[5] = 1;
- i = 6,前面的字符串为ABCDAB,其最长相同前后缀为AB,即next[6] = 2;
- i = 7,前面的字符串为ABCDABD,其最长相同前后缀长度为 0,即next[7] = 0。
3.7 代码
def getNext(pattern):
nextArr = []
if len(pattern) == 1:
return [-1]
lens = len(pattern)
nextArr = [-1 for _ in range(lens)]
nextArr[0] = -1
nextArr[1] = 0
i = 2 # next数组的位置
k = 0
while i < lens:
if pattern[i - 1] == pattern[k]:
# 如果当前位置字符相同,位置加一,并且更新当前位置nextArr值
k += 1
nextArr[i] = k
i += 1
elif k > 0:
# 如果当前位置字符不相同,前位置最长相同前后缀,继续匹配
k = nextArr[k]
else:
# 否则 更新值为0,i更新+1
nextArr[i] = 0
i += 1
return nextArr
def kmp(text, pattern):
if not text or not pattern or len(text) < len(pattern):
return -1
i1 = 0 # text当前匹配位置
i2 = 0 # pattern当前匹配位置
nextArr = getNext(pattern)
while i1 < len(text) and i2 < len(pattern):
if text[i1] == pattern[i2]:
# 若当前字符匹配,位置加一
i1 += 1
i2 += 1
elif nextArr[i2] == -1:
# pattern位置来到开头,没有则text位置往后挪一位,重新匹配
# 相当于第11步
i1 += 1
else:
# nextArr[i2],返回当前位置最长相同前后缀,从此位置继续匹配
# 相当于第9步
i2 = nextArr[i2]
if i2 == len(pattern):
return i1 - i2
return -1
if __name__ == '__main__':
text = "BBC ABCDAB ABCDABCDABDE"
pattern = "ABCDABD"
index = kmp(text, pattern)
print(index)






