NOI十连测 第三测 T1
这么二逼的题考试的时候我想了好久，我真是太弱了。。。
首先，由于ans都乘上了i*(i-1)/2，实际上要求的就是每个数的所有可能出现次数*这个数的权值。
我们发现，每个数的本质是一样的，我们记一个sum为数的总和，这样只要统计一次就OK了。
我们把每次的选择抽象成有向边，每个状态视为点，这样就构成一个有根树。
如图
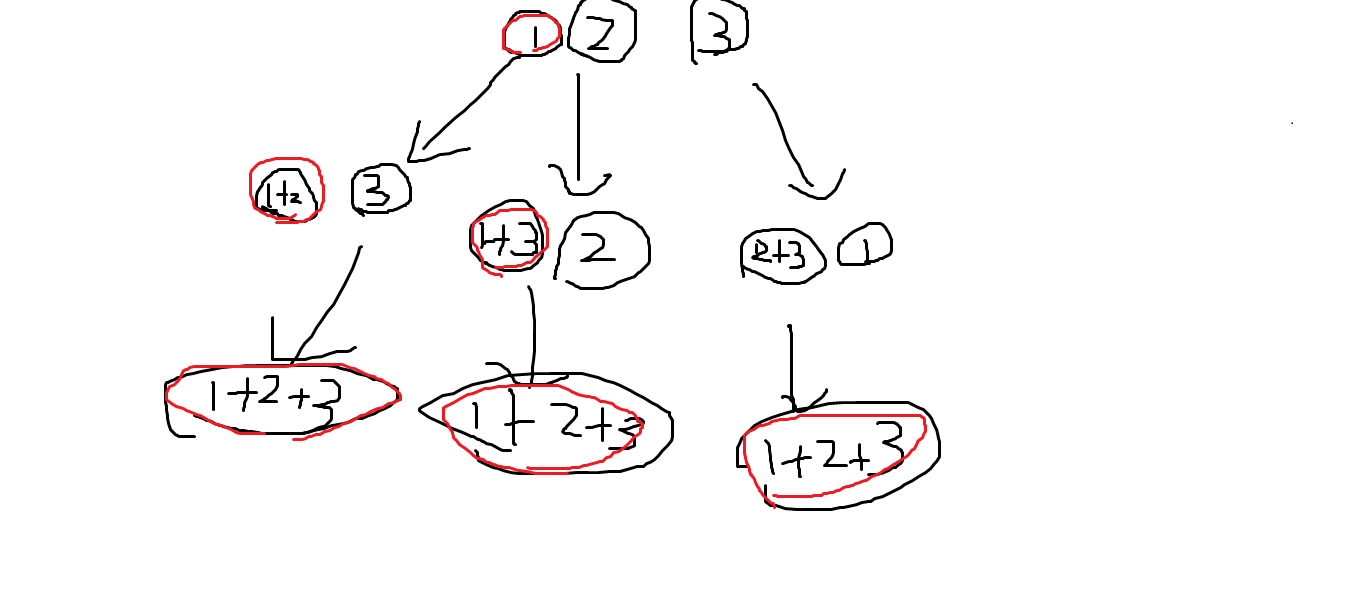
我们只考虑1对答案的贡献。如图，在每层计算当前合并对答案的贡献，也就是要能得知我在这个节点选择合并1或者1的联通块，那么我能覆盖到几个叶子节点？
那么就变成O(n)的组合数学题了。。对了，组合数用到的阶乘和阶乘逆元可以O(n)预处理。
1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<cstring> 5 #include<algorithm> 6 #define ll long long 7 int ans=0,a[200005],n,cnt[20],size[20]; 8 const ll Mod=1000000007; 9 ll sum,jcny[200005],jc[200005],f[200005],son[200005],Num[200005]; 10 int read(){ 11 int t=0,f=1;char ch=getchar(); 12 while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();} 13 while ('0'<=ch&&ch<='9'){t=t*10+ch-'0';ch=getchar();} 14 return t*f; 15 } 16 bool cmp(const int &a,const int &b){ 17 return a>b; 18 } 19 ll gcd(ll a,ll b){ 20 if (b==0) return a; 21 else return gcd(b,a%b); 22 } 23 void exgcd(ll a,ll b,ll &x,ll &y){ 24 if (b==0){ 25 x=1;y=0; 26 return; 27 } 28 exgcd(b,a%b,x,y); 29 ll t=x; 30 x=y; 31 y=t-(a/b)*y; 32 } 33 void init(){ 34 jc[0]=1;jcny[0]=1; 35 for (ll i=1;i<=n+1;i++) jc[i]=(jc[i-1]*i)%Mod; 36 ll x,y; 37 exgcd(jc[n+1],Mod,x,y); 38 jcny[n+1]=(x%Mod+Mod)%Mod; 39 for (int i=n;i>=1;i--) jcny[i]=(jcny[i+1]*(i+1))%Mod; 40 } 41 ll C(int n,int m){ 42 return (((jc[n]*jcny[m])%Mod)*jcny[n-m])%Mod; 43 } 44 int dfs(int x1,int x2,int x3,int x4,int x5,int num,int res){ 45 int b[5]; 46 int Res=1; 47 if (num==1){ 48 ans=(ans+res)%Mod; 49 return Res; 50 } 51 b[0]=x1;b[1]=x2;b[2]=x3;b[3]=x4;b[4]=x5; 52 std::sort(b,b+num,cmp); 53 for (int i=0;i<num;i++) 54 for (int j=i+1;j<num;j++){ 55 b[i]+=b[j];int tmp=b[j];b[j]=0;std::swap(b[j],b[num-1]); 56 Res+=dfs(b[0],b[1],b[2],b[3],b[4],num-1,(res+b[i])%Mod); 57 std::swap(b[j],b[num-1]); 58 b[i]-=tmp;b[j]=tmp; 59 } 60 return Res; 61 } 62 ll inv(ll a){ 63 ll x,y; 64 exgcd(a,Mod,x,y); 65 return x; 66 } 67 void sbpianfen(){ 68 int k=dfs(a[1],a[2],a[3],a[4],a[5],n,0); 69 printf("%d\n",ans); 70 } 71 ll A(int n,int m){ 72 return (jc[n]*jcny[n-m])%Mod; 73 } 74 ll Pow(ll x,ll y){ 75 ll res=1; 76 while (y){ 77 if (y%2) res=(res*x)%Mod; 78 x=(x*x)%Mod; 79 y/=2; 80 } 81 return res; 82 } 83 void sxpianfen(){ 84 ll res=0; 85 son[1]=1;son[0]=1; 86 for (int i=2,num=n;i<=n;i++,num--) 87 son[i]=(son[i-1]*C(num,2))%Mod;//这行 88 Num[n-1]=1;Num[n]=1;Num[n+1]=1;Num[n+2]=1; 89 for (int i=n-2,num=2;i>=1;i--,num++) 90 Num[i]=(Num[i+1]*C(num+1,2))%Mod; //叶子 91 for (int i=1,num=n;i<=n-1;i++,num--){ 92 res=(res+(son[i]*Num[i+1])%Mod*(num-1))%Mod; 93 } 94 res=(res*sum)%Mod; 95 printf("%lld\n",res); 96 } 97 int main(){ 98 n=read();init(); 99 for (int i=1;i<=n;i++) 100 a[i]=read(),sum=(sum+a[i])%Mod; 101 if (n<=5){sbpianfen();return 0;} 102 if (n<=100000){sxpianfen();return 0;} 103 }
