「数形结合」- 斜率优化 DP
下面用例题来具体阐释斜率优化的思想。
例 1：P2365 任务安排
题目大意：有 \(n\) 个任务要在一台机器上依次完成，现在要将其划分为若干段，每一段中的任务同时完成，且在每一段开始前需要启动时间 \(s\)。第 \(i\) 个任务消耗 \(t_i\) 的时间，在 \(T\) 时刻完成需要消耗 \(c_i\times T\) 的费用。求完成所有任务的最小费用。\(n\le 5000\)。
我们先考虑推出最朴素的方程式。假设 \(f_{i,j}\) 表示前 \(i\) 个任务划分为 \(j\) 段的最小费用，则转移方程式为：\(f_{i,j} = \min\limits_{k=j-1}^{i-1}\{f_{k,j-1}+(s\times j + \sum_{p=1}^{i}t_p)\times\sum_{p=k+1}^i c_i\}\)。使用前缀和 \(sumt_i=\sum_{p=1}^i t_i\)，\(sumc_i=\sum_{p=1}^i c_i\)，得到 \(f_{i,j} = \min\limits_{k=j-1}^{i-1}\{f_{k,j-1}+(s\times j + sumt_i)\times(sumc_i - sumc_k)\}\)。发现我们并不需要关注到底划分为了几段，而之前分的段对之后的时间恒有 \(s\) 的贡献，于是我们可以 “预支” 这些时间，将费用提前计算，设前 \(i\) 项任务的最小费用为 \(f_i\)，可以得到：
此时复杂度是 \(\mathcal{O}(n^2)\) 的，足以通过此题。
#include<iostream>
#include<cstdio>
#define maxn 5005
#define inf 50000000005
#define ll long long
using namespace std;
int n,s,ti[maxn],co[maxn]; ll f[maxn];
int main(){
scanf("%d%d",&n,&s); for(int i=1;i<=n;i++)
scanf("%d%d",&ti[i],&co[i]),ti[i]+=ti[i-1],co[i]+=co[i-1],f[i]=inf;
for(int i=1;i<=n;i++) for(int j=0;j<i;j++)
f[i]=min(f[i],f[j]+1LL*ti[i]*(co[i]-co[j])+1LL*s*(co[n]-co[j]));
printf("%lld",f[n]);
return 0;
}
假如 \(n\le 3\times 10^5\) 呢？此时我们可以采用斜率优化。将刚刚的 DP 方程式改写一下：
对于某一个确定的 \(j\)，我们可以把 \(\min\) 脱掉，移项得到：
这时，我们发现，可以把这个式子看作是直线 \(y=kx + b\) 的形式，即：\(f_j = k\times sumc_j+b\)，其中 \(\begin{cases}k=sumt_i + s\\b=f_i - sumt_i\times sumc_i - s\times sumc_n\end{cases}\)。于是，对于确定的 \(j\)，我们可以找到对应的点 \((sumc_j,f_j)\)，过这个点作一条斜率为 \(sumt_i + s\) 的直线，纵截距就是 \(f_i - sumt_i\times sumc_i - s\times sumc_n\)。我们想要找到最小的 \(f_i\)，就是想要找到最小的截距，于是，我们可以用斜率为 \(sumt_i + s\) 的直线自下而上逼近，得到的第一个点就是想要的 \(j\)。
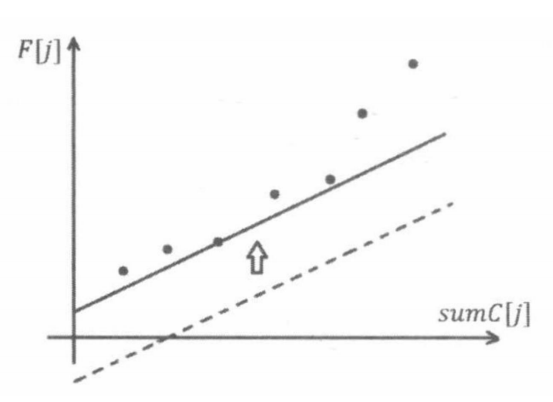
此时，我们就可以发现，能成为决策点的点一定在下凸壳上。于是，我们只需要维护这样一个下凸壳，就能及时排除一些无用的决策点，例如下图（下记 \(k_{i,j}\) 为 \((sumc_i,f_i)\) 和 \((sumc_j,f_j)\) 之间的斜率，即 \(k_{i,j} = \frac{f_j-f_i}{sumc_j-sumc_i}\)）：
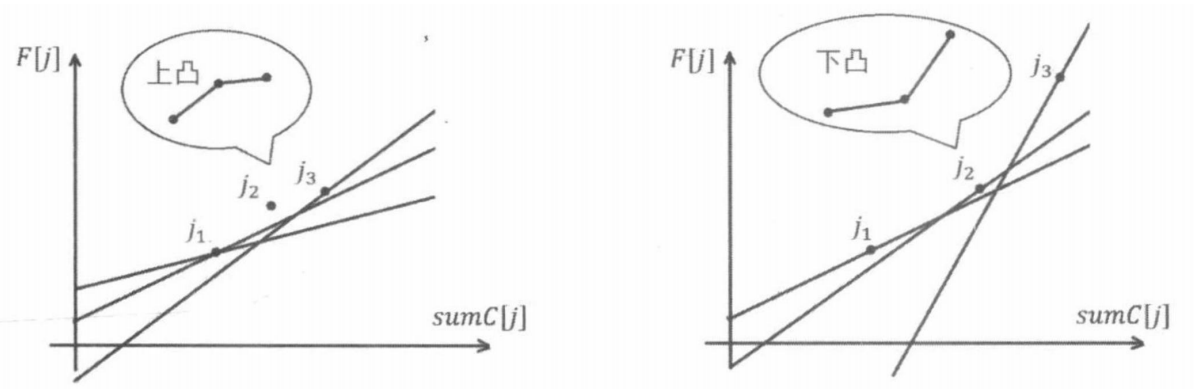
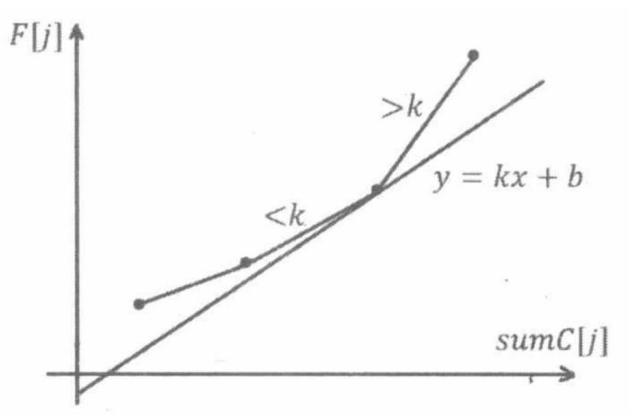
如左图，由于 \(k_{j_1\,,\,j_2} > k_{j_2\,,\,j_3}\)，于是 \(j_2\) 永远不可能作为决策点，也就是说，所有这样满足 \(k_{j_1\,,\,j_2} < k_{j_2\,,\,j_3}\) 的 \(j_2\) 我们都是不需要的。
又因为我们要求的斜率 \(k=sumt_i + s\) 是单调递增的，于是可以用一个单调队列来维护这一个下凸壳，就能解决问题。
#include<iostream>
#include<cstdio>
#define maxn 5005
#define inf 50000000005
#define ll long long
using namespace std;
int n,s,ti[maxn],co[maxn],q[maxn],l=1,r=1; ll f[maxn];
int main(){
scanf("%d%d",&n,&s); for(int i=1;i<=n;i++)
scanf("%d%d",&ti[i],&co[i]),ti[i]+=ti[i-1],co[i]+=co[i-1],f[i]=inf;
for(int i=1;i<=n;i++){
while(l<r&&1LL*(f[q[l+1]]-f[q[l]])<=1LL*(s+ti[i])*(co[q[l+1]]-co[q[l]])) l++;
f[i]=f[q[l]]+1LL*ti[i]*co[i]+1LL*s*co[n]-1LL*(s+ti[i])*co[q[l]];
while(l<r&&1LL*(f[i]-f[q[r]])*(co[q[r]]-co[q[r-1]])<=1LL*(f[q[r]]-f[q[r-1]])*(co[i]-co[q[r]])) r--;
q[++r]=i;
} printf("%lld",f[n]);
return 0;
}
P5785 [SDOI2012] 任务安排
题目大意：同例 1，但是 \(t_i\) 可以是负数（不要管有没有现实意义）。
那么，此时斜率 \(k = sumt_i + s\) 不具有单调性，所以我们单调队列的队头就不用向前推进了，也就是退化为单调栈。所以，我们在单调栈上二分查找这个决策点即可。
#include<iostream>
#include<cstdio>
#define maxn 300005
#define inf 50000000005
#define ll long long
using namespace std;
int n,s,ti[maxn],co[maxn],st[maxn],r=1; ll f[maxn];
int bi_search(int l,int r,ll k){
int res=r; while(l<=r){
int mid=(l+r)>>1;
if(1LL*(f[st[mid+1]]-f[st[mid]])>=1LL*k*(co[st[mid+1]]-co[st[mid]])) res=mid,r=mid-1; else l=mid+1;
} return res;
}
int main(){
scanf("%d%d",&n,&s); for(int i=1;i<=n;i++)
scanf("%d%d",&ti[i],&co[i]),ti[i]+=ti[i-1],co[i]+=co[i-1],f[i]=inf;
for(int i=1;i<=n;i++){
int pos=bi_search(1,r,1LL*(ti[i]+s));
f[i]=f[st[pos]]+1LL*ti[i]*co[i]+1LL*s*co[n]-1LL*(s+ti[i])*co[st[pos]];
while(r>1&&1LL*(f[i]-f[st[r]])*(co[st[r]]-co[st[r-1]])<=1LL*(f[st[r]]-f[st[r-1]])*(co[i]-co[st[r]]))
r--;
st[++r]=i;
} printf("%lld",f[n]);
return 0;
}
