网格图建模

本文仅介绍遇到网格图时的一些思考方向及方法。遇到网格图时，多将其转化为图论问题，后使用最短路/二分图/网络流等进行求解。

黑白染色

网格图的黑白染色可以帮助我们解决一类问题。

例如，有一个 \(n\times m\) 的网格（\(n,m\) 均为奇数），现在想在其中放置若干 \(1\times 2\) 的骨牌，显然会空一格，那么，空的这一格 \((x,y)\) 有什么特征呢？显然，任意 \((x,y)\)（\(x,y\) 均为奇数）都符合条件。不难证明：将原网格图黑白染色，\((1,1)\) 染黑色，\((1,2)\) 染白色，……发现黑色格子比白色格子多一块。又因为每一块骨牌必定覆盖在一格黑色格子和一格白色格子上面，于是最后空出来的一定是一格黑色格子，即满足 \(x,y\) 均为奇数的 \((x,y)\)，对于任意一个这样的 \((x,y)\)，显然都能构造出一种覆盖方案。

又如，一个网格里每格都填上了一个数，现在可以分别让每个格子的数加一或不变，那么对于所有的初始网格，是否总存在一种方案使得任意两个相邻的数都不同呢？答案是正确的。我们对网格进行黑白染色，那么，相邻的数都在不同颜色的格子上，此时我们将这些数分成了两类。考虑加一能起到的效果，我们可以将颜色与奇偶性相对应，例如可以把黑色格子上的数全部变成奇数，白色格子上的数全部变成偶数，那么相邻的数就不可能相同了。

例 1：CF1753D The Beach

题目大意：\(n\times m\) 的网格上有若干个不可移动的障碍和若干 \(1\times 2\) 的沙滩椅，可以花 \(p\) 的代价将一个沙滩椅绕一端旋转 \(90^\circ\)，或花 \(q\) 的代价将一个沙滩椅绕一端旋转 \(180^\circ\)，求空出一个 \(1\times 2\) 的空位所需要花费的最小代价。

对网格进行黑白染色，一个沙滩椅所覆盖的格子必定一黑一白，且操作的一个格子颜色始终不变。于是对两种颜色分别建图，跑一遍多源最短路找最小值即可。

例 2：CF316C2 Tidying Up

题目大意：有一个 \(n\times m\) 的鞋柜，其中摆满了若干双鞋，一个格子内只有一只鞋，现在要将若干鞋子同时拿出，在再分别把他们放仅、进某个位置。求操作后同一双鞋的两只都相邻所需要拿出的最小鞋子数。

对图进行黑白染色，一双鞋要相邻故一定是一只在黑色格子上另一只在白色格子上。于是，对每一个格子向周围连边，是否已经匹配作为边权 \(0\) 或 \(1\)，跑一遍二分图最小权完美匹配即可。

建图（建模）

例 3：P6545 [CEOI2014] The Wall

题目大意：在一个 \(n\times m\) 的网格里，有若干格子里是城市，现在要沿着网格边线建造连续的城墙，每一条边线有代价，求城墙围住所有城市且进过左上角 \((0,0)\) 的最小代价。

引理：假设 \(u\rightarrow v\) 的最短路经过 \(w\)，则这条最短路中 \(u\rightarrow w\) 的路径一定是 \(u\) 和 \(w\) 间的最短路径。正确性显然。

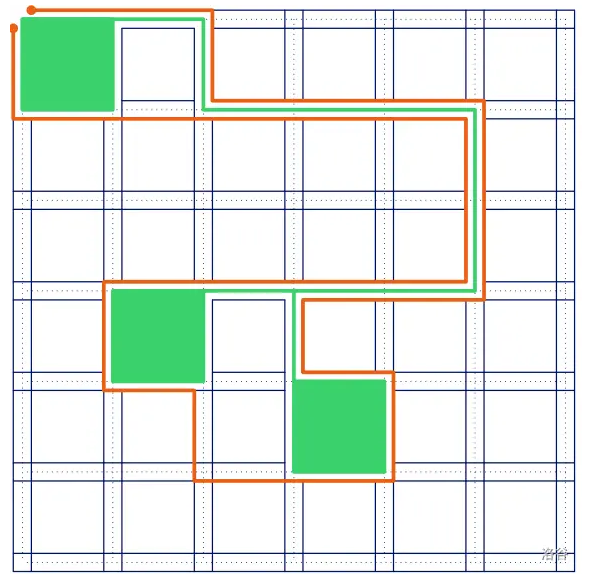
根据引理，最终城墙一定围住了 \((0,0)\) 到各个城市所在格子的左上角的各条路径，城墙不能“穿过”这些最短路。我们可以讲每个点拆成四个，用边权为 \(0\) 的遍相连，分别从属于四周的四个格子，将最短路穿过的边删掉，然后跑最短路即可。如下图（来源于洛谷题解区）：

平面图欧拉定理

定理内容：如果一个连通平面图有 \(v\) 个顶点、\(e\) 条边、\(f\) 个面，则 \(v-e+f = 2\)。

例 4：P3776 [APIO2017] 斑斓之地

题目大意：有一个 \(n\times m\) 的网格，其中有一些黑格子，构成了一个联通块。多次询问一个子网格内有多少个白格子构成的极大连通块。

根据欧拉公式，可以推出：连通块数 = 点数 \(-\) 边数 \(+\) 面数 \(- 1\)。

那么，对每个白色格子建一个点，相邻的白色格子对应的点连边。查询子网格时，找到对应的点数、边数以及面数即可。