凸包

叉积

众所周知，向量 \(\vec{a}\) 和 \(\vec{b}\) 的数量积（或点积、内积）为 \(\vec{a}\cdot \vec{b} = |\vec{a}||\vec{b}|\cos\theta\)（其中 \(\theta = <\vec{a},\vec{b}>\)）。

类似地，向量存在向量积（或叉积、外积），定义为：向量 \(\vec{a}\) 与 \(\vec{b}\) 的叉积是一个向量，其模 \(|\vec{a}\times \vec{b}| = |\vec{a}||\vec{b}|\sin\theta\)，方向与 \(\vec{a}\) 和 \(\vec{b}\) 都垂直，且符合右手法则。

叉积的几何意义是，其模长等于 \(\vec{a}\) 和 \(\vec{b}\) 以邻边构成的平行四边形面积。

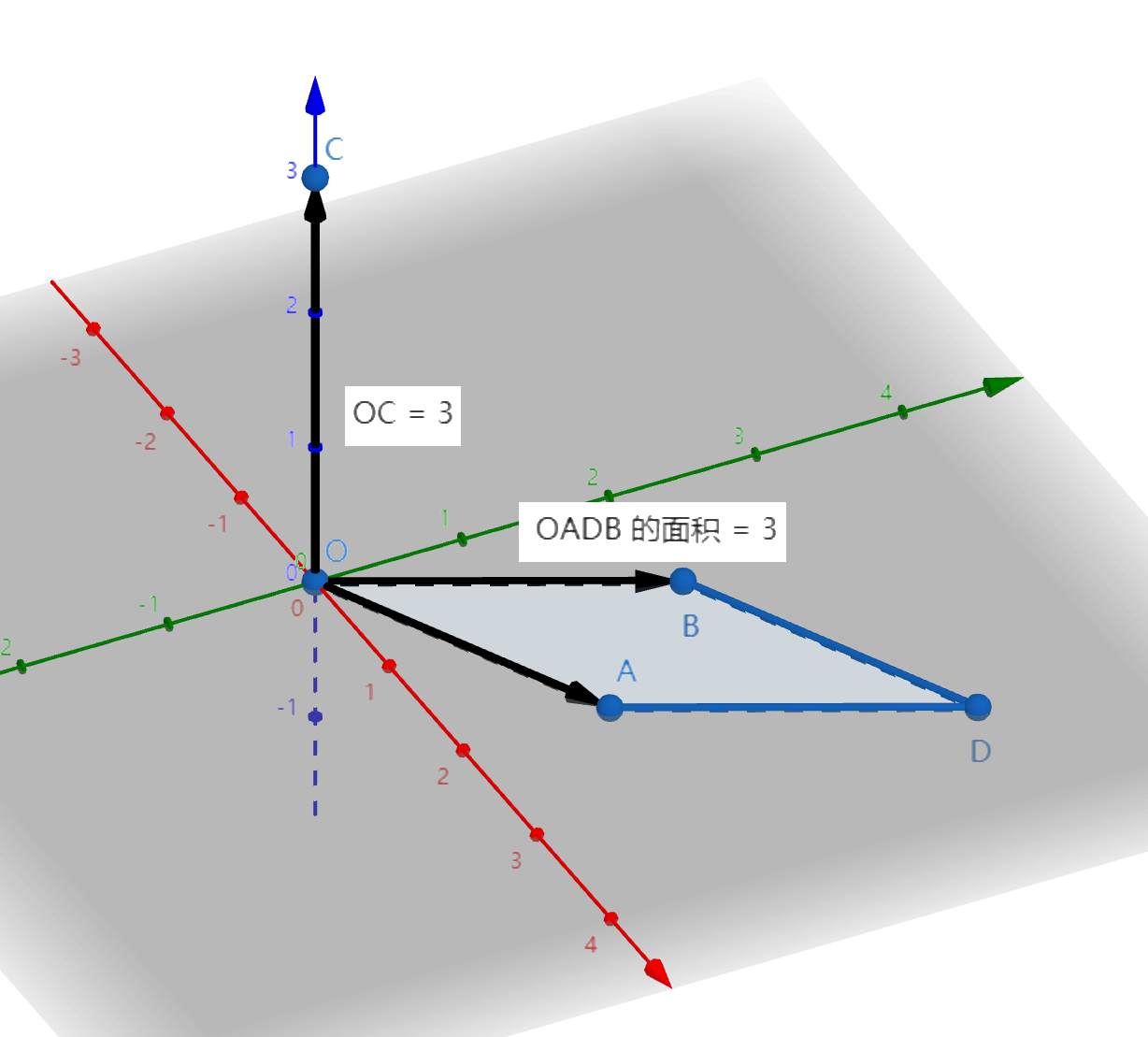
同时，我们可用叉积的正负来判断点在直线的哪一侧。假设我们利用 \((P,\vec{u})\)（直线上一点加上表示方向的向量）来表示一条直线。那么，对于一点 \(Q\)，若 \(\vec{PQ}\times \vec{u}>0\)，则 \(Q\) 在直线左侧（或下侧），否则若 \(\vec{PQ}\times \vec{u}<0\) 则在右侧（或上侧），否则在直线上。

极坐标系

在航海中，常常运用例如“北偏东 \(30^\circ\ 200m\) 处”来表示方位。像这样，以一点 \(O\) 为极点，\(Ox\) 为极轴，再选择正方向及单位长度就形成了极坐标系。

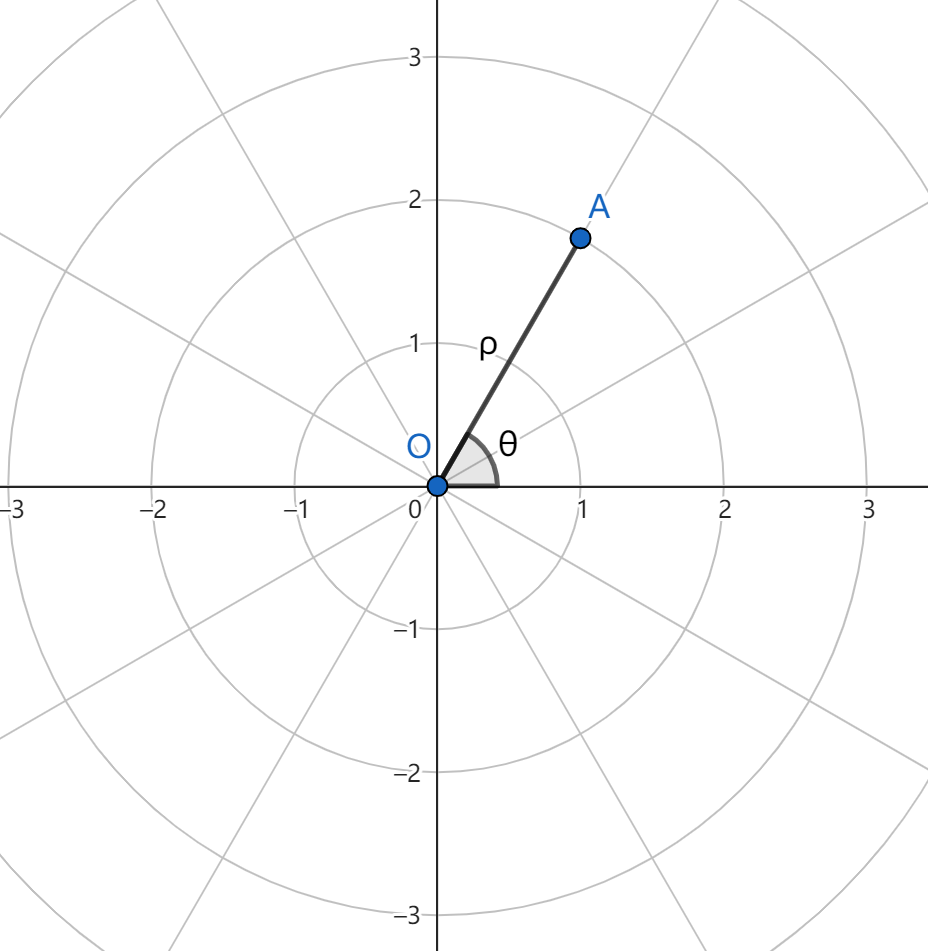
极坐标系中，点 \(A\) 的位置由其到极点的距离极径 \(|OA| = \rho\) 以及极角 \(\angle{xOA} = \theta\) 决定，故 \(A\) 的坐标可表示为 \((\rho,\theta)\)。

平面直角坐标系和极坐标系的坐标转换可表示为 \(\begin{cases}x = \rho\cos\theta \\ y = \rho\sin\theta \end{cases}\)，所以 \(\rho^2 = x^2 + y^2\)，\(\theta = \arctan\dfrac{y}{x}(x\neq 0)\)。在 \(\texttt{cmath}\) 中，有 \(\operatorname{atan2}(y,x)\) 函数来计算 \(\theta\)。

凸包

凸多边形

凸多边形即所有内角大小均在 \([0,\pi]\) 之间的多边形，所有点都在任意一条边所在的直线同侧，任意两点间连线不在凸多边形外。

凸包

给定集合 \(X\)，所有包含 \(X\) 的凸集的交集 \(S\) 称为 \(X\) 的凸包。在平面内，可以看作是用一根橡皮筋包含所有的点时的形态。

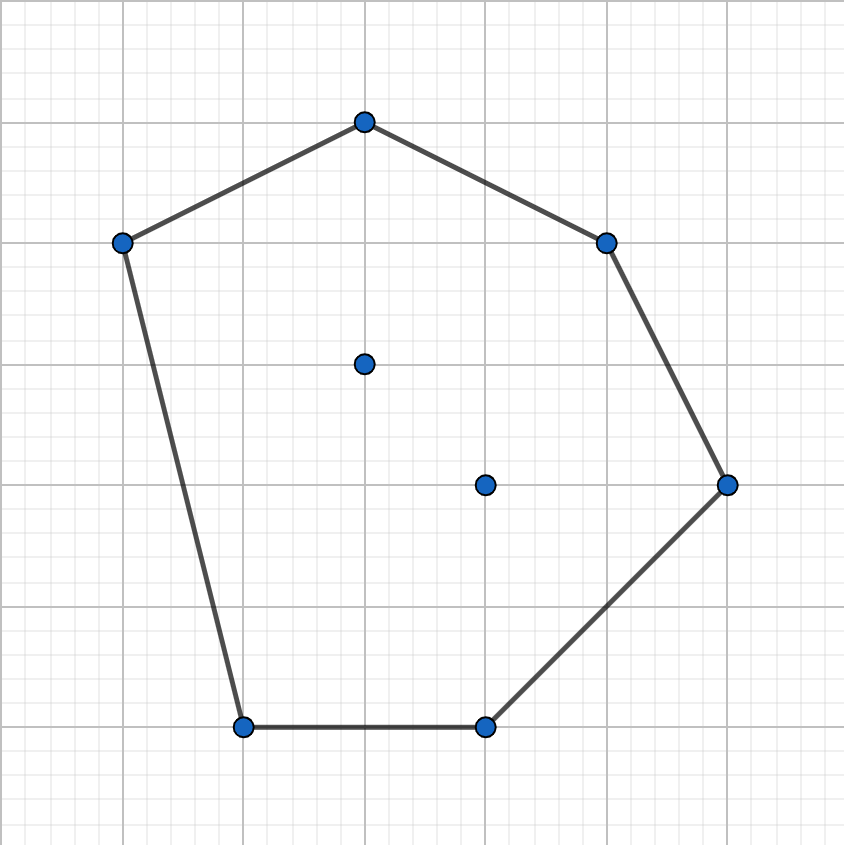
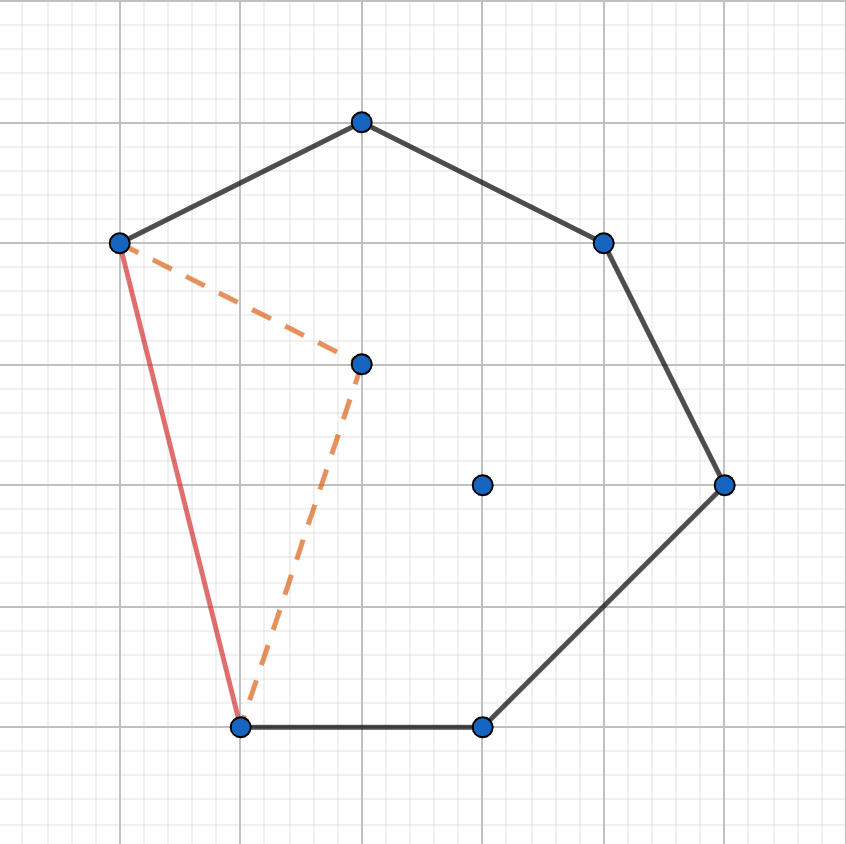
凸包是包住所有给定点的图形中周长最小的。若是凹多边形，如下图，根据三角形任意两边之和大于第三边，橙色部分周长不如红色部分。

求解凸包

Jarvis算法

首先从任意一点 \(A\) 开始，任意作一条直线 \(s\)，使得所有点在 \(s\) 同侧，将 \(A\) 与所有点连线，找到 \(\angle{BAs}\) 最小的点 \(B\)，\(AB\) 就是凸包上的一条边。

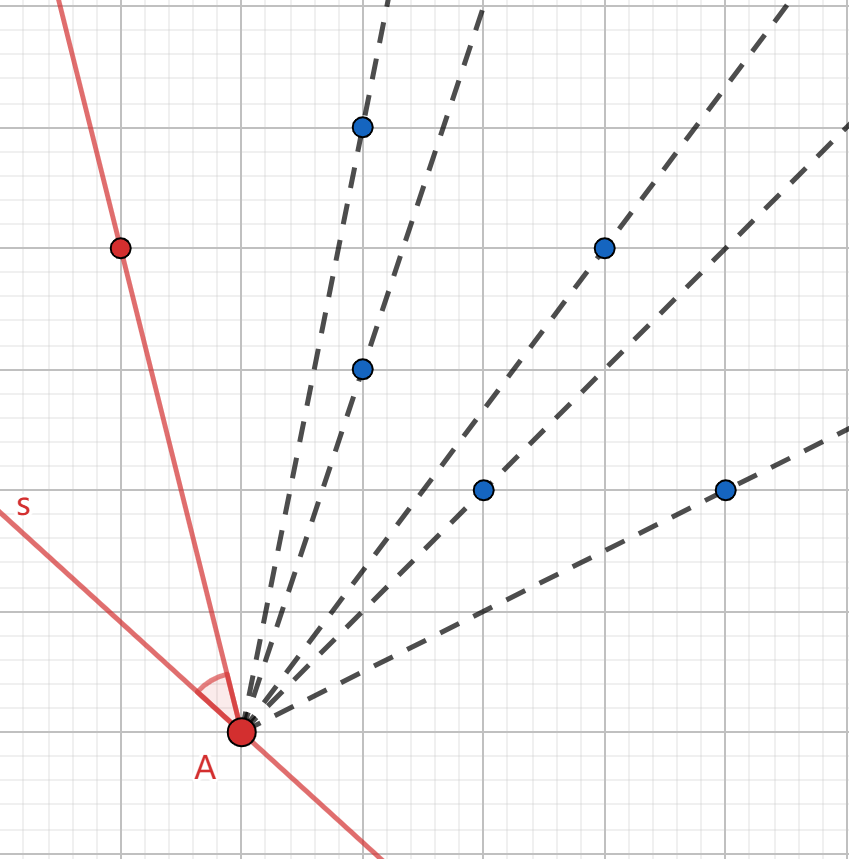
然后以 \(B\) 为上一步中的 \(A\)，重复这一过程，得到凸包。

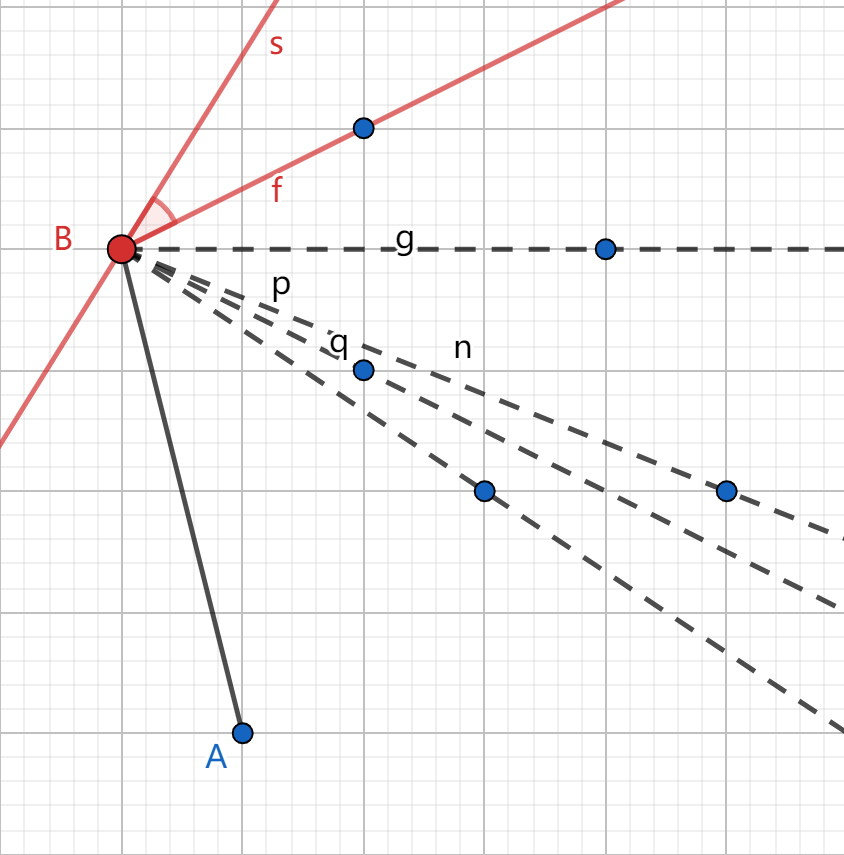
但是，这一过程的复杂度显然很高，为 \(\mathcal{O}(nm)\) 级别（\(n\) 为点数，\(m\) 为凸包上点数），所以还要考虑更优的方法。

Graham算法

首先从 \(y\) 值最小的点 \(A\) 开始，找到剩余点中极角最小的一个入栈，用类似单调栈的方法维护栈中点的凸性。

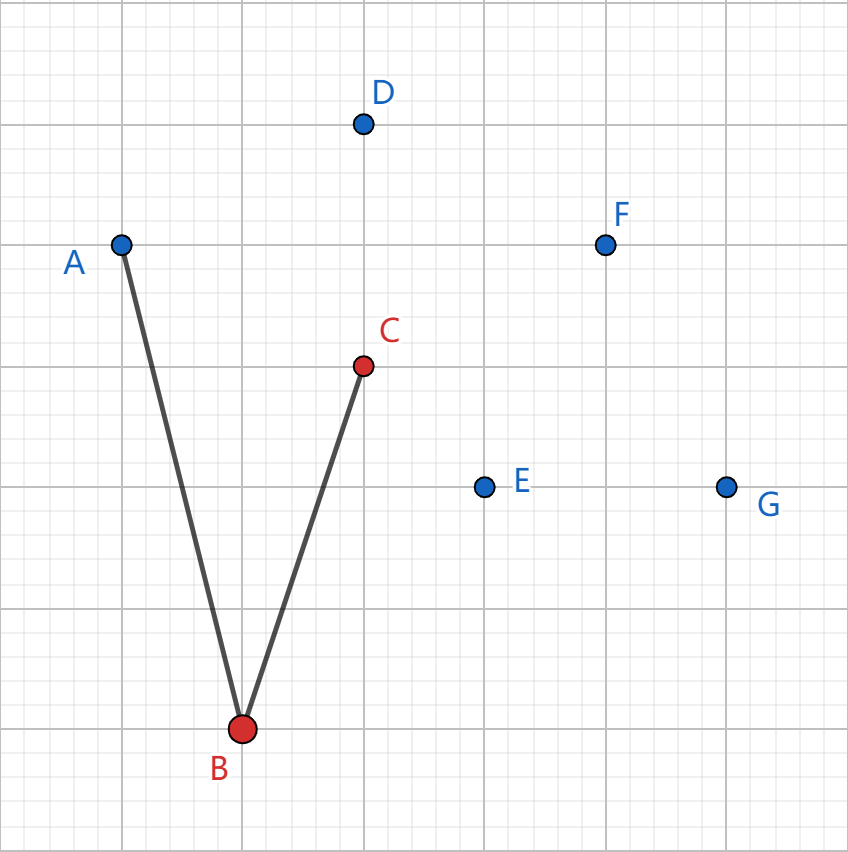
以上图举例子，以 \(A\) 为极点，将所有点排序（图中 \(A\sim G\)）。找到极角最小的点 \(B\) 入栈。

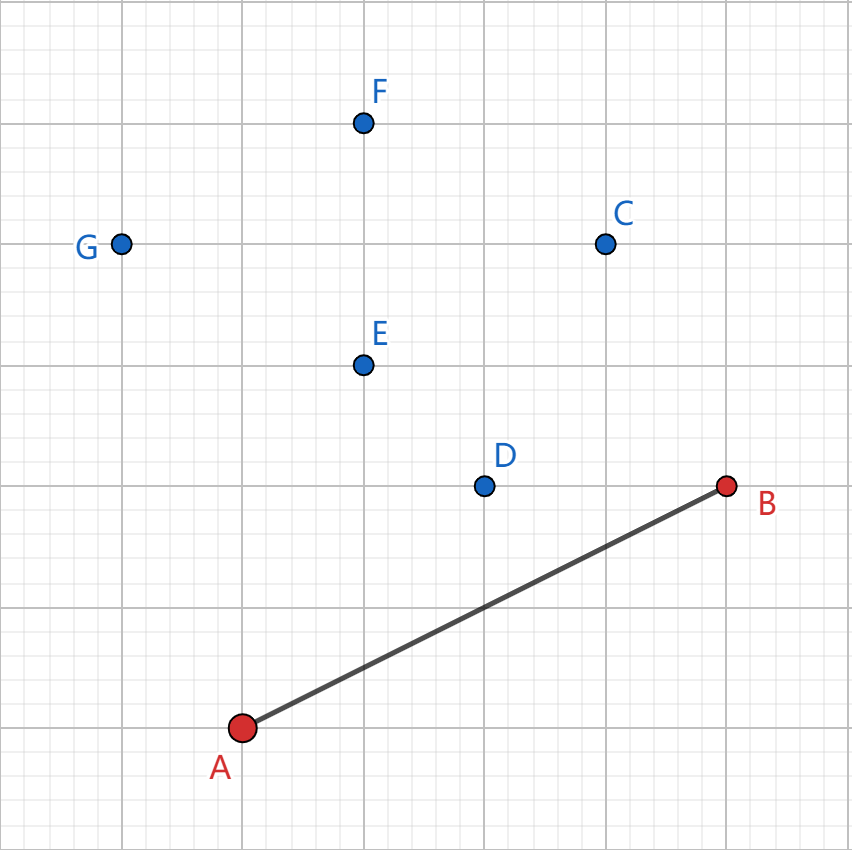
再将 \(C\) 入栈：

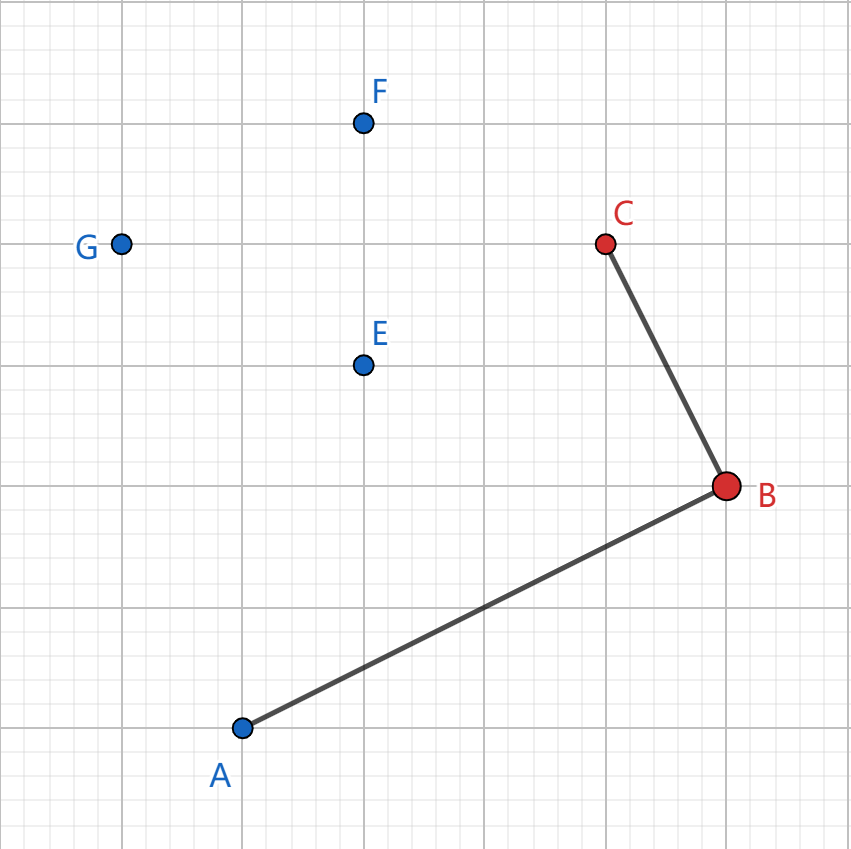
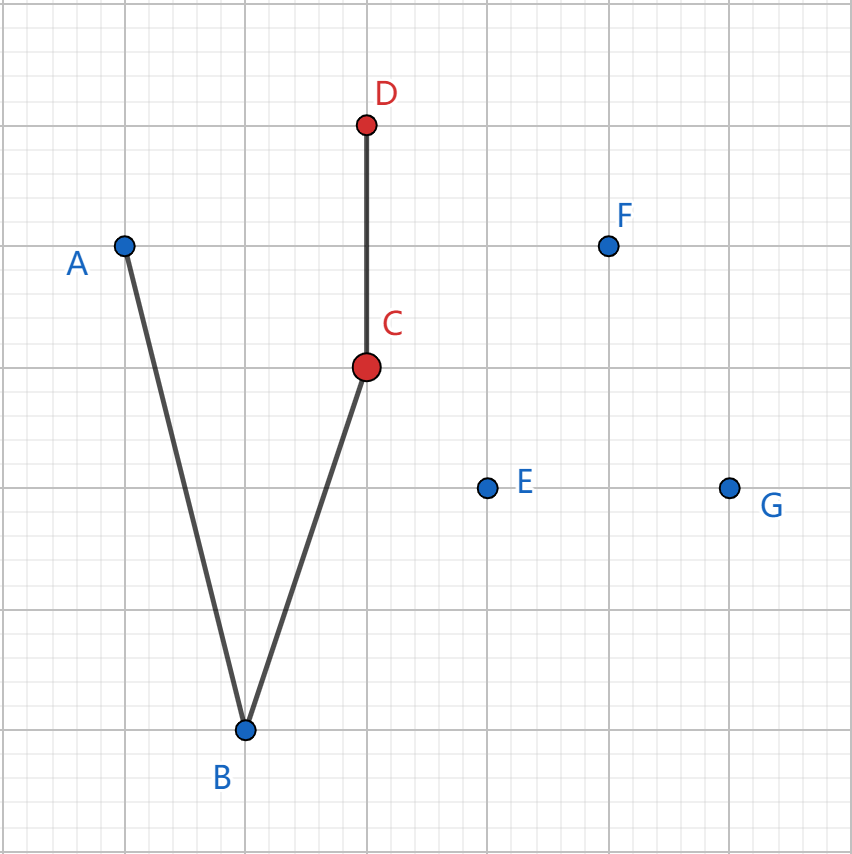
然后是 \(D\)：

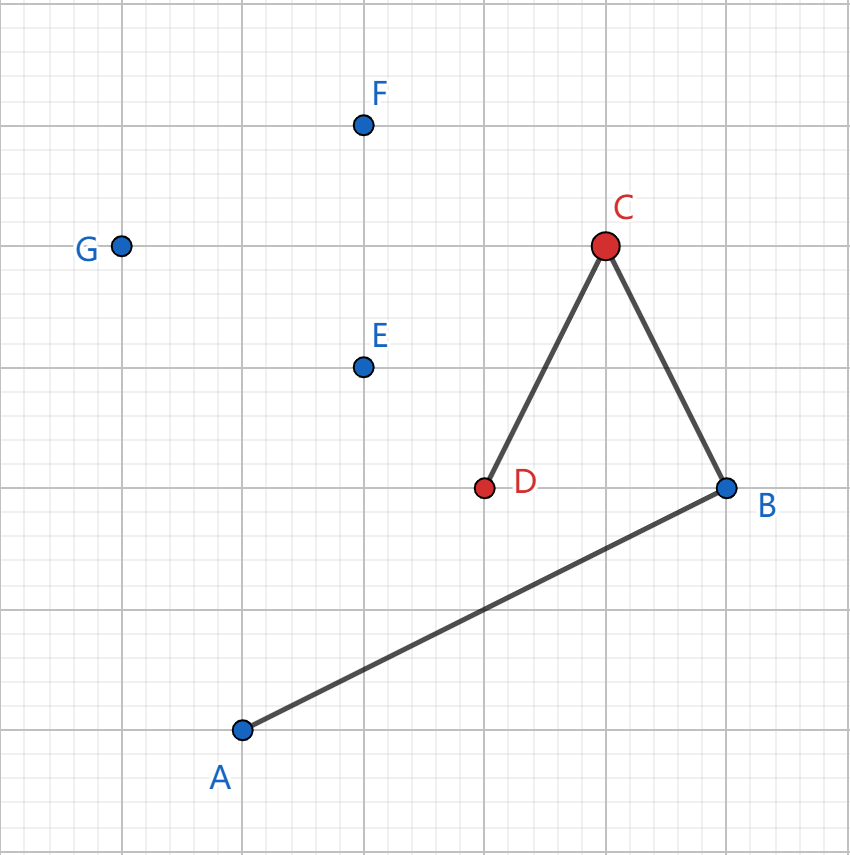
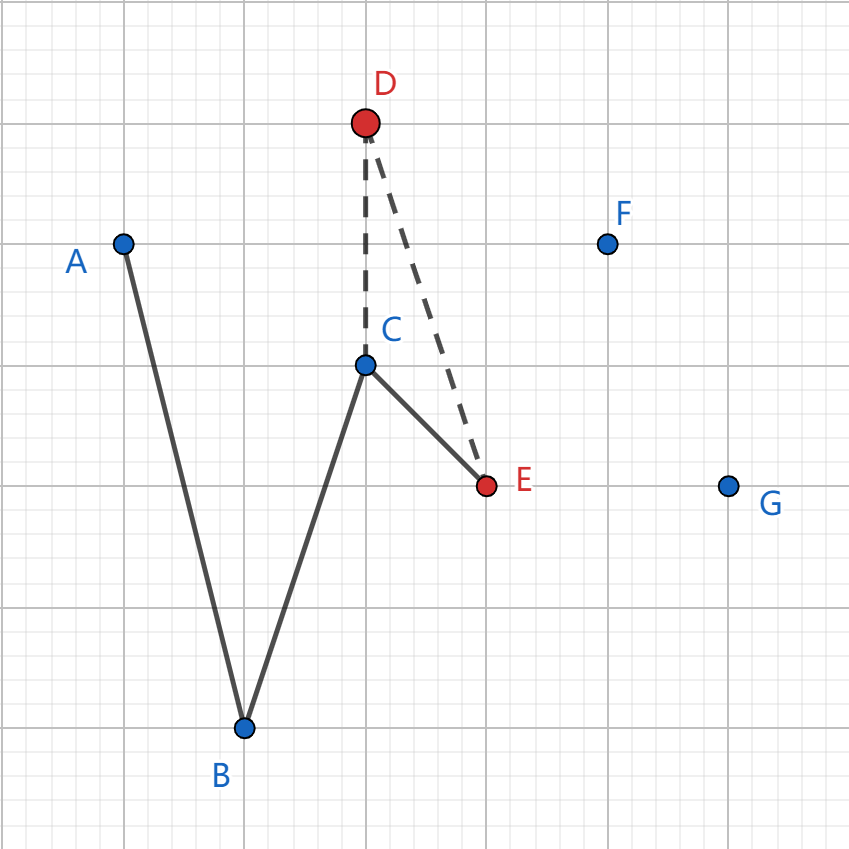
\(E\) 入栈时，发现其在栈顶的直线 \(CD\) 右侧，弹出栈顶 \(D\)；\(E\) 在栈顶的直线 \(BC\) 左侧，可以入栈：

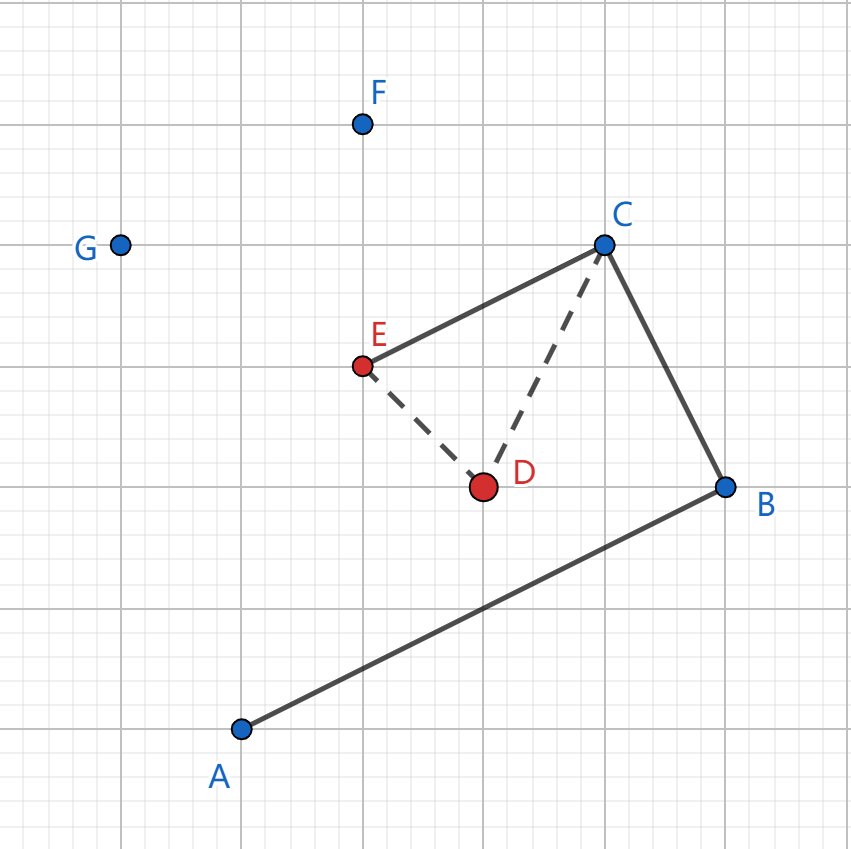
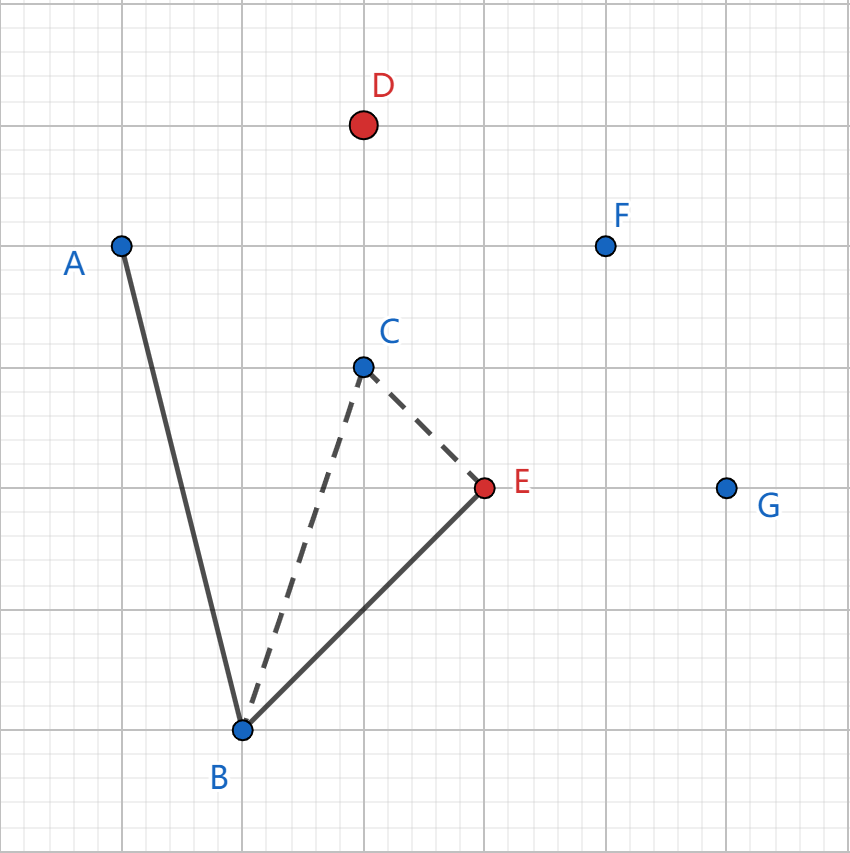
\(F\) 入栈时，发现其在栈顶的直线 \(CE\) 右侧，弹出栈顶 \(E\)；\(F\) 在栈顶的直线 \(BC\) 左侧，可以入栈：

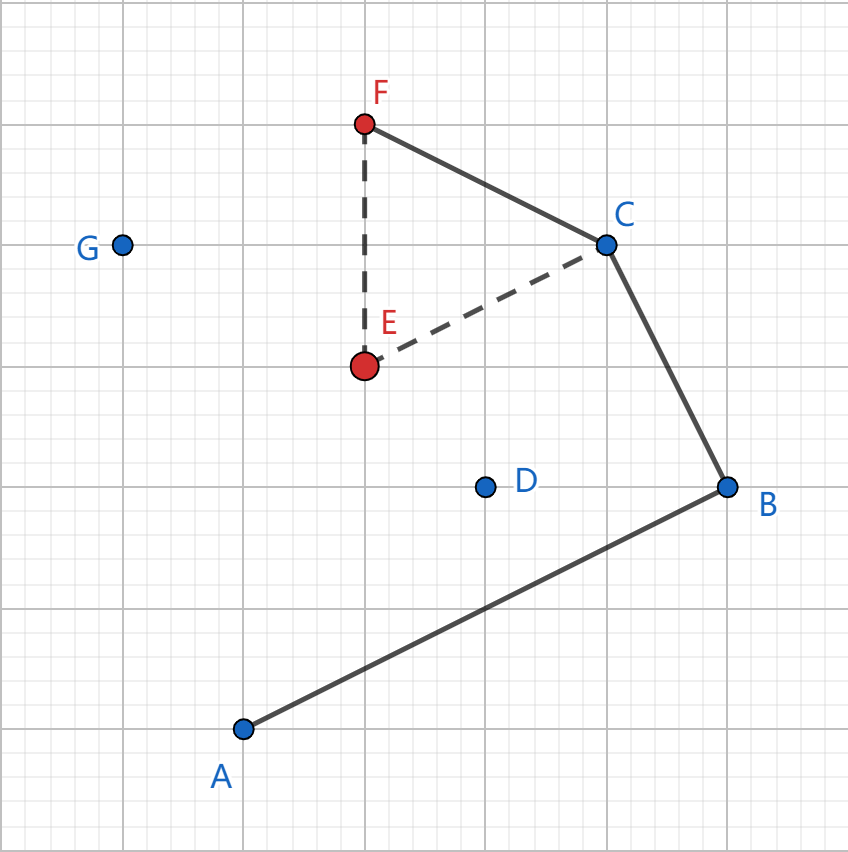
以此类推完成凸包。

复杂度为 \(\mathcal{O}(n\log n)\)。

但是求极坐标太烦，需要一个更加便捷的方法：

Andrew算法

两种算法的区别仅在排序方式不同，Andrew算法按照 \(x\) 和 \(y\) 坐标双关键字升序排序。剩下的操作同上。

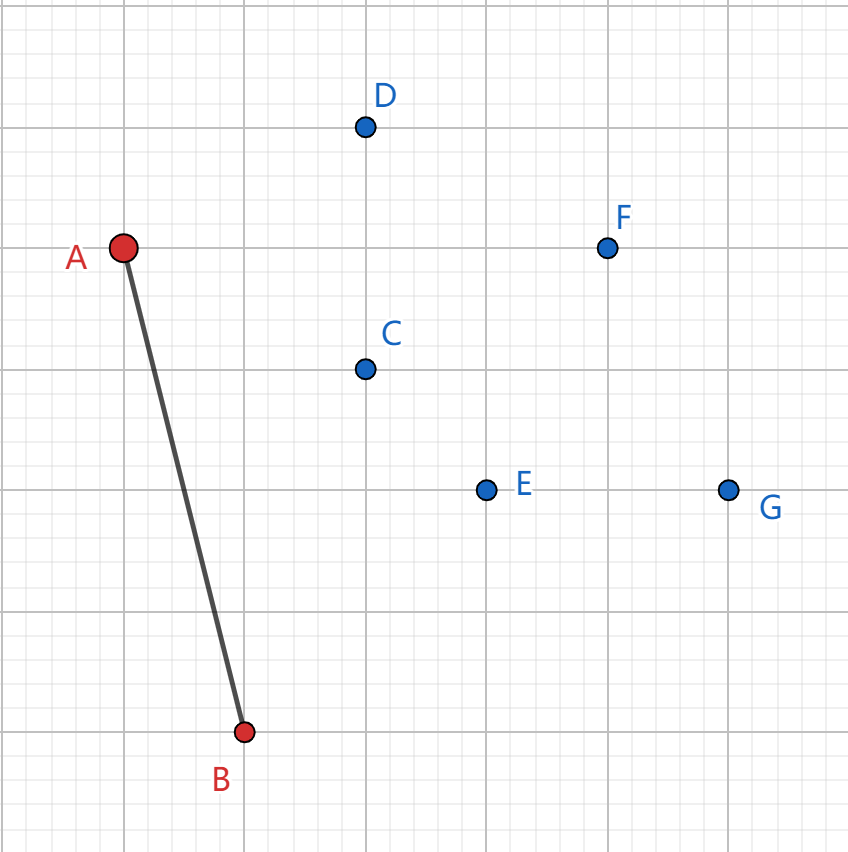
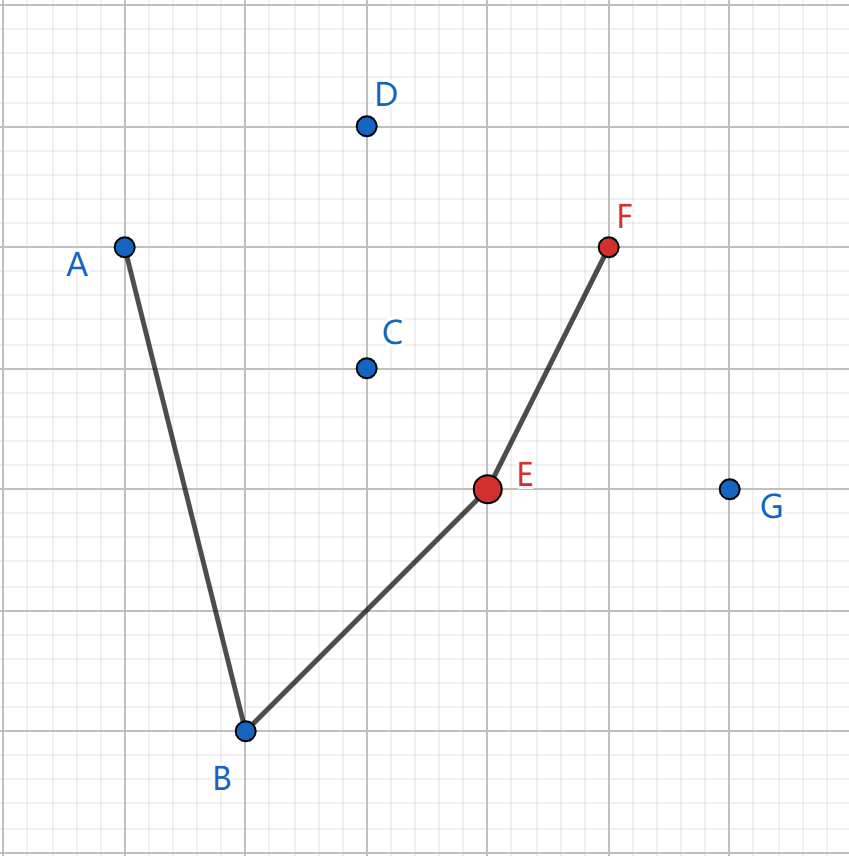
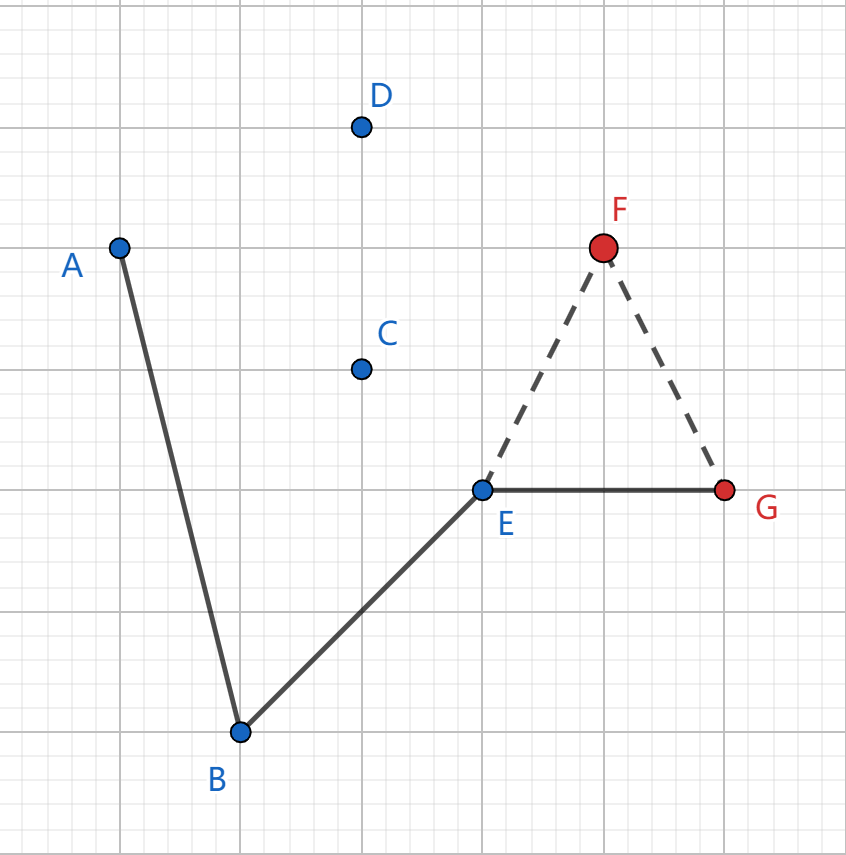
此时我们发现结束之后并没有完成整个凸包，只形成了一个下凸壳，所以，我们只需要从 \(G\sim A\) 再做一次就能得到一个完整的凸包。

例题

例 1：P2742 [USACO5.1]圈奶牛Fencing the Cows /【模板】二维凸包

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define maxn 100005
using namespace std;
int n,s[maxn],top=0; double ans=0.0;
struct point{double x,y; bool operator<(const point c)const{return x==c.x?y<c.y:x<c.x;}}a[maxn];
double dis(point xx,point yy){return sqrt(1.0*(xx.x-yy.x)*(xx.x-yy.x)+(xx.y-yy.y)*(xx.y-yy.y));}
double cross(point xx,point yy,point zz){return 1.0*(yy.x-xx.x)*(zz.y-yy.y)-(yy.y-xx.y)*(zz.x-yy.x);}
int main(){
    scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%lf%lf",&a[i].x,&a[i].y); sort(a+1,a+1+n);
    if(n<=2){printf("%.2lf",dis(a[1],a[2])); return 0;} s[++top]=1; s[++top]=2;
    for(int i=3;i<=n;i++){while(top>=2&&cross(a[s[top-1]],a[s[top]],a[i])<=0) top--; s[++top]=i;}
    for(int i=1;i<top;i++) ans+=dis(a[s[i]],a[s[i+1]]); top=0; s[++top]=n; s[++top]=n-1;
    for(int i=n-2;i>=1;i--){while(top>=2&&cross(a[s[top-1]],a[s[top]],a[i])<=0) top--; s[++top]=i;}
    for(int i=1;i<top;i++) ans+=dis(a[s[i]],a[s[i+1]]); printf("%.2lf",ans);
    return 0;
}