扫描线
顾名思义,扫描线就是二维平面内的一根不断扫描的线,能够帮助我们处理面积、周长等问题。
以矩形的面积并为例:假设平面上有 \(n\) 个矩形,求他们的面积并。如下图:
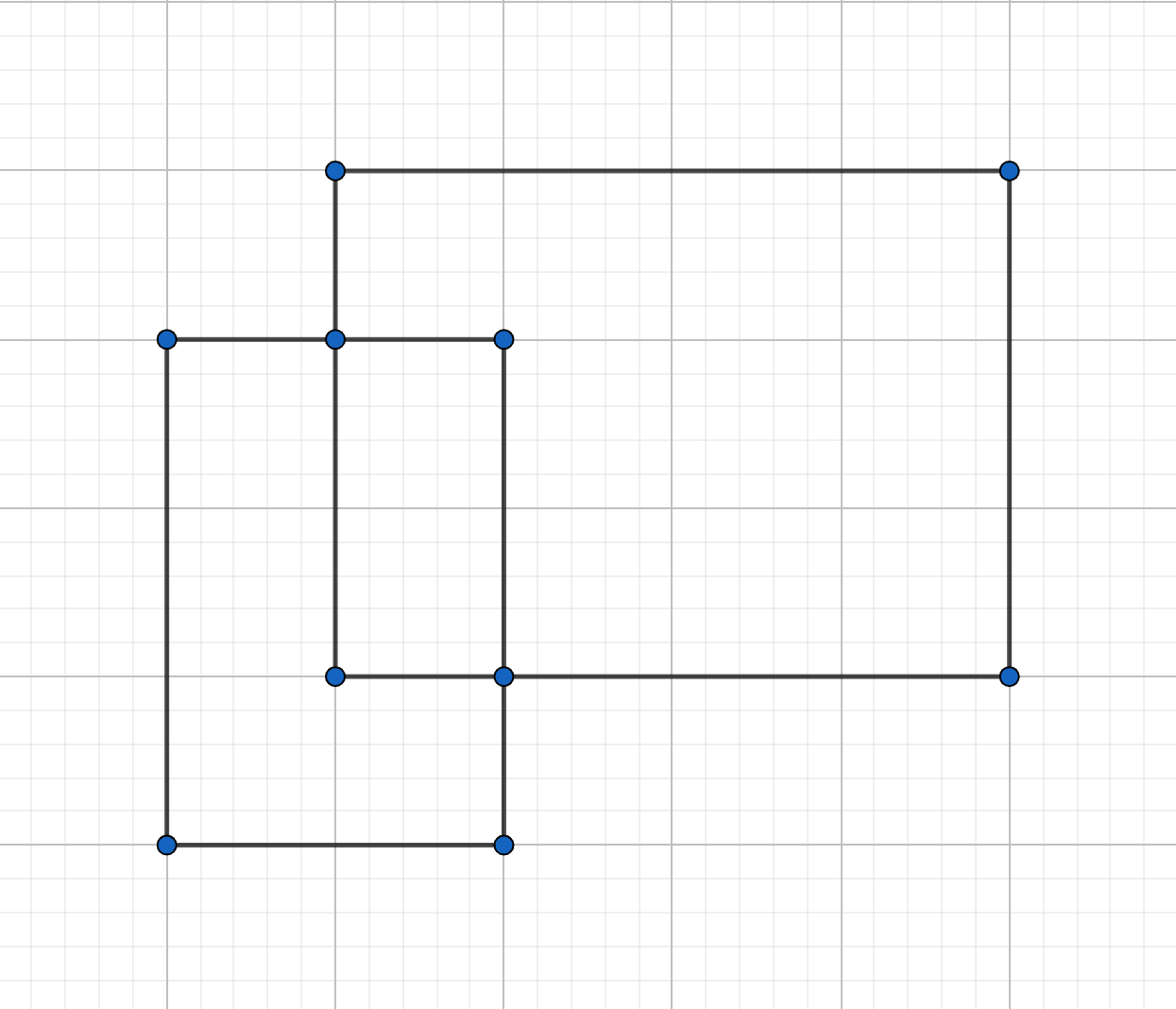
想象有一根直线 \(y=s\) 从 \(s=-\infty\) 时向上运动,触碰矩形边界时记录下来,得到 \(a,b,c,d\) 四条直线,如下图:

那么,依据这几条直线,我们将矩形的面积并划分为了几个小矩形的面积和:

结果就是矩形的面积之和。
下面我们思考如何处理,发现扫描线扫到矩形的下边界时,这条边会被加入新矩形;而扫到上边界时,会被移出新矩形,故根据上下底边赋值:
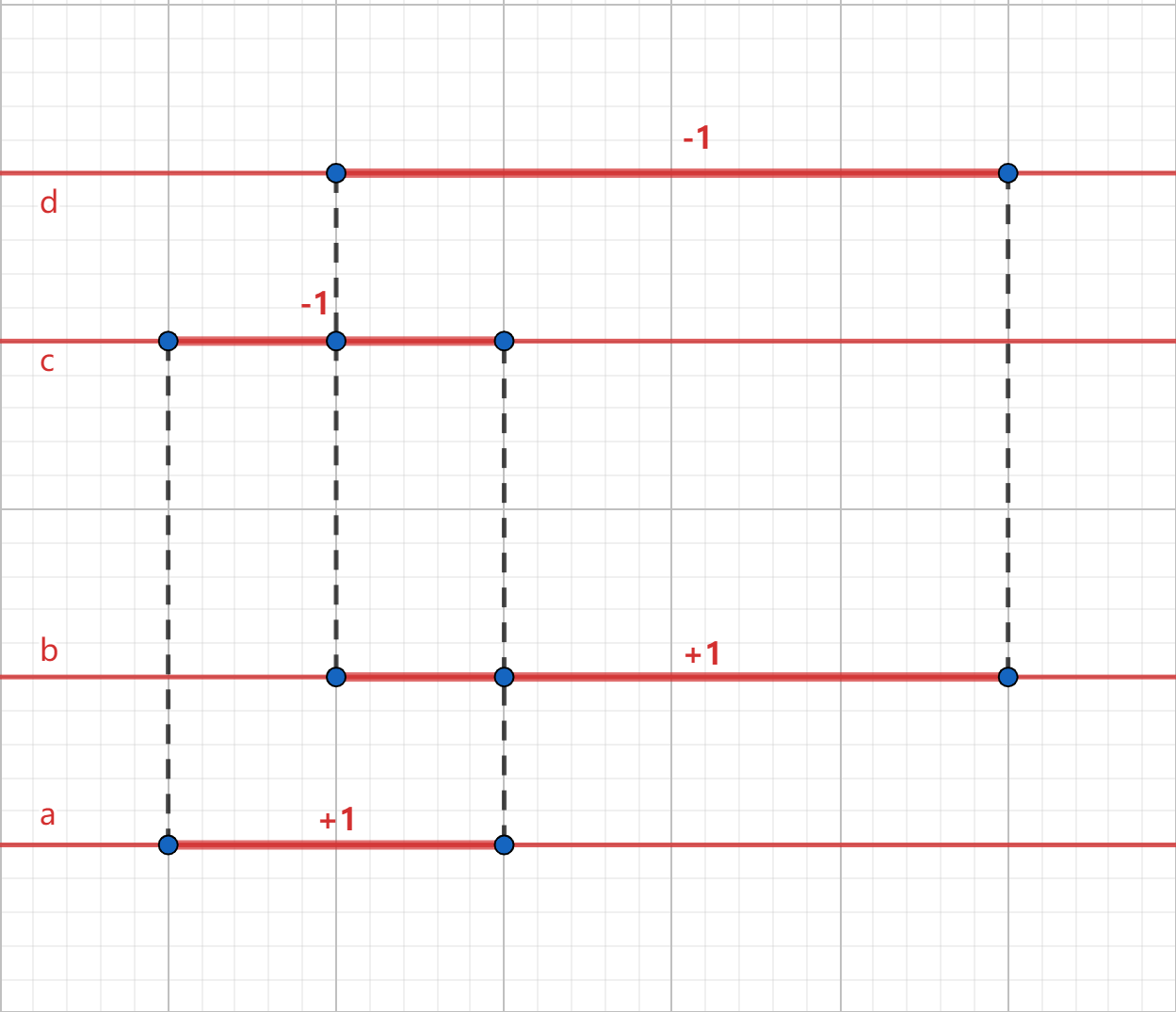
扫描线从下往上扫,碰到边就对应赋值,统计值大于 \(0\) 的长度,乘上到下一个位置的高度,即为小矩形的面积。
下图表现了扫描线扫到每个边界时的值(最上面应均为 \(0\),打错了):

区间加、区间查询,用线段树维护即可。记得离散化。
#include<iostream>
#include<cstdio>
#include<algorithm>
#define maxn 100005
#define ll long long
using namespace std;
int x1,x2,yy1,y2,n,cnt,in[maxn*2]; ll ans=0LL; struct node{int l,r,sum; ll len;}a[maxn*12];
struct rec{int x1,x2,y,plus; bool operator<(const rec c)&{return y<c.y;}}r[maxn*2];
void pushup(int p){a[p].len=a[p].sum?in[a[p].r+1]-in[a[p].l]:a[p*2].len+a[p*2+1].len;}
void build(int p,int l,int r)
{a[p].l=l; a[p].r=r; if(l==r) return; build(p*2,l,(l+r)/2); build(p*2+1,(l+r)/2+1,r);}
void add(int p,int l,int rr,int pl){
if(l<=a[p].l&&rr>=a[p].r){a[p].sum+=pl; pushup(p); return;}
if(l<=a[p*2].r) add(p*2,l,rr,pl); if(rr>=a[p*2+1].l) add(p*2+1,l,rr,pl); pushup(p);
}
int main(){
scanf("%d",&n); for(int i=1;i<=n;i++)
{scanf("%d%d%d%d",&x1,&yy1,&x2,&y2); r[2*i-1]=(rec){x1,x2,yy1,1}; r[2*i]=(rec){x1,x2,y2,-1};}
for(int i=1;i<=n*2;i+=2){in[++cnt]=r[i].x1; in[++cnt]=r[i].x2;}
sort(in+1,in+1+cnt); cnt=unique(in+1,in+1+cnt)-in-1; build(1,1,cnt); for(int i=1;i<=n*2;i+=2){
r[i].x1=r[i+1].x1=lower_bound(in+1,in+cnt+1,r[i].x1)-in;
r[i].x2=r[i+1].x2=lower_bound(in+1,in+cnt+1,r[i].x2)-in;
} sort(r+1,r+1+n*2); for(int i=1;i<n*2;i++)
{add(1,r[i].x1,r[i].x2-1,r[i].plus); ans+=1LL*a[1].len*(r[i+1].y-r[i].y);} printf("%lld",ans);
return 0;
}


