笛卡尔树

二叉查找树

笛卡尔树

定义

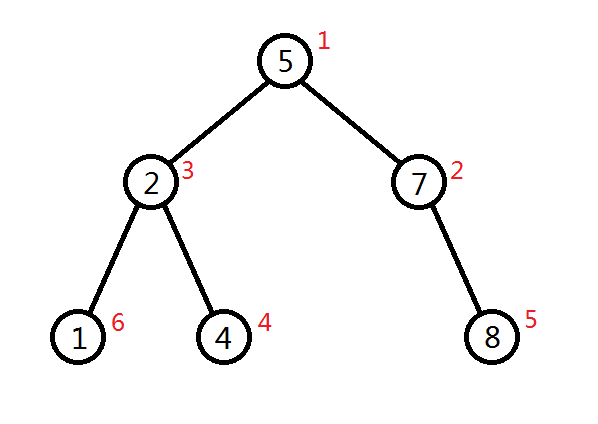
笛卡尔树是一种二叉树，每一个结点有两个键值，其中一个键值 \(k\) 符合二叉查找树的性质，另一个键值 \(w\) 符合堆的性质。如下图就是一棵笛卡尔树，其中黑色数字为符合二叉查找树的键值，红色的为符合堆（此处为小根堆）的键值：

构建

不妨假设我们需要对于数组 \(a\) 构建二叉查找树，其中每个节点的键值为 \((i,a_i)\)，即下标满足二叉查找树的性质，值满足小根堆的性质。

定义从根一直往右子树走得到的点为树的右链。

考虑按照 \(i\) 递增的顺序加点进入。因为 \(i\) 要满足二叉搜索树的性质而以 \(i\) 递增的顺序加入，所以我们新加入的点一定在右链上，需要做的就是维护这条右链。

因为 \(a_i\) 需要满足堆的性质，所以我们会将 \(i\) 插入右链中的某个位置使得其父亲的符合堆性质的键值全部小于 \(a_i\)。那么我们可能会删去若干符合堆性质的键值大于 \(a_i\) 的点，将他们放在 \(i\) 的左子树，这样既满足了二叉搜索树的性质，也满足了堆的性质。

下图是一个简单的动画，其中粉色的节点代表我们维护的右链。

在代码中，考虑到一个点只会进入和离开右链至多一次，所以可以用一个栈来维护右链，复杂度在 \(\mathcal{O}(n)\) 级别。

例题

例 1：P5854 【模板】笛卡尔树

#include<iostream>
#include<cstdio>
#define maxn 10000005
#define ll long long
using namespace std;
inline int read(){
	int res=0,neg=1; char ch=getchar(); while(!isdigit(ch)){if(ch=='-') neg=-1; ch=getchar();}
	while(isdigit(ch)){res=(res<<1)+(res<<3)+ch-'0'; ch=getchar();} return res*neg;
} int n,a[maxn],s[maxn],top=0,l[maxn],r[maxn]; ll lans=0LL,rans=0LL;
int main(){
	n=read(); for(int i=1;i<=n;i++) a[i]=read();
	for(int i=1;i<=n;i++){
		int ori=top; while(top&&a[s[top]]>a[i]) top--;
		if(top<ori) l[i]=s[top+1]; if(top) r[s[top]]=i; s[++top]=i;
	}
        for(int i=1;i<=n;i++){lans^=(1LL*i*(l[i]+1)); rans^=(1LL*i*(r[i]+1));}
        printf("%lld %lld",lans,rans);
	return 0;
}

例 2：P7988 [USACO21DEC] HILO G

题意：给定长为 \(n\) 的排列 \(a\)，现在有一个数 \(x+0.5\)（\(x\in [0,n]\)）。一个人依次按照 \(a\) 的顺序猜测 \(x+0.5\) 的值，若猜的数比 \(x+0.5\) 大了得到 HI，小了得到 LO，而且他不会进行不必要的猜测，例如询问 \(3\) 得到 HI 的结果后，就不会问 \(4,5\) 等数了。求对于所有 \(x\)，询问得到的字符串中 HILO 的数量。

发现 \(i\) 和 \(a_i\) 都会影响结果串：\(i\) 是询问的顺序，\(a_i\) 之间也会相互影响。发现在询问了 \(a_i\) 之后，剩下的询问只会全部大于 \(a_i\) 或全部小于 \(a_i\)。换句话说，询问是笛卡尔树上的一条路径，所以以 \((a_i,i)\) 为键值构建笛卡尔树。

在笛卡尔树上，发现对于节点 \(p\)，若其没有左子树，左子树就是询问 \(p-0.5\) 的结果，同样若没有右子树，右子树就是没有 \(p+0.5\) 的结果。证明不难，以左子树为例，若其大于 \(p-0.5\)，那么至少是 \(p+0.5\)，就会往右子树走，矛盾；若其小于 \(p-0.5\)，那么一定会在根到 \(p\) 的某一处走另一个方向，不会到达 \(p\)，也矛盾，所以一定会是 \(p-0.5\)，右子树同理。

#include<iostream>
#include<cstdio>
#define maxn 200005
using namespace std;
int n,x,a[maxn],s[maxn],top=0,l[maxn],r[maxn],ans[maxn],res;
void dfs(int p){
	if(!l[p]) ans[p-1]=res; else{s[++top]=1; dfs(l[p]); top--;}
	if(!r[p]) ans[p]=res+(s[top]==1);
        else{s[++top]=0; res+=(s[top-1]==1); dfs(r[p]); top--; res-=(s[top]==1);}
}
int main(){
	scanf("%d",&n); for(int i=1;i<=n;i++){scanf("%d",&x); a[x]=i;}
	for(int i=1;i<=n;i++){
		int ori=top; while(top&&a[s[top]]>a[i]) top--;
		if(top<ori) l[i]=s[top+1]; if(top) r[s[top]]=i; s[++top]=i;
	} top=0; dfs(s[1]); for(int i=0;i<=n;i++) printf("%d\n",ans[i]);
	return 0;
}