平衡树 - 有旋 Treap
二叉搜索树
二叉搜索树定义为一棵满足如下性质的二叉树:对于所有节点 \(p\),若存在左子树,左子树上所有节点的点权均小于 \(p\) 的点权;若存在右子树,右子树上所有节点的点权均大于 \(p\) 的点权。如下图:
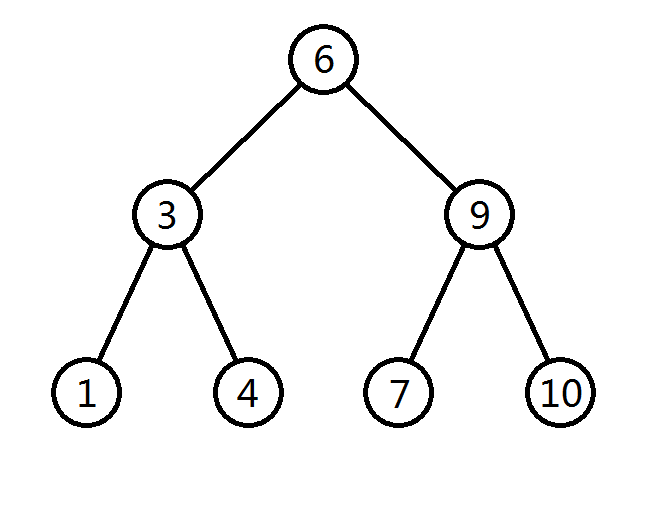
借助二叉搜索树,我们可以实现以下操作(实现方法见 Treap):
- 插入 / 删除节点;
- 查找一个数的排名 / 查找指定排名的数;
- 查找一个数的前驱 / 后继。
在这里,\(x\) 的排名定义为小于 \(x\) 的数的个数加一,\(x\) 的前驱定义为小于 \(x\) 的数中最大的一个,\(x\) 的后继定义为大于 \(x\) 的数中最小的一个。
可知,对于 \(n\) 个节点,实现上述操作的最优复杂度为 \(\mathcal{O}(\log n)\),也是随机构造一棵二叉查找树的期望高度。但是,一旦数据有序给出,二叉查找树就会退化为一条链,复杂度就会达到 \(\mathcal{O}(n)\) 级别。平衡树即优化这样的树的树高使得在复杂度控制在 \(\mathcal{O}(\log n)\) 以内的前提下实现上述操作。
有旋 Treap
简介
Treap 即 Tree + Heap,通过利用堆来控制二叉搜索树的树高。即对于一个节点,除了本身的权值外,再 随机 赋另一个关键字,通过 旋转 操作使得树高被控制。具体地,假设一棵退化为链的二叉搜索树如下图,给每一个节点 随机 赋另一个关键字如红色数字,通过一系列操作使得树满足:权值满足二叉搜索树的性质,随机的关键字符合堆的性质。这里个人习惯采用小根堆。
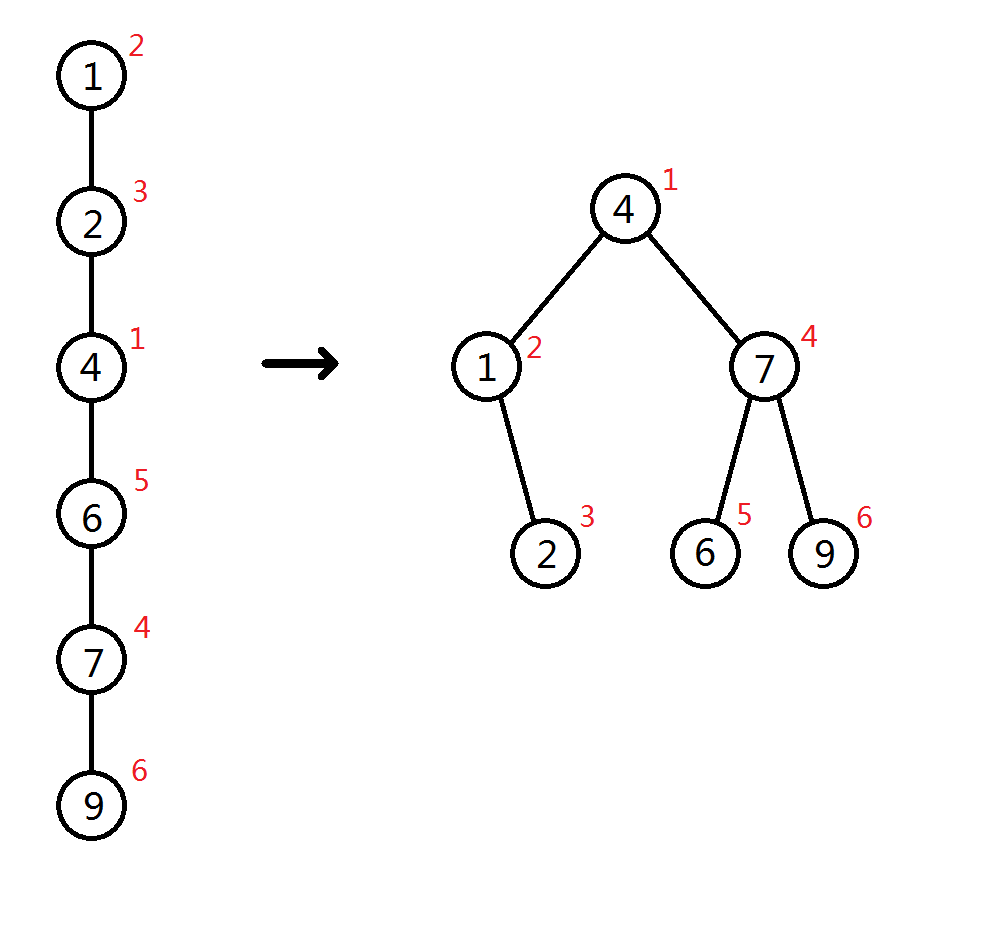
可见,随机赋的关键字可以让树高大致控制在 \(\mathcal{O}(\log n)\) 级别从而控制操作复杂度也在 \(\mathcal{O}(\log n)\) 的级别。
接下来的问题是,如何让树同时满足两个要求呢?有旋 Treap 通过 旋转 的方式解决这一个问题。旋转分为左旋(zig)和右旋(zag):
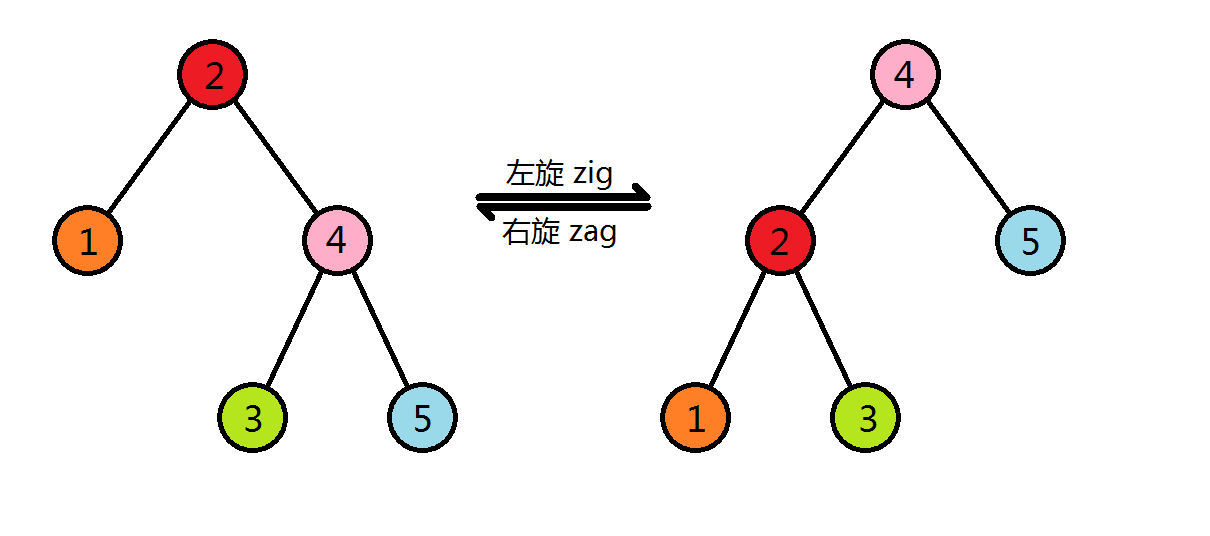
由图,旋转操作前后,二叉查找树的性质始终满足,交换了根节点和其中一个子节点的父子关系,也就意味着我们可以通过旋转调整随机的关键字使其满足堆的性质。旋转也是普通 Treap 的精髓所在。
实现
准备阶段
对于一个节点,我们需要统计:左右子树节点 \(l,r\)、权值 \(val\)、该权值的数的数量 \(cnt\)、该子树的数的数量 \(siz\) 以及随机赋的关键字 \(rnd\)。
为节约空间以及实现方便,我们采用动态开点,具体地,实现函数 \(\texttt{newnode}\) 来新建一个编号为 \(p\)、权值为 \(x\) 的节点:
int newnode(int x){
a[++cnt].val=x; a[cnt].siz=a[cnt].cnt=1;
a[cnt].rnd=rand(); return cnt;
}
以及更新节点 \(p\) 的函数 \(\texttt{pushup}\):
void pushup(int p){a[p].siz=a[a[p].l].siz+a[a[p].r].siz+a[p].cnt;}
还有旋转函数 \(\texttt{zig}\) 和 \(\texttt{zag}\)(实现方法参照上面的图):
int zag(int &p){
int res=a[p].l; a[p].l=a[res].r; a[res].r=p; p=res;
pushup(p); pushup(a[p].r);
}
int zig(int &p){
int res=a[p].r; a[p].r=a[res].l; a[res].l=p; p=res;
pushup(p); pushup(a[p].l);
}
接下来我们依次实现上述操作。
加入数
对于加入一个数 \(x\),我们将 \(x\) 与根节点的权值比较:
- 若 \(x\) 小于根节点的权值,在左子树递归;
- 若 \(x\) 大于根节点的权值,同理,在右子树递归;
- 若 \(x\) 等于根节点的权值,直接将统计数个数的 \(cnt\) 加一即可;
- 若某节点为空,新建节点,随机赋值并相应旋转维护 Treap。
void insert(int &p,int x){
if(!p){p=newnode(x); return;}
else if(a[p].val==x) a[p].cnt++;
else if(x<a[p].val){insert(a[p].l,x); if(a[p].rnd>a[a[p].l].rnd) zag(p);}
else if(x>a[p].val){insert(a[p].r,x); if(a[p].rnd>a[a[p].r].rnd) zig(p);}
pushup(p);
}
删除数
对于删除一个数 \(x\),同样将 \(x\) 与根节点的权值比较:
- 若 \(x\) 小于根节点的权值,在左子树递归;
- 若 \(x\) 大于根节点的权值,同理,在右子树递归;
- 若 \(x\) 等于根节点的权值,直接将统计数个数的 \(cnt\) 减一即可。若此时 \(cnt\) 等于 \(0\),即删完了,那么:若该节点为叶子节点,则直接删除;若该节点只有一棵子树,则将这棵子树顶替上来;否则该节点有两棵子树,将根的随机关键字较小的一棵旋转上来以维护堆的性质,之后递归直到出现前两种情况。
void erase(int &p,int x){
if(a[p].val==x){
if(a[p].cnt>1){a[p].cnt--; pushup(p); return;} // 数有多个直接删掉一个即可
if(!a[p].l) p=a[p].r; else if(!a[p].r) p=a[p].l; // 若只有一个且只有一棵子树,则让那棵顶替上来(顺便也能处理是叶子的情况)
else if(a[a[p].l].rnd>a[a[p].r].rnd){zig(p); erase(a[p].l,x);} else{zag(p); erase(a[p].r,x);} // 否则将一棵子树旋上来顶替,将删除的节点旋下去递归删掉
}else if(x>a[p].val) erase(a[p].r,x); else if(x<a[p].val) erase(a[p].l,x); pushup(p);
}
查数的排名
对于查找 \(x\) 的排名,同样将 \(x\) 与根节点的权值比较:
- 若 \(x\) 小于根节点的权值,\(x\) 的排名即 \(x\) 在左子树的排名;
- 若 \(x\) 大于根节点的权值,\(x\) 的排名即 \(x\) 在右子树的排名加上左子树的大小和根的大小(因为左子树和根的数都小于 \(x\));
- 若 \(x\) 等于根节点的权值,\(x\) 的排名即左子树的大小。
int getrank(int p,int x){
if(!p) return 1; if(x==a[p].val) return a[a[p].l].siz+1;
if(x>a[p].val) return a[a[p].l].siz+a[p].cnt+getrank(a[p].r,x);
return getrank(a[p].l,x);
}
查指定排名的数
对于查找排名为 \(x\) 的数,类似查数的排名,同样将 \(x\) 与根节点的权值比较。
int getval(int p,int x){
if(a[a[p].l].siz<x&&a[a[p].l].siz+a[p].cnt>=x) return a[p].val; // 排名大于左子树大小且小于等于左子树加根的大小的数就是根的权值
if(x<=a[a[p].l].siz) return getval(a[p].l,x); // 排名小于权值的在左子树递归
return getval(a[p].r,x-a[a[p].l].siz-a[p].cnt); // 排名大于权值的在右子树递归,要去掉左子树及根的数
}
查前驱
对于查找 \(x\) 的前驱,类似于二分,同样将 \(x\) 与根节点的权值比较。
int getpre(int p,int x){
if(!p) return -inf;
if(x>a[p].val) return max(a[p].val,getpre(a[p].r,x)); // 若数大于根的权值则查询在右子树的前驱,防止这个数是右子树中最小的将结果与根取较大值
return getpre(a[p].l,x);} // 否则在左子树递归
查后继
对于查找 \(x\) 的后继,与查找前驱基本相似。
int getnex(int p,int x){
if(!p) return inf;
if(x<a[p].val) return min(a[p].val,getnex(a[p].l,x));
return getnex(a[p].r,x);
}
例题
例 1:P3369 【模板】普通平衡树
解释看上面,以下是压行了的代码:
#include<iostream>
#include<cstdio>
#include<ctime>
#include<cstdlib>
#define maxn 100005
#define inf 100000005
using namespace std;
int n,opt,xx,root,cnt=0; struct node{int l,r,val,siz,cnt,rnd;}a[maxn];
int newnode(int x){a[++cnt].val=x; a[cnt].siz=a[cnt].cnt=1; a[cnt].rnd=rand(); return cnt;}
void pushup(int p){a[p].siz=a[a[p].l].siz+a[a[p].r].siz+a[p].cnt;}
int zag(int &p){int res=a[p].l; a[p].l=a[res].r; a[res].r=p; p=res; pushup(p); pushup(a[p].r);}
int zig(int &p){int res=a[p].r; a[p].r=a[res].l; a[res].l=p; p=res; pushup(p); pushup(a[p].l);}
void insert(int &p,int x){
if(!p){p=newnode(x); return;}else if(a[p].val==x) a[p].cnt++;
else if(x<a[p].val){insert(a[p].l,x); if(a[p].rnd>a[a[p].l].rnd) zag(p);}
else if(x>a[p].val){insert(a[p].r,x); if(a[p].rnd>a[a[p].r].rnd) zig(p);} pushup(p);
}
void erase(int &p,int x){
if(a[p].val==x){
if(a[p].cnt>1){a[p].cnt--; pushup(p); return;} if(!a[p].l) p=a[p].r; else if(!a[p].r) p=a[p].l;
else if(a[a[p].l].rnd>a[a[p].r].rnd){zig(p); erase(a[p].l,x);} else{zag(p); erase(a[p].r,x);}
}else if(x>a[p].val) erase(a[p].r,x); else if(x<a[p].val) erase(a[p].l,x); pushup(p);
}
int getrank(int p,int x){
if(!p) return 1; if(x==a[p].val) return a[a[p].l].siz+1;
if(x>a[p].val) return a[a[p].l].siz+a[p].cnt+getrank(a[p].r,x); return getrank(a[p].l,x);
}
int getval(int p,int x){
if(a[a[p].l].siz<x&&a[a[p].l].siz+a[p].cnt>=x) return a[p].val;
if(x<=a[a[p].l].siz) return getval(a[p].l,x); return getval(a[p].r,x-a[a[p].l].siz-a[p].cnt);
}
int getpre(int p,int x)
{if(!p) return -inf; if(x>a[p].val) return max(a[p].val,getpre(a[p].r,x)); return getpre(a[p].l,x);}
int getnex(int p,int x)
{if(!p) return inf; if(x<a[p].val) return min(a[p].val,getnex(a[p].l,x)); return getnex(a[p].r,x);}
int main(){
srand(time(0)); scanf("%d",&n); while(n--){
scanf("%d%d",&opt,&xx); switch(opt){
case 1: insert(root,xx); break; case 2: erase(root,xx); break;
case 3: printf("%d\n",getrank(root,xx)); break; case 4: printf("%d\n",getval(root,xx)); break;
case 5: printf("%d\n",getpre(root,xx)); break; case 6: printf("%d\n",getnex(root,xx)); break;
}
} return 0;
}
例 2:P6136 【模板】普通平衡树(数据加强版)
加了个强制在线。
#include<iostream>
#include<cstdio>
#include<ctime>
#include<cstdlib>
#define int long long
#define maxn 10000005
#define inf 9220000000000000000
using namespace std;
int n,m,opt,xx,root,cnt=0,las=0,ans=0; struct node{int l,r,val,siz,cnt,rnd;}a[maxn];
int newnode(int x){a[++cnt].val=x; a[cnt].siz=a[cnt].cnt=1; a[cnt].rnd=rand(); return cnt;}
void pushup(int p){a[p].siz=a[a[p].l].siz+a[a[p].r].siz+a[p].cnt;}
void zag(int &p){int res=a[p].l; a[p].l=a[res].r; a[res].r=p; p=res; pushup(p); pushup(a[p].r);}
void zig(int &p){int res=a[p].r; a[p].r=a[res].l; a[res].l=p; p=res; pushup(p); pushup(a[p].l);}
void insert(int &p,int x){
if(!p){p=newnode(x); return;}else if(a[p].val==x) a[p].cnt++;
else if(x<a[p].val){insert(a[p].l,x); if(a[p].rnd>a[a[p].l].rnd) zag(p);}
else if(x>a[p].val){insert(a[p].r,x); if(a[p].rnd>a[a[p].r].rnd) zig(p);} pushup(p);
}
void erase(int &p,int x){
if(a[p].val==x){
if(a[p].cnt>1){a[p].cnt--; pushup(p); return;} if(!a[p].l) p=a[p].r; else if(!a[p].r) p=a[p].l;
else if(a[a[p].l].rnd>a[a[p].r].rnd){zig(p); erase(a[p].l,x);} else{zag(p); erase(a[p].r,x);}
}else if(x>a[p].val) erase(a[p].r,x); else if(x<a[p].val) erase(a[p].l,x); pushup(p);
}
int getrank(int p,int x){
if(!p) return 1; if(x==a[p].val) return a[a[p].l].siz+1;
if(x>a[p].val) return a[a[p].l].siz+a[p].cnt+getrank(a[p].r,x); return getrank(a[p].l,x);
}
int getval(int p,int x){
if(a[a[p].l].siz<x&&a[a[p].l].siz+a[p].cnt>=x) return a[p].val;
if(x<=a[a[p].l].siz) return getval(a[p].l,x); return getval(a[p].r,x-a[a[p].l].siz-a[p].cnt);
}
int getpre(int p,int x)
{if(!p) return -inf; if(x>a[p].val) return max(a[p].val,getpre(a[p].r,x)); return getpre(a[p].l,x);}
int getnex(int p,int x)
{if(!p) return inf; if(x<a[p].val) return min(a[p].val,getnex(a[p].l,x)); return getnex(a[p].r,x);}
signed main(){
srand(time(0)); scanf("%lld%lld",&n,&m); while(n--){scanf("%lld",&xx); insert(root,xx);} while(m--){
scanf("%lld%lld",&opt,&xx); xx^=las; switch(opt){
case 1: insert(root,xx); break; case 2: erase(root,xx); break;
case 3: ans^=(las=getrank(root,xx)); break; case 4: ans^=(las=getval(root,xx)); break;
case 5: ans^=(las=getpre(root,xx)); break; case 6: ans^=(las=getnex(root,xx)); break;
}
} printf("%lld",ans); return 0;
}
例 3:P1801 黑匣子
只有插入和查指定排名的数的操作。
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<ctime>
#define maxn 200005
using namespace std;
int n,m,pos=0,p=1,in[maxn],root,cnt,xx; struct node{int l,r,cnt,siz,val,rnd;}a[maxn];
void pushup(int p){a[p].siz=a[a[p].l].siz+a[a[p].r].siz+a[p].cnt;}
int newnode(int x){a[++cnt].val=x; a[cnt].siz=a[cnt].cnt=1; a[cnt].rnd=rand(); return cnt;}
void zag(int &p){int res=a[p].l; a[p].l=a[res].r; a[res].r=p; p=res; pushup(p); pushup(a[p].r);}
void zig(int &p){int res=a[p].r; a[p].r=a[res].l; a[res].l=p; p=res; pushup(p); pushup(a[p].l);}
void insert(int &p,int x){
if(!p){p=newnode(x); return;} if(a[p].val==x) a[p].cnt++;
else if(x<a[p].val){insert(a[p].l,x); if(a[a[p].l].rnd<a[p].rnd) zag(p);}
else if(x>a[p].val){insert(a[p].r,x); if(a[a[p].r].rnd<a[p].rnd) zig(p);} pushup(p);
}
int getval(int p,int x){
if(a[a[p].l].siz<x&&a[a[p].l].siz+a[p].cnt>=x) return a[p].val;
if(a[a[p].l].siz>=x) return getval(a[p].l,x); return getval(a[p].r,x-(a[a[p].l].siz+a[p].cnt));
}
int main(){
srand(time(0)); scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&in[i]);
while(m--){scanf("%d",&xx);
while(p<=xx) insert(root,in[p++]); printf("%d\n",getval(root,++pos));}
return 0;
}

