连通性与 Tarjan
强连通分量
定义
对于一张有向图 \(G = (V,E)\),\(\forall u,v\in V\),若存在一条由 \(u\) 向 \(v\) 的有向路径,称 \(u\) 可达 \(v\)(无向图的无向边可看作是两条有向边)。
若一张图 \(G\) 的节点间两两可达,则称图 \(G\) 是强连通的。
若一张有向图 \(G\) 满足将其所有边变成无向边后可以得到一张连通图则称图 \(G\) 是弱连通的。
一张图 \(G\) 的极大连通子图称为 \(G\) 的强连通分量(SCC),同理定义弱连通分量。
如下左图,有两个强连通分量 \(\{1,2\}\) 及 \(\{3\}\)。下右图中 \(\{1,2,3\}\) 间弱连通。

DFS 生成树

由一个节点(如上图 \(1\) 号节点)开始 \(\operatorname{DFS}\),根据遍历到的边得到一棵 \(\operatorname{DFS}\) 生成树。
在 \(\operatorname{DFS}\) 生成树中,边分为 \(4\) 种:
- 树边(上图中黑色的边):\(\operatorname{DFS}\) 时搜到一个未搜过的点时形成树边;
- 返祖边/回边(上图中粉色的边):指向祖先的边;
- 横叉边(上图中蓝色的边):指向非祖先和非儿子节点的边;
- 前向边(上图中绿色的边):指向儿子的边。
考虑四种边与强连通分量的联系,我们发现:对于一个强连通分量中被 \(\operatorname{DFS}\) 到的第一个节点 \(u\),强连通分量中的其他点一定在其子树内,这个强连通分量称为以 \(u\) 为根的。
Tarjan 算法求解强连通分量
\(\operatorname{Tarjan}\) 算法求解强连通分量的过程可用一次 \(\operatorname{DFS}\) 实现。
我们需要维护两个数组 \(dfn[\ ]\) 与 \(low[\ ]\),其中 \(dfn\) 数组存 \(\operatorname{DFN}\) 序(即 \(\operatorname{DFS}\) 遍历的顺序),\(low\) 数组存节点能到达的节点中 \(dfn\) 序的最小值。
注意从根向下的任意一条路径,节点的 \(\bold{dfn}\) 递增,\(\bold{low}\) 不降。
发现当 \(\operatorname{DFS}\) 时若遇见 \(dfn_u = low_u\) 的情况,那么说明我们找到了一个以 \(u\) 为根的强连通分量,集合 \(\{v | low_v = low_u\}\) 中的点就是该强连通分量。因为该强连通分量所有点之间两两可达,所以所有点的 \(low\) 都指向 \(dfn\) 最小的点,即第一个 \(\operatorname{DFS}\) 到的节点。
接下来考虑怎么维护 \(dfn\) 和 \(low\)。
\(\operatorname{DFS}\) 的过程中依次编号 \(dfn\)。
而 \(low\) 的维护则需要以下 \(\operatorname{DFS}\) 的步骤:当遍历到节点 \(u\) 时,将其加入一个栈 \(s\) 中,遍历其子节点 \(v\):
- 若 \(v\) 未被访问(可用 \(dfn_v = 0\) 来判断):则搜索,在回溯时更新 \(low_u = \min(low_u,low_v)\),因为 \(u\) 可达 \(v\);
- 若 \(v\) 被访问过且在栈中,这意味着我们搜到了一条返祖边,直接更新 \(low_u = \min(low_u,low_v)\) 即可;
- 若 \(v\) 被访问过且不在栈中,这意味着我们搜到了一条横叉边或前向边,直接跳过。注意横叉边也可以直接跳过的原因是,因为指向的点不在栈中,所以他所在的联通块能到达的深度最小的点的深度一定大于横叉边两端点的 LCA,否则指向的点不应该出栈。
这样我们就能判断原图中强连通分量的情况了。
例题
例 1:P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G
题面:给定一张有向图。求满足所有点都可达的点的个数。
显然,若图中有且仅有一个出度为 \(0\) 的强连通分量,则这个强连通分量中的所有点都符合要求,否则不存在这样的点。
#include<iostream>
#include<cstdio>
#define maxn 10005
#define maxm 50004
using namespace std;
int n,m,u,v,tot=0,ans=0; int s[maxn],top=0,low[maxn],dfn[maxn],dfncnt=0,typ[maxn],num=0,siz[maxn],outde[maxn];
struct node{int to,nex;}a[maxm]; int head[maxn],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
void dfs(int p){
dfn[p]=low[p]=++dfncnt; s[++top]=p;
for(int i=head[p];i;i=a[i].nex)
if(!dfn[a[i].to]){dfs(a[i].to); low[p]=min(low[p],low[a[i].to]);}
else if(!typ[a[i].to]) low[p]=min(low[p],low[a[i].to]);
if(low[p]==dfn[p]){num++; while(s[top+1]!=p){siz[num]++; typ[s[top--]]=num;}}
}
int main(){
scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){scanf("%d%d",&u,&v); add(u,v);}
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);
for(int i=1;i<=n;i++) for(int j=head[i];j;j=a[j].nex) if(typ[i]!=typ[a[j].to]) outde[typ[i]]++;
for(int i=1;i<=num;i++) if(!outde[i]){tot++; ans=siz[i];} printf("%d",tot==1?ans:0);
return 0;
}
例 2:P1407 [国家集训队]稳定婚姻
题面:有 \(n\) 对情侣 \((g_i,b_i)\),其中存在一些初恋关系 \((g_i,b_j)(i\neq j)\)。当 \((g_i,b_i)\) 这段关系被打破时,\(b_i\) 就会和初恋 \(g_j\) 建立情侣关系,进而 \(b_j\) 又会和初恋 \(g_k\) 建立关系……若最后 \(n\) 对人仍然组成了 \(n\) 对情侣关系,则称 \((g_i,b_i)\) 关系是不安全的,否则是安全的。给定这些关系,求每对关系是否安全。
若关系 \((g_i,b_i)\) 被打破会引发一系列新关系建立,所以我们不妨连边 \(g_i\rightarrow b_i,b_i\rightarrow g_j,g_j\rightarrow b_j,\cdots\)。如果最后成环了,说明关系不稳定。所以只要建边后缩点,若一对关系的两点在同一强连通分量内则不稳定,否则稳定。
#include<iostream>
#include<cstdio>
#include<map>
#define maxn 8005
#define maxm 20005
using namespace std;
int n,m; map<string,int> mp; string aa,bb; struct node{int to,nex;}a[maxm*2]; int head[maxn],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
int dfn[maxn],dfncnt=0,low[maxn],s[maxn],top=0,typ[maxn],num=0;
void dfs(int p){
dfn[p]=low[p]=++dfncnt; s[++top]=p;
for(int i=head[p];i;i=a[i].nex)
if(!dfn[a[i].to]){dfs(a[i].to); low[p]=min(low[p],low[a[i].to]);}
else if(!typ[a[i].to]) low[p]=min(low[p],low[a[i].to]);
if(dfn[p]==low[p]){num++; while(s[top+1]!=p) typ[s[top--]]=num;}
}
int main(){
scanf("%d",&n); for(int i=1;i<=n;i++){cin>>aa>>bb; mp[aa]=2*i-1; mp[bb]=2*i; add(2*i-1,2*i);}
scanf("%d",&m); for(int i=1;i<=m;i++){cin>>aa>>bb; add(mp[bb],mp[aa]);}
for(int i=1;i<=2*n;i++) if(!dfn[i]) dfs(i);
for(int i=1;i<=n;i++) if(typ[2*i-1]!=typ[2*i]) printf("Safe\n"); else printf("Unsafe\n");
return 0;
}
缩点
强连通分量与缩点
缩点就是将一张有向图中的强连通分量全部缩成一个个节点,使原图形成 \(\operatorname{DAG}\),就可以进行拓扑排序等操作。而每个强连通分量内部因为是两两可达的所以也不会有影响。
具体实现就是先用 \(\operatorname{Tarjan}\) 算法求出所有强连通分量,然后再编号、建边并求解即可。
例题
例 1:P3387 【模板】缩点
题面:给定一张有向图,点有非负权值,求一条路径使得经过的点的点权和最大。可以重复经过点和边,但是一个点的点权只计一次。
既然可以重复经过点,那么有环一定会走,所以一个强连通分量中经过一个点就会将所有点走一遍。因此考虑缩点,将一个强连通分量缩成一个点,新点点权即所有点的点权和,然后跑一遍拓扑排序并 \(\operatorname{DP}\) 即可。注意原图不一定弱连通。
#include<iostream>
#include<cstdio>
#include<queue>
#define maxn 10005
#define maxm 100005
using namespace std;
int n,m,u,v,ori[maxn],ord[maxn],tot=0,outde[maxn],ans=0; struct node{int to,nex;}a[maxm*3]; int head[maxn*2],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
int dfn[maxn],dfncnt=0,low[maxn],s[maxn],top=0,typ[maxn],num=0,val[maxn],f[maxn];
void dfs(int p){
dfn[p]=low[p]=++dfncnt; s[++top]=p;
for(int i=head[p];i;i=a[i].nex)
if(!dfn[a[i].to]){dfs(a[i].to); low[p]=min(low[p],low[a[i].to]);}
else if(!typ[a[i].to]) low[p]=min(low[p],low[a[i].to]);
if(low[p]==dfn[p]){num++; while(s[top+1]!=p){typ[s[top]]=num; val[num]+=ori[s[top--]];}}
}
void topo(){
queue<int> q; bool vis[maxn]; for(int i=1;i<=num;i++){vis[i]=0; if(!outde[i]){q.push(i); ord[++tot]=i;}}
while(!q.empty()){
int top=q.front(); q.pop(); for(int j=head[top+n];j;j=a[j].nex)
{outde[a[j].to-n]--; if(!outde[a[j].to-n]){q.push(a[j].to-n); ord[++tot]=a[j].to-n;}}
}
}
int main(){
scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&ori[i]);
for(int i=1;i<=m;i++){scanf("%d%d",&u,&v); add(u,v);} for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);
for(int i=1;i<=n;i++) for(int j=head[i];j;j=a[j].nex)
if(typ[a[j].to]!=typ[i]){add(typ[a[j].to]+n,typ[i]+n); outde[typ[i]]++;} topo();
for(int i=1;i<=num;i++,ans=max(ans,f[ord[i-1]])){
f[ord[i]]=max(f[ord[i]],val[ord[i]]);
for(int j=head[ord[i]+n];j;j=a[j].nex) f[a[j].to-n]=max(f[a[j].to-n],f[ord[i]]+val[a[j].to-n]);
} printf("%d",ans);
return 0;
}
例 2:P2002 消息扩散
题面:有 \(n\) 个城市,信使可以沿这些城市间的 \(m\) 条单向道路传递信息。求至少需要给多少城市信息就能让所有城市知道信息。
显然一个强连通分量内只要有一个城市知道信息就能全部知道信息,于是把他们缩成一个点。在形成的 \(\operatorname{DAG}\) 中,只要一个点的入度不为零,那么信息一定可以从其他城市传过来,所以统计入度为零的点数即可。
#include<iostream>
#include<cstdio>
#define maxn 100005
#define maxm 500005
using namespace std;
int n,m,u,v,ans=0; struct node{int to,nex;}a[maxm]; int head[maxn],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
int dfn[maxn],dfncnt=0,low[maxn],s[maxn],top=0,typ[maxn],num=0,inde[maxn];
void dfs(int p){
dfn[p]=low[p]=++dfncnt; s[++top]=p;
for(int i=head[p];i;i=a[i].nex)
if(!dfn[a[i].to]){dfs(a[i].to); low[p]=min(low[p],low[a[i].to]);}
else if(!typ[a[i].to]) low[p]=min(low[p],low[a[i].to]);
if(low[p]==dfn[p]){num++; while(s[top+1]!=p) typ[s[top--]]=num;}
}
int main(){
scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){scanf("%d%d",&u,&v); add(u,v);}
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);
for(int i=1;i<=n;i++) for(int j=head[i];j;j=a[j].nex) if(typ[a[j].to]!=typ[i]) inde[typ[a[j].to]]++;
for(int i=1;i<=num;i++) ans+=(inde[i]==0); printf("%d",ans);
return 0;
}
例 3:P2746 [USACO5.3]校园网Network of Schools (Maybe IOI 1996)
题面:给定一张 \(n\) 点 \(m\) 边的有向图,完成两个任务:第一个即例 2,第二个即求出至少添加多少有向边才能使得原图为一个强连通分量。
任务一即例 2。接下来考虑任务二:思考缩点之后的 \(\operatorname{DAG}\),要使得这张 \(\operatorname{DAG}\) 也变成一个强连通分量,必要条件是让每个点至少有 \(1\) 的入度和出度,故答案至少为入度为零和出度为零的点的较大值。同时这也是答案的充分条件,因为可以让出入度为零的点间相互连边使得原图为强连通分量。
#include<iostream>
#include<cstdio>
#define maxn 105
#define maxm 10005
using namespace std;
int n,m,v,ans1=0,ans2=0; struct node{int to,nex;}a[maxm]; int head[maxn],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
int dfn[maxn],dfncnt=0,low[maxn],s[maxn],top=0,typ[maxn],num=0,inde[maxn],outde[maxn];
void dfs(int p){
dfn[p]=low[p]=++dfncnt; s[++top]=p;
for(int i=head[p];i;i=a[i].nex)
if(!dfn[a[i].to]){dfs(a[i].to); low[p]=min(low[p],low[a[i].to]);}
else if(!typ[a[i].to]) low[p]=min(low[p],low[a[i].to]);
if(low[p]==dfn[p]){num++; while(s[top+1]!=p) typ[s[top--]]=num;}
}
int main(){
scanf("%d",&n); for(int i=1;i<=n;i++){scanf("%d",&v); while(v){add(i,v); scanf("%d",&v);}}
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);
for(int i=1;i<=n;i++) for(int j=head[i];j;j=a[j].nex)
if(typ[a[j].to]!=typ[i]){inde[typ[a[j].to]]++; outde[typ[i]]++;}
for(int i=1;i<=num;i++){ans1+=(inde[i]==0); ans2+=(outde[i]==0);}
printf("%d\n%d",ans1,num==1?0:max(ans1,ans2));
return 0;
}
例 4:P1262 间谍网络
题面:有一张 \(n\) 个点 \(m\) 条边的有向图,可以花一定的代价控制其中的一些点,当控制一个点时,其可达的所有点都会被控制。求控制所有点的最小代价,或求出不能被控制到的点中的编号最小值。
同例 2 例 3,只要控制强连通分量中的任意一个点,整个分量都会被控制。所以将原图缩点,每个点的代价就是其中的点的代价最小值。最后找入度为零的点即可。
判无解的话只要开始的 \(\operatorname{DFS}\) 时只以能控制的起点开始搜,没搜到的点就是不能被搜到的。
#include<iostream>
#include<cstdio>
#define maxn 3005
#define maxm 8005
#define maxv 200005
using namespace std;
int n,m,u,v,val[maxn],ans=0; int dfn[maxn],dfncnt=0,low[maxn],s[maxn],top=0,typ[maxn],num=0,mmin[maxn],inde[maxn];
struct node{int to,nex;}a[maxm]; int head[maxn],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
void dfs(int p){
dfn[p]=low[p]=++dfncnt; s[++top]=p;
for(int i=head[p];i;i=a[i].nex)
if(!dfn[a[i].to]){dfs(a[i].to); low[p]=min(low[p],low[a[i].to]);}
else if(!typ[a[i].to]) low[p]=min(low[p],low[a[i].to]);
if(low[p]==dfn[p]){num++; while(s[top+1]!=p){mmin[num]=min(mmin[num],val[s[top]]); typ[s[top--]]=num;}}
}
int main(){
scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) val[i]=mmin[i]=maxv;
for(int i=1;i<=m;i++){scanf("%d",&u); scanf("%d",&val[u]);}
scanf("%d",&m); for(int i=1;i<=m;i++){scanf("%d%d",&u,&v); add(u,v);}
for(int i=1;i<=n;i++) if(!dfn[i]&&val[i]!=maxv) dfs(i);
for(int i=1;i<=n;i++) if(!dfn[i]){printf("NO\n%d",i); return 0;} printf("YES\n");
for(int i=1;i<=n;i++) for(int j=head[i];j;j=a[j].nex) if(typ[a[j].to]!=typ[i]) inde[typ[a[j].to]]++;
for(int i=1;i<=num;i++) if(!inde[i]) ans+=mmin[i]; printf("%d",ans);
return 0;
}
例 5:P1073 [NOIP2009 提高组] 最优贸易
题面:给定一张 \(n\) 个点 \(m\) 条边的有向图,每个点有权值。一个人从 \(1\) 出发,到 \(n\) 停止,在路径上他会先在一个点花这个点的点权为代价购买物品,并在之后的某个点以那个点的点权为代价卖出,求他能获得利润的最大值(请注意此处的利润并非路径中点的权值的极差,且路径一定要是 \(\bold{1\rightarrow n}\) 的)。
将所有强连通分量缩成一点,维护每个新点中点的点权最大值与最小值。得到 \(\operatorname{DAG}\) 后,我们 \(\operatorname{DP}\) 求解,维护 \(minv_p\) 表示 \(p\) 点可达的点中的最小值的最小值,就有 \(f_u = \max(\max\limits_{v\in son_u}{f_v}, max_u - maxv_u)\),其中前者即为选择的两点都在子树内,后者即为第一点在 \(u\) 而后一点在子树内。
#include<iostream>
#include<cstdio>
#include<queue>
#define maxn 100005
#define maxm 500005
using namespace std;
int n,m,u,v,opt,val[maxn],f[maxn],st,fi; struct node{int to,nex;}a[maxm*4]; int head[maxn*2],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
int dfn[maxn],dfncnt=0,low[maxn],s[maxn],top=0,typ[maxn],num=0,mmax[maxn],mmin[maxn],inde[maxn],maxv[maxn];
void dfs(int p){
dfn[p]=low[p]=++dfncnt; s[++top]=p;
for(int i=head[p];i;i=a[i].nex)
if(!dfn[a[i].to]){dfs(a[i].to); low[p]=min(low[p],low[a[i].to]);}
else if(!typ[a[i].to]) low[p]=min(low[p],low[a[i].to]);
if(low[p]==dfn[p]){
mmin[++num]=105; while(s[top+1]!=p){
typ[s[top]]=num; mmax[num]=max(mmax[num],val[s[top]]); mmin[num]=min(mmin[num],val[s[top]]);
if(s[top]==1) st=num; if(s[top]==n) fi=num; top--;
}
}
}
queue<int> q; bool vis[maxn];
void findans(){
for(int i=1;i<=num;i++) maxv[i]=mmax[i]; q.push(fi);
while(!q.empty()){
int top=q.front(); q.pop(); vis[top]=1; f[top]=max(f[top],maxv[top]-mmin[top]);
for(int i=head[top+n];i;i=a[i].nex){
f[a[i].to-n]=max(f[a[i].to-n],f[top]); maxv[a[i].to-n]=max(maxv[a[i].to-n],maxv[top]);
if(!vis[a[i].to-n]) q.push(a[i].to-n);
}
} printf("%d",f[st]);
}
int main(){
scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&val[i]);
for(int i=1;i<=m;i++){scanf("%d%d%d",&u,&v,&opt); add(u,v); if(opt==2) add(v,u);}
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);
for(int i=1;i<=n;i++) for(int j=head[i];j;j=a[j].nex)
if(typ[i]!=typ[a[j].to]){inde[typ[i]]++; add(typ[a[j].to]+n,typ[i]+n);} findans();
return 0;
}
例 6:P2169 正则表达式
题面:给定一张 \(n\) 个点 \(m\) 条边的有向图,边有边权表示长度,互相可达的两点间可以不需要代价移动,求 \(1\) 到 \(n\) 的最短路径长度。
显然一个强连通分量内点两两可达,所以在一个强连通分量内移动不需要代价,故将原图缩点后跑 \(\operatorname{Dijkstra}\) 即可。
#include<iostream>
#include<cstdio>
#include<queue>
#define maxn 200005
#define maxm 1000005
#define inf 2000000005
#define pii pair<int,int>
#define m_p make_pair
#define a_f first
#define a_s second
using namespace std;
int n,m,u,v,w,st,fi; struct node{int to,nex,dis;}a[maxm*2]; int head[maxn*2],cnt=0;
void add(int from,int to,int dis){a[++cnt].to=to; a[cnt].dis=dis; a[cnt].nex=head[from]; head[from]=cnt;}
int dfn[maxn],dfncnt=0,low[maxn],s[maxn],top=0,typ[maxn],num=0;
void dfs(int p){
dfn[p]=low[p]=++dfncnt; s[++top]=p;
for(int i=head[p];i;i=a[i].nex)
if(!dfn[a[i].to]){dfs(a[i].to); low[p]=min(low[p],low[a[i].to]);}
else if(!typ[a[i].to]) low[p]=min(low[p],low[a[i].to]);
if(low[p]==dfn[p]){num++; while(s[top+1]!=p){if(s[top]==1) st=num; if(s[top]==n) fi=num; typ[s[top--]]=num;}}
}
int f[maxn]; priority_queue<pii,vector<pii>,greater<pii> > q;
void dijk(){
for(int i=1;i<=num;i++) f[i]=inf; f[st]=0; q.push(m_p(0,st));
while(!q.empty()){
pii top=q.top(); q.pop();
for(int i=head[top.a_s+n];i;i=a[i].nex) if(f[top.a_s]+a[i].dis<f[a[i].to-n])
{f[a[i].to-n]=f[top.a_s]+a[i].dis; q.push(m_p(f[a[i].to-n],a[i].to-n));}
} printf("%d",f[fi]);
}
int main(){
scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){scanf("%d%d%d",&u,&v,&w); add(u,v,w);}
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i);
for(int i=1;i<=n;i++) for(int j=head[i];j;j=a[j].nex)
if(typ[a[j].to]!=typ[i]) add(typ[i]+n,typ[a[j].to]+n,a[j].dis); dijk();
return 0;
}
例 7:P2194 HXY烧情侣
题面: 有 \(n\) 点 \(m\) 边的有向图,摧毁点 \(i\) 需要 \(w_i\) 的代价。若存在一条路径使得起点等于终点,则摧毁这条路径上的点只需要花费起点的代价。求最小代价及最小代价下的方案数(请注意原题中只对方案数取模,不对最小代价取模)。
显然不同强连通分量间不影响,一个强连通分量内最小代价即为所有点的代价最小值,方案数即最小值的个数。最小代价为和,方案数为积。
#include<iostream>
#include<cstdio>
#define maxn 100005
#define maxm 300005
#define mod 1000000007
#define inf 2000000005
#define ll long long
using namespace std;
int n,m,u,v,val[maxn]; ll ans1=0,ans2=1; struct node{int to,nex;}a[maxm]; int head[maxn],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
int dfn[maxn],dfncnt=0,low[maxn],s[maxn],top=0,typ[maxn],num=0,mmin[maxn],siz[maxn];
void dfs(int p){
dfn[p]=low[p]=++dfncnt; s[++top]=p;
for(int i=head[p];i;i=a[i].nex)
if(!dfn[a[i].to]){dfs(a[i].to); low[p]=min(low[p],low[a[i].to]);}
else if(!typ[a[i].to]) low[p]=min(low[p],low[a[i].to]);
if(low[p]==dfn[p]){mmin[++num]=inf; while(s[top+1]!=p){typ[s[top]]=num; mmin[num]=min(mmin[num],val[s[top--]]);}}
}
int main(){
scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&val[i]);
scanf("%d",&m); for(int i=1;i<=m;i++){scanf("%d%d",&u,&v); add(u,v);}
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i); for(int i=1;i<=n;i++) siz[typ[i]]+=(val[i]==mmin[typ[i]]);
for(int i=1;i<=num;i++){ans1+=mmin[i]; ans2=(ans2*siz[i])%mod;} printf("%lld %lld",ans1,ans2);
return 0;
}
例 8:P2403 [SDOI2010]所驼门王的宝藏
题面:有一个 \(r\times c\) 的网格,其中有且仅有 \(n\) 个节点有传送门,分为三种:能传送至这一行 / 这一列 / 周围 \(8\) 格 任意格子。现在可以从任意格子进入,任意格子出来,求最多能经过的传送门数。
显然暴力建图是 \(\mathcal{O}(n^2)\) 的。我们考虑优化建图:对于同一行的横向传送门,显然他们互相可达,也就是最后会在同一个强连通分量里,于是我们对每一行开一个新点,让其与横向传送门双向连通,与其它传送门单向连通。纵向传送门同理。八连通的传送门就暴力枚。然后就是缩点 DP 了。
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<map>
#include<queue>
#define maxn 500005
#define pii pair<int,int>
#define m_p make_pair
#define a_f first
#define a_s second
using namespace std;
int dx[8]={0,1,1,1,0,-1,-1,-1},dy[8]={1,1,0,-1,-1,-1,0,1};
int n,r,c,point,ans=0; struct trans{int x,y,typ;}t[maxn]; map<pii,int> mp;
bool cmp1(trans a,trans b){if(a.x!=b.x) return a.x<b.x; return a.y<b.y;}
bool cmp2(trans a,trans b){if(a.y!=b.y) return a.y<b.y; return a.x<b.x;}
struct node{int to,nex;}a[maxn*10]; int head[maxn],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
int dfn[maxn],dfncnt=0,low[maxn],s[maxn],top=0,typ[maxn],num=0,inde[maxn],siz[maxn],f[maxn]; queue<int> q;
void dfs(int p){
dfn[p]=low[p]=++dfncnt; s[++top]=p;
for(int i=head[p];i;i=a[i].nex)
if(!dfn[a[i].to]){dfs(a[i].to); low[p]=min(low[p],low[a[i].to]);}
else if(!typ[a[i].to]) low[p]=min(low[p],low[a[i].to]);
if(low[p]==dfn[p]){num++; while(s[top+1]!=p){siz[num]+=(s[top]<=n); typ[s[top--]]=num;}}
}
void topo(){
for(int i=1;i<=num;i++) if(!inde[i]) q.push(i);
while(!q.empty()){
int top=q.front(); q.pop(); f[top]+=siz[top]; ans=max(ans,f[top]);
for(int i=head[top+point];i;i=a[i].nex){
f[a[i].to-point]=max(f[a[i].to-point],f[top]); --inde[a[i].to-point];
if(!inde[a[i].to-point]) q.push(a[i].to-point);
}
}
}
int main(){
scanf("%d%d%d",&n,&r,&c); for(int i=1;i<=n;i++)
{scanf("%d%d%d",&t[i].x,&t[i].y,&t[i].typ); mp[m_p(t[i].x,t[i].y)]=++point;};
sort(t+1,t+1+n,cmp1); point++;
for(int le=1,ri=1;ri<=n;ri++)
if(t[ri].x==t[le].x){
add(point,mp[m_p(t[ri].x,t[ri].y)]); if(t[ri].typ==1) add(mp[m_p(t[ri].x,t[ri].y)],point);
}else{le=ri; point++; ri--;}
sort(t+1,t+1+n,cmp2); point++;
for(int le=1,ri=1;ri<=n;ri++)
if(t[ri].y==t[le].y){
add(point,mp[m_p(t[ri].x,t[ri].y)]); if(t[ri].typ==2) add(mp[m_p(t[ri].x,t[ri].y)],point);
}else{le=ri; point++; ri--;}
for(int i=1;i<=n;i++) if(t[i].typ==3) for(int di=0;di<8;di++) if(mp[m_p(t[i].x+dx[di],t[i].y+dy[di])])
add(mp[m_p(t[i].x,t[i].y)],mp[m_p(t[i].x+dx[di],t[i].y+dy[di])]);
for(int i=1;i<=point;i++) if(!dfn[i]) dfs(i);
for(int i=1;i<=point;i++) for(int j=head[i];j;j=a[j].nex)
if(typ[a[j].to]!=typ[i]){add(typ[a[j].to]+point,typ[i]+point); inde[typ[i]]++;}
topo(); printf("%d",ans);
return 0;
}
割点与割边
定义
对于一张连通图 \(G = (V,E)\),若删去点 \(x\) 后图不连通了,则称 \(x\) 为图 \(G\) 的一个割点(或割顶)。
类似地,对于一张连通图 \(G = (V,E)\),若删去边 \((u,v)\) 后图不连通了,则称 \((u,v)\) 为图 \(G\) 的一条割边(或桥)。
Tarjan 算法求解割点
考虑用 \(\texttt{Tarjan}\) 算法求解所有割点。
我们发现,若对于节点 \(u\),其有一个儿子 \(v\),若 \(v\) 不能够通过边不经过 \(u\) 而到达 \(u\) 之前的节点,说明 \(u\) 是一个割点,因为删去 \(u\) 后 \(v\) 及其子树无法与其他节点连通。相反,若 \(u\) 的所有儿子 \(v\) 都能不经过 \(u\) 而到达 \(u\) 之前的节点,则 \(u\) 不是割点。
所以,我们同样记录节点的 \(\texttt{DFN}\) 序,但是 \(low_u\) 数组此时表示 \(u\) 在不经过其父亲的情况下能够到达的第一个 \(\texttt{DFN}\) 序不大于父亲的点的 \(\texttt{DFN}\) 值,而非能够到达的最小 \(\texttt{DFN}\) 值(原因底下有讲到)。那么,所有存在子节点 \(v\) 满足 \(low_v\ge dfn_u\) 的节点 \(u\) 就是割点。
注意到,只有对于一个联通块的根节点,上述方法无法判断其是否是割点,因为所有点能达到的 \(\texttt{DFN}\) 序最小的点就是它,这会导致它一定会成为割点。事实并不是如此,所以要额外特判。根节点不是割点当且仅当它的子树间全部都能不经过它连通,那么我们只要记录以它往下的儿子个数,若大于 \(1\) 则它的确是个割点。
此时我们的实现方式就和求强连通分量时的 \(\texttt{Tarjan}\) 基本相同了,但是我们不需要栈 \(s\) 来统计哪些点在一个强连通分量里了,也不需要判断搜的边是否是横叉边或前向边,因为它们对答案同样有贡献。
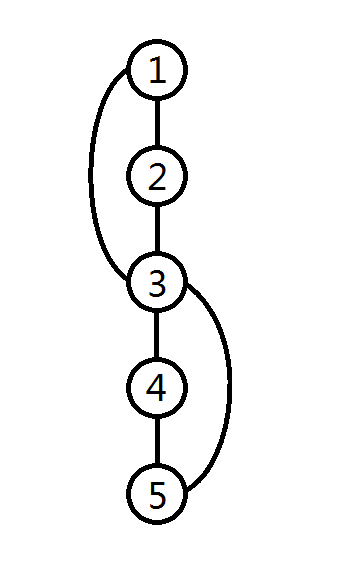
而且,返祖边、横叉边和前向边的 \(low\) 值更新要变为 low[p]=min(low[p],dfn[a[i].to]) 而非 low[p]=min(low[p],low[a[i].to]) 了。具体原因就是刚才对于 \(low\) 数组定义的改变。对于下图,假设搜的顺序为 \(1\rightarrow2\rightarrow3\rightarrow1\rightarrow4\rightarrow5\rightarrow3\),在搜到最后一个 \(3\) 时,\(low_3 = 1\),若采用 low[p]=min(low[p],low[a[i].to]) 则会将 \(low_5\) 的值更新为 \(1\),回溯到 \(4\) 时更新 \(low_4=1\),同理会更新 \(low_3 = 1\),不会找到割点。而若采用 low[p]=min(low[p],dfn[a[i].to]),\(low_5\) 的值为 \(3\),\(low_4\) 的值就会为 \(3\),就会有 \(low_4\ge dfn_3\),找到割点 \(3\)。所以,采用后一种方式,能规避节点 \(v\) 跳到 \(u\) 上方的 \(w\) 后通过 \(w\) 的返祖边跳到更上方,导致损失了 \(w\) 这一个可能的割点。
Tarjan 算法求割边
类似割点,割边的求法只需要将 \(low_v\ge dfn_u\) 改为 \(low_v > dfn_u\) 即可,且根节点的问题无需考虑。
例题
例 1:P3388 【模板】割点(割顶)
题面:输入一张图,输出所有的割点。
#include<iostream>
#include<cstdio>
#define maxn 20005
#define maxm 100005
using namespace std;
int n,m,u,v,ans; bool anss[maxn]; struct node{int to,nex;}a[maxm*2]; int head[maxn],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
int dfn[maxn],dfncnt=0,low[maxn];
void dfs(int p,int fa){
dfn[p]=low[p]=++dfncnt; int son=0; for(int i=head[p];i;i=a[i].nex) if(a[i].to!=fa){
if(!dfn[a[i].to]){
son++; dfs(a[i].to,p); low[p]=min(low[p],low[a[i].to]);
if(fa!=p&&!anss[p]&&low[a[i].to]>=dfn[p]){anss[p]=1; ans++;}
} low[p]=min(low[p],dfn[a[i].to]);
} if(fa==p&&son>1){anss[p]=1; ans++;}
}
int main(){
scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){scanf("%d%d",&u,&v); add(u,v); add(v,u);}
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i,i);
printf("%d\n",ans); for(int i=1;i<=n;i++) if(anss[i]) printf("%d ",i);
return 0;
}
/*
Hack
5 6
5 3
4 5
3 4
3 1
2 3
1 2
*/
例 2:P3469 [POI2008]BLO-Blockade
题面:给定一张 \(n\) 个点 \(m\) 条边的无向图,求出对于每个点,若删去与该点相连的所有边(不删除该点),有多少无序点对 \((x,y)\)(\(x\neq y\))满足不能从 \(x\) 到达 \(y\)。
考虑割掉与一个点 \(i\) 相连的所有边的影响:首先 \(i\) 不能到达其余点,有 \(2(n-1)\) 的贡献;然后,所有 \(i\) 的儿子 \(p\) 中,若没有边回到 \(i\) 之上,即 \(low_p\ge dfn_i\),那么这棵子树就会独立开来,若有 \(k\) 棵这样的子树,就有 \(2\sum\limits_{i=1}^k siz_i\times(n-1-siz_i) + 2(n-1)\) 的贡献。
#include<iostream>
#include<cstdio>
#define maxn 100005
#define maxm 500005
#define ll long long
using namespace std;
int n,m,u,v; ll anss[maxn]; struct node{int to,nex;}a[maxm*2]; int head[maxn],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
int dfn[maxn],dfncnt=0,low[maxn],siz[maxn];
void dfs(int p,int fa){
low[p]=dfn[p]=++dfncnt; siz[p]=1; ll sum=0LL; for(int i=head[p];i;i=a[i].nex) if(a[i].to!=fa){
if(!dfn[a[i].to]){
dfs(a[i].to,p); siz[p]+=siz[a[i].to]; low[p]=min(low[p],low[a[i].to]);
if(low[a[i].to]>=dfn[p]){anss[p]+=1LL*sum*siz[a[i].to]; sum+=siz[a[i].to];}
}else low[p]=min(low[p],dfn[a[i].to]);
} anss[p]+=1LL*sum*(n-sum-1)+1LL*(n-1);
}
int main(){
scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){scanf("%d%d",&u,&v); add(u,v); add(v,u);}
for(int i=1;i<=n;i++) if(!dfn[i]) dfs(i,i); for(int i=1;i<=n;i++) printf("%lld\n",2LL*anss[i]);
return 0;
}

