自适应辛普森法

积分

积分是微积分学与数学分析里的一个核心概念。通常分为定积分和不定积分两种。

定积分

简单地说，若函数 \(f(x)\) 在区间 \([l,r]\) 上是连续的，其图像与 \(x\) 轴围成的面积（\(x\) 轴以上为正，以下为负）称为函数 \(f(x)\) 在 \([l,r]\) 上的定积分，记作：

\[\displaystyle{\int_l^rf(x)\,\mathrm{d}x} \]

例如：\(\displaystyle{\int_{-1}^2x\,\mathrm{d}x} = \dfrac{3}{2}\)。

其严格定义是将 \([l,r]\) 区间分成 \(n\) 个等长小段 \([l,x_1],(x_1,x_2],(x_2,x_3],\cdots,(x_{n-2},x_{n-1}],(x_{n-1},r]\)（每段长 \(\Delta x = \dfrac{r-l}{n}\)），将每一段内图像与 \(x\) 轴围成的面积视为一个矩形（在段数增加时该图形会越来越趋近矩形），第 \(i\) 个矩形面积就用 \(f(l+i\Delta x)\cdot\Delta x\) 表示（这里以区间右边界为矩形的高，其实中间的任一值均可，因为矩形个数增加时这些值趋近相等），所以整个图形的面积就是：

\[\displaystyle{\int_l^rf(x)\,\mathrm{d}x}= \lim\limits_{n\to +\infty}\sum\limits_{i=1}^{n}{f(l+\frac{i(r-l)}{n})\cdot\dfrac{r-l}{n}} \]

下面是定积分的一些性质：

• \(\displaystyle{\int_l^lf(x)\,\mathrm{d}x} = 0\)；
• \(\displaystyle{\int_l^rkf(x)\,\mathrm{d}x = k\cdot\int_l^rf(x)\,\mathrm{d}x}\)（\(k\) 为常数）；
• \(\displaystyle{\int_l^r[f(x)\pm g(x)]\,\mathrm{d}x = \displaystyle{\int_l^rf(x)\,\mathrm{d}x} \pm \displaystyle{\int_l^rg(x)\,\mathrm{d}x}}\)；
• \(\displaystyle{\int_l^pf(x)\,\mathrm{d}x + \int_p^rf(x)\,\mathrm{d}x = \int_l^rf(x)\,\mathrm{d}x}\)；
• 若 \(f(x)\) 在 \([l,r]\) 上连续，则 \(\exists\varepsilon\in[l,r]\) 使得 \(\displaystyle{\int_l^rf(x)\,\mathrm{d}x} = f(\varepsilon)(b-a)\)，即积分中值定理。

不定积分

函数 \(f(x)\) 的不定积分 \(F(x)\)，满足 \(F'(x) = f(x)\)，记作：

\[\displaystyle{\int f(x)\,\mathrm{d}x} = F(x) \]

例如：\(\displaystyle{\int 2x\,\mathrm{d}x} = x^2 + C\)（\(C\) 为常数）。

下面是不定积分的一些性质：

• \(\displaystyle{\int[f(x)\pm g(x)]\,\mathrm{d}x = \int f(x)\,\mathrm{d}x \pm \int g(x)\,\mathrm{d}x}\)；
• \(\displaystyle{\int kf(x)\,\mathrm{d}x = k\cdot\int f(x)\,\mathrm{d}x}\)（\(k\) 为常数）。

下面是常见函数的不定积分（\(C\) 代表常数）：

• \(\displaystyle{\int a\,\mathrm{d}x} = ax + C\)；
• \(\displaystyle{\int x^a\,\mathrm{d}x} = \begin{cases}\dfrac{x^{a+1}}{a+1} + C&a\neq -1\\\\\ln|x|+C&a=-1\end{cases}\)；
• \(\displaystyle{\int a^x\,\mathrm{d}x} = \dfrac{a^x}{\ln a} + C\)（\(a>0\) 且 \(a\neq 1\)），
  特殊地，\(a = e\) 时得到 \(\displaystyle{\int e^x\,\mathrm{d}x} = e^x + C\)；

微积分基本定理

微积分基本定理，即牛顿 - 莱布尼茨公式，揭示了定积分与不定积分之间的关系：

若 \(f(x)\) 在 \([l,r]\) 上连续且存在不定积分 \(F(x)\)，则有：

\[\displaystyle{\int_l^rf(x)\,\mathrm{d}x} = F(b) - F(a) = F(x)|\,_a^b \]

自适应辛普森法

辛普森公式

辛普森公式即在函数 \(f(x)\) 的区间 \([l,r]\) 上找三个点 \(l,mid,r\)，用二次函数拟合这一段函数图像，用二次函数在这一段上的定积分来近似原函数 \(f(x)\) 在 \([l,r]\) 上的定积分。

公式内容为：

\[\displaystyle{\int_l^rf(x)\,\mathrm{d}x}\approx \dfrac{(r-l)(f(l)+4f(\frac{l+r}{2})+f(r))}{6} \]

推导：

对于函数 \(f(x)\)，用二次函数 \(Ax^2 + Bx + C\) 拟合（\(Ax^2 + Bx + C\) 的不定积分为 \(\dfrac{A}{3}x^3 + \dfrac{B}{2}x^2 + Cx + D\)，其中 \(D\) 为常数）。

\[\begin{aligned} \displaystyle{\int_l^rf(x)\,\mathrm{d}x}&\approx \displaystyle{\int_l^r Ax^2 + Bx + C\,\mathrm{d}x}\\ &=\dfrac{A}{3}(r^3 - l^3) + \dfrac{B}{2}(r^2 - l^2) + C(r - l)\\ &=\dfrac{r-l}{6}(2A(r^2 + lr + l^2) + 3B(l + r) + 6C)\\ &=\dfrac{r-l}{6}[(Al^2 + Bl + C) + (Ar^2 + Br + C) + (4A(\frac{l + r}{2})^2 + 4B(\frac{l + r}{2}) + 4C)]\\ &=\dfrac{(r-l)(f(l)+4f(\frac{l+r}{2})+f(r))}{6} \end{aligned} \]

即：

double simpson(double l,double r){return (r-l)*(cal(l)+cal(r)+4*cal((l+r)/2))/6;}

其中 \(\operatorname{cal}\) 计算函数值。

自适应辛普森法

而单纯地拟合整个区间会导致精度偏差很大。

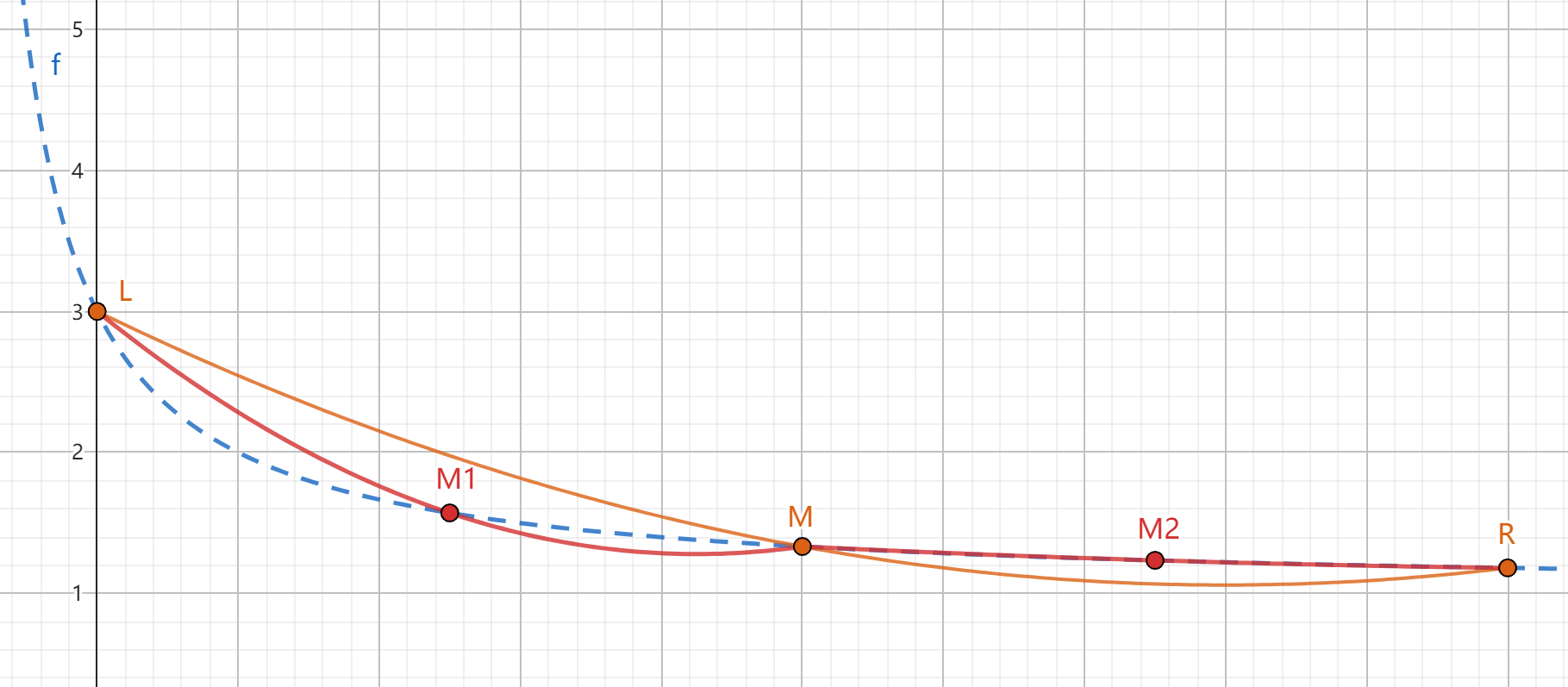
如图，蓝色虚线即为函数 \(f(x)\)，在区间 \([0,10]\) 上拟合得到橙色二次函数，在 \([0,5]\) 和 \([5,10]\) 上用同样的方式分别拟合得到红色二次函数，显然不断二分下去得到的定积分值就会越来越精确。

所以，自适应辛普森法就是利用了这样一个不断二分的过程，若二分的结果与整段的结果相差不大则不继续递归二分，就能得到整个区间的定积分值。

以洛谷的模板题为例，要求 \(\displaystyle{\int_e^f\dfrac{cx+d}{ax+b}\,\mathrm{d}x}\) 的值，代码如下：

#include<iostream>
#include<cstdio>
#define eps 1e-12
using namespace std;
double a,b,c,d,l,r;
double fabs(double xx){return xx<0?-xx:xx;}
double cal(double pos){return (c*pos+d)/(a*pos+b);}
double simpson(double l,double r){return (r-l)*(cal(l)+cal(r)+4*cal((l+r)/2))/6;}
double asr(double l,double r,double res,int step){
    if(step==0) return res; double mid=(l+r)/2,al=simpson(l,mid),ar=simpson(mid,r);
    if(fabs(al+ar-res)<=eps) return al+ar;
    return asr(l,mid,al,step-1)+asr(mid,r,ar,step-1);
}
int main(){
    scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&l,&r);
    printf("%.6lf",asr(l,r,simpson(l,r),10));
    return 0;
}

显然，板题也可以纯数学推导：

\[\begin{aligned} \displaystyle{\int\dfrac{cx+d}{ax+b}\,\mathrm{d}x}&=\displaystyle{\int(\dfrac{c}{a}+\dfrac{d-\frac{bc}{a}}{ax+b})\,\mathrm{d}x}\\ &=\displaystyle{\int\dfrac{c}{a}\,\mathrm{d}x} + \dfrac{ad-bc}{a}\displaystyle{\int\dfrac{1}{ax+b}\,\mathrm{d}x} \end{aligned} \]

所以就有：

\[\displaystyle{\int\dfrac{cx+d}{ax+b}\,\mathrm{d}x} = \dfrac{ad-bc}{a^2}\ln|ax+b| + \dfrac{c}{a}x + C \]

即：

\[\displaystyle{\int_e^f\dfrac{cx+d}{ax+b}\,\mathrm{d}x} = (\dfrac{ad-bc}{a^2}\ln|ax+b| + \dfrac{c}{a}x )|\,_e^f \]

注意特判 \(a = 0\) 的数据。