树链剖分
树链剖分
概念简介
树链剖分,即树剖,能够将树分解为若干条链,使其可组合为线性结构,再使用其他线性结构来维护原树。
树剖有多种形式,如 重链剖分、长链剖分等,常用的是重链剖分(轻重链剖分)。
重链剖分能够将树上的一条简单路径划分为不大于 \(\mathcal{O}(\log n)\) 条连续的链,且保证 DFN 序连续,以便用 线性的数据结构 如线段树与树状数组等维护路径信息。
同时,树剖也是 \(\mathcal{O}(\log n)\) 求 \(\operatorname{LCA}\) 的方法之一。
一些定义
对于一棵树,定义两点间简单路径为两点间的最短路径,即不经过重复点、重复边从一点走到另一点的路径。
定义重子节点(重儿子)为一个点的所有子节点中子树大小最大的一个,其余的为轻子节点(轻儿子)。
定义节点到其重儿子之间的边为重边,其余的为轻边。
定义将若干条连续的重边及对应的节点连接得到的链为重链,特殊地,单个节点也算重链。这样就能将这棵树剖分为若干重链。
定义将树 DFS 一遍,按照第一次到某个点的顺序将点编号,得到 DFN 序(显然不唯一)。在重链剖分中的 DFS 我们先搜重儿子所在的子树,后搜轻儿子所在的子树,这样就能够保证:所有重链和所有子树内的 DFN 序全部都是连续的。(前者因先搜重儿子的搜索方式决定,后者因 DFN 序的特性决定)
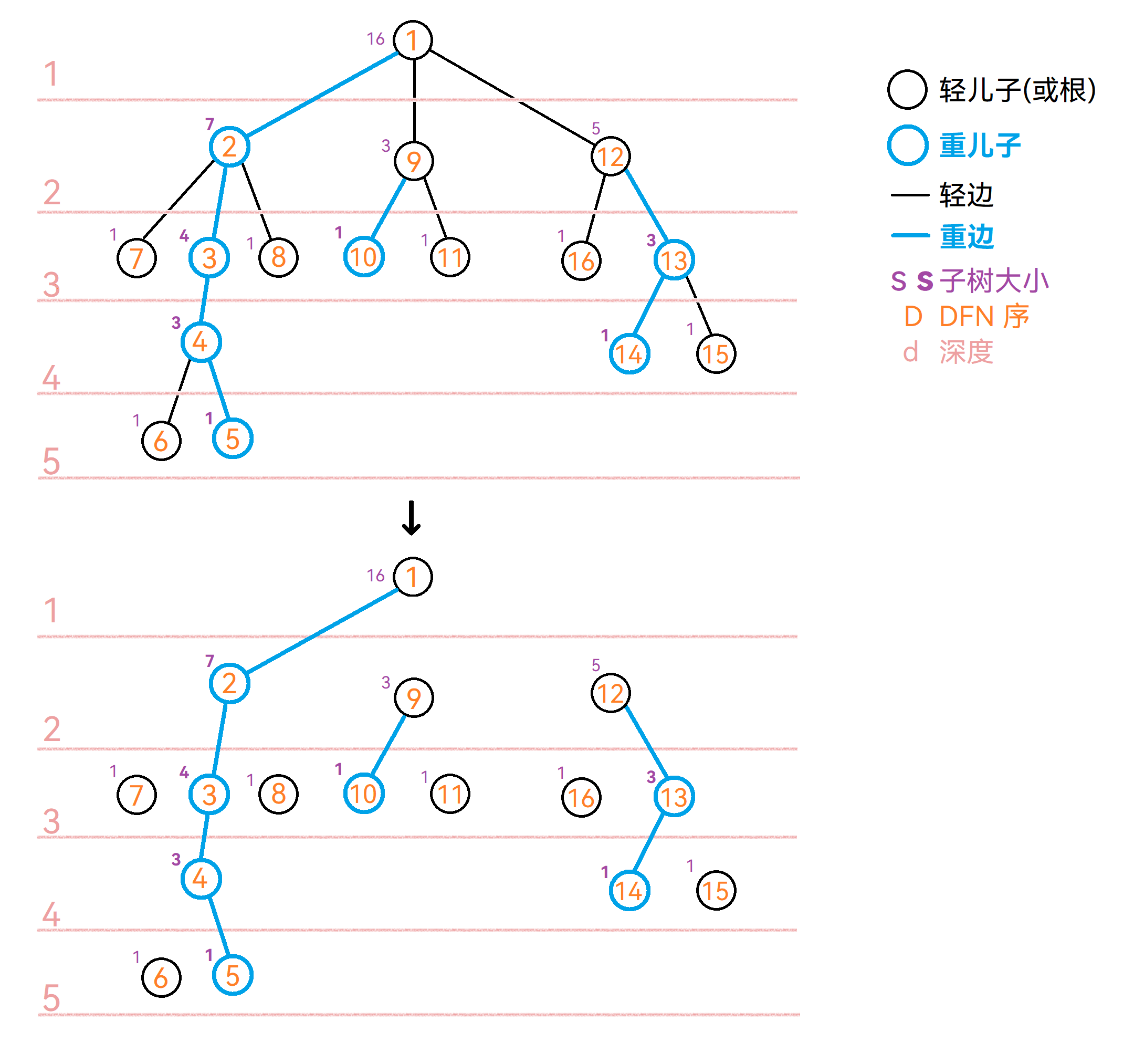
现在我们就将原树剖分为了若干重链。
结论
-
树上每个节点都 属于且只属于一条重链,重链将整棵树 完全剖分;
-
所有重链和所有子树内的 DFN 序全部 都是连续的;
-
对于任意一条路径 \(u\rightarrow v\),看作是 \(\operatorname{LCA}(u,v)\rightarrow u\) 与 \(\operatorname{LCA}(u,v)\rightarrow v\),最多走 \(\mathcal{O}(\log n)\) 次,即每条路径都可以分成 \(\mathcal{O}(\log n)\) 条重链。这是重链剖分复杂度的基础。
既然每一条链上的节点 DFN 序都是连续的,我们用 DFN 序给节点 重编号,这样任意一条路径 / 子树都能转化为区间修改 / 查询,可以用线段树 / 树状数组维护。这门只需要维护每一条链的端点(深度最小的端点)即可。
我们结合例 1 进行详细解释。
例题
例 1:P3384 【模板】轻重链剖分/树链剖分
题目大意
给定一棵有 \(n\) 个节点的树,维护以下操作:
-
从 \(x\) 到 \(y\) 之间的简单路径上所有节点的权值都加上 \(z\);
-
查询从 \(x\) 到 \(y\) 之间的简单路径上所有节点的权值和;
-
将以 \(x\) 为根的子树内的所有节点的权值都加上 \(y\);
-
查询以 \(x\) 为根的子树内的所有节点的权值和。
思路
预处理
树链剖分需要两次预处理,第一次预处理出:深度 \(\texttt{dep}\)、子树大小 \(\texttt{siz}\)、重儿子编号 \(\texttt{son}\)、父节点编号 \(\texttt{fa}\)。
第二次预处理出:所在重链的端点 \(\texttt{top}\)、DFN 序 \(\texttt{id}\)。
两次 \(\operatorname{DFS}\) 即可。复杂度显然是 \(\mathcal{O}(n)\) 的。
void dfs1(int p,int f){
dep[p]=dep[f]+1; siz[p]=1; fa[p]=f; for(int i=head[p];i;i=t[i].nex) if(t[i].to!=f)
{dfs1(t[i].to,p); siz[p]+=siz[t[i].to]; son[p]=(siz[t[i].to]>siz[son[p]]?t[i].to:son[p]);}
}
void dfs2(int p,int tp){
top[p]=tp; id[p]=++tot; sid[tot]=p; if(!son[p]) return; dfs2(son[p],tp);
for(int i=head[p];i;i=t[i].nex) if(t[i].to!=fa[p]&&t[i].to!=son[p]) dfs2(t[i].to,t[i].to);
}
操作 1、2
前两个操作都是路径上的操作,我们考虑一个类似倍增求 \(\operatorname{LCA}\) 的思想,选择 \(u,v\) 两点中所在链的端点深度较大的向上跳一条链,期间维护加法,直到两点进入同一条链即可。
void t_add(int p1,int p2,int ad){
while(top[p1]!=top[p2]){if(dep[top[p1]]<dep[top[p2]]) swap(p1,p2); add(1,id[top[p1]],id[p1],ad); p1=fa[top[p1]];}
if(dep[p1]>dep[p2]) swap(p1,p2); add(1,id[p1],id[p2],ad);
}
ll t_search(int p1,int p2){
ll res=0; while(top[p1]!=top[p2]){if(dep[top[p1]]<dep[top[p2]]) swap(p1,p2); res=(res+search(1,id[top[p1]],id[p1]))%mod; p1=fa[top[p1]];}
if(dep[p1]>dep[p2]) swap(p1,p2); res=(res+search(1,id[p1],id[p2]))%mod; return res;
}
...
if(opt==1){scanf("%d%d%d",&x,&y,&z); t_add(x,y,z);}
else if(opt==2){scanf("%d%d",&x,&y); printf("%lld\n",t_search(x,y));}
操作 3、4
后两个操作都是子树内的操作,由于编号连续,\(x\) 子树中的编号一定为 \(id_x\sim id_x + siz_x - 1\),即可维护。
if(opt==3){scanf("%d%d",&x,&y); add(1,id[x],id[x]+siz[x]-1,y);}
else if(opt==4){scanf("%d",&x); printf("%lld\n",search(1,id[x],id[x]+siz[x]-1));}
复杂度应该都是 \(\mathcal{O}(n\log^2n)\) 的。
其余的只需要线段树 / 树状数组维护即可。
代码
#include<iostream>
#include<cstdio>
#define maxn 100005
#define ll long long
using namespace std;
int n,m,root,mod,in[maxn]; int dep[maxn],siz[maxn],son[maxn],fa[maxn],top[maxn],id[maxn],sid[maxn],tot=0;
int opt,x,y,z; struct node{int to,nex;}t[maxn*2]; int head[maxn],cnt=0;
struct seg_tree{int l,r; ll sum=0,lt=0;}a[maxn*4]; void push_up(int p){a[p].sum=(a[p*2].sum+a[p*2+1].sum)%mod;}
void push_down(int p){ if(!a[p].lt) return;
a[p*2].lt=(a[p*2].lt+a[p].lt)%mod; a[p*2+1].lt=(a[p*2+1].lt+a[p].lt)%mod;
a[p*2].sum=(a[p*2].sum+a[p].lt*(a[p*2].r-a[p*2].l+1)%mod)%mod;
a[p*2+1].sum=(a[p*2+1].sum+a[p].lt*(a[p*2+1].r-a[p*2+1].l+1)%mod)%mod; a[p].lt=0;
}
void build(int p,int l,int r)
{a[p].l=l; a[p].r=r; if(l==r){a[p].sum=in[sid[l]]%mod; return;} build(p*2,l,(l+r)/2); build(p*2+1,(l+r)/2+1,r); push_up(p);}
void add(int p,int l,int r,int ad){
if(a[p].l>=l&&a[p].r<=r){a[p].lt=(a[p].lt+1LL*ad)%mod; a[p].sum=(a[p].sum+1LL*ad*(a[p].r-a[p].l+1)%mod)%mod; return;} push_down(p);
if(a[p*2].r>=l) add(p*2,l,r,ad); if(a[p*2+1].l<=r) add(p*2+1,l,r,ad); push_up(p);
}
ll search(int p,int l,int r){
if(a[p].l>=l&&a[p].r<=r) return a[p].sum; push_down(p);
ll res=0; if(a[p*2].r>=l) res+=search(p*2,l,r); if(a[p*2+1].l<=r) res=(res+search(p*2+1,l,r))%mod; return res%mod;
}
void tadd(int from,int to){t[++cnt].to=to; t[cnt].nex=head[from]; head[from]=cnt;}
void dfs1(int p,int f){
dep[p]=dep[f]+1; siz[p]=1; fa[p]=f; for(int i=head[p];i;i=t[i].nex) if(t[i].to!=f)
{dfs1(t[i].to,p); siz[p]+=siz[t[i].to]; son[p]=(siz[t[i].to]>siz[son[p]]?t[i].to:son[p]);}
}
void dfs2(int p,int tp){
top[p]=tp; id[p]=++tot; sid[tot]=p; if(!son[p]) return; dfs2(son[p],tp);
for(int i=head[p];i;i=t[i].nex) if(t[i].to!=fa[p]&&t[i].to!=son[p]) dfs2(t[i].to,t[i].to);
}
void t_add(int p1,int p2,int ad){
while(top[p1]!=top[p2]){if(dep[top[p1]]<dep[top[p2]]) swap(p1,p2); add(1,id[top[p1]],id[p1],ad); p1=fa[top[p1]];}
if(dep[p1]>dep[p2]) swap(p1,p2); add(1,id[p1],id[p2],ad);
}
ll t_search(int p1,int p2){
ll res=0; while(top[p1]!=top[p2]){if(dep[top[p1]]<dep[top[p2]]) swap(p1,p2); res=(res+search(1,id[top[p1]],id[p1]))%mod; p1=fa[top[p1]];}
if(dep[p1]>dep[p2]) swap(p1,p2); res=(res+search(1,id[p1],id[p2]))%mod; return res;
}
int main(){
scanf("%d%d%d%d",&n,&m,&root,&mod); for(int i=1;i<=n;i++) scanf("%d",&in[i]);
for(int i=1;i<n;i++){scanf("%d%d",&x,&y); tadd(x,y); tadd(y,x);} dfs1(root,0); dfs2(root,root); build(1,1,n);
while(m--){
scanf("%d",&opt);
if(opt==1){scanf("%d%d%d",&x,&y,&z); t_add(x,y,z);}
else if(opt==2){scanf("%d%d",&x,&y); printf("%lld\n",t_search(x,y));}
else if(opt==3){scanf("%d%d",&x,&y); add(1,id[x],id[x]+siz[x]-1,y);}
else if(opt==4){scanf("%d",&x); printf("%lld\n",search(1,id[x],id[x]+siz[x]-1));}
}
return 0;
}
例 2:P3379 【模板】最近公共祖先(LCA)
题目大意
给定一棵 \(n\) 个点间的树,求出 \(m\) 对点间的 \(\operatorname{LCA}\)。
思路
同例 1 的操作 1、2,不断将 \(u,v\) 往上跳直到位于同一条链,此时深度较小的一个点就是 LCA。
代码
#include<iostream>
#include<cstdio>
#define maxn 500005
using namespace std;
int n,m,root,x,y; int dep[maxn],siz[maxn],fa[maxn],son[maxn],top[maxn],id[maxn],tot=0;
struct node{int to,nex;}a[maxn*2]; int head[maxn],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
void dfs1(int p,int f){
dep[p]=dep[f]+1; siz[p]=1; fa[p]=f; for(int i=head[p];i;i=a[i].nex) if(a[i].to!=f)
{dfs1(a[i].to,p); siz[p]+=siz[a[i].to]; son[p]=(siz[a[i].to]>siz[son[p]]?a[i].to:son[p]);}
}
void dfs2(int p,int tp){
top[p]=tp; id[p]=++tot; if(!son[p]) return; dfs2(son[p],tp);
for(int i=head[p];i;i=a[i].nex) if(a[i].to!=fa[p]&&a[i].to!=son[p]) dfs2(a[i].to,a[i].to);
}
int lca(int p1,int p2){
while(id[top[p1]]!=id[top[p2]]){if(dep[top[p1]]<dep[top[p2]]) swap(p1,p2); p1=fa[top[p1]];}
if(dep[p1]>dep[p2]) return p2; return p1;
}
int main(){
scanf("%d%d%d",&n,&m,&root); for(int i=1;i<n;i++){scanf("%d%d",&x,&y); add(x,y); add(y,x);}
dfs1(root,0); dfs2(root,root); while(m--){scanf("%d%d",&x,&y); printf("%d\n",lca(x,y));}
return 0;
}
例 3:P4114 Qtree1
题目大意
给定一棵 \(n\) 个节点的树,边有边权,有 \(m\) 次操作:修改第 \(x\) 条边的边权为 \(y\) 和查询 \(x\) 到 \(y\) 的简单路径上的边权最大值。
思路
考虑到线段树维护单点而本题修改为边权,于是可以将 \((u,v)\) 的边权放在深度较大的点上,这样就能够解决问题。而查询时仍然将 \(u\) 和 \(v\) 向上跳并统计最终答案,当到一条链上时,由于 \(\operatorname{LCA}\) 的点权不能被算入答案(因为该点权记录 \(\operatorname{LCA}\) 到其父亲的边,而 \((u,v)\) 简单路径不经过这条边),我们应查询深度大的节点到 \(\operatorname{LCA}\) 的 子节点 的最大值,找到这个子节点只需要用 DFN 序连续的性质将 \(\operatorname{LCA}\) 的编号加一即可。
代码
#include<iostream>
#include<cstdio>
#define maxn 100005
using namespace std;
int n,x,y,u[maxn],v[maxn],w[maxn]; struct node{int to,nex;}t[maxn*2]; int head[maxn],cnt=0; char ch[10];
struct seg_tree{int l,r,max;}a[maxn*4];
int dep[maxn],siz[maxn],fa[maxn],son[maxn],top[maxn],id[maxn],tot=0;
void add(int from,int to){t[++cnt].to=to; t[cnt].nex=head[from]; head[from]=cnt;}
void dfs1(int p,int f){
dep[p]=dep[f]+1; siz[p]=1; fa[p]=f; for(int i=head[p];i;i=t[i].nex) if(t[i].to!=f)
{dfs1(t[i].to,p); siz[p]+=siz[t[i].to]; son[p]=(siz[t[i].to]>siz[son[p]]?t[i].to:son[p]);}
}
void dfs2(int p,int tp){
top[p]=tp; id[p]=++tot; if(!son[p]) return; dfs2(son[p],tp);
for(int i=head[p];i;i=t[i].nex) if(t[i].to!=son[p]&&t[i].to!=fa[p]) dfs2(t[i].to,t[i].to);
}
void push_up(int p){a[p].max=max(a[p*2].max,a[p*2+1].max);}
void build(int p,int l,int r){a[p].l=l; a[p].r=r; if(l==r) return; build(p*2,l,(l+r)/2); build(p*2+1,(l+r)/2+1,r);}
void t_add(int p,int l,int ch){if(a[p].l==a[p].r){a[p].max=ch; return;} if(l<=a[p*2].r) t_add(p*2,l,ch); else t_add(p*2+1,l,ch); push_up(p);}
int search(int p,int l,int r){
if(l>r) return 0; if(a[p].l>=l&&a[p].r<=r) return a[p].max; int res=-1;
if(l<=a[p*2].r) res=search(p*2,l,r); if(r>=a[p*2+1].l) res=max(res,search(p*2+1,l,r)); return res;
}
int t_search(int p1,int p2){
int res=0; while(id[top[p1]]!=id[top[p2]]){if(dep[top[p1]]<dep[top[p2]]) swap(p1,p2); res=max(res,search(1,id[top[p1]],id[p1])); p1=fa[top[p1]];}
res=max(res,search(1,min(id[p1],id[p2])+1,max(id[p1],id[p2]))); return res;
}
int main(){
scanf("%d",&n); for(int i=1;i<n;i++){scanf("%d%d%d",&u[i],&v[i],&w[i]); add(u[i],v[i]); add(v[i],u[i]);}
dfs1(1,0); dfs2(1,1); build(1,1,n); for(int i=1;i<=n;i++)
t_add(1,(dep[u[i]]>dep[v[i]]?id[u[i]]:id[v[i]]),w[i]);
while(1){
cin>>ch+1; if(ch[1]=='D') break;
if(ch[1]=='C'){scanf("%d%d",&x,&y); t_add(1,(dep[u[x]]>dep[v[x]]?id[u[x]]:id[v[x]]),y);}
else if(ch[1]=='Q'){scanf("%d%d",&x,&y); printf("%d\n",t_search(x,y));}
}
return 0;
}
例 4:P4116 Qtree3
题目大意
给定一棵有 \(n\) 个点的树,每个点有颜色,初始全白。两种操作:将 \(x\) 反色(白变黑,黑变白)和查询 \(1\) 到 \(x\) 路径上第一个黑点的编号。
思路
将 \(1\) 视作根,那么 \(1\) 到 \(x\) 的路径上的点的编号一定递增,故将所有黑点的权值看作 DFN 序,白点权值看作正无穷,树剖 + 线段树维护最小值即可。
代码
#include<iostream>
#include<cstdio>
#define maxn 100005
#define inf 50000005
using namespace std;
int n,q,opt,u,v,col[maxn]; struct node{int to,nex;}t[maxn*2]; int head[maxn],cnt=0;
int dep[maxn],siz[maxn],fa[maxn],son[maxn],top[maxn],id[maxn],tot=0,sid[maxn];
int min(int xx,int yy){return xx<yy?xx:yy;}
void add(int from,int to){t[++cnt].to=to; t[cnt].nex=head[from]; head[from]=cnt;}
void dfs1(int p,int f){
dep[p]=dep[f]+1; siz[p]=1; fa[p]=f; for(int i=head[p];i;i=t[i].nex) if(t[i].to!=f)
{dfs1(t[i].to,p); siz[p]+=siz[t[i].to]; son[p]=(siz[t[i].to]>siz[son[p]]?t[i].to:son[p]);}
}
void dfs2(int p,int tp){
top[p]=tp; id[p]=++tot; sid[tot]=p; if(!son[p]) return; dfs2(son[p],tp);
for(int i=head[p];i;i=t[i].nex) if(t[i].to!=fa[p]&&t[i].to!=son[p]) dfs2(t[i].to,t[i].to);
}
struct seg_tree{int l,r,min;}a[maxn*4]; void push_up(int p){a[p].min=min(a[p*2].min,a[p*2+1].min);}
void build(int p,int l,int r){a[p].l=l; a[p].r=r; a[p].min=inf; if(l==r) return; build(p*2,l,(l+r)/2); build(p*2+1,(l+r)/2+1,r);}
void change(int p,int l,int ch){if(a[p].l==a[p].r){a[p].min=ch; return;} if(l<=a[p*2].r) change(p*2,l,ch); else change(p*2+1,l,ch); push_up(p);}
int search(int p,int l,int r){
if(l>r) return inf; if(a[p].l>=l&&a[p].r<=r) return a[p].min; int res=inf;
if(l<=a[p*2].r) res=search(p*2,l,r); if(r>=a[p*2+1].l) res=min(res,search(p*2+1,l,r)); return res;
}
int t_search(int p1,int p2){
int res=inf; while(id[top[p1]]!=id[top[p2]]){if(dep[top[p1]]<dep[top[p2]]) swap(p1,p2); res=min(res,search(1,id[top[p1]],id[p1])); p1=fa[top[p1]];}
res=min(res,search(1,min(id[p1],id[p2]),max(id[p1],id[p2]))); return res;
}
int main(){
scanf("%d%d",&n,&q); for(int i=1;i<n;i++){scanf("%d%d",&u,&v); add(u,v); add(v,u);}
dfs1(1,0); dfs2(1,1); build(1,1,n);
while(q--){
scanf("%d%d",&opt,&u);
if(!opt){if(col[u]==0){col[u]=1; change(1,id[u],id[u]);} else{col[u]=0; change(1,id[u],inf);}}
else printf("%d\n",((t_search(1,u)==inf)?-1:sid[t_search(1,u)]));
}
return 0;
}
例 5:P2590 [ZJOI2008] 树的统计
题目大意
类似 Qtree1,给定一棵 \(n\) 个节点的树,点有点权,有 \(m\) 次操作:修改第 \(x\) 个点的点权为 \(y\) 、查询 \(x\) 到 \(y\) 的简单路径上的点权最大值或点权和。
思路
树剖完线段树维护即可。
代码
#include<iostream>
#include<cstdio>
#define maxn 30005
#define inf 1000000000
using namespace std;
int n,u,v,T,w[maxn]; char opt[10]; struct edge{int to,nex;}eg[maxn*2]; int head[maxn],cnt=0;
void add(int from,int to){eg[++cnt].to=to; eg[cnt].nex=head[from]; head[from]=cnt;}
int siz[maxn],fa[maxn],dep[maxn],son[maxn],top[maxn],dfn[maxn],dfncnt=0,inv[maxn];
void dfs1(int p,int f){
fa[p]=f; siz[p]=1; dep[p]=dep[f]+1; for(int i=head[p];i;i=eg[i].nex) if(eg[i].to!=f)
{dfs1(eg[i].to,p); siz[p]+=siz[eg[i].to]; son[p]=(siz[eg[i].to]>siz[son[p]]?eg[i].to:son[p]);}
}
void dfs2(int p,int tp){
top[p]=tp; dfn[p]=++dfncnt; inv[dfncnt]=p; if(son[p]) dfs2(son[p],tp);
for(int i=head[p];i;i=eg[i].nex) if(eg[i].to!=fa[p]&&eg[i].to!=son[p]) dfs2(eg[i].to,eg[i].to);
}
struct node{int l,r,sum,max;}a[maxn*4];
void pushup(int p){a[p].sum=a[p<<1].sum+a[p<<1|1].sum; a[p].max=max(a[p<<1].max,a[p<<1|1].max);}
void build(int p,int l,int r){
a[p].l=l; a[p].r=r; if(l==r){a[p].sum=a[p].max=w[inv[l]]; return;}
build(p<<1,l,(l+r)>>1); build(p<<1|1,((l+r)>>1)+1,r); pushup(p);
}
void modify(int p,int pos,int x){
if(a[p].l==a[p].r){a[p].sum=a[p].max=x; return;}
if(pos<=a[p<<1].r) modify(p<<1,pos,x); else modify(p<<1|1,pos,x); pushup(p);
}
int q_max(int p,int l,int r){
if(a[p].l>=l&&a[p].r<=r) return a[p].max; int res=-inf;
if(l<=a[p<<1].r) res=q_max(p<<1,l,r); if(r>=a[p<<1|1].l) res=max(res,q_max(p<<1|1,l,r)); return res;
}
int q_sum(int p,int l,int r){
if(a[p].l>=l&&a[p].r<=r) return a[p].sum; int res=0;
if(l<=a[p<<1].r) res=q_sum(p<<1,l,r); if(r>=a[p<<1|1].l) res+=q_sum(p<<1|1,l,r); return res;
}
int query_max(int p1,int p2){
int res=-inf; while(top[p1]!=top[p2])
{if(dep[top[p1]]<dep[top[p2]]) swap(p1,p2); res=max(res,q_max(1,dfn[top[p1]],dfn[p1])); p1=fa[top[p1]];}
if(dep[p1]<dep[p2]) swap(p1,p2); res=max(res,q_max(1,dfn[p2],dfn[p1])); return res;
}
int query_sum(int p1,int p2){
int res=0; while(top[p1]!=top[p2])
{if(dep[top[p1]]<dep[top[p2]]) swap(p1,p2); res+=q_sum(1,dfn[top[p1]],dfn[p1]); p1=fa[top[p1]];}
if(dep[p1]<dep[p2]) swap(p1,p2); res+=q_sum(1,dfn[p2],dfn[p1]); return res;
}
int main(){
scanf("%d",&n); for(int i=1;i<n;i++) scanf("%d%d",&u,&v),add(u,v),add(v,u);
for(int i=1;i<=n;i++) scanf("%d",&w[i]); dfs1(1,0); dfs2(1,1); build(1,1,n);
scanf("%d",&T); while(T--){
scanf("%s%d%d",opt+1,&u,&v); if(opt[2]=='H') modify(1,dfn[u],v);
else if(opt[2]=='M') printf("%d\n",query_max(u,v)); else printf("%d\n",query_sum(u,v));
} return 0;
}
例 5:P4216 [SCOI2015] 情报传递
题目大意
给定一棵树,每个点有点权,初始全为 \(0\)。要支持两个操作:给一个点打上标记,本次操作后该点每一次操作前权值加一;或是询问 \(u\rightarrow v\) 的路径上的总点数和权值大于 \(c\) 的点数。
思路
询问时,总点数很好处理,权值大于 \(c\) 的点数即查询路径上打标记先于第 \(id-c\) 个操作的点数(\(id\) 为询问编号)。于是按照询问的 \(id-c\) 排序,离线下来处理即可。
代码
#include<iostream>
#include<cstdio>
#include<algorithm>
#define maxn 200005
#define pii pair<int,int>
#define m_p make_pair
#define a_f first
#define a_s second
using namespace std;
int n,rt,x,T,pos1,pos2; struct ques{int id,opt,u,v,c; pii ans;}q[maxn]; bool cmp2(ques aa,ques bb){return aa.id<bb.id;}
bool cmp1(ques aa,ques bb){return aa.opt==bb.opt?(aa.opt==1?((aa.id-aa.c)<(bb.id-bb.c)):(aa.id<bb.id)):aa.opt<bb.opt;}
struct edge{int to,nex;}e[maxn]; int head[maxn],cnt=0;
void add(int from,int to){e[++cnt].to=to; e[cnt].nex=head[from]; head[from]=cnt;}
int c[maxn]; int lowbit(int x){return x&(-x);} void modify(int p){for(;p<=n;p+=lowbit(p)) c[p]++;}
int search(int p){int res=0; for(;p>=1;p-=lowbit(p)) res+=c[p]; return res;}
int fa[maxn],siz[maxn],son[maxn],dep[maxn],top[maxn],dfn[maxn],dfncnt=0;
void dfs1(int p,int f){
fa[p]=f; siz[p]=1; dep[p]=dep[f]+1; for(int i=head[p];i;i=e[i].nex) if(e[i].to!=f)
{dfs1(e[i].to,p); siz[p]+=siz[e[i].to]; son[p]=siz[e[i].to]>siz[son[p]]?e[i].to:son[p];}
}
void dfs2(int p,int tp){
top[p]=tp; dfn[p]=++dfncnt; if(son[p]) dfs2(son[p],tp);
for(int i=head[p];i;i=e[i].nex) if(e[i].to!=fa[p]&&e[i].to!=son[p]) dfs2(e[i].to,e[i].to);
}
pii query(int p1,int p2){
int depsum=dep[p1]+dep[p2]; int res=0; while(dfn[top[p1]]!=dfn[top[p2]])
{if(dep[top[p1]]<dep[top[p2]]) swap(p1,p2); res+=search(dfn[p1])-search(dfn[top[p1]]-1); p1=fa[top[p1]];}
if(dep[p1]<dep[p2]) swap(p1,p2); res+=search(dfn[p1])-search(dfn[p2]-1); return m_p(depsum-2*dep[p2]+1,res);
}
int main(){
scanf("%d",&n); for(int i=1;i<=n;i++){scanf("%d",&x); if(x==0) rt=i; else add(x,i);} scanf("%d",&T);
for(int i=1;i<=T;i++){scanf("%d%d",&q[i].opt,&q[i].u); q[i].id=i; if(q[i].opt==1) pos2++,scanf("%d%d",&q[i].v,&q[i].c);}
sort(q+1,q+1+T,cmp1); pos1=1; int respos=pos2; pos2++; dfs1(rt,0); dfs2(rt,rt); while(pos1<=respos){
while(pos2<=T&&q[pos2].id<(q[pos1].id-q[pos1].c)) modify(dfn[q[pos2].u]),pos2++;
while(pos1<=respos&&(q[pos2].id>=(q[pos1].id-q[pos1].c)||pos2>T)) q[pos1].ans=query(q[pos1].u,q[pos1].v),pos1++;
} sort(q+1,q+1+T,cmp2); for(int i=1;i<=T;i++) if(q[i].opt==1) printf("%d %d\n",q[i].ans.a_f,q[i].ans.a_s);
return 0;
}


