线段树进阶

线段树

权值线段树

对于一类问题，我们只关心每种元素出现的次数，所以就诞生了权值线段树：我们用线段树的叶子节点维护对应元素出现的次数，那么就可以统计 \([l,r]\) 区间内的数一共出现了多少次了。如下图。

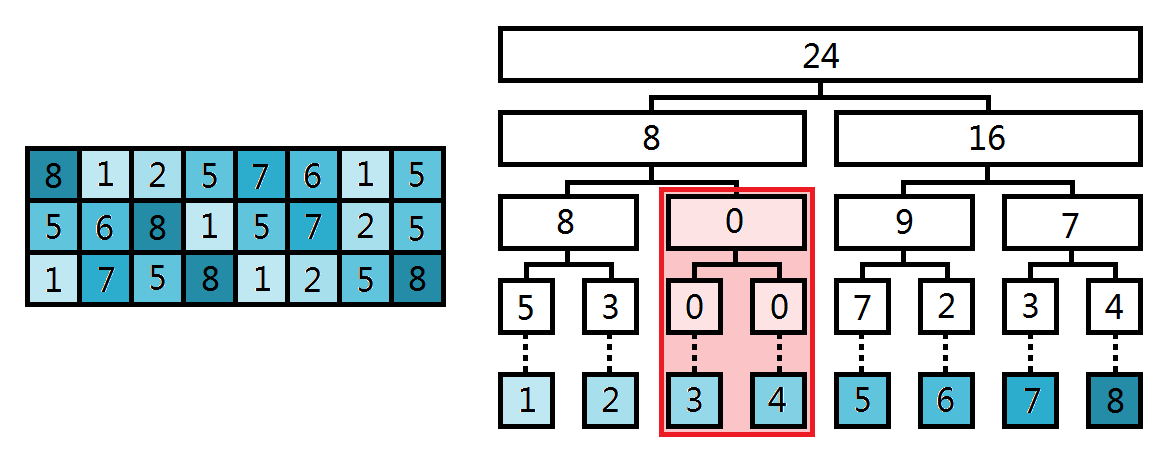
动态开点

普通的权值线段树会浪费很大空间，如上图红色框起来的部分，而动态开点的线段树就可以避免许多空间的浪费。正因为权值一般范围比较大，直接像原来那样开四倍空间的话空间复杂度不能承受，故我们随用随开，节省空间。

具体地，我们在使用时维护每个节点的信息以及左右儿子，若使用时记录的左右儿子为 \(0\) 则可以新开一个点存进去。

线段树合并

顾名思义，我们只需要将两棵线段树对应的部分合并即可（假设现在合并 \(p_1,p_2\) 两点，值域为 \([l,r]\)）（下面都将树合并至 \(p_1\)，实际上合并到 \(p_2\) 也是可以的）：

• 假如 \(p_1\) 或 \(p_2\) 为空，代表有一棵树不存在，直接返回另一棵树；

• 假如 \(l = r\)，代表合并到叶子节点了，直接暴力合并两点到 \(p_1\) 再返回即可；

• 假如 \(l < r\)，那么递归合并左右两棵子树到 \(p_1\)，最后更新 \(p_1\) 再返回即可。

下用例题来具体阐述。

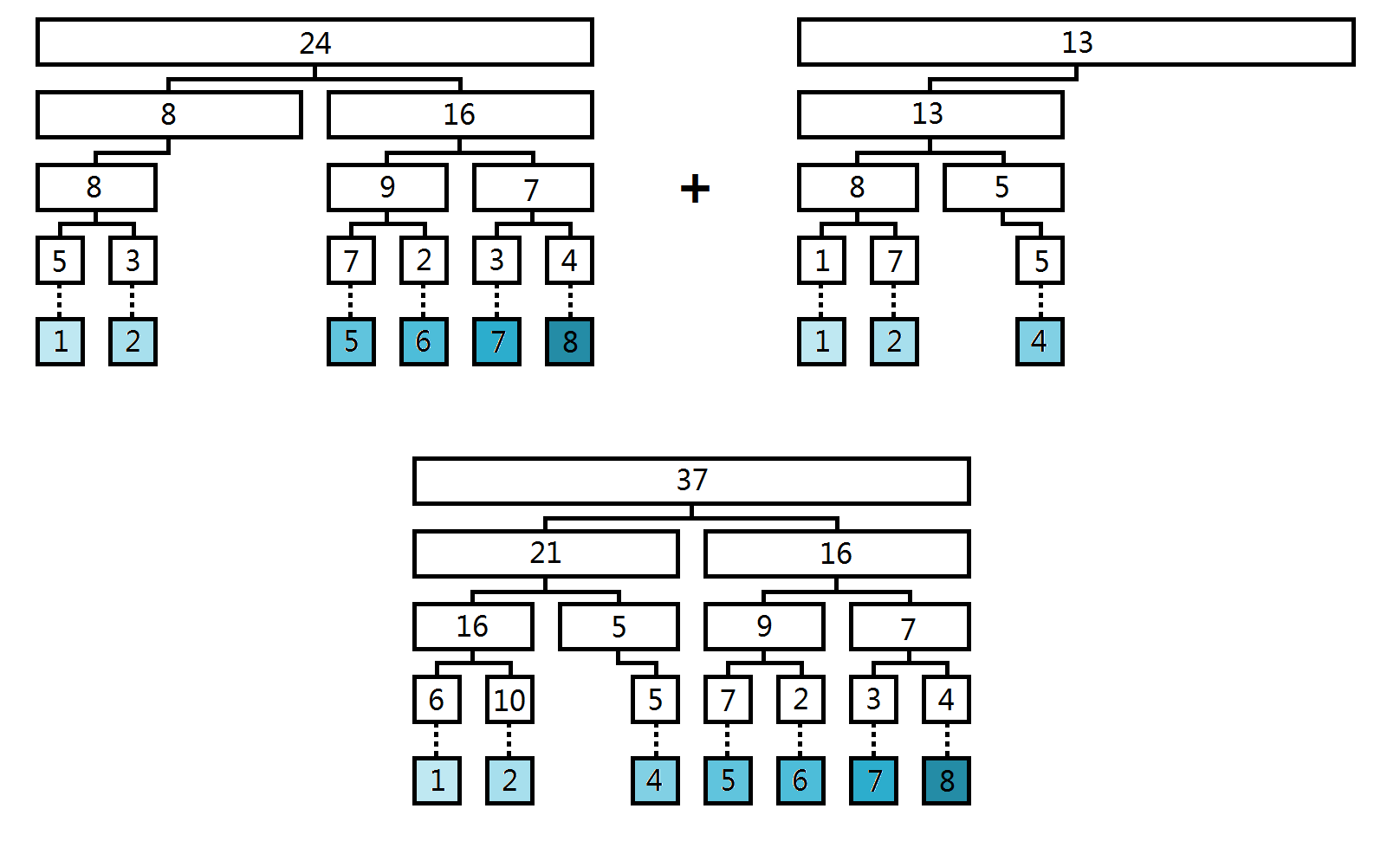
例题

例 1 ： CF600E / CF600E Lomsat gelral

题目大意

有一棵以 \(1\) 为根的节点数为 \(n\) 的树，每个节点有颜色，以编号 \(c_i\)（\(1\le c_i\le n\)）表示，求以每个点为根的子树内出现次数最多的颜色（可能多个）的编号和。

思路

我们对颜色建立权值线段树维护每个节点出现最多的颜色出现的次数和编号之和。DFS 一遍整棵树，对于一个节点，其可以将所有子树的线段树合并来得到这个节点的答案，因为是 DFS 过程，遍历到某个节点时一定会将以其为根的整个子树都合并到该点，故可以维护整个子树内的信息。剩下的都是线段树的基础维护操作。

#include<iostream>
#include<cstdio>
#define maxn 100005
#define maxp 2000005
#define ll long long
using namespace std;
int n,col[maxn],u,v; ll ans[maxn]; struct node{int to,nex;}t[maxn*2]; int head[maxn],cnt=0;
void add(int from,int to){t[++cnt].to=to; t[cnt].nex=head[from]; head[from]=cnt;}
int tot=0,root[maxn]; struct seg_tree{int l,r,ti; ll ans;}a[maxp]; // 'ti' -> frequency  'ans' -> sum of the colors 
void push_up(int p){
	if(a[a[p].l].ti==a[a[p].r].ti){a[p].ti=a[a[p].l].ti; a[p].ans=a[a[p].l].ans+a[a[p].r].ans;}
	else{if(a[a[p].l].ti>a[a[p].r].ti){a[p].ti=a[a[p].l].ti; a[p].ans=a[a[p].l].ans;} else{a[p].ti=a[a[p].r].ti; a[p].ans=a[a[p].r].ans;}}
}
void insert(int &p,int l,int r,int col){ // add a node with color 'col' at position 'p'  
	if(!p) p=++tot; if(l==r){a[p].ans=l; a[p].ti++; return;}
	if(col<=(l+r)/2) insert(a[p].l,l,(l+r)/2,col); else insert(a[p].r,(l+r)/2+1,r,col); push_up(p);
}
int merge(int p1,int p2,int l,int r){ // merge the node 'p1' and 'p2' 
	if((!p1)||(!p2)) return p1+p2; if(l==r){a[p1].ti+=a[p2].ti; return p1;}
	a[p1].l=merge(a[p1].l,a[p2].l,l,(l+r)/2); a[p1].r=merge(a[p1].r,a[p2].r,(l+r)/2+1,r); push_up(p1); return p1;
}
void dfs(int p,int fa){
	for(int i=head[p];i;i=t[i].nex){if(t[i].to==fa) continue; dfs(t[i].to,p); root[p]=merge(root[p],root[t[i].to],1,n);}
	insert(root[p],1,n,col[p]); ans[p]=a[root[p]].ans;
}
int main(){
	scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&col[i]); for(int i=1;i<n;i++){scanf("%d%d",&u,&v); add(u,v); add(v,u);}
	dfs(1,-1); for(int i=1;i<=n;i++) printf("%lld ",ans[i]);
	return 0;
}

例 2 ： P3605 [USACO17JAN]Promotion Counting P

题目大意

有一棵以 \(1\) 为根的节点数为 \(n\) 的树，每个节点有一个权值 \(p_i\)（\(1\le pi\le 10^9\)），求以每个点为根的子树内有多少个点的权值大于该子树的根。

思路

显然直接建权值线段树空间很大，考虑离散化权值之后建权值线段树，之后 DFS + 合并 + 区间和查询（大体同例 1）得到答案。

#include<iostream>
#include<cstdio>
#include<algorithm>
#define maxn 100005
#define maxp 2000005
using namespace std;
int n,u,v[maxn],ls[maxn],ans[maxn]; struct node{int to,nex;}t[maxn*2]; int head[maxn],cnt=0;
void add(int from,int to){t[++cnt].to=to; t[cnt].nex=head[from]; head[from]=cnt;}
int tot=0,root[maxn]; struct seg_tree{int l,r,ans;}a[maxp]; void push_up(int p){a[p].ans=a[a[p].l].ans+a[a[p].r].ans;}
void insert(int &p,int l,int r,int num){
	if(!p) p=++tot; if(l==r){a[p].ans++; return;}
	if(num<=(l+r)/2) insert(a[p].l,l,(l+r)/2,num); else insert(a[p].r,(l+r)/2+1,r,num); push_up(p);
}
int merge(int p1,int p2,int l,int r){
	if((!p1)||(!p2)) return p1+p2; if(l==r){a[p1].ans+=a[p2].ans; return p1;}
	a[p1].l=merge(a[p1].l,a[p2].l,l,(l+r)/2); a[p1].r=merge(a[p1].r,a[p2].r,(l+r)/2+1,r); push_up(p1); return p1;
}
int search(int p,int l,int r,int num){
	if(p==0) return 0; if(l>=num) return a[p].ans;
	int res=0; if(num<=(l+r)/2) res=search(a[p].l,l,(l+r)/2,num); if((l+r)/2+1<=n) res+=search(a[p].r,(l+r)/2+1,r,num); return res;
}
void dfs(int p,int fa){
	for(int i=head[p];i;i=t[i].nex){if(t[i].to==fa) continue; dfs(t[i].to,p); root[p]=merge(root[p],root[t[i].to],1,n);}
	insert(root[p],1,n,v[p]); ans[p]=search(root[p],1,n,v[p]+1);
}
int main(){
	scanf("%d",&n); for(int i=1;i<=n;i++){scanf("%d",&v[i]); ls[i]=v[i];} for(int i=2;i<=n;i++){scanf("%d",&u); add(i,u); add(u,i);}
	sort(ls+1,ls+1+n); int lenth=unique(ls+1,ls+1+n)-ls-1; for(int i=1;i<=n;i++) v[i]=lower_bound(ls+1,ls+1+lenth,v[i])-ls;
	dfs(1,-1); for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
	return 0;
}

例 3 ： P3224 [HNOI2012]永无乡

题目大意

有 \(n\) 个点初始由 \(m\) 条边连接，每个点有排名 \(p_i\)（\(p\) 为一个 \(1\sim n\) 的排列）。两种操作，一种是连一条边，一种是查询 \(x\) 的联通块内排名第 \(k\) 小的。

思路

看到联通块想到用并查集维护。每个点开一棵权值线段树存排名，并查集合并时也将线段树合并，查询时查询当前联通块的线段树即可。

#include<iostream>
#include<cstdio>
#define maxn 100005
#define maxp 2000005
using namespace std;
int n,m,u,v,q,f[maxn],cor[maxn]; char ch; int getfa(int xx){if(f[xx]==xx) return xx; return f[xx]=getfa(f[xx]);}
int root[maxn],tot=0; struct seg_tree{int l,r,ans;}a[maxp];
void push_up(int p){a[p].ans=a[a[p].l].ans+a[a[p].r].ans;}
void insert(int &p,int l,int r,int num){
	if(!p) p=++tot; if(l==r){a[p].ans++; return;}
	if(num<=(l+r)/2) insert(a[p].l,l,(l+r)/2,num); else insert(a[p].r,(l+r)/2+1,r,num); push_up(p);
}
int merge(int p1,int p2,int l,int r){
	if((!p1)||(!p2)) return p1+p2; if(l==r){a[p1].ans+=a[p2].ans; return p1;}
	a[p1].l=merge(a[p1].l,a[p2].l,l,(l+r)/2); a[p1].r=merge(a[p1].r,a[p2].r,(l+r)/2+1,r); push_up(p1); return p1;
}
int getrank(int p,int l,int r,int rnk){
	if(rnk>a[p].ans) return 0; if(l==r) return l;
	if(rnk<=a[a[p].l].ans) return getrank(a[p].l,l,(l+r)/2,rnk); return getrank(a[p].r,(l+r)/2+1,r,rnk-a[a[p].l].ans);
}
void build(int u,int v){int r1=getfa(u),r2=getfa(v); if(r1!=r2){f[r2]=r1; root[r1]=merge(root[r1],root[r2],1,n);}}
int main(){
	cor[0]=-1; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){f[i]=i; scanf("%d",&u); cor[u]=i; insert(root[i],1,n,u);}
	for(int i=1;i<=m;i++){scanf("%d%d",&u,&v); build(u,v);}
	scanf("%d",&q); while(q--){scanf("\n%c%d%d",&ch,&u,&v); if(ch=='B') build(u,v); else printf("%d\n",cor[getrank(root[getfa(u)],1,n,v)]);}
	return 0;
}

例 4 ： POI2011 S2D2 / P3521 [POI2011]ROT-Tree Rotations

题目大意

有一棵 \(n\) 个叶子的二叉树，每个叶子有一个权值（所有权值构成 \(1\sim n\) 的排列），每个非叶子节点一定有两个儿子。现在可以任意交换每个点的左右儿子，求先序遍历得到的叶子节点权值构成的序列的逆序对个数最小值。

思路

显然交换左右子树只会影响这个子树内部的逆序对个数，即 \(\cdots[\cdots(left)][\cdots(right)]\cdots\) 和 \(\cdots[\cdots(right)][\cdots(left)]\cdots\) 的差别（\(left\) 表示左子树而 \(right\) 表示右子树），所以可以对于每个叶子建权值线段树，每个节点贪心考虑换不换并合并线段树即可。换不换可以分别计算值并比较，具体地，对于权值线段树的 \([l,mid]\) 和 \([mid+1,r]\) 区段，不换的逆序对个数即为 \(\sum\limits\min{(\operatorname{size}(left,[mid+1,r])*\operatorname{size}(right,[l,mid]))}\)。

#include<iostream>
#include<cstdio>
#define maxn 200005
#define maxp 4000005
#define ll long long
using namespace std;
int n; ll ans=0,ro,nro; int root[maxn],cnt=0,tot=0; struct node{int l,r,ans;}a[maxp]; void push_up(int p){a[p].ans=a[a[p].l].ans+a[a[p].r].ans;}
void insert(int &p,int l,int r,int num){
	if(!p) p=++tot; if(l==r){a[p].ans++; return;}
	if(num<=(l+r)/2) insert(a[p].l,l,(l+r)/2,num); else insert(a[p].r,(l+r)/2+1,r,num); push_up(p);
}
int merge(int p1,int p2,int l,int r){
	if((!p1)||(!p2)) return p1+p2; if(l==r){a[p1].ans+=a[p2].ans; return p1;}
	nro+=(1LL*a[a[p1].r].ans*a[a[p2].l].ans); ro+=(1LL*a[a[p1].l].ans*a[a[p2].r].ans);
	a[p1].l=merge(a[p1].l,a[p2].l,l,(l+r)/2); a[p1].r=merge(a[p1].r,a[p2].r,(l+r)/2+1,r); push_up(p1); return p1;
}
int dfs(){
	int tmp,pos=0; scanf("%d",&tmp);
	if(!tmp){int left=dfs(),right=dfs(); ro=nro=0; pos=merge(left,right,1,n); ans+=min(ro,nro); return pos;}
	else{insert(root[++cnt],1,n,tmp); return root[cnt];}
}
int main(){
	scanf("%d",&n); dfs(); printf("%lld",ans);
	return 0;
}

例 5 ： P4556 [Vani有约会]雨天的尾巴 /【模板】线段树合并

题目大意

有一棵树，有 \(m\) 次操作，每次给出 \(x,y,z\)，表示从 \(x,y\) 的简单路径上的每一个点都增加一个编号为 \(z\) 的物品。求所有操作后每个点的物品数量最多的物品的编号，若多个物品数量相等取编号最小的。

思路

看到简单路径考虑 \(\operatorname{LCA}\)，考虑树上差分，给每一个点开一棵权值线段树，操作即为给 \(u\) 和 \(v\) 对应编号的物品加一并将 \(\operatorname{LCA}(u,v)\) 和其父亲对应编号的物品减一，最后自下往上合并即可求出答案。

#include<iostream>
#include<cstdio>
#define maxn 100005
#define maxp 2000005
using namespace std;
int n,m,u,v,w,z,log[maxn],dep[maxn],st[maxn][20],ans[maxn]; struct node{int to,nex;}t[maxn*2]; int head[maxn],cnt=0;
void add(int from,int to){t[++cnt].to=to; t[cnt].nex=head[from]; head[from]=cnt;}
int root[maxn],tot=0; struct seg_tree{int l,r,ans,typ;}a[maxp];
void dfs_set(int p,int fa){
	st[p][0]=fa; dep[p]=dep[fa]+1; for(int i=1;i<=log[dep[p]];i++) st[p][i]=st[st[p][i-1]][i-1];
	for(int i=head[p];i;i=t[i].nex) if(t[i].to!=fa) dfs_set(t[i].to,p);
}
int lca(int p,int q){
	if(dep[p]<dep[q]) swap(p,q); while(dep[p]>dep[q]) p=st[p][log[dep[p]-dep[q]]]; if(p==q) return p;
	for(int i=log[dep[p]];i>=0;i--) if(st[p][i]!=st[q][i]){p=st[p][i]; q=st[q][i];} return st[p][0];
}
void push_up(int p){
	if(a[a[p].l].typ==a[a[p].r].typ){a[p].typ=a[a[p].l].typ; a[p].ans=a[a[p].l].ans+a[a[p].r].ans;}
	else{
		if(a[a[p].l].ans>a[a[p].r].ans){a[p].typ=a[a[p].l].typ; a[p].ans=a[a[p].l].ans;}
		else if(a[a[p].l].ans==a[a[p].r].ans){a[p].typ=min(a[a[p].l].typ,a[a[p].r].typ); a[p].ans=a[a[p].l].ans;} else{a[p].typ=a[a[p].r].typ; a[p].ans=a[a[p].r].ans;}
	}
}
void insert(int &p,int l,int r,int num,int add){
	if(!p) p=++tot; if(l==r){a[p].typ=l; a[p].ans+=add; return;}
	if(num<=(l+r)/2) insert(a[p].l,l,(l+r)/2,num,add); else insert(a[p].r,(l+r)/2+1,r,num,add); push_up(p);
}
int merge(int p1,int p2,int l,int r){
	if((!p1)||(!p2)) return p1+p2; if(l==r){a[p1].ans+=a[p2].ans; return p1;}
	a[p1].l=merge(a[p1].l,a[p2].l,l,(l+r)/2); a[p1].r=merge(a[p1].r,a[p2].r,(l+r)/2+1,r); push_up(p1); return p1;
}
void dfs(int p,int fa){for(int i=head[p];i;i=t[i].nex){ if(t[i].to==fa) continue; dfs(t[i].to,p); root[p]=merge(root[p],root[t[i].to],1,100000); } ans[p]=a[root[p]].typ;}
int main(){
	scanf("%d%d",&n,&m); for(int i=1;i<n;i++){scanf("%d%d",&u,&v); add(u,v); add(v,u); log[i+1]=log[i]+((1<<(log[i]+1))==(i+1));}
	dfs_set(1,0); while(m--){scanf("%d%d%d",&u,&v,&z); w=lca(u,v); insert(root[u],1,100000,z,1); insert(root[v],1,100000,z,1); insert(root[w],1,100000,z,-1); insert(root[st[w][0]],1,100000,z,-1);}
	dfs(1,0); for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
	return 0;
}

例 6 ： P1600 [NOIP2016 提高组] 天天爱跑步

题目大意

有一棵 \(n\) 个节点的数，给定 \(m\) 对点 \((s_i,t_i)\)，表示从 \(0\) 时刻起会有一个人从 \(s_i\) 开始，以每秒一条边的速度沿 \(s_i\) 和 \(t_i\) 间的简单路径由 \(s_i\) 向 \(t_i\) 移动，到达点 \(t_i\) 的后一秒就消失。对于每个点给定一个 \(w_i\)，求第 \(w_i\) 秒时这个点有几个人。

思路

非常类似于模板题（即例 5）。

一条简单路径一定包含了 \(s\rightarrow \operatorname{LCA}\) 和 \(\operatorname{LCA} \rightarrow t\) 的两部分。

• 对于 \(s\rightarrow \operatorname{LCA}\) 路径上的点 \(p\)，一定满足 \(dep_s - dep_p = w_p\)（\(dep\) 表示深度），即 \(dep_s = dep_p + w_p\)；

• 对于 \(\operatorname{LCA} \rightarrow t\) 路径上的点 \(q\)，一定满足 \(dis_{s,t} - (dep_t - dep_q) = w_q\)（\(dis_{s,t}\) 表示 \(s,t\) 两点间简单路径的长度），即 \(dep_t - dis_{s,t} = dep_q - w_q\)。又因为 \(dis_{s,t} = dep_s + dep_t - 2\times dep_{\operatorname{LCA}}\)，代入得到 \(2\times dep_{\operatorname{LCA}} - dep_s = dep_q - w_q\)。

我们发现一个点能否看到某个人只与以其为根的子树内的起点或终点有关，考虑使用线段树合并。每个点建一棵权值线段树，对于一个起点，将 \(s\) 点的 \(dep_s\) 加一，将 \(t\) 点的 \(2\times dep_{\operatorname{LCA}} - dep_s\) 加一，并在 \(\operatorname{LCA}\) 和其父亲处分别减一（参考板题）。之后只要 DFS 并合并统计即可。

特别注意，首先考虑到 \(2\times dep_{\operatorname{LCA}} - dep_s\) 可能为负值但是范围一定在 \([-n,n]\) 之内，所以将权值线段树的值域整体平移 \(n\) 位解决即可，而查询或修改时遇到超出值域的应直接跳过不做处理以免出问题。而且每个点的答案应该是编号 \(dep[p]+w[p]\) 和 \(dep[p]-w[p]\) 的元素个数之和，而若 \(w_p = 0\) 就只需要统计一个即可（统计两次就重复了）。

不会有人 LCA 打挂了调了一个小时才发现吧

#include<iostream>
#include<cstdio>
#define maxn 600005
#define maxp 8000005
using namespace std;
int n,m,u,v,w[maxn],ans[maxn],log[maxn],dep[maxn],st[maxn][25]; struct node{int to,nex;}t[maxn*2]; int head[maxn],cnt=0;
void add(int from,int to){t[++cnt].to=to; t[cnt].nex=head[from]; head[from]=cnt;}
int root[maxn],tot=0; struct seg_tree{int l,r,sum;}a[maxp]; void push_up(int p){a[p].sum=a[a[p].l].sum+a[a[p].r].sum;}
void dfs_set(int p,int fa){
	dep[p]=dep[fa]+1; st[p][0]=fa; for(int i=1;i<=log[dep[p]];i++) st[p][i]=st[st[p][i-1]][i-1];
	for(int i=head[p];i;i=t[i].nex) if(t[i].to!=fa) dfs_set(t[i].to,p);
}
int lca(int p,int q){
	if(dep[p]<dep[q]) swap(p,q); while(dep[p]>dep[q]) p=st[p][log[dep[p]-dep[q]]]; if(p==q) return p;
	for(int i=log[dep[p]];i>=0;i--) if(st[p][i]!=st[q][i]){p=st[p][i]; q=st[q][i];} return st[p][0];
}
void insert(int &p,int l,int r,int num,int add){
	if(num>2*n||num<0) return; if(!p) p=++tot; if(l==r){a[p].sum+=add; return;}
	if(num<=(l+r)/2) insert(a[p].l,l,(l+r)/2,num,add); else insert(a[p].r,(l+r)/2+1,r,num,add); push_up(p);
}
int search(int p,int l,int r,int num){
	if(l==r) return a[p].sum; if(num<=(l+r)/2) return search(a[p].l,l,(l+r)/2,num); return search(a[p].r,(l+r)/2+1,r,num);
}
int merge(int p1,int p2,int l,int r){
	if((!p1)||(!p2)) return p1+p2; if(l==r){a[p1].sum+=a[p2].sum; return p1;}
	a[p1].l=merge(a[p1].l,a[p2].l,l,(l+r)/2); a[p1].r=merge(a[p1].r,a[p2].r,(l+r)/2+1,r); push_up(p1); return p1;
}
void dfs(int p,int fa){
	for(int i=head[p];i;i=t[i].nex) if(t[i].to!=fa){dfs(t[i].to,p); root[p]=merge(root[p],root[t[i].to],1,2*n);}
	if(dep[p]+w[p]>n&&dep[p]-w[p]<-n) ans[p]=0; else if(dep[p]+w[p]>n) ans[p]=search(root[p],1,2*n,dep[p]-w[p]+n);
	else if(dep[p]-w[p]<-n) ans[p]=search(root[p],1,2*n,dep[p]+w[p]+n);
	else ans[p]=search(root[p],1,2*n,dep[p]+w[p]+n)+(w[p]!=0?search(root[p],1,2*n,dep[p]-w[p]+n):0);
}
int main(){
//	freopen("P1600_17.in","r",stdin); freopen("1.out","w",stdout);
	scanf("%d%d",&n,&m); for(int i=1;i<n;i++){scanf("%d%d",&u,&v); add(u,v); add(v,u); log[i+1]=log[i]+((1<<(log[i]+1))==(i+1));}
	for(int i=1;i<=n;i++) scanf("%d",&w[i]); dfs_set(1,0);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&u,&v); int l=lca(u,v);
		insert(root[u],1,2*n,dep[u]+n,1); insert(root[st[l][0]],1,2*n,dep[u]+n,-1);
		insert(root[v],1,2*n,2*dep[l]-dep[u]+n,1); insert(root[l],1,2*n,2*dep[l]-dep[u]+n,-1);
	} dfs(1,0); for(int i=1;i<=n;i++) printf("%d ",ans[i]);
	return 0;
}
/*
3 2
1 2
2 3
0 1 2
1 3
3 1
*/

线段树分裂

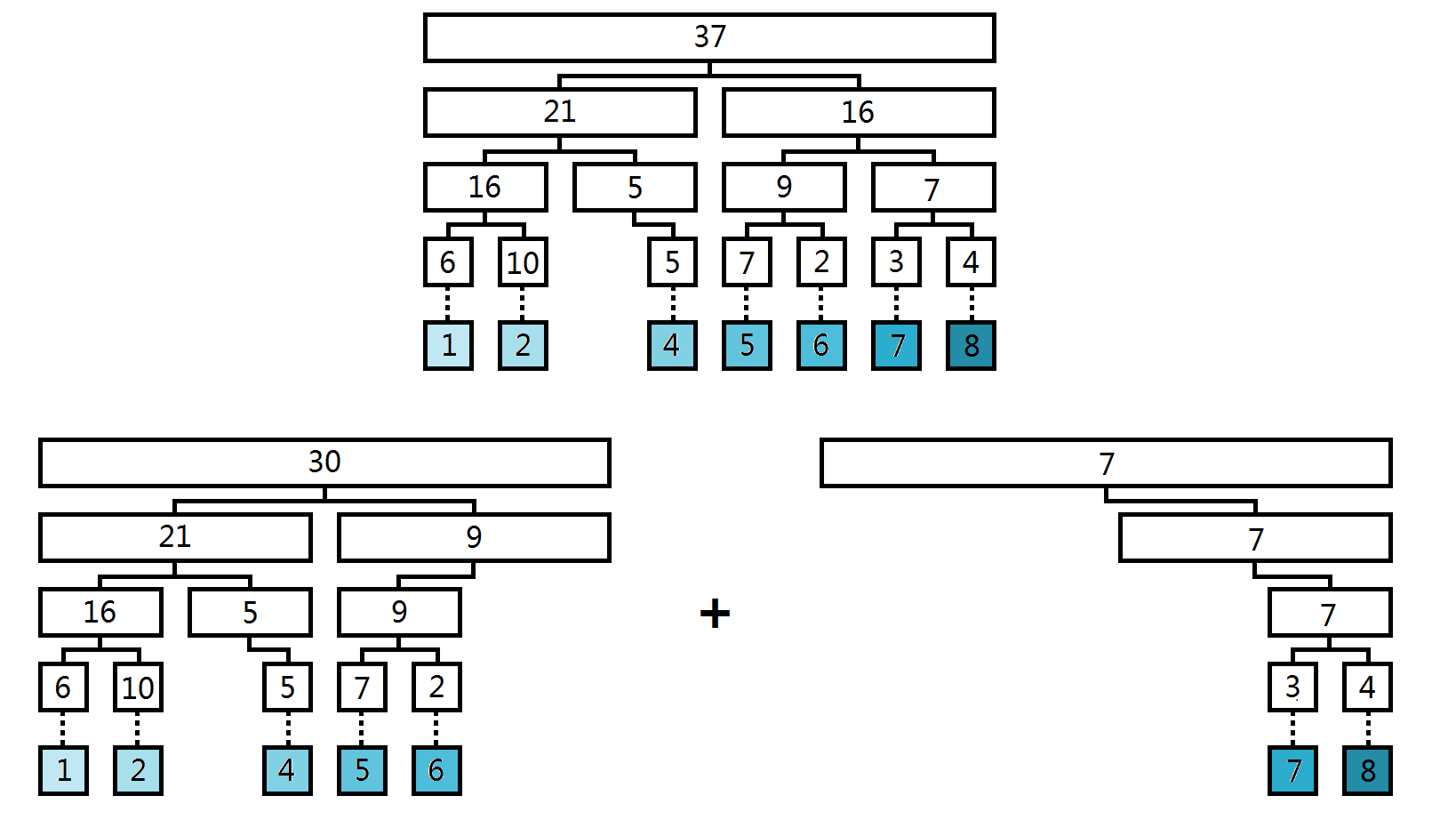
显而易见，线段树分裂就是合并的一个逆过程，通常是将值域由 \([l,r]\) 分裂成 \([l,x]\) 和 \([x+1,r]\) 两部分或是将前 \(k\) 小的元素与其他元素分成两部分（下面讲解前者，后者实现方法差不多）。

对于一个点（点设为 \(p\)，其左子树包含的值域最大值为 \(mid\)，原树记为 \(X\) 而分裂出来的新树记为 \(Y\)），考虑以下三种情况：

• 若 \(mid = x\)，那么将 \(p\) 的左子树留在 \(X\) 中，将右子树直接给 \(Y\)；

• 若 \(mid < x\)，那么左子树仍然保留在 \(X\)，递归右子树；

• 若 \(mid > x\)，那么右子树全部要给 \(Y\)，递归左子树。

例题

例 1 ： P5494 【模板】线段树分裂

题目大意

给定可重集 \(1\)（\(1\) 是编号），维护以下操作：

1. 将可重集 \(p\) 中值域在 \([x,y]\) 范围内的分离到一个新的可重集中（编号即为当前最大的可重集编号加一）；

2. 将可重集 \(t\) 并入可重集 \(p\) 中且保证之后的操作中不会出现 \(t\)；

3. 在可重集 \(p\) 中加入 \(x\) 个数字 \(q\)；

4. 查询可重集 \(p\) 中 \([x,y]\) 内的数字个数；

5. 查询可重集 \(p\) 中排名为 \(k\) 的数。

思路

显然开权值线段树维护即可。

• 对于操作 \(1\)，分裂出 \([x,y]\) 相当于是 \([1,n]\xrightarrow{split[1,n]}[1,x-1]\ [x,n]\xrightarrow{split[x,n]} [1,x-1]\ \ [x,y]\ \ [y+1,n]\xrightarrow{merge[1,x-1]\,[y+1,n]} [1,x-1]\cup[y+1,n]\ \ [x,y]\)。注意要特判 \(x=1\) 与 \(y=n\) 的情况；

• 对于操作 \(2\)，即为线段树合并；对于操作 \(3\)，即为单点修改；对于操作 \(4,5\)，即为基础查询。

#include<iostream>
#include<cstdio>
#define maxn 200005
#define maxp 4000005
#define ll long long
using namespace std;
int n,m,opt,x,y,z,dele[maxp],len=0; int root[maxn],tot=0,cnt=1; struct seg_tree{int l,r; ll ans;}a[maxp];
void del(int p){dele[++len]=p; a[p].l=a[p].r=a[p].ans=0;}
void push_up(int p){a[p].ans=a[a[p].l].ans+a[a[p].r].ans;}
void insert(int &p,int l,int r,int num,int ti){ // add number 'num' 'ti' times at node 'p'
	if(!p) p=(len>0?dele[len--]:++tot); if(l==r){a[p].ans+=ti; return;}
	if(num<=(l+r)/2) insert(a[p].l,l,(l+r)/2,num,ti); else insert(a[p].r,(l+r)/2+1,r,num,ti); push_up(p);
}
void split(int p,int &q,int l,int r,int num){ // split numbers not less than 'num' in node 'p' into a new node 'q'
	if(!q) q=(len>0?dele[len--]:++tot); if(num>(l+r)/2){split(a[p].r,a[q].r,(l+r)/2+1,r,num); push_up(p); push_up(q); return;}else swap(a[p].r,a[q].r);
	if(num<(l+r)/2) split(a[p].l,a[q].l,l,(l+r)/2,num); push_up(p); push_up(q); return;
}
int merge(int p1,int p2,int l,int r){ // merge the nodes 'p1' and 'p2' 
	if((!p1)||(!p2)) return p1+p2; if(l==r){a[p1].ans+=a[p2].ans; return p1;}
	a[p1].l=merge(a[p1].l,a[p2].l,l,(l+r)/2); a[p1].r=merge(a[p1].r,a[p2].r,(l+r)/2+1,r); push_up(p1); del(p2); return p1;
}
ll search(int p,int l,int r,int le,int ri){ // find the number of numbers greater than 'le' and less than 'ri' at node 'p' 
	if(le<=l&&ri>=r) return a[p].ans; ll res=0; if(le<=(l+r)/2) res+=search(a[p].l,l,(l+r)/2,le,ri);
	if(ri>(l+r)/2) res+=search(a[p].r,(l+r)/2+1,r,le,ri); return res;
}
int getrank(int p,int l,int r,int rnk){ // find the number of rank 'rnk' at node 'p' 
	if(rnk>a[p].ans) return -1; if(l==r) return l;
	if(rnk<=a[a[p].l].ans) return getrank(a[p].l,l,(l+r)/2,rnk); else return getrank(a[p].r,(l+r)/2+1,r,rnk-a[a[p].l].ans);
}
void cut(int x,int y,int z){ // split numbers greater than 'y' and less than 'z' in multiset 'x' into a new multiset 
	int tmp1=0,tmp2=0; if(y>1) split(root[x],tmp1,1,n,y-1); else{tmp1=root[x]; root[x]=0;}
	if(y<n) split(tmp1,tmp2,1,n,z); else tmp2=0; ++cnt; root[cnt]=merge(root[cnt],tmp1,1,n); root[x]=merge(root[x],tmp2,1,n);
}
int main(){
	scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){scanf("%d",&x); if(x!=0) insert(root[1],1,n,i,x);}
	while(m--){
		scanf("%d",&opt);
		if(opt==0){scanf("%d%d%d",&x,&y,&z); cut(x,y,z);}
		// split numbers greater than 'y' and less than 'z' in multiset 'x' into a new multiset 
		else if(opt==1){scanf("%d%d",&x,&y); root[x]=merge(root[x],root[y],1,n);} // merge multiset 'y' into multiset 'x' 
		else if(opt==2){scanf("%d%d%d",&x,&y,&z); insert(root[x],1,n,z,y);} // add number 'z' 'y' times at node 'x' 
		else if(opt==3){scanf("%d%d%d",&x,&y,&z); printf("%lld\n",search(root[x],1,n,y,z));}
		// find the number of numbers greater than 'y' and less than 'z' in multiset 'x' 
		else{scanf("%d%d",&x,&y); printf("%d\n",getrank(root[x],1,n,y));} // find the number of rank 'y' in multiset 'x' 
	}
	return 0;
}
/*
5 2
1 2 3 4 5
0 1 3 4
4 1 8
*/

例 2 ：