可持久化线段树

线段树

尽人皆知，线段树是一种能够在 \(\mathcal{O}(\log n)\) 时间内处理区间修改及查询（最基础）的数据结构。那么，当我们加上了「时间」这一维度后，应该如何处理呢？

可持久化线段树

简单地说，“可持久化”这一概念就是在每一个操作上打上了时间这一标记，在之后的某次操作中可以随时回溯至某一时刻或操作（类比编辑软件中的 Ctrl + Z 操作）。

最朴素的一种想法就是，对于每一个操作，我们都另外开一颗线段树来存储当前的状态，要回溯时直接回到那个时间戳对应的线段树进行接下来的操作即可。

但是，这样做的时空复杂度无疑是非常大的，如图，假设我们要对 \(x=8\) 进行单点修改操作，我们要修改的点应该是如下图蓝色部分：

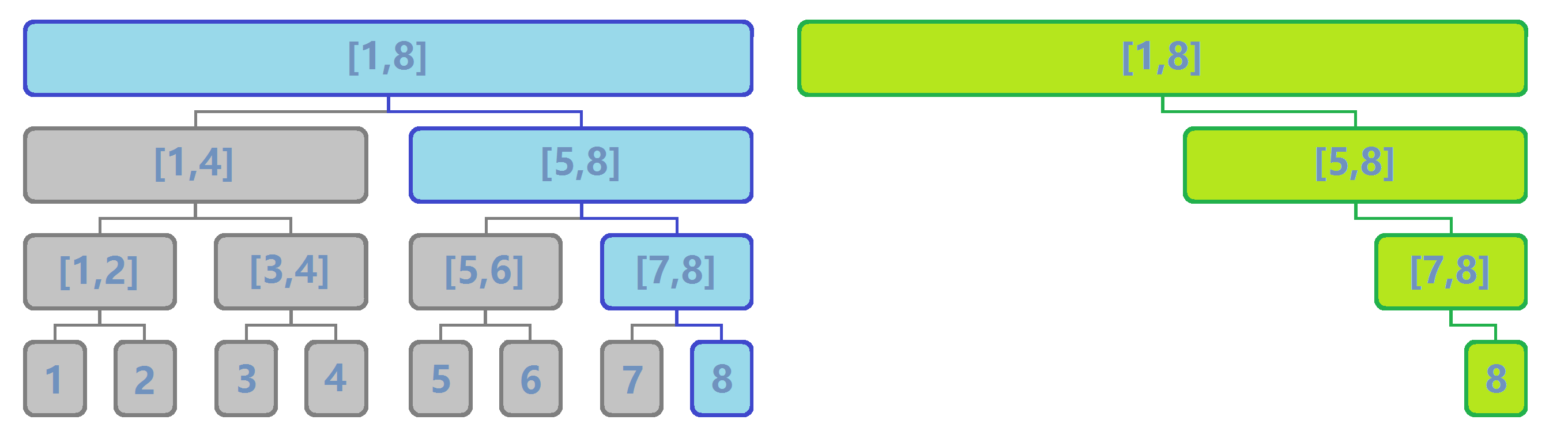
发现根本没有多少节点被修改，所以我们不妨只给这些修改过的点开新节点，而对于没有修改的子节点我们直接连边：

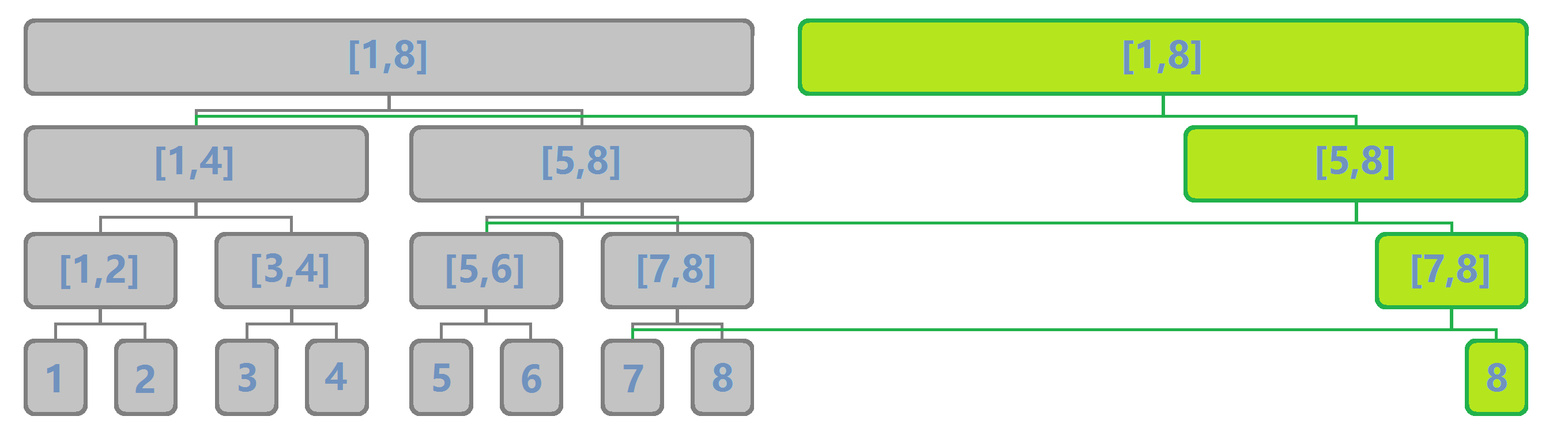
这就是可持久化线段树的精髓所在，我们为每一个时间的线段树存一个根：有修改就新建根，否则若是查询就指向对应的根。

模板 1（可持久化数组）：

#include<iostream>
#include<cstdio>
#define maxn 1000005
using namespace std;
int n,m,tot=0,v,opt,loc,val,ori[maxn],root[maxn]; struct node{int ls,rs,val;}a[maxn*25];
void build(int &p,int l,int r){
	p=++tot; if(l==r){a[p].val=ori[l]; return;}
	build(a[p].ls,l,(l+r)/2); build(a[p].rs,(l+r)/2+1,r);
}
void change(int &p,int ver,int l,int r,int pos,int val){
	p=++tot; a[p]=a[ver]; if(l==r&&l==pos){a[p].val=val; return;}
	if(pos<=(l+r)/2) change(a[p].ls,a[ver].ls,l,(l+r)/2,pos,val);
	else change(a[p].rs,a[ver].rs,(l+r)/2+1,r,pos,val);
}
int search(int ver,int l,int r,int pos){
	if(l==r&&l==pos) return a[ver].val;
	return ((pos<=(l+r)/2)?search(a[ver].ls,l,(l+r)/2,pos):search(a[ver].rs,(l+r)/2+1,r,pos));
}
int main(){
	scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%d",&ori[i]); build(root[0],1,n);
	for(int i=1;i<=m;i++){
		scanf("%d%d%d",&v,&opt,&loc);
		if(opt==1){scanf("%d",&val); change(root[i],root[v],1,n,loc,val);}
		else{root[i]=root[v]; printf("%d\n",search(root[v],1,n,loc));}
	}
	return 0;
}

模板 2（可持久化权值线段树）：

#include<iostream>
#include<cstdio>
#include<algorithm>
#define maxn 200005 
using namespace std;
int n,m,len,tot=0,le,ri,k,ori[maxn],uni[maxn],root[maxn]; struct node{int ls,rs,num;}a[maxn*25];
void build(int &p,int l,int r){
p=++tot; if(l==r) return; 
build(a[p].ls,l,(l+r)/2);build(a[p].rs,(l+r)/2+1,r);}
void add(int &p,int ver,int l,int r,int pos){
	p=++tot; a[p]=a[ver]; a[p].num++; if(l==r&&l==pos) return;
	if(pos<=(l+r)/2) add(a[p].ls,a[ver].ls,l,(l+r)/2,pos); else add(a[p].rs,a[ver].rs,(l+r)/2+1,r,pos);
}
int query(int v1,int v2,int l,int r,int rank){
	if(l>=r) return l;
	if(a[a[v2].ls].num-a[a[v1].ls].num>=rank) return query(a[v1].ls,a[v2].ls,l,(l+r)/2,rank);
	else return query(a[v1].rs,a[v2].rs,(l+r)/2+1,r,rank+a[a[v1].ls].num-a[a[v2].ls].num);
}
int main(){
	scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){scanf("%d",&ori[i]); uni[i]=ori[i];}
	sort(uni+1,uni+1+n); len=unique(uni+1,uni+1+n)-uni-1; build(root[0],1,n);
	for(int i=1;i<=n;i++){add(root[i],root[i-1],1,n,lower_bound(uni+1,uni+1+len,ori[i])-uni);}
	while(m--){scanf("%d%d%d",&le,&ri,&k); printf("%d\n",uni[query(root[le-1],root[ri],1,n,k)]);}
	return 0;
}