博弈论(例题)
例题
例 1 AGC017D/AT2667 Game on Tree
题目大意:有一棵有 \(n\) 个节点的树,节点编号依次为 \(1\sim n\),两人轮流进行以下操作:选择一条边将其断开将树分成两个联通块,舍去不含节点 \(1\) 的联通块。最先无法操作的一方输。问先手是否存在必胜策略(\(n\le 2\times 10^5\),时限 \(2s\))。
我们用一个节点的 SG 函数值表示以此节点为根的子树的 SG 函数值。
先给出结论:一个节点的 SG 函数值等于其子节点的 SG 函数值加 \(1\) 后的异或和。那么我们只需要对树 DFS 算出根的 SG 函数值即可。下面是结论的证明:
假设以节点 \(x\) 为根一棵子树有 \(k\) 个子节点,若 \(k > 2\),那么我们可以把节点 \(x\) 分成 \(k\) 个,每个对应一棵子树,由 SG 定理,整棵子树的 SG 应该是这 \(k\) 棵子树的 SG 值的异或和。
那么我们使用数学归纳法,假设 \(root\rightarrow son\rightarrow other\) 结构共有 \(t\) 个节点,下证 \(SG_{root} = SG_{son} + 1\)。
当 \(t = 2\) 时,显然 \(SG_{son} = 0,SG_{root} = 1\),满足条件。
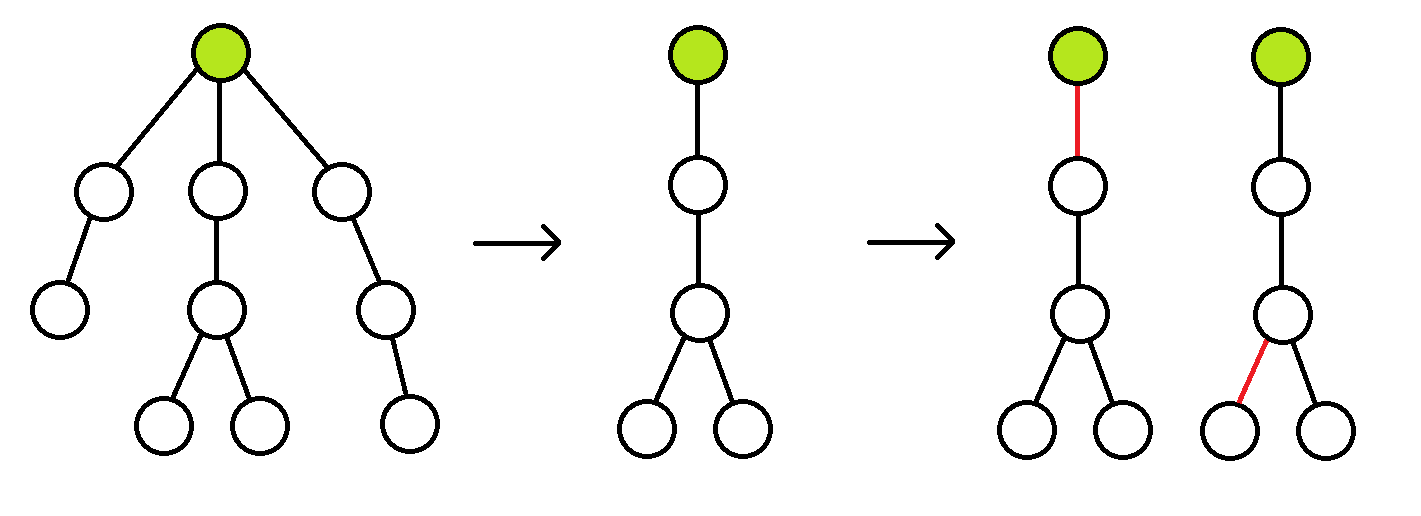
当 \(t\le i\) 都成立,\(t = i+1\) 时:对于其中的一棵子树,下一步操作有两种情况:
- 若断开了根与子节点的那条边,则剩下一个节点,SG 值显然为 0;
- 若断开了其它边,那么可以看做是在以根节点的子节点为根的子树中断开了一条边,而得到的所有的状态的 \(\operatorname{mex}\) 就是根节点的子节点的 SG 函数值,故一共能够得到的状态的 SG 值一定有 \(0\sim SG_{son[x]}-1\),而一定没有 \(SG_{son[x]}\),那么,根据假设,所有状态的 SG 应为 \(1\sim SG_{son[x]}\);
故根的 SG 值为它们的 \(\operatorname{mex}\),即 \(SG_{son} +1\),得证。
#include<iostream>
#include<cstdio>
#define maxn 100005
using namespace std;
int n,uu,vv; int sg[maxn]; struct node{int to,nex;}a[maxn*2]; int head[maxn],tot=0;
void add(int from,int to){a[++tot].to=to;a[tot].nex=head[from];head[from]=tot;}
int dfs(int p,int fa){ int res=0; for(int i=head[p];i;i=a[i].nex) if(a[i].to!=fa) res^=(dfs(a[i].to,p)+1); return res; }
int main(){
scanf("%d",&n); for(int i=1;i<n;i++){scanf("%d%d",&uu,&vv); add(uu,vv); add(vv,uu);}
if(dfs(1,-1)) printf("Alice"); else printf("Bob");
return 0;
}
例 2 ARC091F/AT3939 Strange Nim
题目大意:有 \(n\) 堆石子和长为 \(n\) 的数列 \(k\),第 \(i\) 堆有 \(a_i\) 个石子,两人轮流从这些石子中取走若干,要求每次只能从一堆中拿(假设拿了第 \(i\) 堆),拿的数量至少为 \(1\) 颗,最多不超过 \(\left\lfloor\dfrac{a_i}{k_i}\right\rfloor\) 颗(\(a_i\) 随石子数变化而动态变化),最先没有石子可取的一方输。问先手是否存在必胜策略(\(n\le 200,a_i,k_i\le 10^9\),时限 \(2s\))。
我们发现 \(n\) 堆石子间是独立的,所以我们把整个游戏分成 \(n\) 个子游戏来看,原游戏的 SG 就是所有子游戏的 SG 的异或和。问题就转化成了求一个子游戏的 SG 值。
同样地,我们 打表 算出不同石子数的 SG 值(以 \(k=8\) 为例)
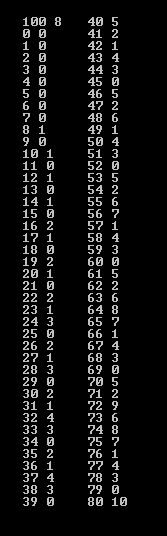
我们发现以下规律:
其实不难理解,\(SG(i) = \operatorname{mex}\{SG(i-x)\,|\,1\le x\le \left\lfloor\frac{i}{k}\right\rfloor\}\),当 \(\left\lfloor\frac{i}{k}\right\rfloor\) 不变时,SG 应该是一个循环节长度为 \(\left\lfloor\frac{i}{k}\right\rfloor+1\) 的长度为 \(k\) 的循环,且循环节恰好是 \(0\sim \frac{i}{k}\) 的一个排列。当 \(i\) 到 \(k\) 的倍数时(记为 \(i'\)),\(\left\lfloor\frac{i'}{k}\right\rfloor = \left\lfloor\frac{i}{k}\right\rfloor + 1\),取 \(\operatorname{mex}\) 的范围恰好覆盖了原来的一个循环节,故 SG 值应该为 \(\left\lfloor\frac{i}{k}\right\rfloor + 1 = \left\lfloor\frac{i'}{k}\right\rfloor\)。
根据这个规律,对于给定的一组 \(a\) 和 \(k\),我们一直将 \(a\leftarrow a-\left\lfloor\frac{a}{k}\right\rfloor-1\) 直到 \(a\) 为 \(k\) 的倍数。下面分析复杂度:\(a\leftarrow a-\left\lfloor\frac{a}{k}\right\rfloor-1\) 可以约等于是 \(a\leftarrow a\times\frac{k-1}{k}\),而 \((\frac{k-1}{k})^{k-1} = (\dfrac{1}{1+\frac{1}{k-1}})^{k-1} = \dfrac{1}{(1+\frac{1}{k-1})^{k-1}} \approx \frac{1}{e}\)(众所周知 \(\lim\limits_{x\to\infty}{(1+\frac{1}{x})^x} = e\)),故每 \((k-1)\) 次操作 \(a\leftarrow a\times\frac{1}{e}\)。总时间复杂度约为 \(\mathcal{O}(nk\ln a)\)。
显然会 TLE,考虑优化。类似于数论分块,\(\left\lfloor\frac{a}{k}\right\rfloor\) 在一定范围内是一个定值,所以我们把重复的 \(\left\lfloor\frac{a}{k}\right\rfloor\) 合并,大约是 \(\left\lceil\dfrac{a\bmod k}{\left\lfloor\frac{a}{k}\right\rfloor+1}\right\rceil\) 次。因为 \(\left\lfloor\frac{a}{k}\right\rfloor\) 在减少,所以最终的时间复杂度约在 \(\mathcal{O}\big(n \min(\dfrac{a}{k},k\ln a)\big) = \mathcal{O}(n\sqrt{a\ln a})\) 上下。
#include<iostream>
#include<cstdio>
#include<map>
#define maxn 100005
#define maxk 100005
using namespace std;
int n,a,k,ans=0;
int main(){
scanf("%d",&n);
for(int tt=1;tt<=n;tt++){
scanf("%d%d",&a,&k);
while(a>=k){
if(a%k==0){ans^=a/k;break;}
a-=(((a%k)/(a/k+1))+((a%k)%(a/k+1)!=0?1:0))*(a/k+1);
}
}
if(ans==0) printf("Aoki"); else printf("Takahashi");
return 0;
}
例 3 AGC010F/AT2307 Tree Game
题目大意:有一棵含 \(n\) 个节点的树,每个节点上有 \(a_i\) 颗石子。现在两人进行游戏,先手先将一个标记放在某个节点处,之后先后手轮流进行以下操作:取走有标记节点的一颗石子,然后沿边将标记移到下一个节点,最先没有石子可取者输。输出先手所有可以放标记且有必胜策略的点(\(2\le n\le 3000\),时限 \(2s\))。
记先手第一次放标记的点为根。
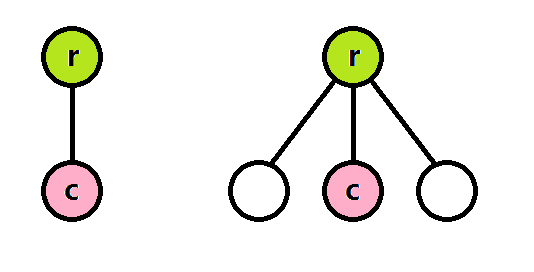
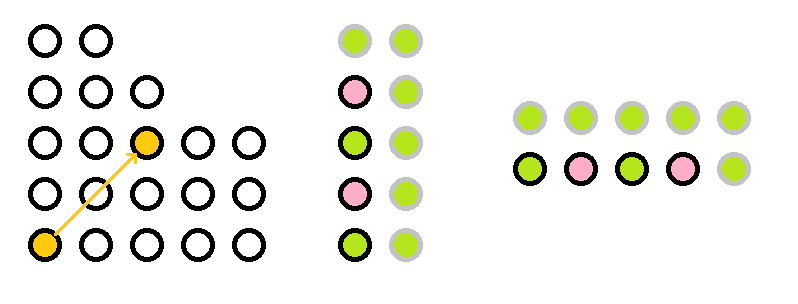
我们先来看一些简单的情况。如上左图,若只有两个点,显然只有 \(a_r > a_c\) 时才能赢,否则后手可以和先手反复横跳直至 \(a_r\) 先会等于 \(0\)。若根有多个子节点(假设子节点没有子树),一旦存在一个子节点 \(c\) 使得 \(a_r > a_c\),那么先手就能必胜。这是我们以下情况的基础。
我们先给出结论:当且仅当一个节点 \(v\) 存在一个子节点 \(c\) 满足 \(a_c < a_v\) 且以 \(c\) 为根的子树中先手必败(P - position),那么这个节点先手必胜(N - position),否则先手必败(P - position)。
下面给出证明:
若一个节点 \(v\) 满足上述条件,那么先手可以将标记移到子节点 \(c\) 上。之后,后手有两种方式:一是将标记移回 \(v\),那么先手可以再移回 \(c\),反复横跳直到 \(a_c\) 先为 \(0\),此时先手胜;二是往 \(c\) 的子树移,因为 \(c\) 是 P - position,所以先手也胜。即使后手先反复横跳几次使得 \(a_c\) 和 \(a_v\) 变小了,也不会改变 \(c\) 的状态(P - position)。
若一个节点 \(v\) 不满足上述条件:假设 \(v\) 的所有子节点都是 N - position,那么若把标记移过去后手一定必胜;假设 \(a_c \ge a_v\),那么由上面的基础情况,后手可以和先手反复横跳直到先手输。
所以,我们可以枚举根节点(第一次放标记的位置),进行 DFS 即可。复杂度 \(\mathcal{O}(n^2)\),可以过。
#include<iostream>
#include<cstdio>
#define maxn 3005
using namespace std;
int n,uu,vv,s[maxn]; struct node{int to,nex;}a[maxn*2]; int head[maxn],tot=0;
void add(int from,int to){a[++tot].to=to;a[tot].nex=head[from];head[from]=tot;}
int dfs(int p,int fa){
bool flag=0;
for(int i=head[p];i;i=a[i].nex)
if(a[i].to!=fa) if(!dfs(a[i].to,p)&&s[a[i].to]<s[p]) flag=1;return flag;
}
int main(){
scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&s[i]);
for(int i=1;i<n;i++){scanf("%d%d",&uu,&vv); add(uu,vv); add(vv,uu);}
for(int i=1;i<=n;i++) if(dfs(i,0)) printf("%d ",i);
return 0;
}
例 4 AGC002E/AT1999 Candy Piles
题目大意:有 \(n\) 堆糖果,两人轮流操作,每次操作可以拿走糖果个数最大的那一堆或每堆拿走一颗糖果,拿完糖果者输,求哪一方有必胜策略(\(1\le n\le 10^5\),时限 \(2s\))。
既然提到了最大值,不妨将糖果按数量从大至小排列,然后我们发现,两种操作的效果分别是去除最左边的一列和最下面的一行,可以看做是把糖果堆的左下角右移或上移的效果。而哪一方先将左下角移出边界就输了。
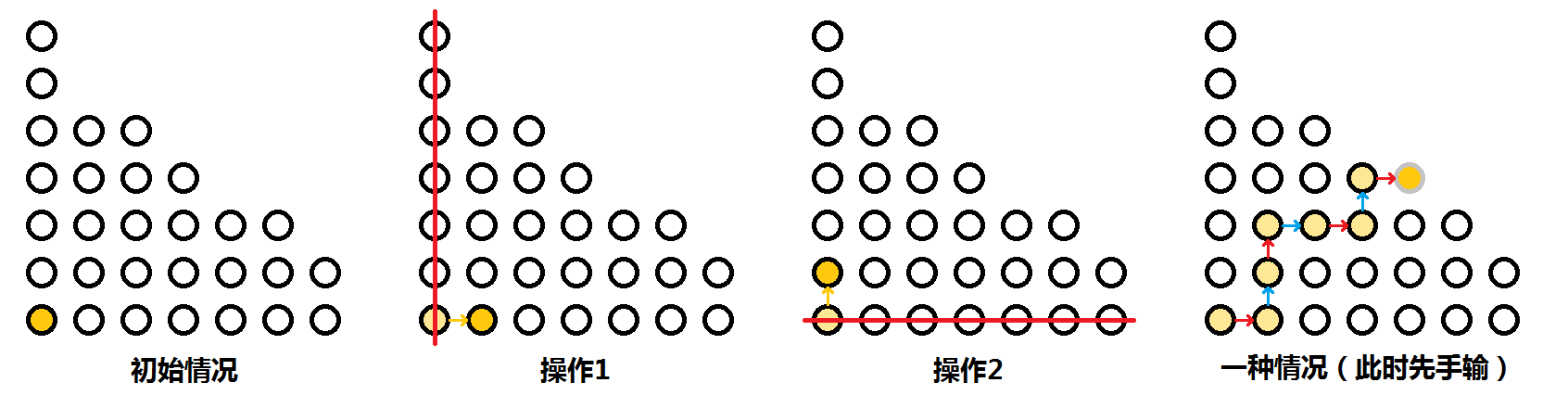
既然如此,我们考虑为每个点标上其为 P-position 或是 N-position(注意外面一圈边界是 N-position,因为超出边界说明上一个人拿走了最后一些,即上一方输了,先手必胜),如下图:
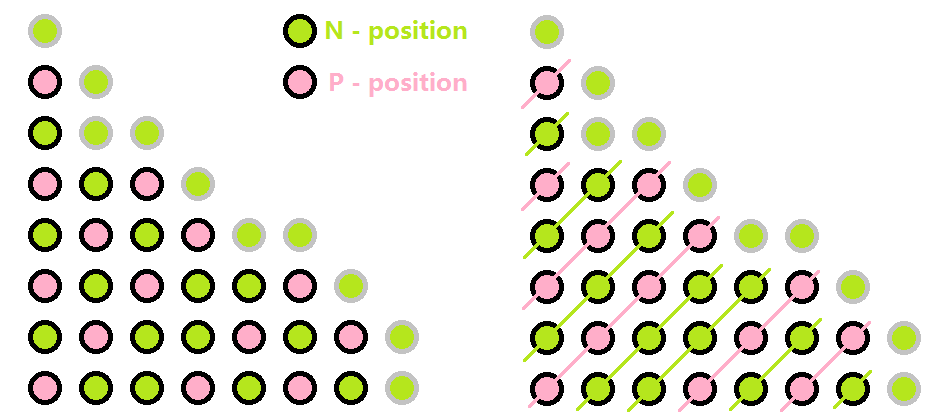
由图可知,每一条对角线上(除边界)的所有点的状态一样,不难证明:
- 若一个点是 P-position,故其下方和左方的点一定是 N-position,故其左下方的点也为 P-position;
- 若一个点是 N-position,其上方和右方的点至少有一个 P-position,不管哪一个是 P-position,其右上方的点都是 N-position。
所以,我们沿对角线可以找到与原状态 position 相同的最小状态,也就是向右上方搜直到恰好不超出边界即可。此时原图的状态就等于这个点的状态。我们发现此时这个点的状态与其离上方和右方最近的恰好处于边界上的点有关,因为其向上和向右时,点的状态交替改变。所以只要有奇数,原状态就是 N-position,否则为 P-position。
#include<iostream>
#include<cstdio>
#include<algorithm>
#define maxn 100005
using namespace std;
int n,a[maxn],m; bool cmp(int i,int j){return i>j;}
int main(){
scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]);
sort(a+1,a+1+n,cmp); for(int i=1;i<=n+1;i++) if(a[i]<i){m=i-1;break;}
for(int i=m+1;i<=n+1;i++) if(a[i]<m){printf("%s",((a[m]-m)%2|(i-m-1)%2)?"First":"Second"); break;}
return 0;
}
例 5 CF388C/CF388C Fox and Card Game
水题一道
题目大意:有 \(n\) 堆卡片,每堆有 \(a_i\) 张,每张卡片上有一个正整数 \(x\)。两人轮流取卡片,规定先手只能从某堆卡片的顶部取,后手只能从某堆卡片的底部取,求两人以最优策略最后能够得到的分数(拿到卡片上的数之和)(\(1\le n,a_i\le 100\),时限 \(1s\))。
显然,对于一堆卡片,双方都能够确保自己这一边的 \(\left\lfloor\frac{k}{2}\right\rfloor\) 张卡片不会被对方取走,因为对方那一端离这些卡比自己远,对方拿了你也拿就能确保拿到这些牌。
而实际上,双方都会拿走每堆牌中离自己较近的 \(\left\lfloor\frac{k}{2}\right\rfloor\) 张,因为如果对手一心想要拿你这边的牌,必然会空出自己的一些牌,若空出的牌比对手要抢的牌大的话,你就能得到更高的分数,显然对手采取最优策略的话不会这么干。那么,双方拿走离自己近的牌后,只有 \(k\bmod 2 = 1\) 的牌堆中会留下一张牌,因为它离双方一样近,所以双方会抢这些牌,一定是从大往小拿,放入大根堆维护即可。
#include<iostream>
#include<cstdio>
#include<queue>
#define maxn 105
using namespace std;
int n,ans1=0,ans2=0; int s,x; priority_queue<int> q;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d",&s);
for(int i=1;i<=s;i++){
scanf("%d",&x);
if(i<=s/2) ans1+=x; else if(s%2&&i==(s+1)/2) q.push(x); else ans2+=x;
}
}
bool flag=0;while(!q.empty()){if(!flag) ans1+=q.top();else ans2+=q.top();q.pop(); flag^=1;}
printf("%d %d",ans1,ans2);
return 0;
}
例 6 P8347 「Wdoi-6」另一侧的月
题目大意:有一棵有 \(n\) 个节点的树,两人轮流进行操作,每次操作可以断掉一条边并 选择 保留每个联通块。若某次操作结束后只剩下一个节点,则该操作的执行者输,求先手是否必胜(\(1\le \sum n\le 5\cdot10^5\),时限 \(1s\))。
首先分析最简单的状态:只有一个节点,显然这是一个 N - position(先手必胜,因为只有一个节点说明上一步只留下了一个节点,上一步操作者输了),而若是有两个节点相连即样例 3,则是 P - position(先手必败),这也是每种必败局面的最后一步(如果先手没有开摆的话)。
我们也可以思考一些特殊情况,如菊花图,当且仅当根有奇数个儿子时原图为 P - position,否则为 N - position,这其实我们思考原树节点的度奇偶性,我们发现:当且仅当所有节点的度数都为奇数时先手必败,否则先手必胜。利用 P - position 和 N - position 的定义我们可以加以证明。对于所有节点度数都是奇数的 P - position,我们断掉任意一条边 \(u\rightarrow v\) 都会使 \(u\) 和 \(v\) 的度数变成偶数,变成了 N - position;对于存在节点度数为偶数的 N - position,我们一定可以断掉连接某个度数为偶数的点的一条边使得某一个连通块中没有度数为偶数的点。
#include<iostream>
#include<cstdio>
#define maxn 100005
using namespace std;
int T,n,u,v,deg[maxn]; struct node{int to,nex;}a[maxn*2]; int head[maxn],cnt=0;
void add(int from,int to){a[++cnt].to=to; a[cnt].nex=head[from]; head[from]=cnt;}
void set(){for(int i=1;i<=n;i++){head[i]=deg[i]=0;} cnt=0;}
void dfs(int p,int fa){
for(int i=head[p];i;i=a[i].nex)
if(a[i].to!=fa){dfs(a[i].to,p); deg[p]+=deg[a[i].to];} deg[p]+=1;
}
int main(){
// freopen(".in","r",stdin); freopen(".out","w",stdout);
scanf("%d",&T);
while(T--){
set(); scanf("%d",&n);
for(int i=1;i<n;i++){scanf("%d%d",&u,&v); add(u,v); add(v,u);} dfs(1,0);
deg[1]--; bool ans=0; for(int i=1;i<=n;i++) ans|=(deg[i]&1^1);
if(ans) printf("Hifuu\n"); else printf("Luna\n");
}
return 0;
}
例 7 CF1149E/CF1149E Election Promises
题目大意:给定一张 \(n\) 个点 \(m\) 条边的有向图(不一定连通),每个点有一个权值 \(a_i\),两人轮流进行操作,每次操作可以选择任意一个节点 \(u\) 并将其点权 减小 为一个非负整数,之后可以将所有节点 \(v\in\{v|\,\exists\) 有向边 \(u\rightarrow v\}\) 的权值 更改 为任意非负整数,最先不能操作者输,求先手有无必胜策略,若有则接下来输出第一次操作后能够确保获胜的每个节点的权值(\(1\le n\le 2\times10^5\),\(0\le m\le 2\times10^5\),时限 \(2s\))。
我们发现这像一个 Nim 和有向图游戏的合成版,于是考虑计算 SG 值与 Nim 和。我们可以算出每一个点的 SG 值,令 \(f_x = \bigoplus\limits_{SG_p\ =\ x}a_p\),当且仅当 \(\forall x,f_x = 0\) 时先手必败,否则先手必胜,我们用 N - position 和 P - position 来证明。
对于任意一个 P - position,即 \(\forall x,f_x = 0\) 时,任意修改都会使得 \(\exists x,f_x\neq 0\),具体思路同 Nim 游戏。
对于任意一个 N - position,即 \(\exists x,f_x\neq 0\) 时,我们只需要找到最大的 \(x\) 使得 \(f_x\neq 0\),并找到一个 \(u\) 使得 \(SG_u = x,a_u\oplus f_x < a_u\)(参考 Nim 游戏的证明,一定存在这样的 \(u\)),将 \(a_u\leftarrow a_u\oplus f_x\),此时就将 \(f_x\) 清零了。而对于其它 \(f_y\neq 0(y < x)\),由于 SG 值由 mex 得到,\(u\) 的后继中一定存在 \(v\in\{v|\ SG_v = y,f_y\neq 0,y < x\}\),所以只要将 \(a_v\leftarrow a_v\oplus f_y\) 即可。
#include<iostream>
#include<cstdio>
#include<queue>
#include<map>
#define maxn 200005
#define ll long long
using namespace std;
int n,m,u,v,deg[maxn]; ll mmax,a[maxn],sg[maxn],xxor[maxn]; queue<int> q; map<int,int> mp[maxn];
struct node{int to,nex;}g[maxn],g2[maxn]; int head[maxn],head2[maxn],cnt=0,cnt2=0;
void add(int from,int to){g[++cnt].to=to; g[cnt].nex=head[from]; head[from]=cnt;}
void add2(int from,int to){g2[++cnt2].to=to; g2[cnt2].nex=head2[from]; head2[from]=cnt2;}
int main(){
scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
for(int i=1;i<=m;i++){scanf("%d%d",&u,&v); add(v,u); add2(u,v); deg[u]++;}
for(int i=1;i<=n;i++) if(deg[i]==0) q.push(i);
while(!q.empty()){
int top=q.front(); q.pop(); for(int i=0;;i++) if(!mp[top][i]){sg[top]=i; break;}
for(int i=head[top];i;i=g[i].nex)
{deg[g[i].to]--; mp[g[i].to][sg[top]]=1; if(!deg[g[i].to]) q.push(g[i].to);}
}
for(int i=1;i<=n;i++){xxor[sg[i]]^=a[i]; mmax=max(mmax,sg[i]);}
for(int i=mmax;i>=0;i--){
if(xxor[i]){
for(int j=1;j<=n;j++) if(sg[j]==i&&((a[j]^xxor[i])<a[j])){
a[j]^=xxor[i]; xxor[i]=0;
for(int k=head2[j];k;k=g2[k].nex) if(xxor[sg[g2[k].to]])
{a[g2[k].to]^=xxor[sg[g2[k].to]]; xxor[sg[g2[k].to]]=0;} break;
}
printf("WIN\n"); for(int i=1;i<=n;i++) printf("%lld ",a[i]); return 0;
}
if(i==0){printf("LOSE"); return 0;}
}
return 0;
}
例 8 CF1375F/CF1375F Integer Game
题目大意:有三堆石子,数量分别为 \(a,b,c\),现在两人博弈,进行以下操作:
- 先手选择一个整数 \(k\)(\(1\le k\le 10^{12}\));
- 后手选择一堆石子,将这对石子的数量增加 \(k\)。而且,后手不能选择上一次选择的那堆石子;
- 若某时刻有两堆石子数量一样先手胜,否则若进行了 \(1000\) 轮后先手都没有胜则后手胜。
告诉你 \(a,b,c\),请你选择先后手并吊打交互器(\(1\le a,b,c\le 10^9\),时限 \(1s\))。
我们思考在什么情况下先手能够胜,显然当 \(a,b,c\) 构成等差数列(不妨设 \(a<b<c\))且 \(c\) 不能被选时,先手能够选择公差 \(d\) 作为整数,此时后手不管选 \(a,b\) 哪一组都会使其中两堆石子相同。
下面考虑构造出等差数列。因为最大的一堆必须是上一次被选的,所以假设我们原来的石子是 \(a,b,c(a<b<c)\),那么当后手选 \(a\) 或 \(b\) 那一堆时,先手都可以取 \(k = 2*c-a-b\) 使得构成等差数列 \(b,c,2c-b\) 或 \(a,c,2c-a\),且最大的一堆不能被选。
所以我们只需要保证最大的一堆不能被选即可,显然先手可以取 \(k=10^{10}\) 等很大的数使得不管后手选哪组,那组都会变成最大的那一组从而输掉。所以该游戏先手有必胜策略能够在 \(3\) 回合内保证赢得游戏。
#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
ll a[4]; int x;
int main(){
scanf("%lld%lld%lld",&a[1],&a[2],&a[3]); printf("First\n10000000000\n"); fflush(stdout);
scanf("%d",&x); a[x]+=10000000000; swap(a[x],a[3]); printf("%lld\n",2*a[3]-a[1]-a[2]); fflush(stdout);
scanf("%d",&x); printf("%lld\n",a[3]-a[3^x]); fflush(stdout);
scanf("%d",&x); if(x==0) return 0; else{printf("The judger is BROKEN!"); fflush(stdout);}
return 0;
}
例 9 CF1503B/CF1503B 3-Coloring
有一个 \(n\times n\) 的棋盘和 \(3\) 种颜色,两人进行博弈,每一轮先手指定一种颜色,后手只能用另外的两种颜色的其中一种将一个格子染色。若两个相邻格子同色后手输,否则若 \(n\times n\) 轮结束所有格子都被染色且符合规则则先手输。作为后手吊打交互器(\(1\le n\le 100\),时限 \(3s\))。
显然除去一种颜色就剩两种颜色了,我们将棋盘按照奇偶黑白染色,用其中两种颜色尽量填,若其中一种颜色填满了就用剩下两种颜色填空缺处。
#include<iostream>
#include<cstdio>
#define ll long long
#define maxn 105
using namespace std;
int n,x; bool col[maxn][maxn],vis[maxn][maxn];
void op(bool pos,int col1,bool pos2,int col2){
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(!vis[i][j]&&col[i][j]==pos)
{vis[i][j]=1; printf("%d %d %d\n",col1,i,j); fflush(stdout); return;}
for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) if(!vis[i][j]&&col[i][j]==pos2)
{vis[i][j]=1; printf("%d %d %d\n",col2,i,j); fflush(stdout); return;}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){col[i][1]=col[i-1][1]^1; for(int j=2;j<=n;j++) col[i][j]=col[i][j-1]^1;}
for(int i=1;i<=n*n;i++){
scanf("%d",&x);
if(x==1) op(0,2,1,3); else if(x==2) op(1,1,0,3); else if(x==3) op(1,1,0,2);
}
return 0;
}
例 10 ARC151C/AT_arc151_C 01 Game
有 \(n\) 个格子,第 \(i\) 与 \(i+1\) 相邻。初始 \(m\) 个格子里有 0 或 1,两人轮流在没数字的格子里填 0 或 1,要保证相邻格子的数字不同,求谁赢(\(1\le n\le 10^{18}\),\(1\le m\le \min(n,2\times 10^5)\),时限 \(1s\))。
发现整个游戏被若干已存在的棋子分割成为若干个子游戏,考虑分别计算子游戏的 SG 值并计算异或和。
一个子游戏有且仅有四种情况,分别设 \(f_1(n),f_2(n),f_3(n),f_4(n)\) 表示长度为 \(n\) 的两端都没、一端有、两端相同和两端不同的子游戏,则(注意 \(f_3(0)\) 无意义):
打表:


得到:\(\begin{cases}f_1(n) = n\bmod 2\\f_2(n) = n\\f_3(n) = 1\\f_4(n) = 0\end{cases}\)。考虑用归纳法证明:显然 \(n = 0,1\) 时成立。假如 \(0\sim n-1\) 时均成立,那么:
- 对于 \(f_1(n) = \operatorname{mex}_{i=1}^n((i-1)\oplus(n-i))\):
在 \(n\) 为奇数时,存在 \(i = \dfrac{n+1}{2}\) 使得 \((i-1)\oplus(n-i) = \dfrac{n-1}{2}\oplus\dfrac{n-1}{2} = 0\),且不存在 \(i\) 使得 \((i-1)\oplus(n-i) = 1\)(假设存在,有 \(\begin{cases}(i-1) + (n-i) = n-1\\(i-1)\oplus(n-i) = 1\end{cases}\),得到 \(n-1\) 为奇数,矛盾),故此时 \(f_1(n) = 1\);
在 \(n\) 为偶数时,同理不存在 \(i\) 使得\((i-1)\oplus(n-i) = 0\)(假设存在,有 \(\begin{cases}(i-1) + (n-i) = n-1\\(i-1)\oplus(n-i) = 0\end{cases}\),得到 \(n-1\) 为偶数,矛盾),故此时 \(f_1(n) = 0\)。 - 对于 \(f_2(n) = \operatorname{mex}_{i=1}^n((i-1)\oplus 1,(i-1)\oplus 0)\):
后者刚好取遍 \(0\sim n-1\),又因为前者不可能等于 \(n\)(只有 \(n\) 为奇数且 \(i=n\) 时会等于,但是此时 \(f_3(n-i)\) 无意义),所以 \(f_2(n) = n\)。 - 对于 \(f_3(n) = \operatorname{mex}_{i=1}^n(1\oplus 1,0\oplus 0) = 1\);
- 对于 \(f_4(n) = \operatorname{mex}_{i=1}^n(1\oplus 0,0\oplus 1) = 0\)。
得证。
#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
ll n,m,pos,col,lascol,sgs;
int main(){
scanf("%lld%lld",&n,&m); if(m==0){if(n&1) printf("Takahashi"); else printf("Aoki"); return 0;}
for(int i=1;i<=m;i++){
scanf("%lld%lld",&pos,&col); if(i==1) sgs=pos-1; else sgs^=(col==lascol);
if(i==m) sgs^=n-pos; lascol=col;
} if(sgs==0) printf("Aoki"); else printf("Takahashi");
return 0;
}

