博弈论

简介

博弈论

博弈论，是经济学的一个分支，主要研究具有竞争或对抗性质的对象，在一定规则下产生的各种行为。博弈论考虑游戏中的个体的预测行为和实际行为，并研究它们的优化策略。
通俗地讲，博弈论主要研究的是：在一个游戏中，进行游戏的多位玩家的策略。 —— OI-wiki

而博弈论的题目通常有以下的特征：

• 两人轮流进行决策，且两人都使用最优策略；
• 能够在有限步后决出胜负；
• 两人的决策规则相同，公平竞争。

公平组合游戏 & 非公平组合游戏

公平组合游戏（Impartial Game）的定义是：

• 游戏由两人参与，轮流进行决策，且双方都知道游戏的全部信息；
• 任意一个游戏者在某一确定状态可以作出的决策集合只与当前的状态有关，而与游戏者无关；
• 游戏中的同一个状态不可能多次抵达，游戏以玩家无法进行合法的行动为结束，且游戏一定会在有限步后以非平局结束。

根据定义，传统的棋类游戏（如象棋等）都不算是公平组合游戏，因为不符合 “游戏者的决策集合只与当前状态有关而与游戏者无关” 一项（不能使用对方的棋子），它们是非公平组合游戏。

非公平组合游戏与公平组合游戏的最大区别就在于游戏者在某一确定状态可以做出的决策集合与游戏者有关。

P-position & N-position

P-position 的 P 代表 Previous，意为上一个做决策的人有必胜策略，即这个局面 先手必败；
N-position 的 N 代表 Next，意为下一个做决策的人有必胜策略，即这个局面 先手必胜。

严格的定义是：

• 没有后继（无法再移动）的局面（terminal position）是 P-position；
• 能够转移到 P-position 的局面是 N-position；
• 无法转移到 P-position（即所有决策都将转移到 N-position）的局面是 P-position。

博弈图

我们将游戏的每一个局面（状态）根据能否通过一步决策转移通过有向边相连，形成 DAG，这张图被称为博弈图。

例如，局面 \((3,4,2)\) 可以转移到 \((1,4,2)\)，在博弈图上表示为有有向边直接将它们相连，即有边：\((3,4,2)\rightarrow (1,4,2)\)。

有向图博弈与 Sprague-Grundy 函数 —— 以 Nim 游戏为例

有向图游戏

有向图游戏

有向图游戏是一个经典的博弈问题。

有向图游戏：在一张 DAG 中，某一个节点上有一颗棋子，两名玩家轮流将棋子沿有向边移动，最先不能移动的一方输。

有向图游戏的分析

如图为一个例子，根据我们刚才对于 P-position 和 N-position 的分析，我们可以对每一个节点进行判断其是先手必胜或先手必败。

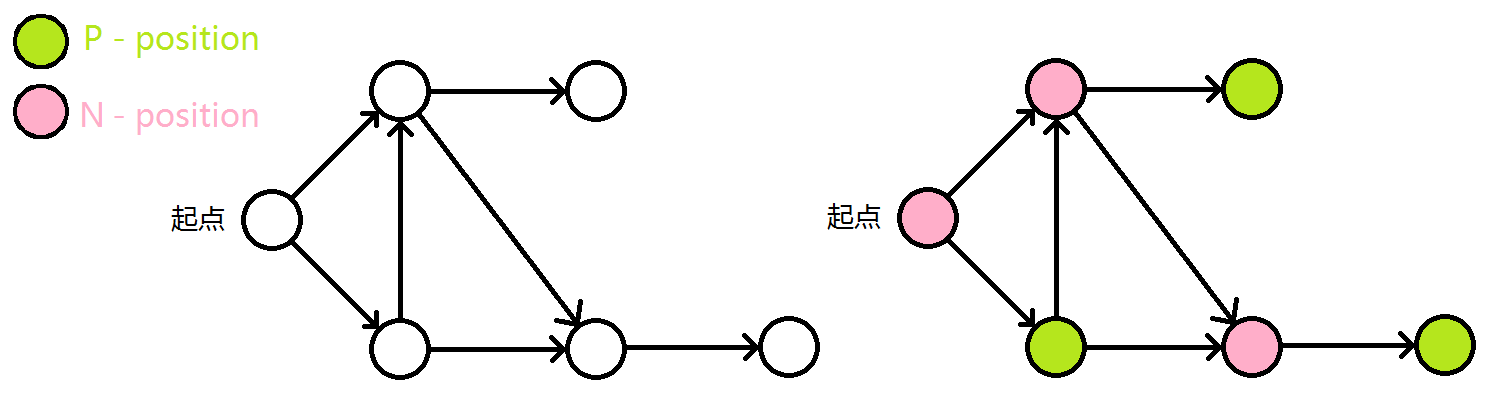
• 没有后继的局面是 P-position
  在有向图游戏中，唯一能够使游戏结束的方法就是将棋子移到不能再移的节点上，也就是说，所有出度为 \(0\) 的节点都是 P-position；
• 能转移到 P-position 的局面是 N-position；所有决策都转移到 N-position 的局面是 P-position
  根据这两条性质，我们可以将所有的节点确定下来。

可见原图是先手必胜的，最优策略就是每次向 P-position 的节点上移。

对于所有的有向图游戏，我们都可以这样分析，得到先手的获胜情况，复杂度是 \(\mathcal{O}(n)\) 的。

Nim 游戏

Nim 游戏

Nim 游戏是最经典的博弈论问题之一，得益于其简单的规则与优美的结论。

Nim 游戏：有 \(n\) 堆石子，每一堆分别有 \(a_i\) 个，两名玩家轮流从任意一堆石子中取出任意多个石子（不能不取），最先没有石子可取的一方输。
如，假设现在有三堆石子，分别为 \(3\) 个、\(4\) 个与 \(2\) 个，此时先手可以拿走第一堆中的 \(2\) 个（此时石子数变为 \(1、4、2\)）等等。

Nim 游戏的分析

记若干堆石子即它们所含石子个数为 \(n\) 元组 \((a_1,a_2,a_3,\dots,a_n)\)。

我们从最简单的情况下开始，假设只有一堆石子，显然这是 N-position，先手取走所有的石子就能获胜了。

如果有两堆石子呢？可以证明，只有当石子数不同时先手必胜。因为若两堆石子数相同时，先手拿走一堆的若干石子，后手可以选择另一堆拿走相同数量的石子，这样两堆石子数永远相等，直至先手取完一堆后后手取完另一堆，此时先手败。故两堆石子数相同的局面是 P-position。而若两堆石子数不相同，先手只需要拿走石子数多的那堆的若干石子，使得两堆石子数相同，就变成了一个 P-position，故先手必胜。

有三堆石子呢？此时的情况过于复杂，我们需要有更优的判断方法。

有向图游戏的转化

我们不妨画出 Nim 游戏的决策图。以 \((1,2)\) 这一初始局面为例，画出决策图如下：

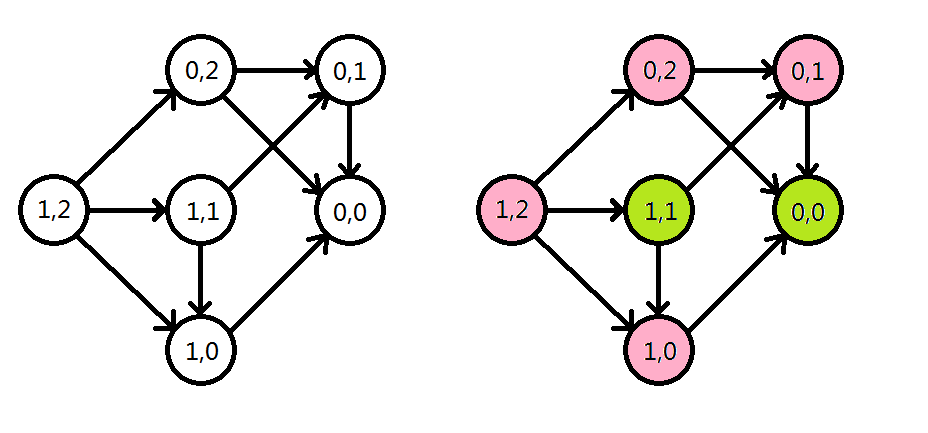
我们发现，每一方都能够将 Nim 游戏的一个状态通过状态图上的有向边转移到另一个状态，这恰好和有向图游戏一样。不仅如此，绝大部分的公平组合游戏都能通过博弈图转化为有向图游戏。

但是，此时想要求解，利用 DP 或是记忆化搜索都是 \(\mathcal{O}(\prod\limits_{i=1}^n{a_i})\) 的复杂度，所以我们要找一个更加快捷的方法。

Nim 和

暴力建图搜索或 DP 的复杂度太高了，于是我们想要找到更加快速的方法判断是否是 N-position 或 P-position。

我们定义 Nim 和为 \(\bigoplus\limits_{i=1}^n{a_i}\)（\(\oplus\) 为异或操作）。当且仅当 Nim 和为 0 时，该局面为 P-position，否则为 N-position。证明如下：

• 必败局面 \(a_i = 0\)，故 Nim 和显然为 0，满足 没有后继的局面是 P-position 的定义；
• 对于 \(\bigoplus_{i=1}^n{a_i}\neq0\) 的情况下，不妨设 \(\bigoplus_{i=1}^n{a_i} = k\)，且 \(k\) 的二进制最高位为第 \(j\) 位。我们只需要找到一个二进制最高位也为第 \(j\) 位的 \(a_i\)（一定存在，因为 \(k\) 的最高位一定由 \(a\) 中的奇数个最高位为 \(j\) 的数异或得到），将其变成 \(a_i' = a_i\oplus k\) 即可，因为 \(a_i\) 和 \(k\) 最高位都是 \(j\)，所以一定有 \(a_i' < a_i\)，是一步合法的操作，满足 能转移到 P-position 的局面是 N-position；
• 对于 \(\bigoplus_{i=1}^n{a_i} = 0\) 的情况下，假设存在一步操作将 \(a_i\) 变成 \(a_i'\) 后（\(a_i' < a_i\)）使得 \(a_1\oplus a_2\oplus a_3\oplus\dots\oplus a_i'\oplus\dots\oplus a_n = 0\)，将两式异或得到 \(a_i' = a_i\)，不符合假设，故满足 所有决策都转移到 N-position 的局面是 P-position。

所以，我们可以在 \(\mathcal{O}(n)\) 的时间内判断一个情况是 P-position 还是 N-position 了。

SG 函数

minimal excludant(mex)

首先引入 mex 函数的概念。

定义 mex 函数的值为不属于集合 S 中的最小非负整数，即 \(\operatorname{mex}(S) = \min{x}(x\notin S,x\in N)\)，例如 \(\operatorname{mex}(\{0,1,4,2\}) = 3，\operatorname{mex}(\{2,3,6\}) = 0，\operatorname{mex}(\varnothing) = 0\)。

SG 函数

对于一张 DAG，我们令每个节点 \(x\) 的 SG 函数 \(s(x) = \operatorname{mex}({s(y)\ |\ y}\) 是 \(x\) 的后继 \()\)。这样，我们可以为每个节点标上 SG 函数的值。

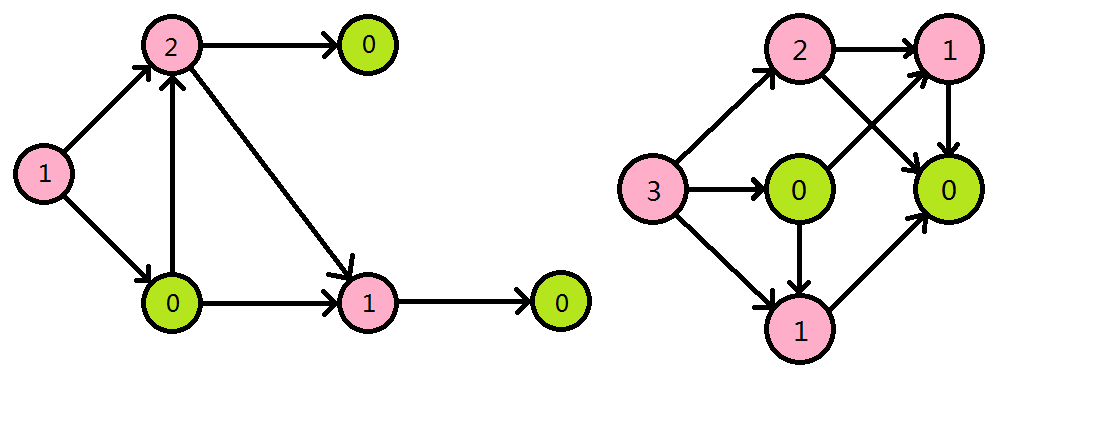
由图，SG 函数值为 \(0\) 的节点对应的状态就是 P-position，不为 \(0\) 的为 N-position，因为：

• 必败状态的 SG 函数值为 0（因为没有后继），满足 没有后继的局面是 P-position 的定义，所以是 P-position；
• 对于任意一个 SG 函数不为 \(0\) 的节点，其后继必定有 SG 函数值为 \(0\) 的节点；任意一个 SG 函数为 \(0\) 的节点，后继一定没有 SG 函数为 \(0\) 的节点，满足 能转移到 P-position 的局面是 N-position；无法转移到 P-position 的局面是 P-position。

那么，假设我们的游戏由多张 DAG 构成呢？

首先，我们考虑每个节点的 SG 函数值的意义。我们发现，对于 SG 函数值为 \(x\) 的节点（\(x > 0\)），其后继一定至少有 SG 函数值为 \(0\sim (s(x)-1)\) 的节点，先手可以任意选择到哪一个，这和 Nim 游戏恰好一样。所以，若有多张 DAG，我们就可以把它们看做 Nim 游戏的 \(n\) 堆石子，并使用 Nim 和求解。

所以，总的来说，一个由 \(n\) 个游戏组合成的一个游戏时，我们只需要找到这 \(n\) 个游戏对应的初始状态 SG 函数值，再将它们看做是 Nim 的石子堆，使用 Nim 和求解即可。

博弈论经典模型

Nim Game

不要问我为什么又有 Nim
由上，Nim 游戏的结论是：先手必败当且仅当所有堆的石子数异或和为 0。

阶梯 Nim

阶梯 Nim：阶梯 Nim 是 Nim 游戏的一个变种，其规则类似与 Nim 游戏。具体为：有 \(n\) 堆石子放置在一个有 \(0\sim n\) 层的阶梯的第 \(1\sim n\) 层（一层一堆），两名玩家轮流从 \(1\sim n\) 层中选择一层并将这一层的石子堆中的若干个（不能不拿）放到下一层，最先没有石子取的一方输。

阶梯 Nim 的必胜条件类似于 Nim：当且仅当奇数层上的石子个数的 Nim 和为 0 先手必败，否则先手必胜。

因为若一方移动偶数层上的石子，另一方就能再将这些石子再向下移一层使得 Nim 和不变。剩余证明过程类似 Nim。

Bash Game

Bash 博弈:有一堆石子，共 \(n\) 个，两人轮流取，每次可以取 \(1\sim m\) 块石子，最先没有石子可取的一方输。

以 \(n=6,m=3\) 为例画出博弈图与 SG 函数值。

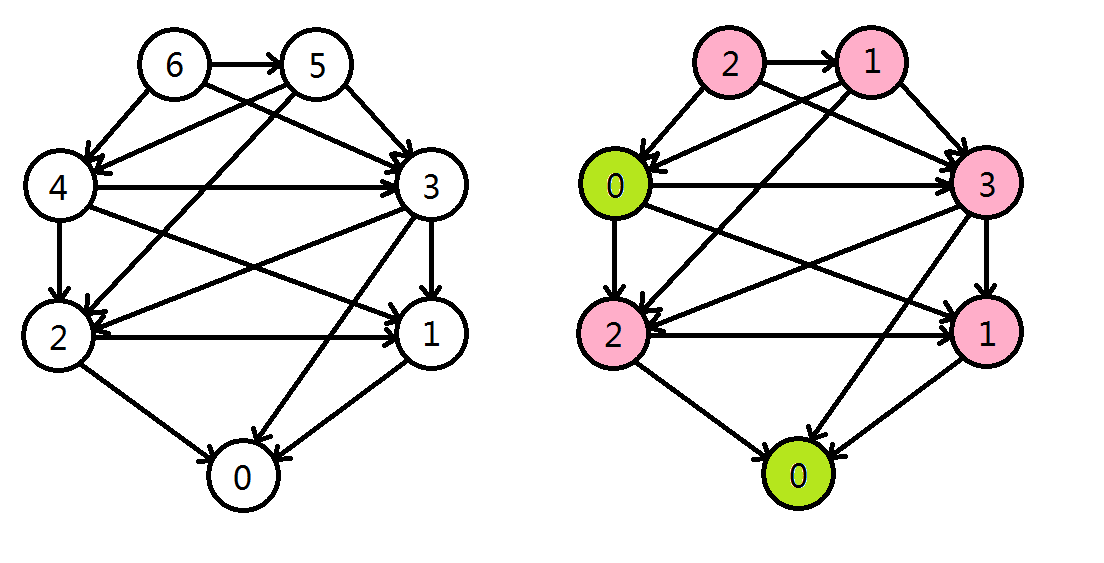
发现在图中，只有 \(0\) 和 \(4\) 两点是 P-position，更加一般地，当我们改变 \(n,m\) 时，得到所有的 P-position 如下：

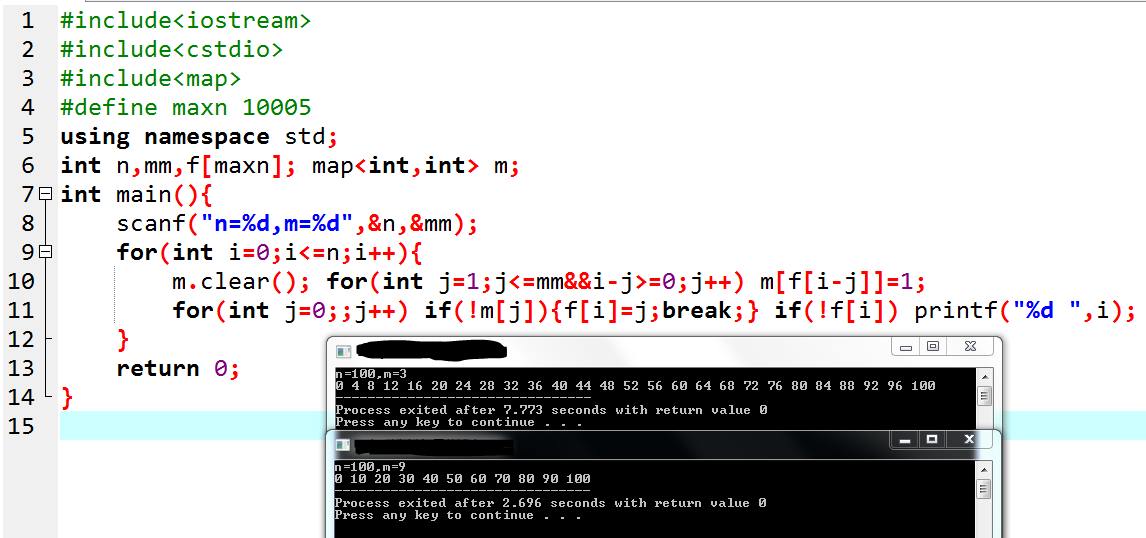
图中，当且仅当石子个数为 \((m+1)\) 的倍数时，局面才为 P-position，这不难证明：

• 必败状态的石子数为 \(0\)，满足是 \((m+1)\) 的倍数；
• 石子数不为 \((m+1)\) 的倍数时，只需要取走石子数模 \((m+1)\) 个石子就能将其变为 \((m+1)\) 的倍数；石子数为 \((m+1)\) 的倍数时，无论拿几颗石子数都不能变为 \((m+1)\) 的倍数。

综上，Bash 游戏的结论是：假设石子数 \(n \bmod (m+1) = r\)，当且仅当 \(r = 0\) 时先手必败，否则先手必胜。

Wythoff Game

Wythoff 博弈：有两堆石子，两人轮流取，每次可以在一堆里取任意多石子，或能从两堆中同时取出任意多相同数量的石子，最先没有石子可取的一方输。

博弈图不好画，直接上程序暴力计算 SG 函数并找出一些 P-position：

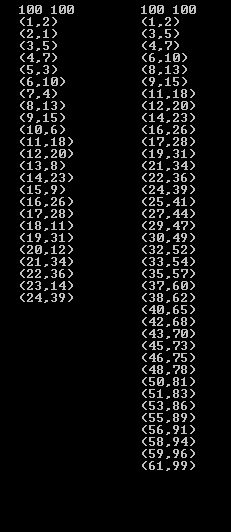
跑出来如左边那一列，我们发现有重复的如 \((1,2)\) 和 \((2,1)\)（两堆石子的顺序不影响有无必胜策略），去除后得到右边的一列。我们称这些局面为奇异局势（即 P-position）。

我们记石子数为二元组 \((a_i,b_i)\)，由图得出以下性质：

• 任一正整数都出现在了奇异局势的数中；
• \(a_i = \operatorname{mex}(a_0,b_0,a_1,b_1,a_2,b_2,\dots,a_{i-1},b_{i-1})\)；
• \(b_i = a_i + i\)。

这里给出奇异局势的判断方法：若 \(x = \left\lfloor\dfrac{\sqrt{5}+1}{2}(y-x)\right\rfloor\)，则 \((x,y)\) 为奇异局势。证明如下（百度百科：下面的过程可能需要比较高的数学技巧）。

P-position 判断的证明

Step 1

若 \((a,b)\) 为奇异局势，那么 \((b,a)\) 也为奇异局势，\((a+t,b),(a,b+t),(a+t,b+t)(t\in Z\) 且 \(a+t\ge 0,b+t\ge 0)\) 均不为奇异局势。

显然成立。以下将这两种看作一种局势。

Step 2

所有的奇异局势中，每个正整数恰好都出现且仅出现一次。

反证法：

• 假设有一个正整数 \(k\) 在奇异局势中出现了两次，假设若为 \((k,a)\) 和 \((k,b)\)，它们都是奇异局势，与 Step 1 矛盾；
• 假设有一个正整数 \(k\) 未在奇异局势中出现，则 \((k,k+t)(t\in N^*)\) 必不为奇异局面，则对于任意 \(t\)，必然存在 \(s(s\in N^*,0 < s < k)\) 使得 \((k,k+t-s)、(k-s,k+t)、(k-s,k+t-s)\) 其中之一为奇异局势（能转移到 P-position 的局面是 N-position），又因为 \((k,k+t-s)\) 不为奇异局势，故 \((k-s,k+t)、(k-s,k+t-s)\) 必有一个为奇异局势。
  根据抽屉原理，\(t\) 的取值有无穷种，而 \(s\) 只有有限（\(k-1\)）种取值，必然存在三个 \(t_1,t_2,t_3\)，使得 \(s_1 = s_2 = s_3\)。又根据抽屉原理，其中必有两个 \(t_x,t_y\) 使得 \((k-s_1,k+t_x)\) 和 \((k-s_1,k+t_y)\) 或 \((k-s_1,k+t_x-s_1)\) 和 \((k-s_1,k+t_y-s_1)\) 两组之一同时为奇异局势，与 Step 1 矛盾。

故每个正整数恰好都出现且仅出现一次。

Step 3

\(a_i = \operatorname{mex}(a_0,b_0,a_1,b_1,a_2,b_2,\dots,a_{i-1},b_{i-1})\)

根据 Step 2，每个正整数都出现且恰好一次，根据我们的排序方式，\(a_i>a_{i-1},b_i>a_i\)，故 \(a_x(x > i)\) 与 \(b_x(x\ge i)\) 都大于 \(a_i\)，那么 \(a_i\) 只能等于 \(a_i = \operatorname{mex}(a_0,b_0,a_1,b_1,a_2,b_2,\dots,a_{i-1},b_{i-1})\)，否则这个数不会出现，与 Step 2 矛盾。

Step 4

\(b_i = a_i + i\)

采用归纳法证明：

• 当 \(i=0\) 时，\(a_i = b_i = 0\)，显然成立。

• 当前 \(p\) 个奇异局势均为 \((a_i,a_i + i)(0\le i\le p)\)，下证，第 \((p+1)\) 个奇异局势是 \((a_{p+1},a_{p+1}+p+1)\)：
  由 所有决策都转移到 N-position 的局面是 P-position，我们只需要证明 \((a_{p+1}-t,a_{p+1}+p+1)、(a_{p+1},a_{p+1}+p+1-t)、(a_{p+1}-t,a_{p+1}+p+1-t)(0 < t < a_{p+1})\) 均不为奇异局势即可：

• \((a_{p+1}-t,a_{p+1}+p+1)\)：由 Step 2 与 Step 3，\(1\sim a_{p+1}-1\) 都在之前的奇迹局势中出现过，假设 \(a_{p+1}-t = a_x(x \le p)\)，则 \(b_x = a_x + x < a_{p+1} + p + 1\)，由 Step 1，一定不为奇异局势；

• \((a_{p+1},a_{p+1}+p+1-t)\)：分两种情况。
  若 \(a_{p+1}+p+1-t \ge a_{p+1}\)，那么我们可以从两堆都取走一些使其变成 \((a_{p+1-t},a_{p+1-t}+p+1-t)\) 这一奇异局势，由 能转移到 P-position 的局面是 N-position，该局面一定不是奇异局面；
  若 \(a_{p+1}+p+1-t < a_{p+1}\)，那么该局面就是 \((a_{p+1}+p+1-t,a_{p+1})\)，由 Step 2 和 Step 3，一定有 \(a_{p+1}+p+1-t = a_x(x \le p)\)，则 \(b_x = a_x + x < a_{p+1}\)，由 Step 1，一定不为奇异局势；

• \((a_{p+1}-t,a_{p+1}+p+1-t)\)：由 Step 2 和 Step 3，一定存在 \(a_{p+1}-t = a_x(x \le p)\)，则 \(b_x = a_x + x < a_{p+1}+p+1-t\)，由 Step 1，一定不为奇异局势。

Lemma 1：Beatty Theorem

Beatty 定理：若 \(a,b\) 是正无理数且满足 \(\frac{1}{a} + \frac{1}{b} = 1\)，记 \(P = \left\{\,\left\lfloor na\right\rfloor\ |\ n\in Z^*\right\}，Q = \left\{\,\left\lfloor nb\right\rfloor\ |\ n\in Z^*\right\}\)，则有 \(P\cap Q = \varnothing,P\cup Q = N^*\)

其中记正无理数 \(\alpha\) 和 \(\beta\)，满足 \(\frac{1}{\alpha} + \frac{1}{\beta} = 1\)，构造数列 \(a_n = \left\lfloor n\alpha\right\rfloor\)，\(b_n = \left\lfloor n\beta\right\rfloor\)，这两个数列被称为 Beatty 数列。

接下来我们采用反证法证明 Beatty 定理。

首先证明 \(P\cap Q = \varnothing\)：
假设 \(P\cap Q \neq \varnothing\)，不妨设 \(k\in P\cap Q\)，即 \(\exist\ m,n\in Z^*,k = \left\lfloor ma\right\rfloor = \left\lfloor nb\right\rfloor\)。
得到 \(k < ma < k+1,k < nb < k+1\)，所以 \(\dfrac{m}{k+1} < \dfrac{1}{a} < \dfrac{m}{k},\dfrac{n}{k+1} < \dfrac{1}{b} < \dfrac{n}{k}\)。
两式相加得到 \(\dfrac{m+n}{k+1} < 1 < \dfrac{m+n}{k}\)，即 \(k < m+n < k+1\)，与 \(k,m,n\in Z^*\) 矛盾，故假设不成立，原命题为真。

接下来证明 \(P\cup Q = N^*\)：
显然 \(P\cup Q \subseteq N^*\)，只需证明 \(N^* \subseteq P\cup Q\) 即可。
假设 \(N^*\) 不是 \(P\cup Q\) 的子集，假设 \(\exist\ k\in N^*,k\notin P\cup Q\)，即 \(\exist\ m,n\in Z^*\)，使得 \(\left\lfloor ma\right\rfloor < k < \left\lfloor (m+1)a\right\rfloor,\left\lfloor nb\right\rfloor < k < \left\lfloor (n+1)b\right\rfloor\)。
得到 \(ma < k \le\left\lfloor (m+1)a\right\rfloor - 1 < (m+1)a - 1,nb< k \le\left\lfloor (n+1)b\right\rfloor - 1 < (n+1)b - 1\)。
所以 \(\dfrac{m}{k} < \dfrac{1}{a} < \dfrac{m+1}{k+1},\dfrac{n}{k} < \dfrac{1}{b} < \dfrac{n+1}{k+1}\)。
两式相加得到 \(\dfrac{m+n}{k} < 1 < \dfrac{m+n+2}{k+1}\)，即 \(m+n < k < k+1 < m+n+2\)，与 \(k,m,n\in Z^*\) 矛盾，故假设不成立，原命题为真。

Step 5

由 Beatty 定理，Beatty 数列的两个数列都单调递增且每个正整数都出现且仅出现一次。

单调递增显然，下面证明每个正整数出现且仅出现一次：

设数列 \(a_n\) 的前 \(p\) 项小于等于 \(k\)（而从第 \((p+1)\) 项起大于 \(k\)），则有 \(\begin{cases}p\alpha < k+1\\(p+1)\alpha > k+1\end{cases}\)，故解得 \(\frac{k+1}{\alpha} - 1 < p < \frac{k+1}{\alpha}\)，即 \(p = \left\lfloor\frac{k+1}{\alpha}\right\rfloor\)。在 \(b_n\) 中同理。

故在两个数列中小于等于 \(k\) 的项一共有 \(S = \left\lfloor\frac{k+1}{\alpha}\right\rfloor + \left\lfloor\frac{k+1}{\beta}\right\rfloor\) 个。故 \((\frac{k+1}{\alpha}-1) + (\frac{k+1}{\beta}-1) < S < \frac{k+1}{\alpha} + \frac{k+1}{\beta}\)。又有 \(\frac{1}{\alpha} + \frac{1}{\beta} = 1\)，故 \(k-1 < S < k+1\)，即 \(S = k\)。

故两数列中，对任意 \(k\)，小于等于 \(k\) 的数有且仅有 \(k\) 个。每个正整数出现且仅出现一次成立。

Step 6(Final Step)

我们发现，奇异局势的 \((a_i,b_i)\) 变化规律和性质与 Beatty 序列的变化规律和性质十分相似，我们猜想奇异局势的 \(a_i,b_i\) 恰为 Beatty 序列。

令 \(b_p = a_p + p\)，代入得到 \(\left\lfloor p\alpha\right\rfloor + p = \left\lfloor p\alpha + p\right\rfloor = \left\lfloor p(\alpha + 1)\right\rfloor = \left\lfloor p\beta \right\rfloor\)，故 \(\beta = \alpha + 1\)。

代入原式得到 \(\frac{1}{\alpha} + \frac{1}{\alpha + 1} = 1\)，解得 \(\alpha = \dfrac{1\pm\sqrt{5}}{2}\)，舍负根得到 \(\alpha = \dfrac{1 + \sqrt{5}}{2}\)。

故 \(a_i = \left\lfloor \frac{1+\sqrt{5}}{2} i\right\rfloor,b_i = a_i + i\)，所以有 \(a_i = \left\lfloor \frac{1+\sqrt{5}}{2}(b_i - a_i)\right\rfloor\)。这就是判断是否是奇异局势的标准。

综上，Wythoff 游戏的结论是：若两堆石子数为 \(x,y\)，当且仅当 \(x = \left\lfloor \frac{1+\sqrt{5}}{2}(y - x)\right\rfloor(x\le y)\) 时先手必败，否则先手必胜。

Fibonacci Game

Fibonacci 博弈：有一堆石子，两人轮流取，先手先可以取任意多石子（不能取完），之后每一次取的石子数不能超过上一次的两倍，最先没有石子可取的一方输。

看名字就知道，结论肯定和斐波那契离不开关系。该游戏在石子数是斐波那契数是先手必败，否则先手必胜。证明如下。

P-position 判断的证明

记斐波那契数列为 \(f_1=0,f_2=1,\dots,f_i = f_{i-2} + f_{i-1}\)。

Lemma 1：Zeckendorf theorem

任一正整数 \(n\) 都能够分解成若干不连续的斐波那契数之和。

我们采用数学归纳法证明 Zeckendorf 定理：

• 当 \(n = 1,2,3\) 时，\(1 = f_1,2 = f_2,3 = f_3\)，显然成立；
• 当 \(n < m\) 时都成立，下证 \(n = m\) 时也成立：
  若 \(m\) 是斐波那契数，显然成立；
  若 \(m\) 不是斐波那契数，设 \(f_{x_0} < m < f_{x_0 + 1}\)，根据假设 \(m - f_{x_0} < m\) 能分解成不连续的斐波那契数之和（不妨设 \(m - f_{x_0} = f_{x_1} + f_{x_2} +\cdots + f_{x_t}\)，\(x_1 > x_2 > \cdots > x_t\) 且为不连续的正整数）。又因为 \(m - f_{x_0} < f_{x_0 + 1} - f_{x_0} = f _{x_0 - 1}\)，所以 \(f_{x_1} < m - f_{x_0} < f_{x_0 - 1}\)，即 \(x_0\) 与 \(x_1\) 也不连续。所以 \(n = m\) 也能够拆成若干不连续的斐波那契数之和。

Step 1

\(f_{n+1} < 2*f_n < f_{n+2}\)
\(f_{n+2} < 3*f_n\)
\(4*f_n < 3*f_{n+1}\)

对于第一条：\(f_{n+1} = f_n + f_{n-1} < 2*f_n\)，\(f_{n+2} = f_n + f_{n+1} > 2*f_n\)
对于第二条：\(f_{n+2} = f_n + f_{n+1} = 2*f_n + f_{n-1} < 3*f_n\)
对于第三条：\(4*f_n < 3*f_{n+1} \Leftrightarrow f_n < 3*f_{n-1}\)

Step 2.1(Final Step)

首先证明斐波那契数为 P-position。

采用数学归纳法证明：
记石子数 \(n = f_i\)。

• 当 \(i=3\) 时（\(i = 1\) 或 \(i = 2\) 时只有一颗石子，无法进行游戏），只有两颗石子，先手只能拿一颗，后手拿走第二颗，先手败。
• 当所有 \(i\le k\) 均成立时：
  则当 \(i = k+1\) 时，\(n=f_{k+1} = f_k + f_{k-1}\)，此时可以把石子看成 \(f_k\) 和 \(f_{k-1}\) 两堆。
  先手取时，一定不会取大于等于 \(f_{k-1}\) 颗，否则由于 Step 1 第二条，\(f_k < 3*f_{k-1}\)，后手能全部取完，先手就输了。故先手一定取小于 \(f_{k-1}\) 颗，由于 \(i\le k\) 时先手必败，故后手能够取完 \(f_{k-1}\) 这堆。
  我们再分析后手取完 \(f_{k-1}\) 那堆时最后一步取的石子数。假设先手第一次取了 \(p\) 颗，后手取完 \(f_{k-1}\) 堆时取了 \(q\) 颗。
  若 \(p\ge \dfrac{f_{k-1}}{3}\) 颗，由于 Step 1 第一条，后者一次就能全部取完，此时 \(q = f_{k-1} - p\le \dfrac{2*f_{k-1}}{3}\)。又由于 Step 1 第三条，\(4*f_{k-1} < 3*f_k\)，即 \(q = \dfrac{2*f_{k-1}}{3} < \dfrac{f_k}{2}\)，先手无法一次取完 \(f_k\) 那堆，由于 \(i\le k\) 时先手必败，后手胜。
  若 \(p < \dfrac{f_{k-1}}{3}\) 颗，此时 \(2p < \dfrac{2*f_{k-1}}{3}\)，同上，无论如何 \(q\) 总小于等于 \(\dfrac{2*f_{k-1}}{3}\)，故先手无法一次取完 \(f_k\) 堆，先手必败。

Step 2.2(Final Step)

接下来证非斐波那契数为 N-position。

根据 Zeckendorf 定理，我们可以将石子数分解为不连续的斐波那契数之和，即 \(n = f_{p_1} + f_{p_2} + \dots + f_{p_k}(p_1 < p_2 < \dots p_k\) 且 \(p_1\sim p_k\) 任意两个不连续 \()\)。

此时先手可以取走 \(f_{p_1}\) 颗，因为 \(p_2\ge p_1+2\)，所以根据 Step 1 第一条有 \(2*f_{p_1} < f_{p_2}\)，故先手不能一次拿完 \(f_{p_2}\) 堆。又由于其为 P-position，故先手能够拿完最后一颗，且根据 Step 2.1，最后一次拿的石子数 \(q < \dfrac{f_{3}}{2}\)，先手还能拿走 \(f_{3}\) 的最后一颗……如此下去，先手一定能够拿走 \(f_{p_k}\) 堆（最后一堆）的最后一颗石子。

综上，Fibonacci 游戏的结论是：当且仅当石子数为斐波那契数时先手必败，否则先手必胜。

例题

这篇的 Markdown 和 LaTeX 都快炸了
例题篇