CodeForces 1689C 题解

原题

大意

有一棵以 \(1\) 为根、有 \(n\) 个节点的二叉树。树根现在遭受了感染，在之后的每一秒钟，你能够去除树的一个节点，之后感染的节点向未感染的相邻节点传染。求能够保住的节点数的最大值（显然去除的节点不算保住）。

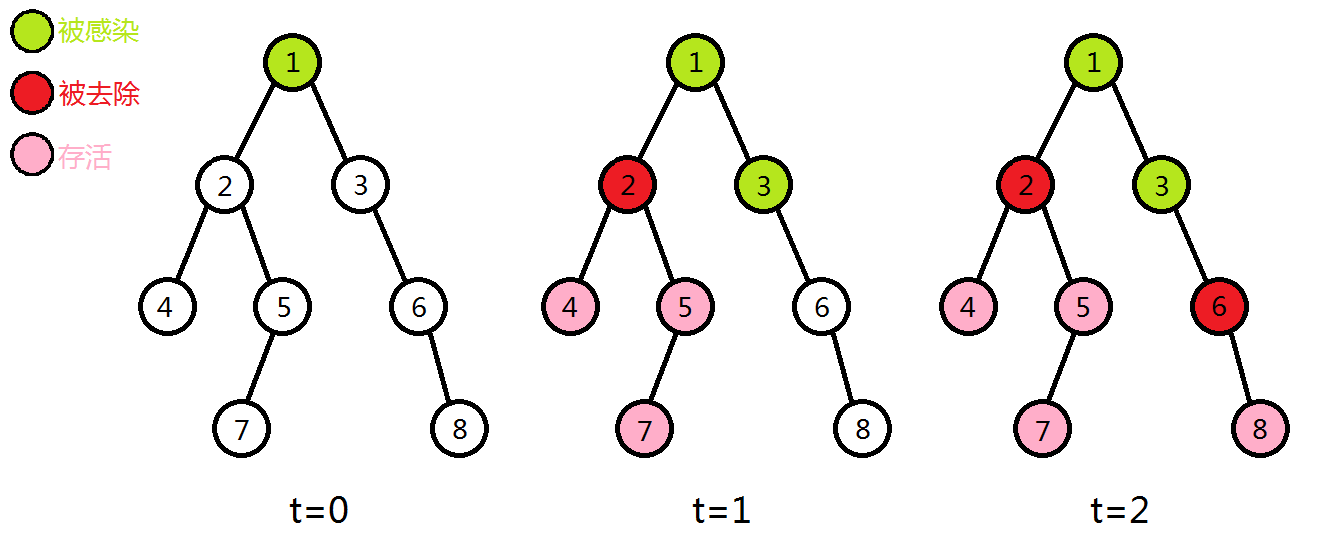
思路

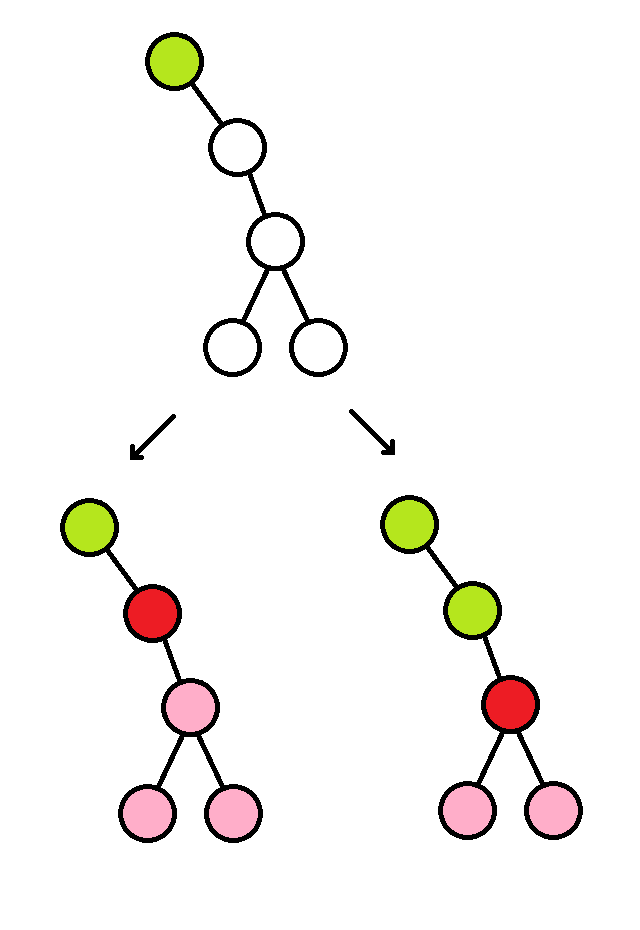
如图，当一个节点被感染时，我们若想去除其某棵子树里的点时，一定是去除与其直接相连的点更优。因为去除发生在感染之前，若去除不直接相连的点会让直接相连的点被感染，多损失了一个点。

之后，我们考虑到使用树形 DP 求解。令 \(f_i\) 为 \(i\) 被感染时，以 \(i\) 为根的子树中最多能够保住多少个点。答案就是 \(f_1\)。

接下来是转移方程：

因为是二叉树，那么一个点被感染后，接下来去除的点一定是其左右儿子 \(son_l\) 和 \(son_r\) 之一。当去除一个儿子之后，以该儿子为根的子树中的点（除了去除的儿子）全部存活，另一个儿子接下来被感染，问题转化为了被感染的儿子的那棵子树能够存活多少，成了原问题的子问题。那么，就能得到：\(f_i = \max(f_{son[l]} + size_{son[r]} - 1 , f_{son[r]} + size_{son[l]} - 1)\)，其中 \(size\) 存子树大小，要减 \(1\) 是因为我们去除的那个点不算存活。

数组要开够！

代码

#include<iostream>
#include<cstdio>
#define maxn 300005
using namespace std;
int T,n,u,v; int f[maxn],size[maxn]; struct node{int to,nex;}a[maxn*2]; int head[maxn],tot=0;
void add(int from,int to){a[++tot].to=to;a[tot].nex=head[from];head[from]=tot;}
void set(){tot=0; for(int i=1;i<=n;i++){head[i]=0;f[i]=0;size[i]=0;}}
void dfs(int p,int fa){
	size[p]=1; int res=0;
	for(int i=head[p];i;i=a[i].nex)
                if(a[i].to!=fa){dfs(a[i].to,p);size[p]+=size[a[i].to];res+=f[a[i].to];}
	//res 存两个儿子的 f 值之和,以便快速求出另一个儿子的 f 值 
	for(int i=head[p];i;i=a[i].nex) if(a[i].to!=fa) f[p]=max(f[p],(res-f[a[i].to])+(size[a[i].to]-1));
	//假设要去除 a[i].to 这个儿子 
}
int main(){
	scanf("%d",&T);
	while(T--){
		set(); scanf("%d",&n); for(int i=1;i<n;i++){scanf("%d%d",&u,&v); add(u,v); add(v,u);}
		dfs(1,0); printf("%d\n",f[1]);
	}
	return 0;
}