矩阵、矩阵运算及矩阵加速

矩阵的定义

矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合。 ——百度百科

我们将一个由 n*m 个数排成的 n 行 m 列的数表称为一个 n 行 m 列的矩阵，简称 n*m 矩阵，记为：

\[A\,= \begin{bmatrix}a_{1,1}&a_{1,2}&\cdots&a_{1,m}\\a_{2,1}&a_{2,2}&\cdots&a_{2,m}\\\vdots&\vdots&\ddots&\vdots\\a_{n,1}&a_{n,2}&\cdots&a_{n,m}\end{bmatrix} \]

基本运算

矩阵加法

两个同型矩阵（行数和列数分别相同）可以相加。一个 n*m 矩阵与另一个 n*m 矩阵相乘，得到的还是一个 n*m 矩阵，得到的矩阵的每个元素等于两个矩阵中对应的元素之和。例如：

\[\begin{bmatrix}1&5\\2&4\end{bmatrix} + \begin{bmatrix}3&5\\4&6\end{bmatrix} = \begin{bmatrix}1+3&5+5\\2+4&4+6\end{bmatrix} = \begin{bmatrix}4&10\\6&10\end{bmatrix} \]

矩阵减法

与矩阵加法同理：

\[\begin{bmatrix}1&5\\2&4\end{bmatrix} - \begin{bmatrix}3&5\\4&6\end{bmatrix} = \begin{bmatrix}1-3&5-5\\2-4&4-6\end{bmatrix} = \begin{bmatrix}-2&0\\-2&-2\end{bmatrix} \]

矩阵数乘

一个数（实数复数均可）与一个 n*m 的矩阵相乘，得到的还是一个 n*m 的矩阵，这个矩阵的每个元素等于原矩阵对应的元素乘那个数。例如：

\[3 \cdot \begin{bmatrix}1&5\\2&4\end{bmatrix} = \begin{bmatrix}3\times1&3\times5\\3\times2&3\times4\end{bmatrix} = \begin{bmatrix}3&15\\6&12\end{bmatrix} \]

性质

（以下 \(\lambda\) 和 \(\mu\) 为数，\(A\) 和 \(B\) 为矩阵）

1. \(\lambda\cdot(\mu\cdot A) = \mu\cdot(\lambda\cdot A) = (\lambda\mu)\cdot A\)
2. \((\lambda+\mu)\cdot A = \lambda\cdot A+\mu\cdot A\)
3. \(\lambda\cdot(A + B) = \lambda\cdot A + \lambda\cdot B\)

矩阵转置

顾名思义，矩阵转置就是将矩阵的行和列相互交换。一个 n*m 的矩阵转置得到一个 m*n 的矩阵。例如：

\[\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix}^T = \begin{bmatrix}1&2\\3&4\\5&6\end{bmatrix} \]

性质

1. \((A^T)^T = A\)
2. \((\lambda\cdot A)^T = \lambda\cdot A^T\)

矩阵乘法

两个矩阵可以相乘，当且仅当第一个矩阵的列数与第二个矩阵的行数相同。若一个 n*p 的矩阵 A 与一个 p*m 的矩阵 B 相乘，会得到一个 n*m 的矩阵 C。记 A、B、C 中的元素为 a、b、c，就有：\(c_{i,j} = \sum\limits_{k=1}^{p}{a_{i,p}*b_{p,j}}\) 。例如：

\[\begin{aligned} \begin{bmatrix}1&3&5\\2&4&6\end{bmatrix} \times \begin{bmatrix}-1&-2\\-3&-4\\-5&-6\end{bmatrix}&= \begin{bmatrix}1\times (-1) + 3\times(-3) + 5\times(-5)&1\times (-2) + 3\times(-4) + 5\times(-6)\\2\times (-1) + 4\times(-3) + 6\times(-5)&2\times (-2) + 4\times(-4) + 6\times(-6)\end{bmatrix} \\&= \begin{bmatrix}-35&-44\\-44&-56\end{bmatrix} \end{aligned} \]

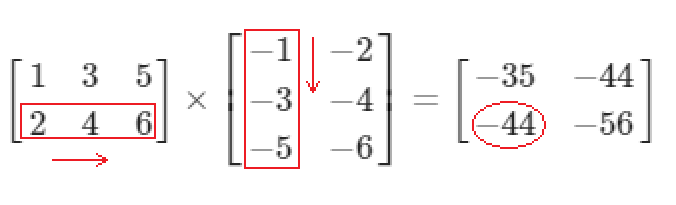
性质

1. \((A\times B)\times C = A\times(B\times C)\)
2. \((A + B)\times C = A\times C + B\times C\)
3. \(C\times (A + B) = C\times A + C\times B\)
4. \(\lambda\cdot(A\times B) = (\lambda\cdot A)\times B = A\times(\lambda\cdot B)\)
5. \((A\times B)^T = B^T\times A^T\)

特殊矩阵

单位矩阵

顾名思义，单位矩阵相当于 “1” 的存在，任何矩阵 A 乘单位矩阵 I 都等于它本身，即 \(A\times I = A\)。
由矩阵乘法，我们可以得到单位矩阵（对角线全部为 1）：

\[I = \begin{bmatrix}1&0&0&\cdots&0\\0&1&0&\cdots&0\\0&0&1&\cdots&0\\\vdots&\vdots&\vdots&\ddots&\vdots\\0&0&0&\cdots&1\end{bmatrix} \]

矩阵快速幂

给定一个 n*n 的矩阵 A，求 \(A^k\)。
类比整数的快速幂，我们将指数 k 分解为二进制，根据下式求解：

\[A^k=\begin{cases}(A^{\frac{k}{2}})^2&k\bmod 2 = 0\\ (A^{\left\lfloor\frac{k}{2}\right\rfloor})^2\times A&k\bmod 2 = 1\end{cases} \]

只需要把整数快速幂中的 “1” 变成单位矩阵、乘法变成矩阵乘法即可。

#include<iostream>
#include<cstdio>
#define maxn 105
#define ll long long
#define mod 1000000007
using namespace std;
int n; ll k,a[maxn][maxn],ans[maxn][maxn];
void mul1(){//ans*=a
	ll res[maxn][maxn];
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){
		res[i][j]=0;for(int k=1;k<=n;k++){res[i][j]+=(ans[i][k]*a[k][j])%mod;res[i][j]%=mod;}
	}
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) ans[i][j]=res[i][j]%mod;
}
void mul2(){//a*=a
	ll res[maxn][maxn];
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++){
		res[i][j]=0;for(int k=1;k<=n;k++){res[i][j]+=(a[i][k]*a[k][j])%mod;res[i][j]%=mod;}
	}
	for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) a[i][j]=res[i][j]%mod;
}
void qp(){
	for(int i=1;i<=n;i++) ans[i][i]=1;
	while(k){if(k&1) mul1(); mul2(); k>>=1;}
	for(int i=1;i<=n;i++){for(int j=1;j<=n;j++) printf("%lld ",ans[i][j]); printf("\n");}
}
int main(){
	scanf("%d%lld",&n,&k); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) scanf("%lld",&a[i][j]); qp();
	return 0;
}

矩阵加速（数列）

矩阵加速被用来快速求解数列的某一项，通过构造矩阵并运用矩阵快速幂来减小时间。
下面是构造矩阵的一些例子。（参考）

例 1

\[f_i = \begin{cases}1&i \in\{1,2\}\\f_{i-1}+f_{i-2}&i\ge 3\end{cases} \]

这就是斐波那契数列。我们若要快速地求解第 n 项，我们可以将前两项放入矩阵得到 \(F = \begin{bmatrix}1&1\end{bmatrix}\)，并构造出矩阵 A，使得其满足以下式子：

\[\begin{bmatrix}f_i&f_{i+1}\end{bmatrix} \times A = \begin{bmatrix}f_{i+1}&f_{i+2}\end{bmatrix} = \begin{bmatrix}f_{i+1}&f_i + f_{i+1}\end{bmatrix} \]

这样我们将原矩阵 \(F = \begin{bmatrix}1&1\end{bmatrix}\)（即 \(\begin{bmatrix}f_1&f_2\end{bmatrix}\)）乘 \(A^{n-1}\) 就能够得到 \(\begin{bmatrix}f_n&f_{n+1}\end{bmatrix}\) 了，此时我们就得到了 \(f_n\)。
下面我们构造矩阵 A。

首先我们发现一个 1*2 的矩阵乘 A 得到的还是一个 1*2 的矩阵，那么 A 就应该是 2*2 的矩阵。
然后看 A 的第一列，应该满足：\(f_i\times a_{1,1} + f_{i+1}\times a_{2,1} = f_{i+1}\)，解得 \(\begin{cases}a_{1,1} = 0\\a_{2,1} = 1\end{cases}\)；
同理看 A 的第二列，满足：\(f_i\times a_{1,2} + f_{i+1}\times a_{2,2} = f_i + f_{i+1}\)，解得 \(\begin{cases}a_{1,2} = 1\\a_{2,2} = 1\end{cases}\)。
故 \(A = \begin{bmatrix}0&1\\1&1\end{bmatrix}\)。

例 2

\[f_i = \begin{cases}1&i \in\{1,2\}\\f_{i-1}+f_{i-2}+1&i\ge 3\end{cases} \]

同理，我们将初始的两项和递推时要用到的常数 1 放入初始矩阵 F 得到 \(F = \begin{bmatrix}1&1&1\end{bmatrix}\)，而此时我们要构造的 A 矩阵就要满足：

\[\begin{bmatrix}f_i&f_{i+1}&1\end{bmatrix} \times A = \begin{bmatrix}f_{i+1}&f_{i+2}&1\end{bmatrix} = \begin{bmatrix}f_{i+1}&f_i + f_{i+1} + 1&1\end{bmatrix} \]

构造时，首先我们还是可以分析出 A 应该为 3*3 矩阵。
然后看 A 的第一列：\(f_i\times a_{1,1} + f_{i+1}\times a_{2,1} + 1\times a_{3,1} = f_{i+1}\)，解得 \(\begin{cases}a_{1,1} = 0\\a_{2,1} = 1\\a_{3,1} = 0\end{cases}\)；
第二列：\(f_i\times a_{1,2} + f_{i+1}\times a_{2,2} + 1\times a_{3,2} = f_i + f_{i+1} + 1\)，解得 \(\begin{cases}a_{1,2} = 1\\a_{2,2} = 1\\a_{3,2} = 1\end{cases}\)；
第三列：\(f_i\times a_{1,3} + f_{i+1}\times a_{2,3} + 1\times a_{3,3} = 1\)，解得 \(\begin{cases}a_{1,3} = 0\\a_{2,3} = 0\\a_{3,3} = 1\end{cases}\)。
故 \(A = \begin{bmatrix}0&1&0\\1&1&0\\0&1&1\end{bmatrix}\)。

例 3（洛谷的模板题）

\[f_i = \begin{cases}1&i \in\{1,2,3\}\\f_{i-1}+f_{i-3}&i\ge 4\end{cases} \]

我们将初始值放入 F 得到 \(F = \begin{bmatrix}1&1&1\end{bmatrix}\)，此时构造的 A 满足：

\[\begin{bmatrix}f_i&f_{i+1}&f_{i+2}\end{bmatrix} \times A = \begin{bmatrix}f_{i+1}&f_{i+2}&f_{i+3}\end{bmatrix} = \begin{bmatrix}f_{i+1}&f_{i+2}&f_i + f_{i+2}\end{bmatrix} \]

分析得到 A 为 3*3 的矩阵。
A 的第一列：\(f_i\times a_{1,1} + f_{i+1}\times a_{2,1} + f_{i+2}\times a_{3,1} = f_{i+1}\)，解得 \(\begin{cases}a_{1,1} = 0\\a_{2,1} = 1\\a_{3,1} = 0\end{cases}\)；
第二列：\(f_i\times a_{1,2} + f_{i+1}\times a_{2,2} + f_{i+2}\times a_{3,2} = f_{i+2}\)，解得 \(\begin{cases}a_{1,2} = 0\\a_{2,2} = 0\\a_{3,2} = 1\end{cases}\)；
第三列：\(f_i\times a_{1,3} + f_{i+1}\times a_{2,3} + f_{i+2}\times a_{3,3} = f_i + f_{i+2}\)，解得 \(\begin{cases}a_{1,3} = 1\\a_{2,3} = 0\\a_{3,3} = 1\end{cases}\)。
所以 \(A = \begin{bmatrix}0&0&1\\1&0&0\\0&1&1\end{bmatrix}\)。

代码

#include<iostream>
#include<cstdio>
#define maxn 3000005
#define ll long long
#define mod 1000000007
using namespace std;
ll T,n; ll ans[2][4]={{0,0,0,0},{0,1,1,1}},a[4][4]={{0,0,0,0},{0,0,0,1},{0,1,0,0},{0,0,1,1}};
void mul1(){//ans*=a
	ll res[2][4];
	for(int i=1;i<=3;i++){res[1][i]=0; for(int k=1;k<=3;k++) res[1][i]=(res[1][i]+(ans[1][k]*a[k][i]%mod))%mod;}
	for(int i=1;i<=3;i++) ans[1][i]=res[1][i]%mod;
}
void mul2(){//a*=a
	ll res[4][4];
	for(int i=1;i<=3;i++) for(int j=1;j<=3;j++){
		res[i][j]=0; for(int k=1;k<=3;k++) res[i][j]=(res[i][j]+(a[i][k]*a[k][j]%mod))%mod;
	}
	for(int i=1;i<=3;i++) for(int j=1;j<=3;j++) a[i][j]=res[i][j]%mod;
}
void doit(){
	for(int i=0;i<=1;i++) for(int j=0;j<=3;j++) ans[i][j]=0; ans[1][1]=ans[1][2]=ans[1][3]=1;
	for(int i=0;i<=3;i++) for(int j=0;j<=3;j++) a[i][j]=0; a[1][3]=a[2][1]=a[3][2]=a[3][3]=1;
	while(n){ if(n&1) mul1(); mul2(); n>>=1; }
	printf("%lld\n",ans[1][1]);
}
int main(){
	scanf("%lld",&T); while(T--){scanf("%lld",&n);n--;doit();}
	return 0;
}

例 4

\[f_i = \begin{cases}1&i \in\{1,2\}\\f_{i-1}+f_{i-2}+i+1&i\ge 3\end{cases} \]

我们将初值与递推要用的 n 和 1 放入矩阵 F 得到 \(F = \begin{bmatrix}1&1&3&1\end{bmatrix}\)（由 A 满足的条件知第三项为 i+2，初始矩阵中 i = 1，故第三项为 3。合理的构造顺序应先为矩阵间的关系再到初始矩阵），此时 A 满足：

\[\begin{bmatrix}f_i&f_{i+1}&i+2&1\end{bmatrix} \times A = \begin{bmatrix}f_{i+1}&f_{i+2}&i+3&1\end{bmatrix} = \begin{bmatrix}f_{i+1}&f_i + f_{i+1} + (i+2) + 1&i+3&1\end{bmatrix} \]

同理计算后可以得到 \(A = \begin{bmatrix}0&1&0&0\\1&1&0&0\\0&1&1&0\\0&1&1&1\end{bmatrix}\)。

例 5

\[\begin{aligned} f_i &= \begin{cases}1&i \in\{1,2\}\\f_{i-1}+f_{i-2}&i\ge 3\end{cases} \\s_i &= \sum\limits_{x=1}^{i}{f_x} \end{aligned} \]

此时 f 仍为斐波那契数列，s 为其前缀和。同理我们可以构造初始矩阵 \(F = \begin{bmatrix}1&1&1\end{bmatrix}\)，和 A 满足的条件：

\[\begin{bmatrix}f_i&f_{i+1}&s_i\end{bmatrix} \times A = \begin{bmatrix}f_{i+1}&f_{i+2}&s_{i+1}\end{bmatrix} = \begin{bmatrix}f_{i+1}&f_i + f_{i+1}&s_i + f_{i+1}\end{bmatrix} \]

计算得到 \(A = \begin{bmatrix}0&1&0\\1&1&1\\0&0&1\end{bmatrix}\)。