线段树

线段树

引入

例：P3372【模板】线段树 1

题意是，给定一个长度为\(n\)的序列\(a\)，有\(q\)次操作，每次操作有以下两种：

1. 给出\(l,r,q\)，表示将区间\([l,r]\)内的每个数\(+k\)；
2. 给出\(l,r\)，表示求\(\sum\limits_{i=l}^{r}{a_i}\)。

范围：\(1\le n,q\le 10^5\)

分析一下，如果暴力求解，那么复杂度是\(O(qn)\)，显然过不去。所以，我们就要维护线段树解决这道题目。

简介

线段树是算法竞赛中常用的用来维护区间信息的数据结构。
线段树可以在\(O(logN)\)的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。 ----选自\(OI-WIKI\)

所以，使用线段树能使此题的复杂度改进为\(O(q\,logn)\)
什么是线段树呢？简而言之，刚才的暴力最大的缺点就是每次求值都要循环求，这样太慢了，于是我们想到利用二分求值，并将其融合进二叉树中，于是就有了线段树。

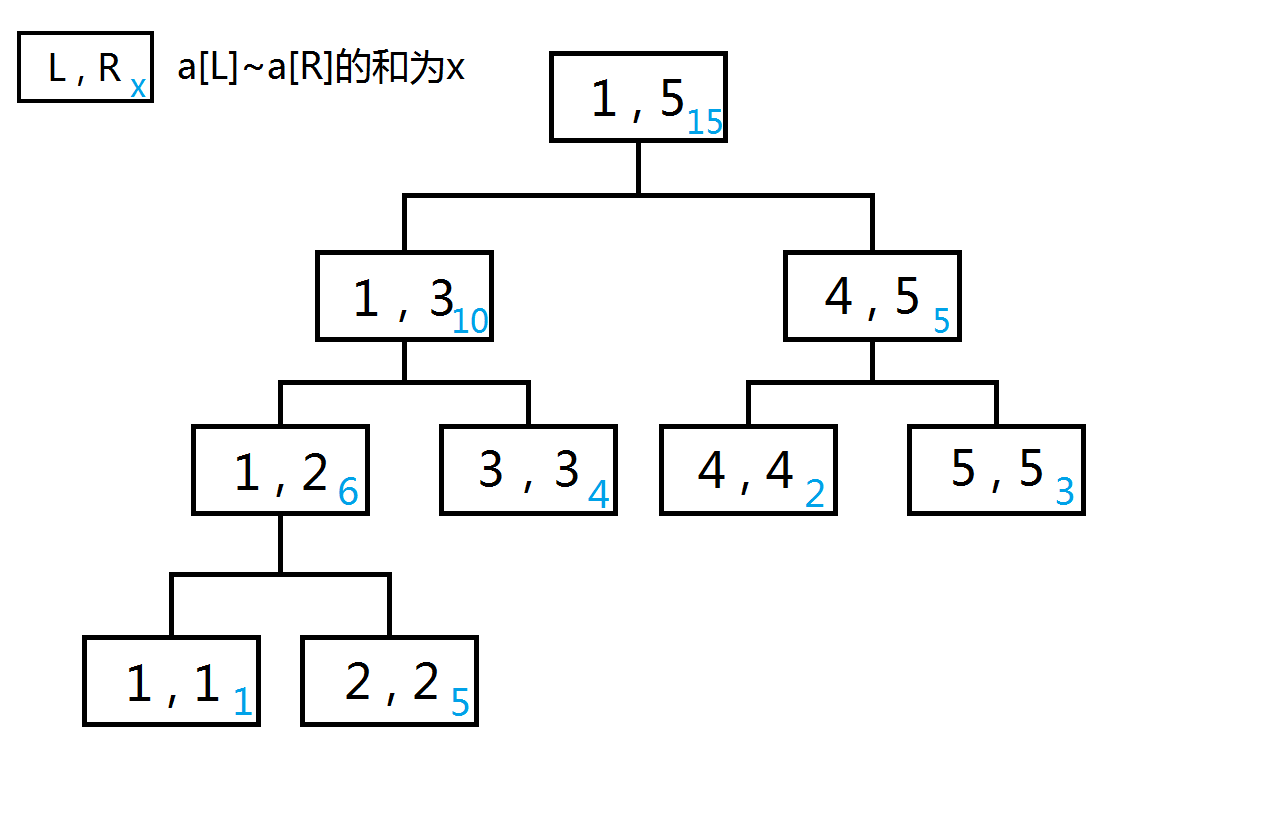
如图，每一个框表示树的一个节点，其有\(3\)个值\(l,r,sum\)，其中\(l,r\)表示它所代表的区间，\(sum\)（图中蓝字）表示这段区间的和，即\(a_i.sum=\sum\limits_{x=a[i].l}^{a[i].r}{in_x}\)（用\(a\)表示存线段树的结构体，\(in\)数组存序列元素，下同）
我们发现，若一个节点\(i\)存的区间为\([l,r](l<r)\)，那么根据二分的思想，它的左儿子\(i*2\)存的区间即为\([l,\dfrac{l+r}{2}]\)，右儿子\(i*2+1\)存的区间即为\([\dfrac{l+r}{2}+1,r]\)，则\(a[i].sum=a[i*2].sum+a[i*2+1].sum\)
于是，我们掌握了基本的线段树的思想，那么，具体过程如何呢？

基础思路——单点修改、区间查询

递归建树

首先我们要建立一棵线段树
每个线段树的节点有三个值：\(l,r,sum\)，这些都是我们建树函数的参数。又因为每个节点\(i\)的左右儿子编号分别是\(i*2,i*2+1\)（二叉树性质），那么我们就可以写出建树函数

• 代码

void build(ll i,ll l,ll r){
	a[i].l=l;//区间左端点
	a[i].r=r;//区间右端点
	if(l==r){//若为叶子节点
		a[i].sum=in[l];//区间和即为对应的序列原值
		return;
	}
	build(i*2,l,(l+r)/2);//左儿子
	build(i*2+1,(l+r)/2+1,r);//右儿子
	a[i].sum=a[i*2].sum+a[i*2+1].sum;//该区间的值等于两孩子的值之和
	return;
}

单点修改

如图，假设我们修改\(in_2\)的值，那么我们在线段树中就应该先遍历找到\([2,2]\)的节点，修改其\(sum\)值，再一路更新上去
遍历可以得到结果
那么，如何找要修改的点呢？

很简单，因为是修改单个点，所以若区间\([l,r]\)中有要修改的点\(p\),那么它不是在区间\([l,mid]\)里就是在区间\([mid+1,r]\)里（\(mid=\dfrac{l+r}{2}=a[i*2].r\)），故我们只需要判断\(p\)点在哪个区间里即可。
若\(p\le mid\)，则其在区间\([l,mid]\)中，搜\(i\)的左儿子（如图中\(p_1\)）；否则在区间\([mid+1,r]\)中，搜右儿子（如图中\(p_2\)）

• 代码

void add(int i,int point,int pluss){//in[point]要加上pluss
	if(a[i].l==a[i].r){//搜到叶子了,此时a[i].l==a[i].r==point
		a[i].sum+=pluss;
		return;
	}
	if(a[i*2].r>=point){
		add(i*2,point,pluss);
	}else{
		add(i*2+1,point,pluss);
	}
	a[i].sum=a[i*2].sum+a[i*2+1].sum;//记得更新点的sum值
	return;
}

区间查询

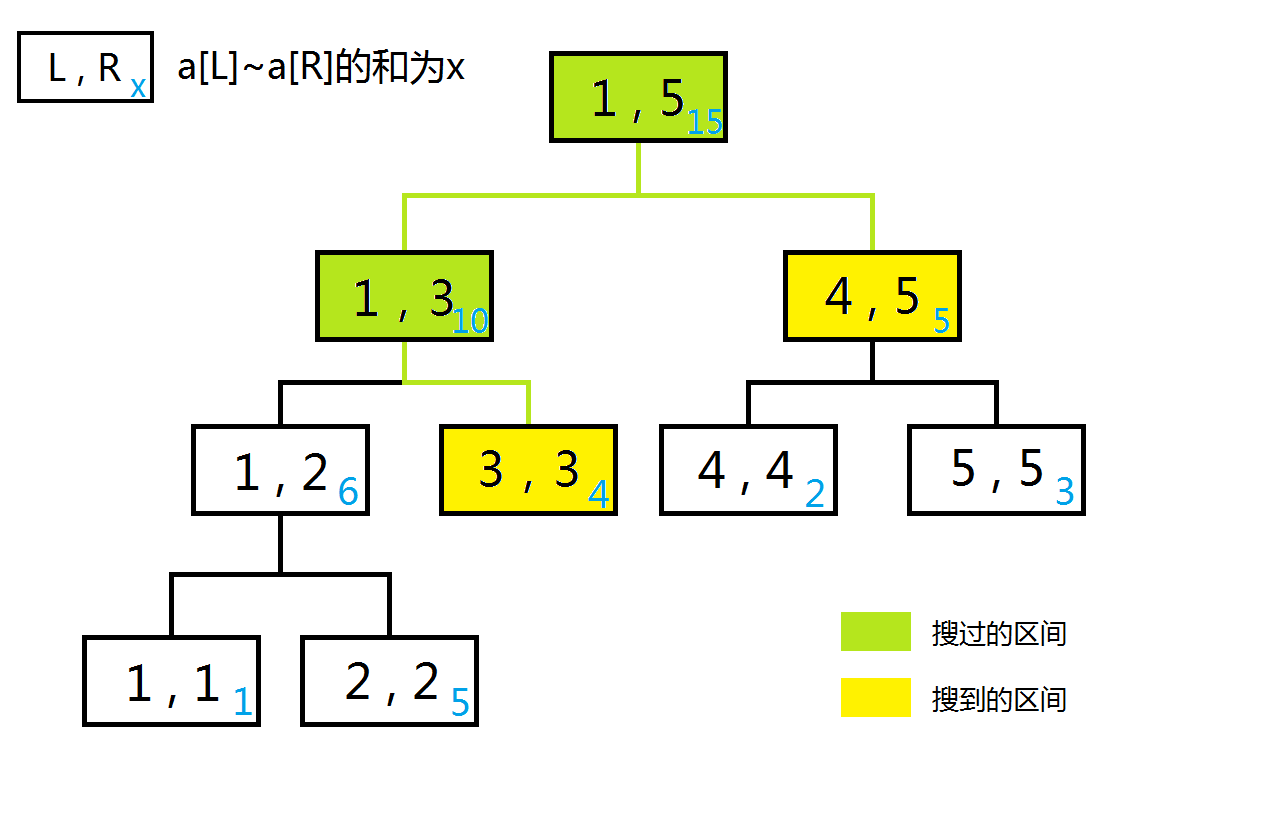
如图，若我们想要搜索\([3,5]\)的和，我们其实不用搜到\([3,3],[4,4],[5,5]\)四个区间的和再相加，只需搜\([3,3],[4,5]\)两个区间的和相加就行了（因为\([4,5]\)包含的就是\(in_4\sim in_5\)的和），所以我们发现，对于搜索函数\(search\)来说，搜到一个区间\([l,r]\)时，假设要找的区间为\([sl,sr]\)：

1. 若\(sl\le l\&\&sr\ge r\)，说明这个区间完全在要搜的区间里，直接返回\(a[i].sum\)即可（如下图\([sl_1,sr_1]\)）
2. 若\(mid\ge sl\)，说明这个区间的左儿子与要搜的区间有交集，搜左儿子（如下图\([sl_2,sr_2],[sl_4,sr_4]\)）
3. 若\(mid+1\le sr\)，说明这个区间的右儿子与要搜的区间有交集，搜右儿子（如下图\([sl_3,sr_3],[sl_4,sr_4]\)）

由上面的图也可知道，一个区间可以同时满足第\(2,3\)个条件（如上图\([sl_4,sr_4]\)），故应写两个\(if\)而非\(if + else\)

• 代码

ll search(ll i,ll l,ll r){//要搜[l,r]区间
	if(a[i].l>=l&&a[i].r<=r){完全包含
		return a[i].sum;
	}
	ll ans=0;
	if(l<=a[i*2].r){//左儿子包含
		ans+=search(i*2,l,r);
	}
        //这里不能写else (if)而要再写一个if
	if(r>=a[i*2+1].l){//右儿子包含
		ans+=search(i*2+1,l,r);
	}
	return ans;
}

例：P3374 【模板】树状数组 1

单点修改、区间查询的模板题，综合一下上述代码即可。

• 代码

#include<iostream>
#include<cstdio>
#define maxn 500005
#define ll long long
using namespace std;
ll n,q,opt,l,r,k;
ll in[maxn];
struct node{
	ll l,r,sum;
	ll lt;
}a[maxn*4];
void build(ll i,ll l,ll r){
	a[i].l=l;
	a[i].r=r;
	if(l==r){
		a[i].sum=in[l];
		return;
	}
	build(i*2,l,(l+r)/2);
	build(i*2+1,(l+r)/2+1,r);
	a[i].sum=a[i*2].sum+a[i*2+1].sum;
	return;
}
void add(int i,int point,int pluss){
	if(a[i].l==a[i].r){
		a[i].sum+=pluss;
		return;
	}
	if(a[i*2].r>=point){
		add(i*2,point,pluss);
	}else{
		add(i*2+1,point,pluss);
	}
	a[i].sum=a[i*2].sum+a[i*2+1].sum;
	return;
}
ll search(ll i,ll l,ll r){
	if(a[i].l>=l&&a[i].r<=r){
		return a[i].sum;
	}
	ll ans=0;
	if(l<=a[i*2].r){
		ans+=search(i*2,l,r);
	}
	if(r>=a[i*2+1].l){
		ans+=search(i*2+1,l,r);
	}
	return ans;
}
int main(){
	scanf("%lld%lld",&n,&q);
	for(int i=1;i<=n;i++){
		scanf("%lld",&in[i]);
	}
	build(1,1,n);
	while(q--){
		scanf("%lld",&opt);
		if(opt==1){
			scanf("%lld%lld",&l,&k);
			add(1,l,k);
		}else if(opt==2){
			scanf("%lld%lld",&l,&r);
			printf("%lld\n",search(1,l,r));
		}
	}
	return 0;
}

懒标优化——区间修改(加法)、区间查询

区间修改

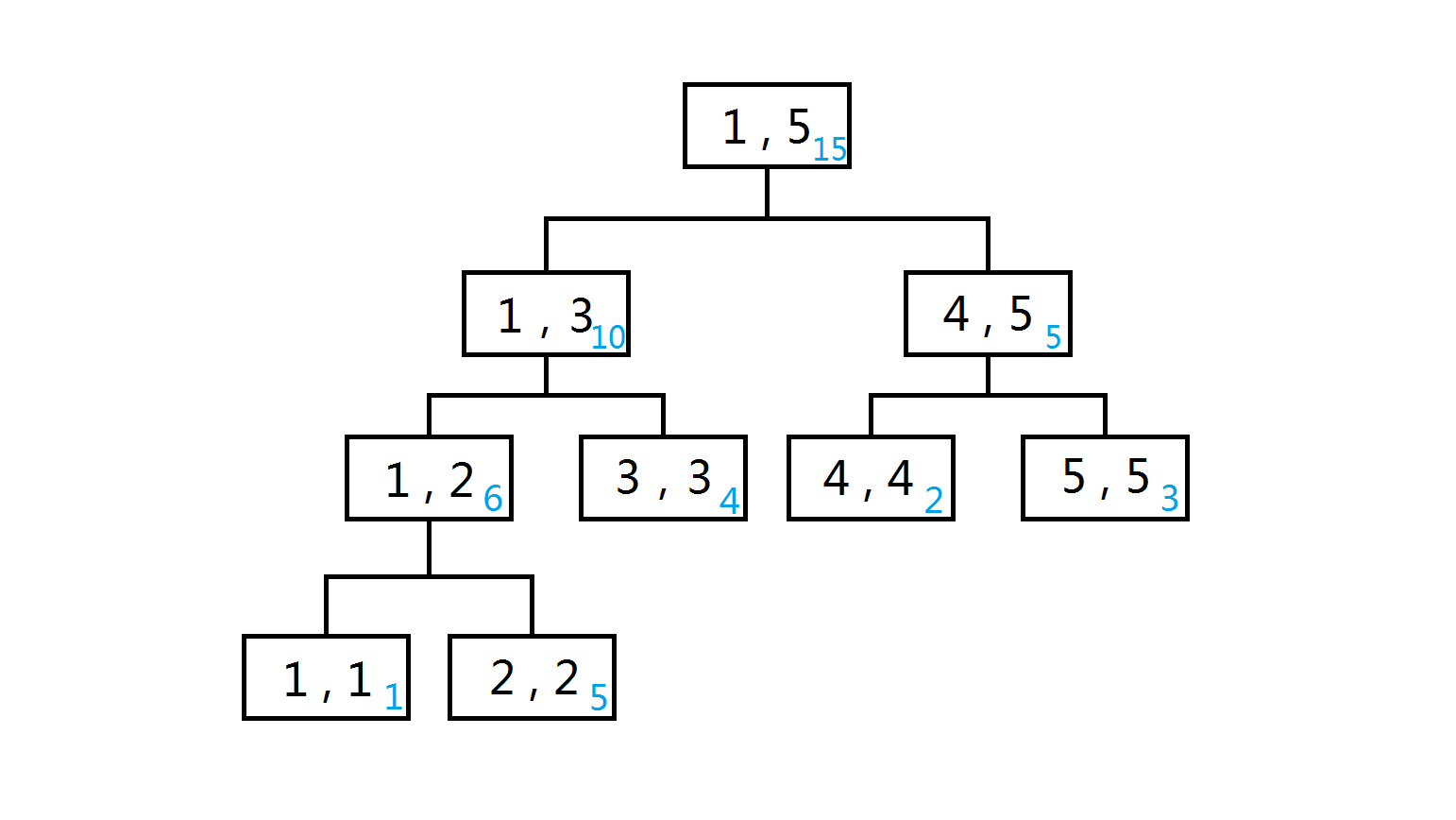
还是这张图，若我们想更改\([2,4]\)区间，若一个个单点修改复杂度甚至会大于暴力，所以，我们想是否可以和区间查询一样，若**区间完全包含于要更改的区间内就可以不继续搜呢？

懒标记优化

\(lazytag\)（即懒标记）优化的主要思想是：若搜到的这个区间完全包含于要加值的区间内，则不继续往下搜，将这个点的\(lt+=pluss\)，\(sum+=(a[i].r-a[i].l+1)*pluss\)（\(lt\)为懒标记，\(pluss\)是要加的数）
理解起来也不难，\(a[i].r-a[i].l+1\)是这个区间内的元素个数，因为这个区间完全包含于要加值的区间，所以它的所有元素都会被加上\(pluss\)，所以这个节点的\(sum\)总体增加了\((a[i].r-a[i].l+1)*pluss\)

void add(ll i,ll l,ll r,ll pluss){
	if(a[i].l>=l&&a[i].r<=r){
		a[i].lt+=pluss;
		a[i].sum+=pluss*(a[i].r-a[i].l+1);
		return;
	}
	pushdown(i);//下文讲
	if(l<=a[i*2].r){
		add(i*2,l,r,pluss);
	}
	if(r>=a[i*2+1].l){
		add(i*2+1,l,r,pluss);
	}
	a[i].sum=a[i*2].sum+a[i*2+1].sum;
	return;
}

但是若要求它的孩子的值怎么办呢？因为我们存了这个点加过的懒标的值，所以，我们可以创建一个函数（叫做\(pushdown\)），将这个节点欠的\(lt\)的值还给左右儿子：

void pushdown(ll i){
	if(a[i].lt){//懒标记不为0即有懒标记要给左右儿子
		a[i*2].lt+=a[i].lt;//左儿子懒标记加上
		a[i*2].sum+=a[i].lt*(a[i*2].r-a[i*2].l+1);//左儿子的sum加上对应的值
		a[i*2+1].lt+=a[i].lt;//右儿子同理
		a[i*2+1].sum+=a[i].lt*(a[i*2+1].r-a[i*2+1].l+1);
		a[i].lt=0;//清空
	}
	return;
}

所以，整合起来我们就得到了最终代码：

例：P3372【模板】线段树 1

#include<iostream>
#include<cstdio>
#define maxn 100005
#define ll long long
using namespace std;
ll n,q,opt,l,r,k;
ll in[maxn];
struct node{
	ll l,r,sum;
	ll lt;
}a[maxn*4];
void build(ll i,ll l,ll r){
	a[i].l=l;
	a[i].r=r;
	a[i].lt=0;
	if(l==r){
		a[i].sum=in[l];
		return;
	}
	build(i*2,l,(l+r)/2);
	build(i*2+1,(l+r)/2+1,r);
	a[i].sum=a[i*2].sum+a[i*2+1].sum;
	return;
}
void pushdown(ll i){
	if(a[i].lt){
		a[i*2].lt+=a[i].lt;
		a[i*2].sum+=a[i].lt*(a[i*2].r-a[i*2].l+1);
		a[i*2+1].lt+=a[i].lt;
		a[i*2+1].sum+=a[i].lt*(a[i*2+1].r-a[i*2+1].l+1);
		a[i].lt=0;
	}
	return;
}
void add(ll i,ll l,ll r,ll pluss){
	if(a[i].l>=l&&a[i].r<=r){
		a[i].lt+=pluss;
		a[i].sum+=pluss*(a[i].r-a[i].l+1);
		return;
	}
	pushdown(i);
	if(l<=a[i*2].r){
		add(i*2,l,r,pluss);
	}
	if(r>=a[i*2+1].l){
		add(i*2+1,l,r,pluss);
	}
	a[i].sum=a[i*2].sum+a[i*2+1].sum;
	return;
}
ll search(ll i,ll l,ll r){
	if(a[i].l>=l&&a[i].r<=r){
		return a[i].sum;
	}
	pushdown(i);
	ll ans=0;
	if(l<=a[i*2].r){
		ans+=search(i*2,l,r);
	}
	if(r>=a[i*2+1].l){
		ans+=search(i*2+1,l,r);
	}
	return ans;
}
int main(){
	scanf("%lld%lld",&n,&q);
	for(int i=1;i<=n;i++){
		scanf("%lld",&in[i]);
	}
	build(1,1,n);
	while(q--){
		scanf("%lld",&opt);
		if(opt==1){
			scanf("%lld%lld%lld",&l,&r,&k);
			add(1,l,r,k);
		}else if(opt==2){
			scanf("%lld%lld",&l,&r);
			printf("%lld\n",search(1,l,r));
		}
	}
	return 0;
}

未完待续…