网络流24题 - 5
题目顺序按照洛谷“\(\color{#13C2C2}{网络流24题}\)”标签按难度排序。
题目的字体颜色为洛谷此题难度的颜色。
本人的题单: 网络流24题
P4013 \(\color{#9D3DCF}{数字梯形问题}\)
题目大意
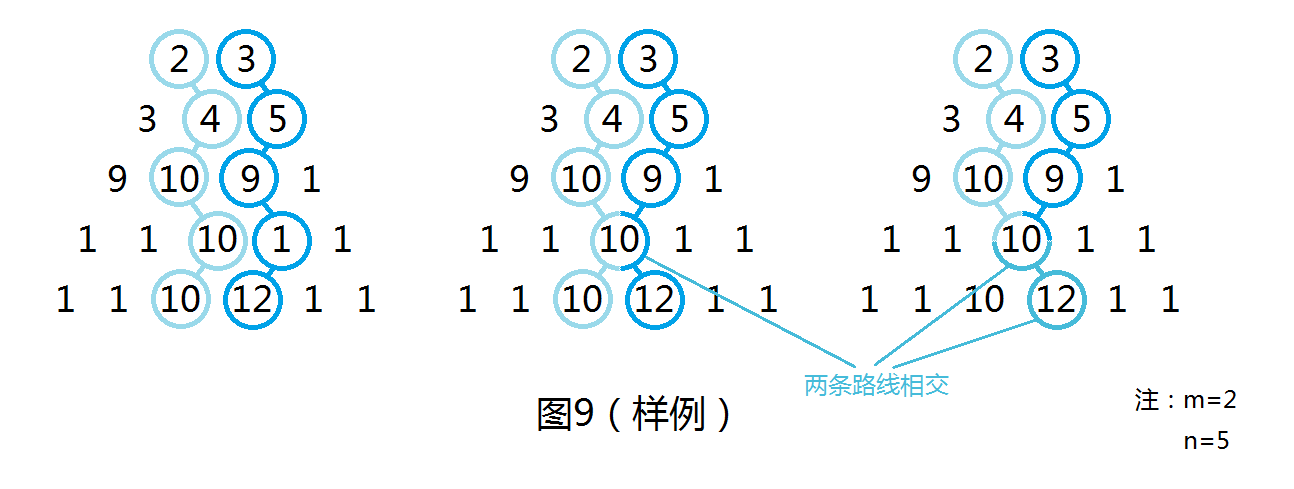
给定一个上底为\(m\),高为\(n\)的、由数字构成的梯形(如下图)。分别构造从顶部\(m\)个点分别出发的\(m\)条符合以下要求的路径(每个点只能走到其左下或右下的点),输出路径经过的数字和的最大值(样例答案分别为\(66,75,77\)):
- \(m\)条路径都互不相交;
- \(m\)条路径只可以在数字处相交;
- \(m\)条路径既可以在数字处相交也可以在边上相交。
思路
看着有很多问,实际上都可以复制,改一点就好了
- 第\((1)\)问
建立超级源点\(s\)与超级汇点\(t\),\(s\)与第一行\(m\)个点相连,\(f=1,c=0\)以免费提供初始流量;最后一行\(m+n-1\)个点与\(t\)相连,\(f=1,c=0\)作为路径结束点。因为每个点最多只能被一条路径选择(最多只能经过\(1\)次),故拆成入点和出点,中间连\(f=1,c=-in_i\)的边作为代价(\(in_i\)为点上的数字,为负是因为本题要求最大值)。同时每个点和左下、右下的点连\(f=1,c=0\)的边,表示最多通过一条路径。此时跑最小费用最大流即可。 - 第\((2)\)问
因为点可以被选很多次,故将入点出点间的\(f\)改为\(\infty\)即可。 - 第\((3)\)问
因为边也可以被选很多次,故在第\((2)\)问的基础上再把点与左下右下点连的边的\(f\)改为\(\infty\)即可。
细节
- 第\((2)\)问中最底部的点与\(t\)的权值应该为\(\infty\),因为路线可以汇集在此(\(\color{rgb(231,76,60)}{WA}\ \ On\ \ Test4\))
- 存放数字的数组\(in\)规模应为\(in[25][55]\),不能开成\(in[25][25]\),会炸掉(\(\color{rgb(231,76,60)}{WA}\ \ On\ \ Tests1\ \&\ 2\))
代码
比较长,没有压行
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 2005
#define maxm 50005
#define ll long long
#define inf 0x3fffffff
using namespace std;
int m,n,s,t;
int in[25][25];
int head[maxn],cnt=1;
struct node{
int to,dis,cost,nex;
}a[maxm*2];
void add(int from,int to,int dis,int cost){
a[++cnt].to=to;a[cnt].dis=dis;a[cnt].cost=cost;a[cnt].nex=head[from];head[from]=cnt;
a[++cnt].to=from;a[cnt].dis=0;a[cnt].cost=-cost;a[cnt].nex=head[to];head[to]=cnt;
}
bool vis[maxn];
int costs[maxn];
bool spfa(){
memset(vis,0,sizeof(vis));
memset(costs,0x3f,sizeof(costs));
queue<int> q;
vis[s]=1;
q.push(s);
costs[s]=0;
while(!q.empty()){
int top=q.front();
q.pop();
vis[top]=0;
for(int i=head[top];i;i=a[i].nex){
if(costs[top]+a[i].cost<costs[a[i].to]&&a[i].dis){
costs[a[i].to]=costs[top]+a[i].cost;
if(!vis[a[i].to]){
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
if(costs[t]==costs[0]){
return 0;
}
return 1;
}
ll ans=0,anscost=0;
int dfs(int x,int minn){
if(x==t){
vis[t]=1;
ans+=minn;
return minn;
}
int use=0;
vis[x]=1;
for(int i=head[x];i;i=a[i].nex){
if((!vis[a[i].to]||a[i].to==t)&&costs[a[i].to]==costs[x]+a[i].cost&&a[i].dis){
int search=dfs(a[i].to,min(minn-use,a[i].dis));
if(search>0){
use+=search;
anscost+=(a[i].cost*search);
a[i].dis-=search;
a[i^1].dis+=search;
if(use==minn){
break;
}
}
}
}
return use;
}
void dinic(){
while(spfa()){
do{
memset(vis,0,sizeof(vis));
dfs(s,inf);
}while(vis[t]);
}
printf("%lld",-1*anscost);
}
void set(){
cnt=1;
memset(a,0,sizeof(0));
memset(head,0,sizeof(head));
ans=anscost=0;
}
int main(){
scanf("%d%d",&m,&n);
//第(1)问
int cntin=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m+i-1;j++){
scanf("%d",&in[i][j]);
cntin++;
add(cntin*2-1,cntin*2,1,-1*in[i][j]);
}
}
s=cntin*2+1;
t=s+1;
cntin=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m+i-1;j++){
cntin++;
if(i==1){
add(s,cntin*2-1,1,0);
}else if(i==n){
add(cntin*2,t,1,0);
}
if(i!=n){
add(cntin*2,(cntin+m+i-1)*2-1,1,0);
add(cntin*2,(cntin+m+i)*2-1,1,0);
}
}
}
dinic();printf("\n");
//第(2)问
set();
cntin=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m+i-1;j++){
cntin++;
add(cntin*2-1,cntin*2,inf,-1*in[i][j]);
}
}
s=cntin*2+1;
t=s+1;
cntin=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m+i-1;j++){
cntin++;
if(i==1){
add(s,cntin*2-1,1,0);
}else if(i==n){
add(cntin*2,t,inf,0);
}
if(i!=n){
add(cntin*2,(cntin+m+i-1)*2-1,1,0);
add(cntin*2,(cntin+m+i)*2-1,1,0);
}
}
}
dinic();printf("\n");
//第(3)问
set();
cntin=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m+i-1;j++){
cntin++;
add(cntin*2-1,cntin*2,inf,-1*in[i][j]);
}
}
s=cntin*2+1;
t=s+1;
cntin=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m+i-1;j++){
cntin++;
if(i==1){
add(s,cntin*2-1,1,0);
}else if(i==n){
add(cntin*2,t,inf,0);
}
if(i!=n){
add(cntin*2,(cntin+m+i-1)*2-1,inf,0);
add(cntin*2,(cntin+m+i)*2-1,inf,0);
}
}
}
dinic();
return 0;
}
P3355 \(\color{#9D3DCF}{骑士共存问题}\)
题目大意
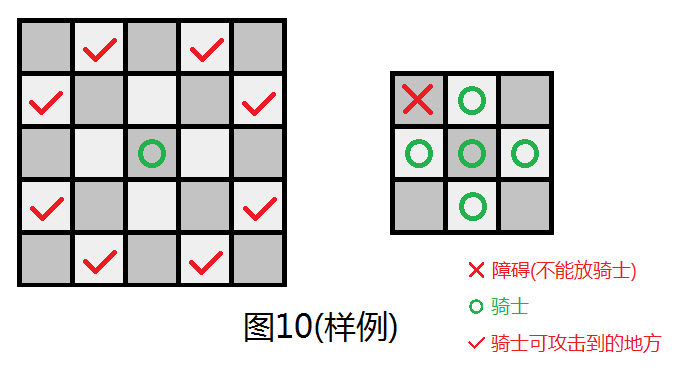
在一 \(n\times n\)的国际象棋棋盘上,有\(m\)个位置有障碍,问其余部分最能能放多少骑士,使得他们相互之间不攻击。(骑士走“日”字格,如下图左边;样例答案为\(5\),如下图右边)。
思路
我们将棋盘黑白染色,如上图左图,发现当骑士在黑色格子中时,能攻击到的全部都是白色格子,同理若其在白色格子则能攻击到的都是黑色格子。
所以,我们建立超级源点\(s\)和超级汇点\(t\),将\(s\)与所有黑色格子(横纵坐标相加为偶数)连,剩余格子与\(t\)连,\(f\)均为\(1\);每个格子与其能攻击到的格子连,\(f=\inf\)。此时跑最小割,\(\color{red}{把割掉的格子表示为不放骑士}\),这样就保证了没有可以互相攻击的骑士且割去的格子最少,答案为 格子总数\(-\)障碍数\(-\)割掉的格子数 ,即\(n^2-m-mincut\)。
细节
- 因为边很多,故数组开大一点(\(\color{rgb(157,61,207)}{RE}\ \ On\ \ Test3\))
- 根据格子横纵坐标和的奇偶染色而不是根据编号染色(\(\color{rgb(231,76,60)}{WA}\ \ On\ \ Test3\))
代码
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 40005
#define maxm 500005
#define ll long long
#define inf 0x3fffffff
using namespace std;
int n,m,s,t,x,y;
int invis[205][205];
int head[maxn],tt=1;
struct node{
int to,dis,nex;
}a[maxm*2];
void add(int from,int to,int dis){
a[++tt].to=to;a[tt].dis=dis;a[tt].nex=head[from];head[from]=tt;
a[++tt].to=from;a[tt].dis=0;a[tt].nex=head[to];head[to]=tt;
}
bool vis[maxn];
int dep[maxn],cur[maxn];
bool bfs(){
for(int i=0;i<=t;i++){
vis[i]=0;
dep[i]=inf;
cur[i]=head[i];
}
queue<int> q;
vis[s]=1;
q.push(s);
dep[s]=0;
while(!q.empty()){
int top=q.front();
q.pop();
for(int i=head[top];i;i=a[i].nex){
if(dep[top]+1<dep[a[i].to]&&a[i].dis){
dep[a[i].to]=dep[top]+1;
if(!vis[a[i].to]){
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
return dep[t]!=dep[0];
}
ll ans=0;
int dfs(int x,int minn){
if(x==t){
ans+=minn;
return minn;
}
int use=0;
for(int i=cur[x];i;i=a[i].nex){
cur[x]=i;
if(dep[a[i].to]==dep[x]+1&&a[i].dis){
int search=dfs(a[i].to,min(minn-use,a[i].dis));
if(search>0){
use+=search;
a[i].dis-=search;
a[i^1].dis+=search;
if(use==minn){
break;
}
}
}
}
return use;
}
int id(int x1,int y1){
return (x1-1)*n+y1;
}
void dinic(){
while(bfs()){
dfs(s,inf);
}
printf("%lld",n*n-m-ans);
}
int main(){
scanf("%d%d",&n,&m);
s=n*n+1;
t=s+1;
for(int i=1;i<=m;i++){
scanf("%d%d",&x,&y);
invis[x][y]=1;
}
int dx[8]={1,1,-1,-1,2,2,-2,-2},dy[8]={2,-2,2,-2,1,-1,1,-1};
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(invis[i][j]){
continue;
}
if((i+j)%2){
add(s,id(i,j),1);
for(int k=0;k<8;k++){
int nx=i+dx[k],ny=j+dy[k];
if(nx>=1&&nx<=n&&ny>=1&&ny<=n&&!invis[nx][ny]){
add(id(i,j),id(nx,ny),1e9);
}
}
}else{
add(id(i,j),t,1);
}
}
}
dinic();
return 0;
}
P3357 \(\color{#9D3DCF}{最长k可重线段集问题}\)
- 已同步至洛谷该题题解
题目大意
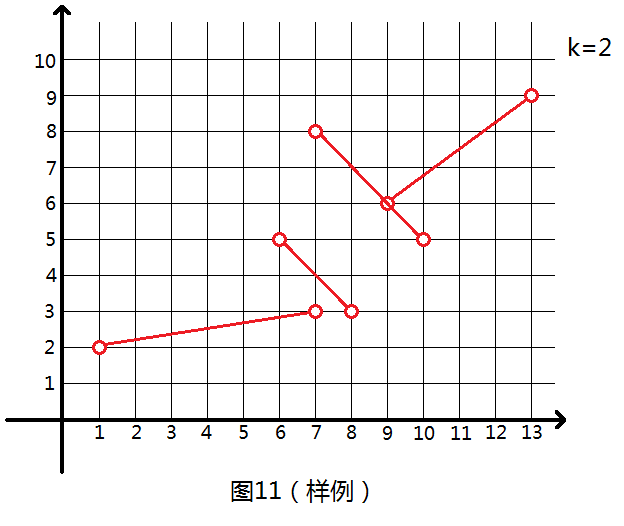
给定平面\(x-O-y\)内\(n\)个开线段(类比开区间,应该是不取两端点的线段)和正整数\(k\),要求从这些线段中选择若干个,使得任意平行\(y\)轴的直线\(x=p\)都不和大于k个线段相交,求选出线段的长度和的最大值(此处端点为\((x_1,y_1)\)和\((x_2,y_2)\)的线段长度为\(\left\lfloor{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}}\right\rfloor\))(如图\(11\),答案为\(17\),\(4\)个线段都选即可)。
思路
想到之前的P3358,我们可以发现,这一题与那题的区别就是那题在数轴上而这题在平面内,于是我们考虑:能不能将这些线段变成数轴上的区间呢?(这样就可以直接用\(P3358\)的代码了)发现可以将这些线段投影到\(x\)轴上,这样就完成了我们将线段转换到区间的愿望(如下图\(11.2\))。此时将代码改一下上交,就会获得\(9\)分的好成绩。

为什么呢?画图分析,我们发现若线段像图\(11.3\)一样不平行\(y\)轴(即\(x_1\not= x_2\))时我们的代码正确,但是一旦出现如图\(11.4\)一样的、平行于\(y\)轴的线段(即\(x_1 = x_2\)),则将其投影到\(x\)轴上后,先不说交不交的问题,甚至这条“线段”都不存在(因为是开区间所以不取两端点的值)。于是我们想到可以拆点(扩域),把区间\((x_i,x_j)\)变成\((2\times x_i,2\times x_j)\)(后文省略乘号),这样就可以空出许多奇数的点,如\(1,3,5\)等.此时若遇到平行\(y\)轴的线段就可以把区间变成\((2x_i,2x_i+1)\)。但此时又出现了一个新的问题,由于是开线段变成的开区间,那么原来区间\((x_i,x_i)\)和\((x_i,x_j)\)(假定\(x_j>x_i\))不交,但是被我们改过后区间变成了\((2x_i,2x_i+1)\)和\((2x_i,2x_j)\),之间是相交的,会导致答案错误,所以,我们应该把不平行\(y\)轴的线段变成的区间\((x_i,x_j)\)也改变,变成\((2x_i+1,2x_j)\),这样就不会出现上述的区间不交变成相交的问题了。但是这样会不会让原来相交的区间变成不交呢?可以证明不会:(如图\(11.3\))设两区间分别为\((x_1,x_2)\)和\((x_3,x_4)\),那么改变之后变成了\((2x_1+1,2x_2)\)和\((2x_3+1,2x_4)\):若原来两区间相交,则\(x_3>x_2\),更具体地,\(x_3-x_2\ge 1\)(应该是\(>0\)的,在本题中由于输入的都是整数,故\(\ge1\)),所以改变之后的\(2x_3+1-2x_2\ge 3> 1\),仍然相交;若原来两区间不交,则同理\(x_2-x_3\ge 1\),改变后的\(2x_2-(2x_3+1)\ge 1\),仍然不交。
细节
- 距离要向下取整,可以用\(cmath\)库的\(floor\)函数。
不开\(long\ long\)见祖宗(\(\color{rgb(231,76,60)}{WA}\ \ On\ \ Test4\))
代码
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<cmath>
#include<algorithm>
#define maxn 5005
#define maxm 50005
#define ll long long
#define inf 0x3fffffff
using namespace std;
ll n,k,s,t;
ll xx1[maxn],yy1[maxn],xx2[maxn],yy2[maxn],diss[maxn];
ll num[maxn],cnt=0;
ll head[maxn],tt=1;
struct node{
ll to,dis,cost,nex;
}a[maxm*2];
void add(ll from,ll to,ll dis,ll cost){
a[++tt].to=to;a[tt].dis=dis;a[tt].cost=cost;a[tt].nex=head[from];head[from]=tt;
a[++tt].to=from;a[tt].dis=0;a[tt].cost=-cost;a[tt].nex=head[to];head[to]=tt;
}
bool vis[maxn];
ll costs[maxn];
bool spfa(){
memset(vis,0,sizeof(vis));
memset(costs,0x3f,sizeof(costs));
queue<int> q;
vis[s]=1;
q.push(s);
costs[s]=0;
while(!q.empty()){
ll top=q.front();
q.pop();
vis[top]=0;
for(ll i=head[top];i;i=a[i].nex){
if(costs[top]+a[i].cost<costs[a[i].to]&&a[i].dis){
costs[a[i].to]=costs[top]+a[i].cost;
if(!vis[a[i].to]){
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
if(costs[t]==costs[0]){
return 0;
}
return 1;
}
ll ans=0,anscost=0;
ll dfs(ll x,ll minn){
if(x==t){
vis[t]=1;
ans+=minn;
return minn;
}
int use=0;
vis[x]=1;
for(ll i=head[x];i;i=a[i].nex){
if((!vis[a[i].to]||a[i].to==t)&&costs[a[i].to]==costs[x]+a[i].cost&&a[i].dis){
ll search=dfs(a[i].to,min(minn-use,a[i].dis));
if(search>0){
use+=search;
anscost+=(a[i].cost*search);
a[i].dis-=search;
a[i^1].dis+=search;
if(use==minn){
break;
}
}
}
}
return use;
}
void dinic(){
while(spfa()){
do{
memset(vis,0,sizeof(vis));
dfs(s,inf);
}while(vis[t]);
}
printf("%lld",-anscost);
}
ll dis(ll xx1,ll yy1,ll xx2,ll yy2){
return floor((double)sqrt((ll)(xx1-xx2)*(xx1-xx2)+(yy1-yy2)*(yy1-yy2)));
}
int main(){
scanf("%lld%lld",&n,&k);
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld%lld",&xx1[i],&yy1[i],&xx2[i],&yy2[i]);
diss[i]=dis(xx1[i],yy1[i],xx2[i],yy2[i]);
xx1[i]*=2;
xx2[i]*=2;
if(xx1[i]==xx2[i]){
xx2[i]++;
}else{
xx1[i]++;
}
num[++cnt]=xx1[i];
num[++cnt]=xx2[i];
}
sort(num+1,num+1+cnt);
ll len=unique(num+1,num+1+cnt)-num-1;
t=len;
s=len+1;
add(s,1,k,0);
for(ll i=1;i<t;i++){
add(i,i+1,k,0);
}
for(ll i=1;i<=n;i++){
add(lower_bound(num+1,num+1+len,xx1[i])-num,lower_bound(num+1,num+1+len,xx2[i])-num,1,-1*diss[i]);
}
dinic();
return 0;
}
/*
4 2
-1 0 0 3
-1 1 0 2
-1 2 0 1
1 1 2 2
*/
P1251 \(\color{#9D3DCF}{餐巾计划问题}\)
题目大意
一个餐厅在接下去的\(N\)天中每天需要\(r_i\)块餐巾,每天餐巾来源有以下几种,求满足每天餐巾需求的总花费的最小值:
- 早上花\(p\)元买一块餐巾;
- 晚上花\(m\)天\(f\)元快洗一块餐巾;
- 晚上花\(n\)天\(s\)元慢洗一块餐巾。(\(n>m,s<f\))
思路
考虑每天的早晚各有操作,我们把一天拆成早晚两个点考虑(表示第\(i\)天早上的点编号为\(i\),晚上的为\(i+N\)):
- 若第\(i\)天早上要买餐巾,则\(s\)向\(i\)连\(f=\infty,c=p\)的边,表示花费\(p\)可以无限购入餐巾;
- 若第\(i\)天晚上要快洗餐巾,则\(i+N\)向\(i+m\)连\(f=\infty,c=f\)的边,表示可以给\(m\)天后的早上花\(f\)元提供餐巾;
- 若第\(i\)天晚上要慢洗餐巾,则\(i+N\)向\(i+n\)连\(f=\infty,c=s\)的边,表示可以给\(n\)天后的早上花\(s\)元提供餐巾;
- 若第\(i\)天晚上有餐巾不洗留着,则\(i+N\)向\(i+1+N\)连\(f=\infty,c=0\)的边,表示免费把今天晚上的脏餐巾留到明天晚上。
现在考虑如何保证每天早上的餐巾量满足需求:
我们将\(s\)与每天开始相连,\(f=r_i,c=0\),表示\(i\)必须要有\(r_i\)的餐巾,而每天的脏餐巾可以由\(s\)向\(i+N\)免费提供,即连\(f=r_i,c=0\)的边。
综上,跑最小费用最大流即可。
细节
- 注意是开始点与\(t\)连(确保每天餐巾满足),\(s\)与结束点连(提供脏餐巾)而不是直觉的\(s\)与早上、晚上与\(t\)连,否则手推会发现答案不对且无法合理解释(无法确保早上有足够餐巾)。
代码
点击查看代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 5005
#define maxm 50005
#define ll long long
#define inf 0x3fffffff
using namespace std;
int n,need[maxn],p,m,f,nin,sin,s,t;
int head[maxn],tt=1;
struct node{
int to,dis,cost,nex;
}a[maxm*2];
void add(int from,int to,int dis,int cost){
a[++tt].to=to;a[tt].dis=dis;a[tt].cost=cost;a[tt].nex=head[from];head[from]=tt;
a[++tt].to=from;a[tt].dis=0;a[tt].cost=-cost;a[tt].nex=head[to];head[to]=tt;
}
bool vis[maxn];
int costs[maxn];
bool spfa(){
memset(vis,0,sizeof(vis));
memset(costs,0x3f,sizeof(costs));
queue<int> q;
vis[s]=1;
q.push(s);
costs[s]=0;
while(!q.empty()){
int top=q.front();
q.pop();
vis[top]=0;
for(int i=head[top];i;i=a[i].nex){
if(costs[top]+a[i].cost<costs[a[i].to]&&a[i].dis){
costs[a[i].to]=costs[top]+a[i].cost;
if(!vis[a[i].to]){
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
if(costs[t]==costs[0]){
return 0;
}
return 1;
}
ll ans=0,anscost=0;
int dfs(int x,int minn){
if(x==t){
vis[t]=1;
ans+=minn;
return minn;
}
int use=0;
vis[x]=1;
for(int i=head[x];i;i=a[i].nex){
if((!vis[a[i].to]||a[i].to==t)&&costs[a[i].to]==costs[x]+a[i].cost&&a[i].dis){
int search=dfs(a[i].to,min(minn-use,a[i].dis));
if(search>0){
use+=search;
anscost+=(a[i].cost*search);
a[i].dis-=search;
a[i^1].dis+=search;
if(use==minn){
break;
}
}
}
}
return use;
}
void dinic(){
while(spfa()){
do{
memset(vis,0,sizeof(vis));
dfs(s,inf);
}while(vis[t]);
}
printf("%lld",anscost);
}
int main(){
scanf("%d",&n);
s=2*n+1;
t=s+1;
for(int i=1;i<=n;i++){
scanf("%d",&need[i]);
add(s,i+n,need[i],0);
add(i,t,need[i],0);
}
scanf("%d%d%d%d%d",&p,&m,&f,&sin,&nin);
for(int i=1;i<=n;i++){
add(s,i,need[i],p);
if(i+1<=n) add(i+n,i+1+n,inf,0);
if(i+m<=n) add(i+n,i+m,inf,f);
if(i+sin<=n) add(i+n,i+sin,inf,nin);
}
dinic();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号