网络流
网络流
网络流(network-flows)是一种类比水流的解决问题方法,与线性规划密切相关。网络流的理论和应用在不断发展,出现了具有增益的流、多终端流、多商品流以及网络流的分解与合成等新课题。网络流的应用已遍及通讯、运输、电力、工程规划、任务分派、设备更新以及计算机辅助设计等众多领域。
最大流#
定义#
管道网络中每条边的最大通过能力(容量)是有限的,实际流量不超过容量。
最大流问题(),一种组合最优化问题,就是要讨论如何充分利用装置的能力,使得运输的流量最大,以取得最好的效果。求最大流的标号算法最早由福特和福克逊于1956年提出,20世纪50年代福特()、福克逊()建立的“网络流理论”,是网络应用的重要组成成分。
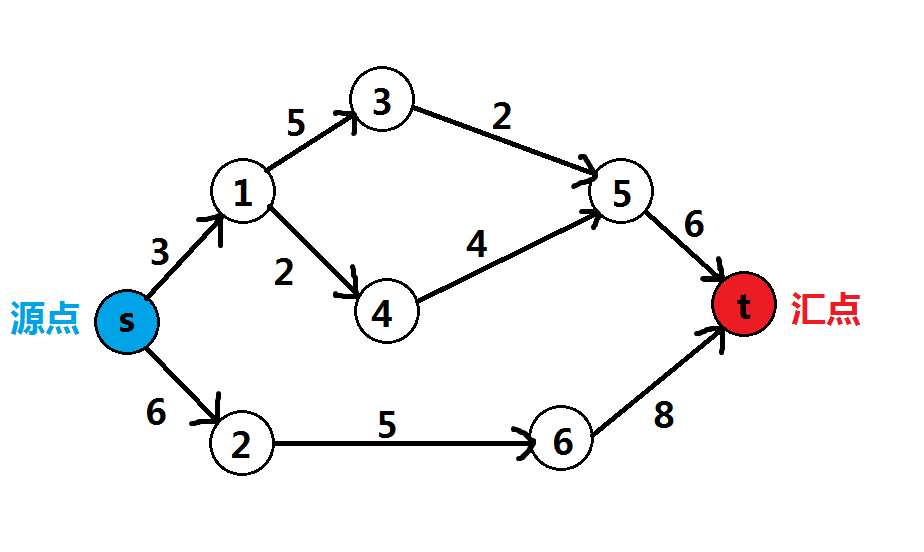
说得通俗点,可以把这幅图看作是自来水厂的供水路线:点是自来水厂,有个单位的水源源不断地向外输出,但是,到了点。即住户家里水量却是有限的。这是因为每条水管的容量有限,才导致水的流量也是有限的,且满足流量容量。回到图中,“自来水厂”点称作源点,“住户家”点称为汇点,“容量”即为边的边权。
你想让到你家的水尽量多,所以就衍生出了最大流的问题:即从源点有无限多的水输出,严格满足流量容量时,能够到达汇点的最大流量为多少?
为了解决这个问题,我们首先分析一下每条边的权值是如何影响这条路径的流量的:
如下图图,显然最大流为,因为尽管的容量为,可以通过最大为的水流,但是的容量只有,最多只能容纳个单位的水流过。
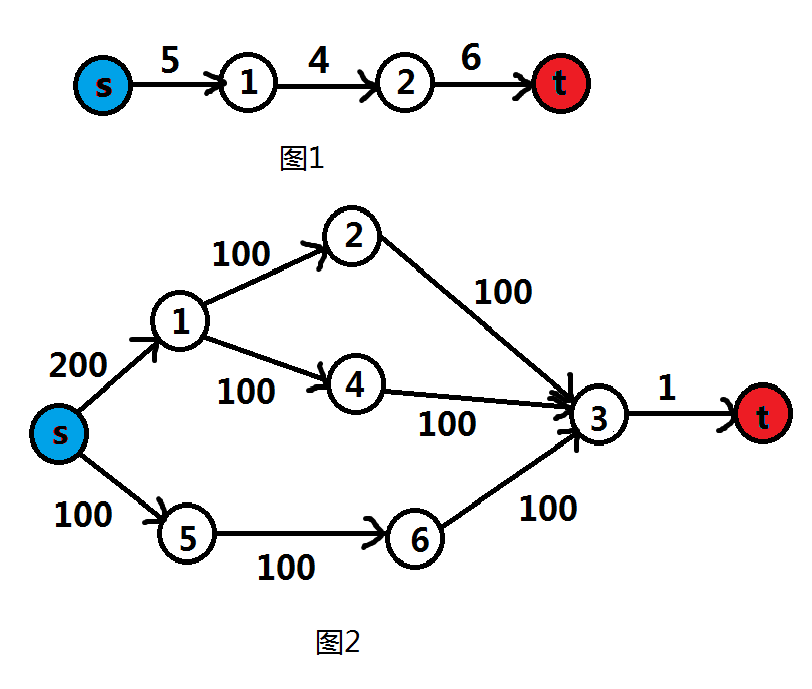
如图,尽管其它节点的容量很大,但是的容量只有,所以最大流为。
所以,某条路径上的最大流量取决于整条路上容量的最小值,即一条路径{…}的最大流。
求最大流的算法#
EK(Edmond—Karp)算法#
首先引入增广路的概念:
- 增广路
增广路指从到的一条路,水流流过这条路,使得当前可以到达的流量可以增加。
通过定义,我们显然可以看出求最大流其实就是不断寻找增广路的过程。直到找不到增广路时,到汇点的流量即为最大流。
那么,如何不断寻找增广路呢?爆搜!(其实就是不断),从到进行广搜,搜索一条增广路,将这条路的流量和答案都加上,即整条路径的最小容量。但是,为了减少变量(其实就是太懒),我们完全可以用当前路径的所有边的容量减去代替将每条边的流量增加即可,即得到的结果为该边还能容纳多大的水流,也就是剩下的容量。所以,的时候只要不断地找所有边权均的边即可。等到找不到增广路的时候,我们得到的答案就是最大流了。
但是,这个结论似乎有一点不对劲?
如图,此时如果,计算机很可能找到的是的增广路(如图中橙色路径),并将其权值都减掉,得到图。此时找不到任何增广路了,于是程序结束,最后得到的最大流为。但是,显然如果是和两条路的话,得到的最大流应该是。换句话说,我们目前的程序有一个问题:直接找增广路并操作得到的并不一定是最大流。
针对这个问题,我们可以引入图的反向边来解决。如图,在建图时加入反向边,且权值为,方向与原边相反:
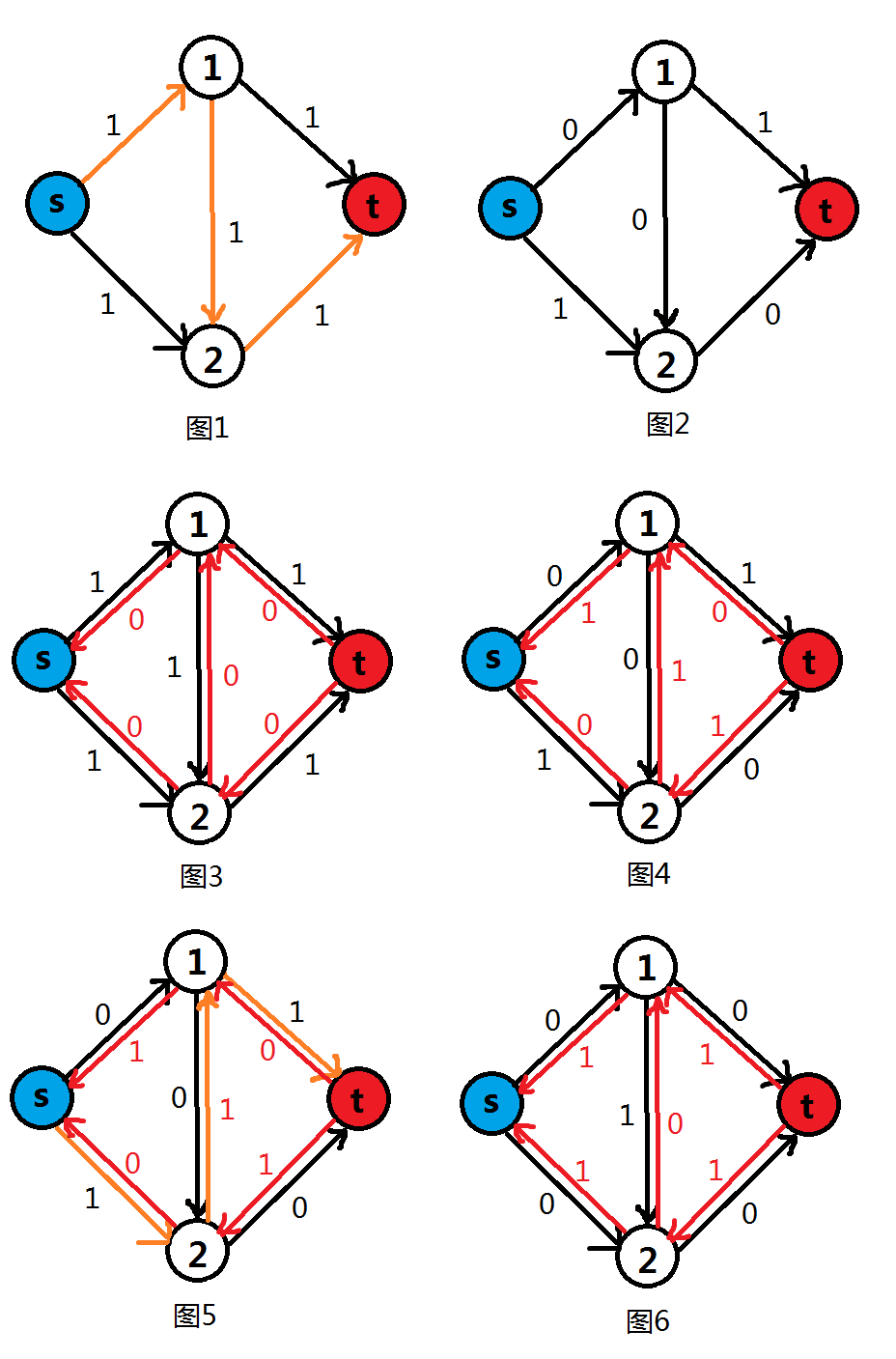
当有反向边存在后,找到增广路后将权值减少后,将反向边的权值加(如图)。然后继续,反向边也算进去,就会找到如图橙色部分所示的一条增广路。再找到最小容量,同样操作后得到图。这时我们发现:现在的图和通过我们之前说的和两条路之后的结果一样。所以我们可以得出反向边的用途:
。
也可以理解成,反向边的作用是(以上述例子解释):当有更好情况但是已经被前面搜到的增广路占用时(上述例子中为),利用反向边退给的流量,即有的流量不往和流而改往流,因为我们搜第二条增广路时将的容量也减了,也就是流量增加了。这样就给想往流的流量留出了位置,于是就会有的流量往流,而的流量相当于减了又加了,相当于不变。
- 代码
以 P3376 【模板】网络最大流 为例
- 建图
建图的方法很多,我比较喜欢采用邻接表(链式前向星)存储:
struct node{//结构体
int to,dis,nex;
//to:边指向的节点 dis:权值/容量 nex:同起点的下一条边的下标
}a[maxm*2];
int head[maxn],num=1;
//head[i]表示以i为起点的第一条边在a中的下标,num记录a中最大下标(总边数)
void add(int from,int to,int dis){//增加一条边
a[++num].to=to;
a[num].dis=dis;
a[num].nex=head[from];
head[from]=num;
}
- 找增广路
从源点开始,搜每个节点,当且仅当边权(即容量)时进入,到达汇点时即为一条增广路。
bool bfs(){
queue<int> q;//队列
memset(vis,0,sizeof(vis));
vis[s]=1;//是否搜过
q.push(s);
while(!q.empty()){
int top=q.front();//队首
q.pop();
for(int i=head[top];i;i=a[i].nex){//搜所有从top开始的边
if(!vis[a[i].to]&&a[i].dis){//若没去过且容量大于0
vis[a[i].to]=1;//标记去过
p[a[i].to].pre=top;//记录路径,pre为上一个点
p[a[i].to].edge=i;//记录路径,edge为边
if(a[i].to==t){//到汇点返回1,表示有增广路
return 1;
}
q.push(a[i].to);
}
}
}
return 0;//若全部搜完还没有出现增广路,返回0
}
- 算法核心
不断搜增广路,更新权值。搜不到增广路时答案即为最大流。
- 特别注意,代码中将下标异或后得到的即为其反向边。因为建边时边和其反向边总是成对出现且反向边为奇数。
void ek(){
long long ans=0;
while(bfs()){//不断找增广路
int minn=99999999;
for(int i=t;i!=s;i=p[i].pre){
minn=min(minn,a[p[i].edge].dis);//找最小容量
}
for(int i=t;i!=s;i=p[i].pre){//更改
a[p[i].edge].dis-=minn;
a[p[i].edge^1].dis+=minn;
}
ans+=minn;
}
printf("%lld",ans);//输出最大流
}
- 完整代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 210
#define maxm 5005
using namespace std;
int n,m,s,t,u,v,w;
struct node{
int to,dis,nex;
}a[maxm*2];
int head[maxn],num=1;
void add(int from,int to,int dis){
a[++num].to=to;
a[num].dis=dis;
a[num].nex=head[from];
head[from]=num;
}
bool vis[maxn];
struct path{
int pre,edge;
}p[maxm*2];
bool bfs(){
queue<int> q;
memset(vis,0,sizeof(vis));
vis[s]=1;
q.push(s);
while(!q.empty()){
int top=q.front();
q.pop();
for(int i=head[top];i;i=a[i].nex){
if(!vis[a[i].to]&&a[i].dis){
vis[a[i].to]=1;
p[a[i].to].pre=top;
p[a[i].to].edge=i;
if(a[i].to==t){
return 1;
}
q.push(a[i].to);
}
}
}
return 0;
}
void ek(){
long long ans=0;
while(bfs()){
int minn=99999999;
for(int i=t;i!=s;i=p[i].pre){
minn=min(minn,a[p[i].edge].dis);
}
for(int i=t;i!=s;i=p[i].pre){
a[p[i].edge].dis-=minn;
a[p[i].edge^1].dis+=minn;
}
ans+=minn;
}
printf("%lld",ans);
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,0);
}
ek();
return 0;
}
Dinic算法#
Dinic算法(又称Dinitz算法)是一个在网络流中计算最大流的强多项式复杂度的算法,设想由以色列(前苏联)的计算机科学家Yefim (Chaim) A. Dinitz在1970年提出。
让我们优化一下算法。
注意到,中,我们是一条一条地搜增广路,那么,可不可以一次搜出所有(或多条)增广路呢?于是,算法解决了需要多路增广的问题。
算法的过程如下:
- 将图分层;
- 搜出所有增广路;
- 重复前两步,直到找不到增广路为止。
首先看到第一步,分层有什么用呢?实际上,分层是为了让我们找到的增广路是最短的,如图(分的层用红色数字标在节点旁边),我们就会搜的增广路而不是另一条更长的路了。
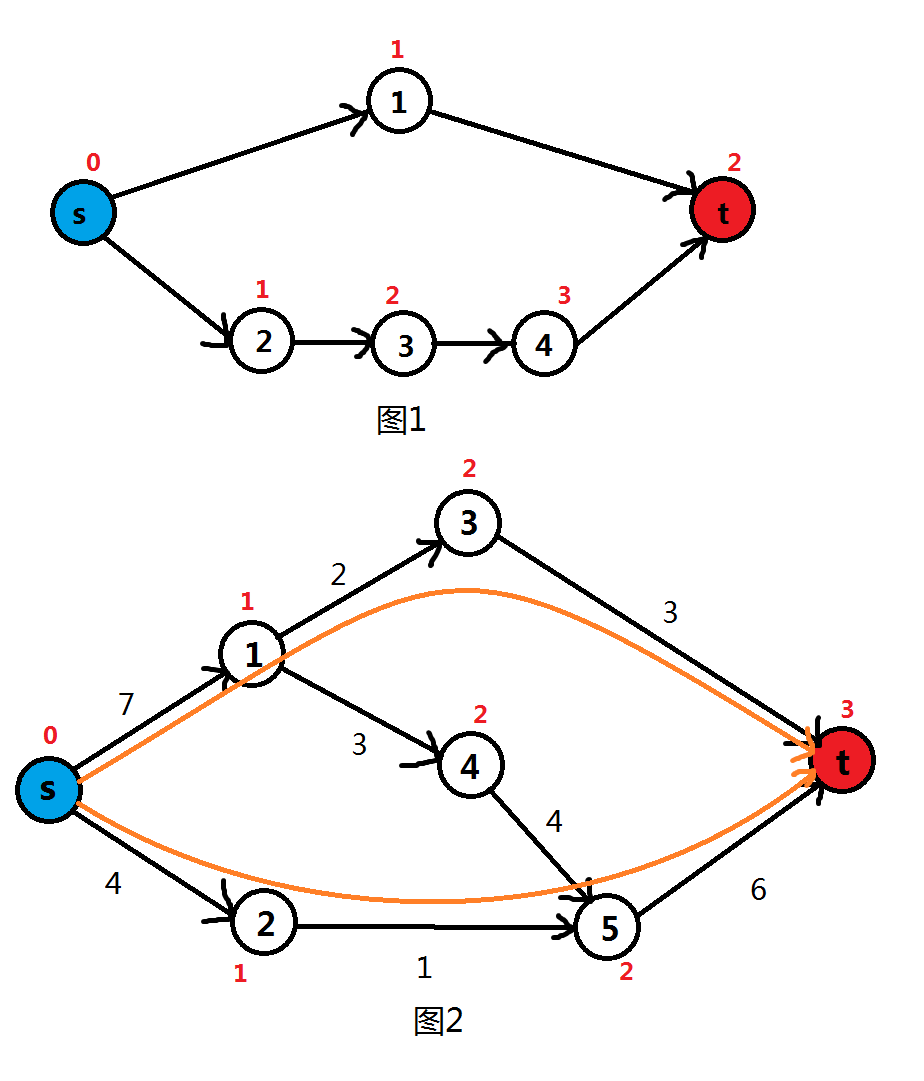
分完层后,我们就进行到第步搜增广路了。用看似时间更长,实际上它在时间变化不大的同时还能搜到所有增广路。如图,分完层后,用搜出的两条路径如图中橙色部分。进行完后和一样减容量、加反向边容量,再继续分层、搜索……直到没有增广路(即所有边都到不了汇点)即可结束。具体看代码解析。
- 代码(例题还是一样的)
- 分层
时,先将源点的层数设为(其实也没什么关系),之后广搜,找到能更新的边就更新。
bool bfs(){
memset(dep,0x3f,sizeof(dep));//层数
memset(vis,0,sizeof(vis));//是否入过队
queue<int> q;
dep[s]=0;
q.push(s);
vis[s]=1;
while(!q.empty()){
int top=q.front();
q.pop();
for(int i=head[top];i;i=a[i].nex){
if(dep[a[i].to]>dep[top]+1&&a[i].dis){//可更新的就更新
dep[a[i].to]=dep[top]+1;
if(!vis[a[i].to]){//没入过队的入队
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
if(dep[t]==dep[0]){//若汇点t的层数和0号节点一样,即为初始值,意味着没有增广路了,返回false
return 0;
}
return 1;
}
- 搜索
用表示这条路的最大容量(其实就是上面介绍时的),表示用过的容量。的主要作用是,记录当前搜过的增广路要减去的流量,当的值等于时,意味着当前的边已经达到了最大容量,此时停止搜索。
ll dfs(int x,int minn){//x为当前节点编号
if(x==t){//到达汇点
ans+=minn;//累加答案
return minn;
}
int use=0;
for(int i=head[x];i;i=a[i].nex){
if(a[i].dis&&dep[a[i].to]==dep[x]+1){//满足最短增广路且还有剩余容量
int nex=dfs(a[i].to,min(minn-use,a[i].dis));//向下搜
if(nex>0){//若结果大于0,说明有增广路,因为若下面没有增广路了则会返回use的初值0
use+=nex;//增加当前流量
a[i].dis-=nex;
a[i^1].dis+=nex;
if(use==minn){//达到最大容量
break;
}
}
}
}
return use;
}
- 算法核心
非常简洁,因为主要部分都在两个搜索里了。
void dinic(){
while(bfs()){//若有增广路
dfs(s,99999999);//搜索(minn的初值大一点就好)
}
printf("%lld",ans);//搜完输出答案
}
- 完整代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 210
#define maxm 5005
#define ll long long
using namespace std;
int n,m,s,t,u,v,w;
ll ans=0;
struct node{
int to,dis,nex;
}a[maxm*2];
int head[maxn],num=1;
void add(int from,int to,int dis){
a[++num].to=to;
a[num].dis=dis;
a[num].nex=head[from];
head[from]=num;
}
bool vis[maxn];
int dep[maxn];
bool bfs(){
memset(dep,0x3f,sizeof(dep));
memset(vis,0,sizeof(vis));
queue<int> q;
dep[s]=0;
q.push(s);
vis[s]=1;
while(!q.empty()){
int top=q.front();
q.pop();
for(int i=head[top];i;i=a[i].nex){
if(dep[a[i].to]>dep[top]+1&&a[i].dis){
dep[a[i].to]=dep[top]+1;
if(!vis[a[i].to]){
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
if(dep[t]==dep[0]){
return 0;
}
return 1;
}
ll dfs(int x,int minn){
if(x==t){
ans+=minn;
return minn;
}
int use=0;
for(int i=head[x];i;i=a[i].nex){
if(a[i].dis&&dep[a[i].to]==dep[x]+1){
int nex=dfs(a[i].to,min(minn-use,a[i].dis));
if(nex>0){
use+=nex;
a[i].dis-=nex;
a[i^1].dis+=nex;
if(use==minn){
break;
}
}
}
}
return use;
}
void dinic(){
while(bfs()){
dfs(s,99999999);
}
printf("%lld",ans);
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,0);
}
dinic();
return 0;
}
但是,洛谷上却了一个点,时间达到了惊人的。此时,我们就要进行传说中的当前弧优化了。
Dinic算法+当前弧优化#
当前弧优化实际上只是增加了一个数组,用代替邻接表中的。
原理是:当我们已经搜过一条边时,一定已经让这条边无法继续增广了,所以这条边已经没什么用了,直接用记录下一条有用的边,搜索时就可以省时间了。
- 代码(最终版本)
刚才TLE的点直接减到了13ms
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 205
#define maxm 5005
#define ll long long
#define inf 0x3fffffff
using namespace std;
int n,m,s,t,u,v,w;
int head[maxn],tt=1;
struct node{
int to,dis,nex;
}a[maxm*2];
void add(int from,int to,int dis){
a[++tt].to=to;
a[tt].dis=dis;
a[tt].nex=head[from];
head[from]=tt;
}
bool vis[maxn];
int dep[maxn],cur[maxn];
bool bfs(){
for(int i=0;i<=n;i++){
vis[i]=0;
dep[i]=inf;
cur[i]=head[i];
}
queue<int> q;
vis[s]=1;
q.push(s);
dep[s]=0;
while(!q.empty()){
int top=q.front();
q.pop();
for(int i=head[top];i;i=a[i].nex){
if(dep[top]+1<dep[a[i].to]&&a[i].dis){
dep[a[i].to]=dep[top]+1;
if(!vis[a[i].to]){
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
if(dep[t]==dep[0]){
return 0;
}
return 1;
}
ll ans=0;
int dfs(int x,int minn){
if(x==t){
ans+=minn;
return minn;
}
int use=0;
for(int i=cur[x];i;i=a[i].nex){
cur[x]=i;
if(dep[a[i].to]==dep[x]+1&&a[i].dis){
int search=dfs(a[i].to,min(minn-use,a[i].dis));
if(search>0){
use+=search;
a[i].dis-=search;
a[i^1].dis+=search;
if(use==minn){
break;
}
}
}
}
return use;
}
void dinic(){
while(bfs()){
dfs(s,inf);
}
printf("%lld",ans);
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w);
add(v,u,0);
}
dinic();
return 0;
}
最小割#
定义#
对于一个网络流图,其割的定义为一种点的划分方式:将所有的点划分为和两个集合,且,其中源点,汇点。
定义割的容量(或)表示所有从到的边的容量之和,即。
最小割就是求得一个割使得最小。
也就是说,一个割就是:把图的所有节点分成两部分,割的容量就是所有从源点所在的点集到另一个点集的边的容量之和。如图为一些割及其容量。
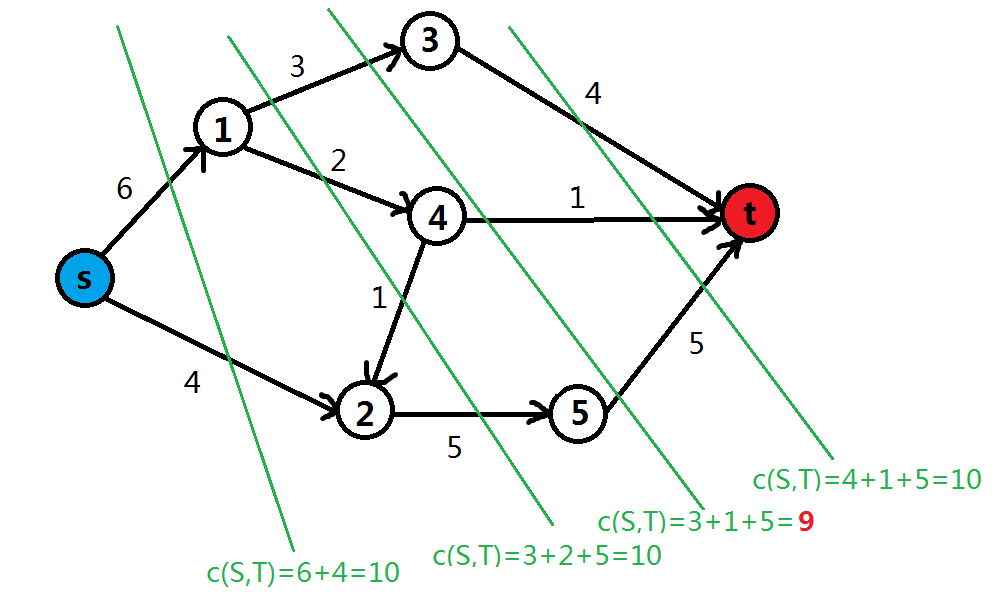
如图绿色线为四种割,其中第三条为最小割,为(标红部分)。
注意到,这幅图的最大流也是。那么,最大流与最小割有什么关系呢?
最大流最小割定理#
定理内容#
- 如果是网络中的一个流,是任意一个割,那么等于正向割边的流量与负向割边的流量之差。
- ,即最大流等于最小割。
证明#
- 设两点集分别为和,定义表示从指向的边的容量和(其实就是割的容量)。则只需证明即可。
显然若,则,。
那么若有一个节点:
若为源点,则;
若不是源点,则。
因为点集中所有点都满足上述关系式,相加得到。用①式得到:
- 由得到,对于每一个可行的流和一个割,我们可以得到。
特别地,当为最大流时,原图中一定没有增广路,即的出边一定满流,入边一定零流,即。
由以上两个式子得到此时一定最大,一定最小。即此时为最大流,为最小割,最大流等于最小割。
代码#
根据最大流最小割定理,用求出最大流即为最小割。
费用流—最小费用最大流#
定义#
给定网络,每条边除了有容量限制,还有一个单位流量的费用。
当(u,v)的流量为时,需要花费的费用。
则该网络中总花费最小的最大流称为最小费用最大流,即在最大化的前提下最小化。
那么,在有了费用(即每条边流过要缴的水费时),应该如何让流量最大且费用最少呢?
和一样,我们要分层、搜增广路并更新。那么,我们应该更改哪一步呢?
显然是分层,我们可以把改成已经凉了的,这样,就可以完成了。
代码#
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 5005
#define maxm 50005
#define ll long long
#define inf 0x3fffffff
using namespace std;
int n,m,s,t,u,v,w,cost;
int head[maxn],tt=1;
struct node{
int to,dis,cost,nex;
}a[maxm*2];
void add(int from,int to,int dis,int cost){
a[++tt].to=to;a[tt].dis=dis;a[tt].cost=cost;a[tt].nex=head[from];head[from]=tt;
a[++tt].to=from;a[tt].dis=0;a[tt].cost=-cost;a[tt].nex=head[to];head[to]=tt;
}
bool vis[maxn];
int costs[maxn];
bool spfa(){
memset(vis,0,sizeof(vis));
memset(costs,0x3f,sizeof(costs));
queue<int> q;
vis[s]=1;
q.push(s);
costs[s]=0;
while(!q.empty()){
int top=q.front();
q.pop();
vis[top]=0;
for(int i=head[top];i;i=a[i].nex){
if(costs[top]+a[i].cost<costs[a[i].to]&&a[i].dis){
costs[a[i].to]=costs[top]+a[i].cost;
if(!vis[a[i].to]){
vis[a[i].to]=1;
q.push(a[i].to);
}
}
}
}
if(costs[t]==costs[0]){
return 0;
}
return 1;
}
ll ans=0,anscost=0;
int dfs(int x,int minn){
if(x==t){
vis[t]=1;
ans+=minn;
return minn;
}
int use=0;
vis[x]=1;
for(int i=head[x];i;i=a[i].nex){
if((!vis[a[i].to]||a[i].to==t)&&costs[a[i].to]==costs[x]+a[i].cost&&a[i].dis){
int search=dfs(a[i].to,min(minn-use,a[i].dis));
if(search>0){
use+=search;
anscost+=(a[i].cost*search);
a[i].dis-=search;
a[i^1].dis+=search;
if(use==minn){
break;
}
}
}
}
return use;
}
void dinic(){
while(spfa()){
do{
memset(vis,0,sizeof(vis));
dfs(s,inf);
}while(vis[t]);
}
printf("%lld %lld",ans,anscost);
}
int main(){
scanf("%d%d%d%d",&n,&m,&s,&t);
for(int i=1;i<=m;i++){
scanf("%d%d%d%d",&u,&v,&w,&cost);
add(u,v,w,cost);
}
dinic();
return 0;
}



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 一个奇形怪状的面试题:Bean中的CHM要不要加volatile?
· [.NET]调用本地 Deepseek 模型
· 一个费力不讨好的项目,让我损失了近一半的绩效!
· .NET Core 托管堆内存泄露/CPU异常的常见思路
· PostgreSQL 和 SQL Server 在统计信息维护中的关键差异
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· DeepSeek “源神”启动!「GitHub 热点速览」
· 我与微信审核的“相爱相杀”看个人小程序副业
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库
· 上周热点回顾(2.17-2.23)