图的实现(邻接矩阵)及DFS、BFS

@author QYX

写作时间:2013/0302 最近准备noi比赛，加油!!!

因为近期学习任务太多太紧，所以我主要维护Github，博客园可能会停更几天。----2020年2月9日

图

 图（graph）是用线连接在一起的顶点或节点的集合，即两个要素：边和顶点。每一条边连接个两个顶点，用（i，j）表示顶点为 i 和 j 的边。

​ 如果用图示来表示一个图，一般用圆圈表示顶点，线段表示边。有方向的边称为有向边，对应的图成为有向图，没有方向的边称为无向边，对应的图叫无向图。对于无向图，边（i， j）和（j，i）是一样的，称顶点 i 和 j 是邻接的，边（i，j）关联于顶点 i 和 j ；对于有向图，边（i，j）表示由顶点 i 指向顶点 j 的边，即称顶点 i 邻接至顶点 j ，顶点 i 邻接于顶点 j ，边（i，j）关联至顶点 j 而关联于顶点 i 。

​ 对于很多的实际问题，不同顶点之间的边的权值（长度、重量、成本、价值等实际意义）是不一样的，所以这样的图被称为加权图，反之边没有权值的图称为无权图。所以，图分为四种：加权有向图，加权无向图，无权有向图，无权无向图。

 

图的表现有很多种，邻接表法，临接矩阵等。

图经常是以这种形式出现的[weight,from,to]的n*3维数组出现的,见名知意，三个元素分别为边的权重，从哪儿来，到哪儿去。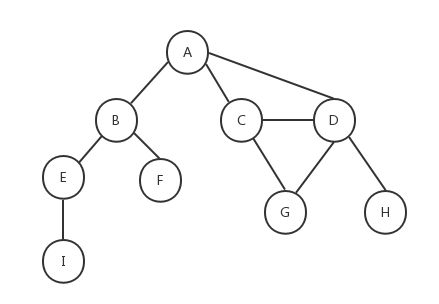

 

 如上图所示，由一条边连接在一起的顶点称为相邻顶点，A和B是相邻顶点，A和D是相邻顶点，A和C是相邻顶点......A和E是不相邻顶点。一个顶点的度是其相邻顶点的数量，A和其它三个顶点相连，所以A的度为3，E和其它两个顶点相连，所以E的度为2......路径是一组相邻顶点的连续序列，如上图中包含路径ABEI、路径ACDG、路径ABE、路径ACDH等。简单路径要求路径中不包含有重复的顶点，如果将环的最后一个顶点去掉，它也是一个简单路径。例如路径ADCA是一个环，它不是一个简单路径，如果将路径中的最后一个顶点A去掉，那么它就是一个简单路径。如果图中不存在环，则称该图是无环的。如果图中任何两个顶点间都存在路径，则该图是连通的，如上图就是一个连通图。如果图的边没有方向，则该图是无向图，上图所示为无向图，反之则称为有向图，下图所示为有向图：

 

 

　在有向图中，如果两个顶点间在双向上都存在路径，则称这两个顶点是强连通的，如上图中C和D是强连通的，而A和B是非强连通的。如果有向图中的任何两个顶点间在双向上都存在路径，则该有向图是强连通的，非强连通的图也称为稀疏图。

　　此外，图还可以是加权的。前面我们看到的图都是未加权的，下图为一个加权的图：

 

 

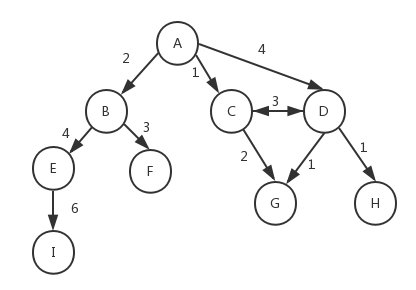
可以想象一下，前面我们介绍的树和链表也属于图的一种特殊形式。图在计算机科学中的应用十分广泛，例如我们可以搜索图中的一个特定顶点或一条特定的边，或者寻找两个顶点间的路径以及最短路径，检测图中是否存在环等等。

　　存在多种不同的方式来实现图的数据结构，下面介绍几种常用的方式。

邻接矩阵

　　在邻接矩阵中，我们用一个二维数组来表示图中顶点之间的连接，如果两个顶点之间存在连接，则这两个顶点对应的二维数组下标的元素的值为1，否则为0。下图是用邻接矩阵方式表示的图：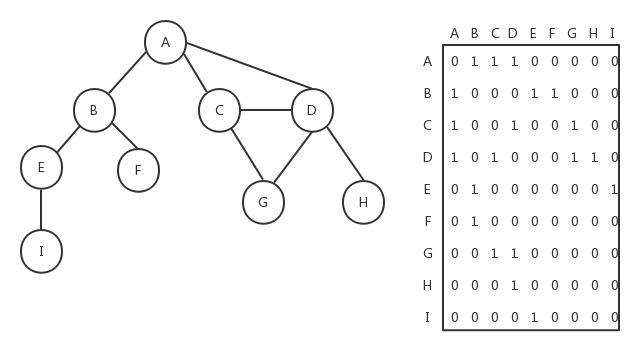

 

 

　如果是加权的图，我们可以将邻接矩阵中二维数组里的值1改成对应的加权数。邻接矩阵方式存在一个缺点，如果图是非强连通的，则二维数组中会有很多的0，这表示我们使用了很多的存储空间来表示根本不存在的边。另一个缺点就是当图的顶点发生改变时，对于二维数组的修改会变得不太灵活。

邻接表

　　图的另外一种实现方式是邻接表，它是对邻接矩阵的一种改进。邻接表由图中每个顶点的相邻顶点列表所组成。如下图所示，我们可以用数组、链表、字典或散列表来表示邻接表。

 

 

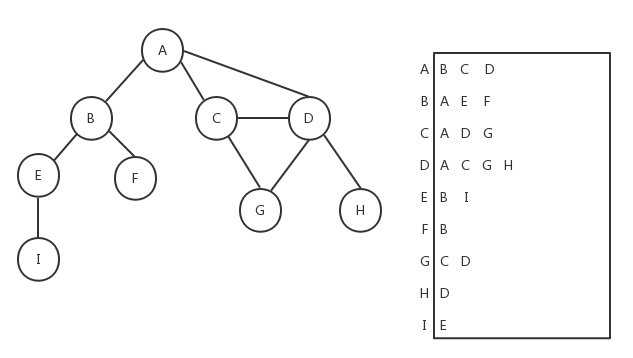
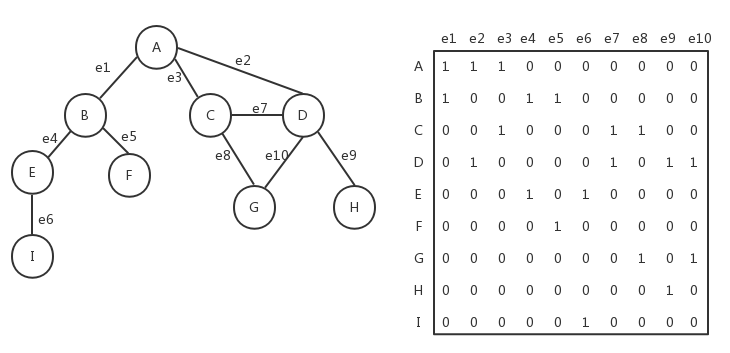
关联矩阵

　　我们还可以用关联矩阵来表示图。在关联矩阵中，矩阵的行表示顶点，列表示边。关联矩阵通常用于边的数量比顶点多的情况下，以节省存储空间。如下图所示为关联矩阵方式表示的图：

 

 

深度优先搜索#

深度优先搜索，我们以无向图为例。

图的深度优先搜索(Depth First Search)，和树的先序遍历比较类似。

它的思想：假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

显然，深度优先搜索是一个递归的过程。

广度优先搜索#

广度优先搜索，我们以有向图为例。

广度优先搜索算法(Breadth First Search)，又称为”宽度优先搜索”或”横向优先搜索”，简称BFS。

它的思想是：从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。

换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有路径相通且路径长度为1,2…的顶点。

package com.qyx;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
//使用邻接矩阵来实现图
public class Graph {
    private ArrayList<String> vertexList; //存储顶点的集合
    private int[][] edges;//存储图对应的邻接矩阵
    private int numOfEdges;//表示边的数目
    private boolean isVisited[];
    public static void main(String[] args) {
        int n=5;//节点的个数
        String vertex[]={"A","B","C","D","E"};
        //创建图对象
        Graph graph=new Graph(n);
        for (String s:vertex)
        {
            graph.vertexList.add(s);
        }
        //添加边
        graph.insertEdge(0,1,1);
        graph.insertEdge(0,2,1);
        graph.insertEdge(1,2,1);
        graph.insertEdge(1,3,1);
        graph.insertEdge(1,4,1);
        //显示邻接矩阵
        graph.showGraph();
        //graph.dfs();
        graph.bfs();
    }
    //构造器
    public Graph(int n)
    {
        //初始化邻接矩阵和vertexList
        edges=new int[n][n];
        vertexList=new ArrayList<String>();
        numOfEdges=0;
        isVisited=new boolean[5];
    }
    //插入顶点
    public void insertVertex(String vertex)
    {
        vertexList.add(vertex);
    }

    /**
     *
     * @param v1 表示点的下标 即是第几个顶点
     * @param v2 第二个顶点对应的下标
     * @param weight 表示是否连接 0不相连 1相连
     */
    //添加边
    public void insertEdge(int v1,int v2,int weight)
    {
        edges[v1][v2]=weight;
        edges[v2][v1]=weight;
        numOfEdges++;
    }
    //图中常用的方法
    //返回节点的个数
    public int getNumOfVertex()
    {
        return vertexList.size();
    }
    //得到边的数目
    public int getNumOfEdges()
    {
        return numOfEdges;
    }
    //返回节点i对应的值 0-A 1-B 2-C
    public String getValue(int index)
    {
        return vertexList.get(index);
    }
    //返回v1和v2的权值
    public int getWeight(int v1,int v2)
    {
        return edges[v1][v2];
    }
    //显示图对应的邻接矩阵
    public void showGraph()
    {
        for (int[] arrs:edges)
        {
            System.out.println(Arrays.toString(arrs));
        }
    }

    /**
     *
     * @param index
     * @return 如果存在返回对应的下标，否则返回-1
     */
    //得到第一个邻接节点的下标
    public int getFirstNeighbor(int index)
    {
        for (int j=index;j<vertexList.size();j++)
        {
            if (edges[index][j]>0)
            {
                return j;
            }
        }
        return -1;
    }
    //根据前一个邻接节点的下标来获取下一个邻接节点
    public int getNextNeighbor(int v1,int v2) {
        for (int i = v2 + 1; i < vertexList.size(); i++) {
                if (edges[v1][i] > 0) {
                    return i;
                }
        }
        return -1;
    }
        //深度优先遍历算法
        //i 第一次就是0
        private void dfs ( boolean[] isVisited, int i)
        {
            //首先我们访问该节点
            System.out.print(getValue(i) + "->");
            //将该邻接节点设置为已访问
            isVisited[i] = true;
            int w = getFirstNeighbor(i);//查找节点w的第一个邻接节点w
            while (w != -1) {
                if (!isVisited[w]) {
                    dfs(isVisited,w);
                }
                //如果已经被访问过
                w=getNextNeighbor(i,w);
            }
        }
    //对dfs进行重载，遍历所有的节点并进行dfs
    public void dfs()
    {
        //遍历所有的节点进行dfs
        for (int i=0;i<getNumOfVertex();i++)
        {
            if (!isVisited[i])
            {
                dfs(isVisited,i);
            }
        }
    }
    //对一个节点进行深度优先遍历的方法
    public void bfs(boolean[] isVisited,int i)
    {
        int u;//表示队列的头结点对应下标
        int w;//邻接节点
        //队列，记录节点访问的顺序
        LinkedList queue = new LinkedList();
        //访问节点
        System.out.print(getValue(i)+"->");
        //标记为已访问
        isVisited[i]=true;
        //将节点加入队列
        queue.addLast(i);
        while (!queue.isEmpty())
        {
            //取出队列的头结点下标
            u =(Integer)queue.removeFirst();
            //得到第一个邻接节点的下标w
            w =getFirstNeighbor(u);
            while (w!=-1)
            {
                //找到
                //是否访问
                if (!isVisited[w])
                {
                    System.out.print(getValue(w)+"->");
                    //入队
                    queue.addLast(w);
                    isVisited[w]=true;
                }
                //找w后面的下一个邻接节点
                w=getNextNeighbor(u,w); //体现出广度优先

            }
        }
    }
    //遍历所有的节点都进行广度优先搜索
    public void bfs()
    {
        for (int i=0;i<getNumOfVertex();i++)
        {
            if (!isVisited[i])
            {
                bfs(isVisited,i);
            }
        }
    }
}

 2020年2月9日对原有博客进行了修改,参考博客:

https://www.cnblogs.com/jaxu/p/11338294.html

 https://www.cnblogs.com/DarrenChan/p/9547869.html

感谢帮助!