赫夫曼编码
哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。
哈夫曼编码,主要目的是根据使用频率来最大化节省字符(编码)的存储空间。
哈夫曼编码的原理就是基于哈夫曼树
哈夫曼树相关的几个名词
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。图 1 中,从根结点到结点 a 之间的通路就是一条路径。
路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。图 1 中从根结点到结点 c 的路径长度为 3。
结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。例如,图 1 中结点 a 的权为 7,结点 b 的权为 5。
结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如,图 1 中结点 b 的带权路径长度为 2 * 5 = 10 。
树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如图 1 中所示的这颗树的带权路径长度为:
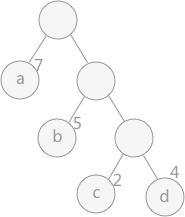
WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3
什么是哈夫曼树
当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为“最优二叉树”,有时也叫“赫夫曼树”或者“哈夫曼树”。
在构建哈弗曼树时,要使树的带权路径长度最小,只需要遵循一个原则,那就是:权重越大的结点离树根越近。在图 1 中,因为结点 a 的权值最大,所以理应直接作为根结点的孩子结点。
构建哈夫曼树
对于给定的有各自权值的 n 个结点,构建哈夫曼树有一个行之有效的办法:
第一步:我们创建节点类,这些值作为节点的权值,存储在集合里。

第二步:将这些节点按照权值的大小进行排序。

第三步:取出权值最小的两个节点,并创建一个新的节点作为这两个节点的父节点,这个父节点的权值为两个子节点的权值之和。将这两个节点分别赋给父节点的左右节点。
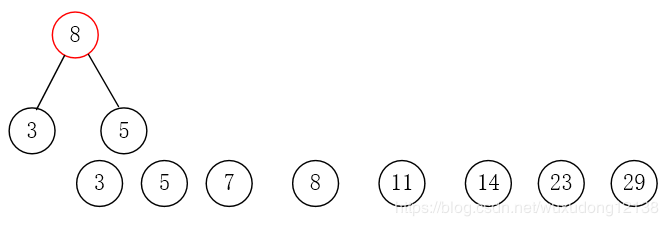
第四步:删除这两个节点,将父节点添加进集合里。
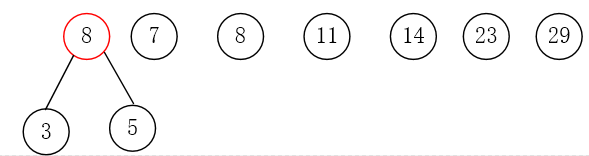
第五步:重复第二步到第四步,直到集合中只剩一个元素,结束循环。
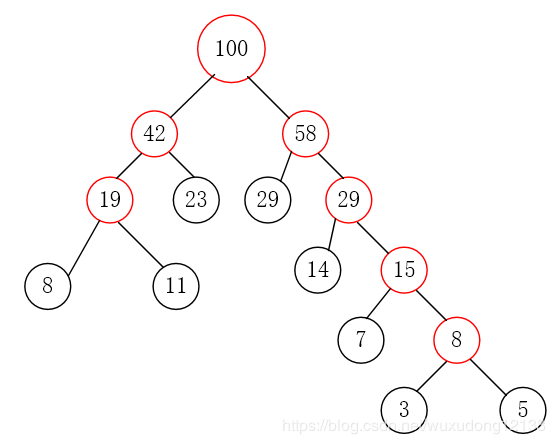
哈夫曼编码过程:
1 将字符串转换为byte数组
2 检查byte数组中字符的出现次数,将字符的byte和字符出现次数保存为节点,放入集合中
3 构建哈夫曼树
4 设左路径为0 右路径为1 计算字符的哈夫曼编码值,存入Map集合中
5 参照Map集合,将byte数组转换为byte字符串,将其对照Map集合逐一处理,由于数据量较大,所以八位一组进行数据压缩
package com.qyx; import java.lang.reflect.Array; import java.util.*; /** * 赫夫曼编码 */ public class HuffmanCode { public static void main(String[] args){ String str="i like java forever"; byte[] bytes=str.getBytes(); byte[] bys=huffmanZip(bytes); System.out.println(Arrays.toString(bys)); } private static List<Node> getNodes(byte[] bytes) { //1 创建ArrayList ArrayList<Node> list=new ArrayList<Node>(); //遍历bytes,统计存储每个byte出现的次数->map Map<Byte,Integer> counts=new HashMap<Byte, Integer>(); for(byte b:bytes) { Integer count=counts.get(b); if (count==null) { counts.put(b,1); }else { counts.put(b, count + 1); } } //把每个键值对转化成一个Node对象,并放入到nodes集合中 for (Map.Entry<Byte,Integer> entry:counts.entrySet()) { list.add(new Node(entry.getKey(),entry.getValue())); } return list; } //通过List创建对应的哈夫曼树 private static Node createHuffManTree(List<Node> list) { while (list.size()>1) { //排序,从小到大,根据我们实现的compareTo方法来决定的 Collections.sort(list); Node leftNode=list.get(0); Node rightNode=list.get(1); //新的根节点没有data,只有权值 Node parent=new Node(null,leftNode.weight+rightNode.weight); parent.left=leftNode; parent.right=rightNode; //将已经处理的两颗二叉树从list移除 list.remove(leftNode); list.remove(rightNode); list.add(parent); } return list.get(0); } //生成哈夫曼树对应的哈夫曼编码表 /** * 思路: * 1 将赫夫曼编码表存放在Map<Byte,String>中 * 2 在生成赫夫曼编码表示,需要去拼接路径,定义一个StringBuilder * 存储某个叶子节点的路径 * @param */ private static Map<Byte,String> huffmanCodes=new HashMap<Byte, String>(); private static StringBuilder builder=new StringBuilder(); /** * 功能:将传入的node结点的所有叶子节点的赫夫曼编码得到,并放入到huffmanCode的集合中 * @param node 传入节点 * @param code 路径:左子节点是0,右子节点是1 * @param builder 用于拼接路径 */ private static void getCodes(Node node,String code,StringBuilder builder) { StringBuilder builder1=new StringBuilder(builder); //将code加入到builder1 builder1.append(code); if (node!=null) { //判断当前node是叶子节点还是非叶子节点 if(node.data==null) { //非叶子节点,则需要递归 //向左递归 getCodes(node.left,"0",builder1); //向右递归 getCodes(node.right,"1",builder1); }else{ //说明是一个叶子节点 huffmanCodes.put(node.data,builder1.toString()); } } } //为了调用方便,重载getCodes private static Map<Byte,String> getCodes(Node root) { if (root==null) { return null; } //处理root的左子树 getCodes(root.left,"0",builder); //处理root的右子树 getCodes(root.right,"1",builder); return huffmanCodes; } //编写一个方法,将字符串对应的byte[]数组,通过生成的赫夫曼编码表,返回一个赫夫曼编码 压缩后的byte[] /** * * @param bytes 这是原始的字符串生成byte数组 * @param huffmanCodes 这是字符对应的赫夫曼编码的map * @return 返回赫夫曼编码处理后的字符数组 */ private static byte[] zip(byte[] bytes,Map<Byte,String>huffmanCodes) { //1 利用huffmanCodes将bytes转成转成赫夫曼编码对应的字符串 StringBuilder stringBuilder=new StringBuilder(); //遍历bytes数组 for(byte b:bytes) { stringBuilder.append(huffmanCodes.get(b)); } //System.out.println("测试stringBuilder="+stringBuilder.toString()); //将赫夫曼字符串转成byte[] int len; if (stringBuilder.length()%8==0) { len=stringBuilder.length()/8; }else { len=stringBuilder.length()/8+1; } //创建 存储压缩后的byte数组 byte[] by=new byte[len]; int index=0;//记录是第几个byte for (int i=0;i<stringBuilder.length();i+=8) { //因为是每8位对应一个byte,所有步长+8 String strByte; if (i+8>stringBuilder.length()) { //不够8位 strByte=stringBuilder.substring(i); }else { strByte = stringBuilder.substring(i, i + 8); } //将strByte转成byte数组,放入到by by[index]= (byte) Integer.parseInt(strByte,2); index++; } return by; } //使用一个方法,将前面的方法封装起来,便于调用 /** * * @param bytes 原始的字符串对应的字节数组 * @return 经历赫夫曼编码处理的字节数组 */ private static byte[] huffmanZip(byte[] bytes) { List<Node> nodes=getNodes(bytes); //创建赫夫曼树 Node root=createHuffManTree(nodes); //生成对应的赫夫曼编码(根据赫夫曼树) Map<Byte,String> huffmanCodes=getCodes(root); //根据赫夫曼编码对原始的数组进行压缩 byte[] huffmanCodeBytes=zip(bytes,huffmanCodes); return huffmanCodeBytes; } //前序遍历 private static void preOrder(Node root) { if (root!=null) { root.preOrder(); }else{ System.out.println("哈夫曼树为空"); } } } class Node implements Comparable<Node>{ Byte data;//存放数据 a=97 int weight;//权值,字符出现次数 Node left; Node right; public Node(Byte data, int weight) { this.data = data; this.weight = weight; } @Override public int compareTo(Node node) { return this.weight-node.weight; } //重新toString @Override public String toString() { return "Node{" + "data=" + data + ", weight=" + weight + '}'; } //前序遍历 public void preOrder(){ System.out.println(this); if(this.left!=null) { this.left.preOrder();; } if(this.right!=null) { this.right.preOrder(); } } }


