p1862
文件夹里都堆了20多道没改完的题了,我却又来开了一个新题。
好在一节课时间做出来了。
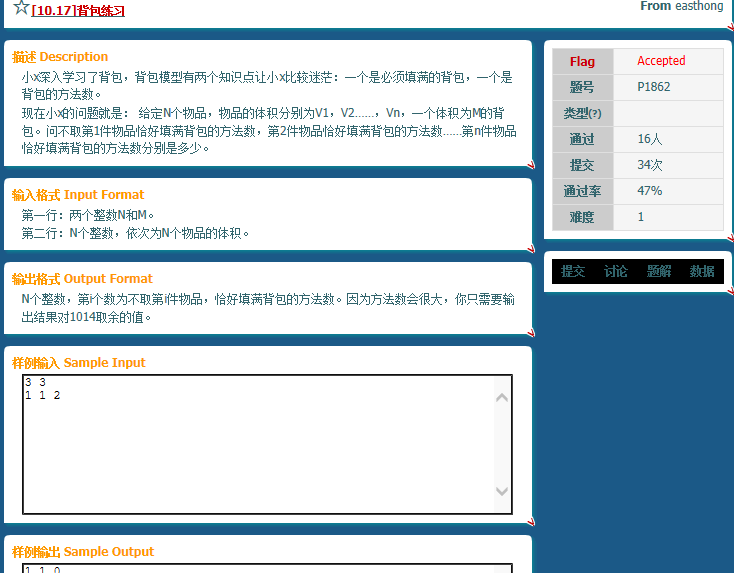

求刚好放满m的方案数。这个到是我没做过的,捣腾了半天弄出来转移方程
ans[0]=1; ans[f]=ans[f-o[i]];
对于n个物品容积为m的背包跑一遍需要m*n的时间,这样子n*m*n就不行了。
不管怎样,先写出来模板好了
ans[0]=1; for(i=1;i<=n;i++) { for(f=m;f>=o[i];f--) { ans[f]+=ans[f-o[i]]; ans[f]%=1014; } }
ans[m]即为所求。
我们来深究一下这个方程。ans[i]表示能恰好装满i体积的物品方案数,那么ans[0]=1,有且只有一种方案。对于每个物品o[i]可以把f体积的方案数转移(加)在f+o[i]上。代码实现时为了不让已经更新过的再去更新别人采取了从后向前的方式。
考虑o[i]的顺序是否影响最终答案呢?当然是不影响的,先加后加都一样的。
考虑在i=n-1的时候ans们表示什么?这时候o[n]还没有去更新答案,相当于没有它,那就相当于前n-1个物品的方案数了。
那么我们把这个f的循环逆着跑一遍,把o[i]加上的再减去,那就相当于没有o[i]的方案数,跑一遍后ans[m]即为所求,输出一下答案。然后再用它更新答案,再把o[i+1]更新的减一遍,再输出答案。一直进行,满足题意。
输出答案的时候是可能有符号的,可以先加上模数保证大于0,然后再取余。
using namespace std; int i,f,k; int n,m,ans[10010]; int o[10010]; int main() { cin>>n>>m; for(i=1;i<=n;i++) cin>>o[i]; ans[0]=1; for(i=1;i<=n;i++) { for(f=m;f>=o[i];f--) { ans[f]+=ans[f-o[i]]; ans[f]%=1014; } }//处理出1-n的 for(k=1,f=o[k];f<=m;f++) { ans[f]-=ans[f-o[k]]; ans[f]%=1014; } cout<<(ans[m]+1014)%1014<<' ';//处理出没有1的并输出 for(;k<=n;) { for(f=m;f>=o[k];f--)//把o[k]再加回去 { ans[f]+=ans[f-o[k]]; ans[f]%=1014; } k++; for(f=o[k];f<=m;f++)//把[k]更新过的减去 { ans[f]-=ans[f-o[k]]; ans[f]%=1014; } cout<<(ans[m]+1014)%1014<<' ';//输出答案 if(k==n) return 0; } }



