我会树状数组啦哈哈哈
树状数组资瓷的基本操作有两个,第一个是查询前缀和,第二个是单点增加。利用差分的思想可以达到区间增加和单点查询的操作,复杂度全是log元素数量,十分优秀。
(说起来用c[i]减c[i-1]也可以在2*logn的时间单点查询.
我甚至还能存一下本来的数组,就是O(1)了)
如果不用增加了的话也可以建立数组sum[i]=sum[i-1]+o[i],查询时间也是1.
这里的c数组就是树状数组的表示方式了。这个玩意儿真的是靠lowbit()一手撑起来的数据结构了……
lowbit(i)表示i二进制分解后第一个出现1的位置,也是c[i]在原数组中表示的元素和的长度。
lowbit()的代码如下。什么?你问我证明?它就是那样的嘛,我的老师又没讲,怪我喽。
int lowbit(int x)//这里的x一定要是非负整数int { return x&(-x); }
怎么利用呢,就是c[i]=∑o[f],(i-lowbit(i)<f<=i);为什么呢?因为建立的时候就是按这个规则建立的,我这样说你懂了吧?
这个时候应该放一个图了……
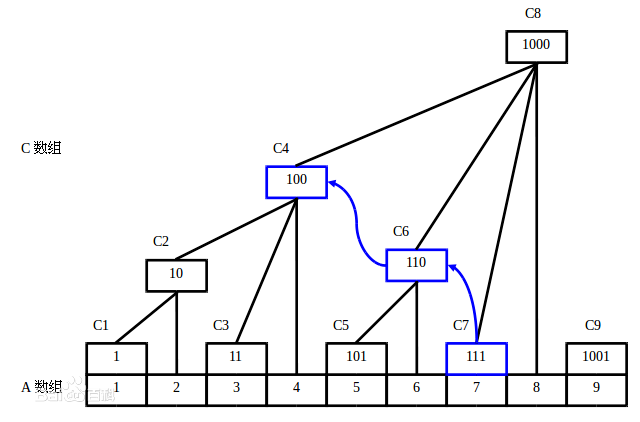
其实只要看这个图自己手推一会就能明白很多了,推荐大家输出一下1-9的lowbit(),一点就通。
假设我们已经建好了,那输出sum[n]就可以把c[n]利用lowbit()向前推,一直推进零里,经过的节点一定完全覆盖了1-n的原数组了
1 for(i=n,ans=0;i!=0;i-=lowbit(i)) 2 ans+=c[i];
证明嘛,自己看图好了。
那么如何建立呢?根据图可以得出c[i]的父节点是c[i+lowbit(i)],那么c[i]加一个值它的父节点们也加一波就完事了。
它的空间复杂度是n,也就是说加到c[n]以后一定停下来,那么就有代码
for(f=i;f<=n;f+=lowbit(f))//n为原数组元素数量 c[f]+=o[i];
修改的话是差不多的。比如把o[x]加t就是这样弄
o[x]+=t; for(;x<=n;x+=lowbit(x)) c[x]+=t;
t当然也能是负数啦。
以上是基础操作。那么如何利用它的特性进行区间增加和单点查询呢?
有一个很奇妙且不好想的方法就是利用差分。
我们令原数组为o[i],处理出差分数组a[i]=o[i]-o[i-1]。此时o[1]=a[1],o[2]=a[1]+a[2],o[3]=a[1]+a[2]+a[3],……以此类推。然后再对于a[i]处理出c[i],就可以利用树状数组在logn的事件查询出∑a[i](1<=i<=n)的值,它就是原来的原来数组o[i]了。
区间增加相当于把该区间内的数同时加t,那么区间内相邻元素的变化量是不变的,而o[左端点]就要比o[左端点-1]在原来基础上多t,o[右端点+1]比o[右端点]在原来基础上少了t。
因此要把a[左端点]+=t,a[右端点+1]-=t。对c的操作就照搬上面了。
来一个例题好了。

想用动态规矩的朋友们就算了,32000*32000搞不了的,前缀和也没啥用。
那么这题咋弄呢?他需要一个n*log?级别的算法,可以想一想树状数组了,支持修改和查询刚好是前缀和。
既然输入的时候已经排好序了,我们每次输入进来一个点就输出xi和xi以前点的个数,这个需要logxi的时间,然后再把xi这一点的个数++(也就是第一种树状数组的单点增加的操作)这样跑一边就是n*log32000的复杂度,十分优秀。
然而x可以等于0,在add的操作中由于lowbit(0)=0.就动不了了,导致超时并且丢50分。我的一个方法是设置一个sum0专门表示x=0的点的个数:输入时总输出sum(x)+sum0,如果这个点x=0就sum0++,否则add(x);

1 #include<iostream> 2 #include<cstdio> 3 #include<cstdlib> 4 #include<cstring> 5 #include<cmath> 6 #include<string> 7 #include<algorithm> 8 #include<vector> 9 #include<map> 10 #include<stack> 11 #include<queue> 12 #include<deque> 13 #include<set> 14 using namespace std; 15 int i,tx,ty; 16 int n; 17 int c[32010],sum0; 18 int lowbit(int x) 19 { 20 return x&(-x); 21 } 22 void add(int p) 23 { 24 25 while(p<=32000) 26 { 27 c[p]++; 28 p+=lowbit(p); 29 } 30 } 31 int sum(int x) 32 { 33 int ans=0; 34 while(x) 35 { 36 ans+=c[x]; 37 x-=lowbit(x); 38 } 39 return ans; 40 } 41 int main() 42 { 43 ios::sync_with_stdio(false); 44 cin.tie(NULL); 45 cout.tie(NULL); 46 //freopen("123.in","r",stdin); 47 cin>>n; 48 for(i=1;i<=n;i++) 49 { 50 cin>>tx>>ty; 51 cout<<sum(tx)+sum0<<endl; 52 if(tx==0)sum0++; 53 else 54 add(tx); 55 56 } 57 }
以上还是基础操作。我们如何用树状数组完成区间修改区间查询的操作呢。这显然是线段树的活,现在考虑如何用树状数组维护。
以下需要乘法分配律的知识。
既然区间求和还是想差分。先对于原数组o[i]求一个差分数组b[i]=a[i]-a[i-1];那么查询区间和还可以使用容斥减一减,看来只需要求[1,x]的区间就行了。
我们推一下这两个式子:这里a是原数组,d是差分数组。
 (转载自https://www.cnblogs.com/lcf-2000/p/5866170.html)
(转载自https://www.cnblogs.com/lcf-2000/p/5866170.html)
用两个树状数组维护d[i]与d[i]*i即可。
哎呀真丢人。
放一个模板算了。

1 int i,t,r,l,v; 2 int n,m; 3 int a[100010],b[100010]; 4 int c1[100010],c2[100010]; 5 inline int lowbit(int x) 6 { 7 return x&(-x); 8 } 9 inline void add1(int x,int v) 10 { 11 for(;x<=n;x+=lowbit(x)) 12 { 13 c1[x]+=v; 14 } 15 return ; 16 } 17 inline void add2(int x,int v) 18 { 19 for(;x<=n;x+=lowbit(x)) 20 { 21 c2[x]+=v; 22 } 23 return ; 24 } 25 inline int sum1(int x) 26 { 27 int ans=0; 28 for(;x;x-=lowbit(x)) 29 { 30 ans+=c1[x]; 31 } 32 return ans; 33 } 34 inline int sum2(int x) 35 { 36 int ans=0; 37 for(;x;x-=lowbit(x)) 38 { 39 ans+=c2[x]; 40 } 41 return ans; 42 } 43 int main() 44 { 45 n=read();m=read();/* 46 for(i=1;i<=n;i++) 47 { 48 a[i]=read();t=a[i]-a[i-1]; 49 add1(i,t); 50 add2(i,(i-1)*t); 51 }*/ 52 for(i=1;i<=m;i++) 53 { 54 t=read(); 55 if(t==1)//修改操作 56 { 57 l=read();r=read();v=read(); 58 add1(l,v); 59 add1(r+1,-v); 60 add2(l,v*(l-1)); 61 add2(r+1,-v*r); 62 } 63 else//求和操作 64 { 65 l=read();r=read(); 66 write( r*sum1(r)-(l-1)*sum1(l-1)-sum2(r)+sum2(l-1)); 67 putchar(10); 68 } 69 } 70 return 0; 71 }
虽然代码也长,但是比线段树看起来好懂许多吧。跑得还快。




