p1951

 

第一眼看到以为也是贪心(毕竟毕竟喜欢贪心的题)。

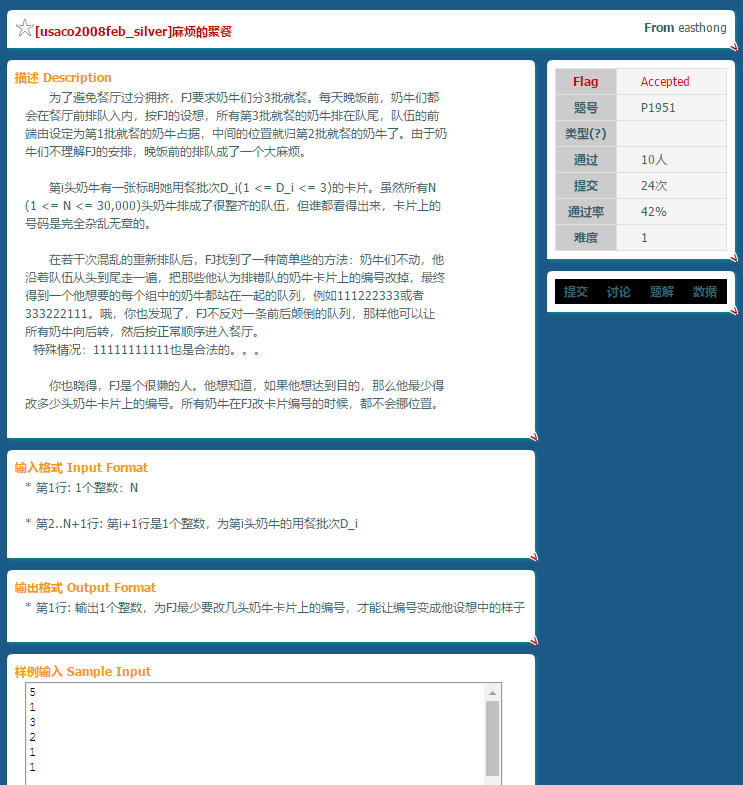
本题中要求把一个数列改成单调的数列，允许全为一个数。求改动的最少的次数。

最基础的想法是先求出每个位置以前包括自己1、2、3的个数sum1[i],sum2[i],sum3[i]。然后再枚举一的截止位点和二的截止位点，次数就可以直接求出。

公式如下(i取0到n，f取i到n)

1 2 3递增序列
ans=min(n-sum1[i]-sum2[f]+sum2[i]-sum3[n]+sum3[f],ans);
3 2 1递减序列
ans=min(n+sum1[f]-sum1[n]+sum2[i]-sum2[f]-sum3[i],ans);

这样下来复杂度是n^2，我不知道咋算的以为不会超时，以为应该是正解了吧，但被打脸了。(但是由于过水的数据还拿了90分)

想正解的过程中先想到的是空间换时间，然后一个动态规划的写法就很快出炉了：

在递增的时候维护ans[1][i] 、ans[2][i]、ans[3][i]分别表示第i个数为1、2、3时改动的个数，那么有这样的转移方程(minn返回三者的最小值)

//自己理解吧
ans[1][i]=ans[1][i-1];
ans[2][i]=min(ans[1][i-1],ans[2][i-1]);
ans[3][i]=minn(ans[1][i-1],ans[2][i-1],ans[3][i-1]);

if(o[i]==1)
{
    ans[2][i]++;
    ans[3][i]++;
}
if(o[i]==2)
{
    ans[1][i]++;
    ans[3][i]++;
}
if(o[i]==3)
{
    ans[1][i]++;
    ans[2][i]++;
}

相似的，递减的时候可以这样弄

ans[3][i]=ans[3][i-1];
ans[2][i]=min(ans[3][i-1],ans[2][i-1]);
ans[1][i]=minn(ans[3][i-1],ans[2][i-1],ans[1][i-1]);

if(o[i]==3)
{
    ans[2][i]++;
    ans[1][i]++;
}
if(o[i]==2)
{
    ans[3][i]++;
    ans[1][i]++;
}
if(o[i]==1)
{
    ans[3][i]++;
    ans[2][i]++;
}

最后的答案是两次循环后在ans[1/2/3][n]中取最小值。

本题AC