p1450

 

 

题目本来不难，但我不会邻接表哇，所以拖到了现在。

刚开始还以为可以上并查集，但是努力了一下后发现应该不行。

先推一下样例好了。图画出来如下所示：

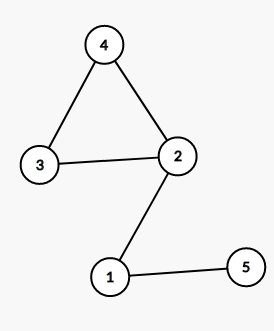
答案里的三就是这个环的长度。

那么本题的目的就可以得出来了：已知n个顶点和n个边，求图中最小的环的大小。

本题中边的数目较小，是一个稀疏图。而顶点的数目对于二维数组就太大了，所以邻接表就少不了。

于是我恶补了一下邻接表，终于明白了邻接表的工作原理：利用结构体，同时存下每条边的起点、终点、上一条边再结构体的下标(如果是第一条边就为0)，复杂度是边的数量。再建立一个数组记下每一个节点最后一个边的下标。

模板就是这样的

struct node
{
  int x,y,next;
}a[200010];
int LINK[200010],len=0;
void insert(int xx,int yy,int vv)
{
    a[++len].next=LINK[xx];
    LINK[xx]=len;
    a[len].x=xx;
    a[len].y=yy;
    a[len].v=vv;
}

如果是无向图就建两次，复杂度为2*边的数量。

回到本题：直接搜索。

我们弄一个标记数组记录是否搜过这个点，如果搜过了就不搜了(说的跟废话一样)。对于每没到过个点进去dfs找它的所有连到的点，如果这个点连到了现在的起点i就更新答案。

再加一个优化：找完一个点i后可以把i的数组弄成1，因为如果这个点在一个环内，再以环上的起点经过它搜索已经没有意义；如果它不在任何一个环内，那经过它就更没有用了。

最后的答案如下：

#include <cstdio>
#include <iostream>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
using namespace std;
inline int read()
{
    int x=0;
    char ch=getchar();
    while(ch>'9'||ch<'0')
        ch=getchar();
    while(ch>='0'&&ch<='9')
    {
        x=(x<<1)+(x<<3)+ch-'0';
        ch=getchar();
    }
    return x;
}
int i,f;
int n,x,ans;
bool flag[200010];
struct node
{
    int x,y,next;
}a[400010];
int LINK[400010],len=0;
void insert(int xx,int yy)
{
    a[++len].next=LINK[xx];
    LINK[xx]=len;
    a[len].x=xx;
    a[len].y=yy;
}
void dfs(int t,int now)
{
    flag[t]=1;
    for(int j=LINK[t];j!=0;j=a[j].next)
    {        
        if(now>1&&a[j].y==i)
        {
            ans=min(ans,now+1);
        }
        if(flag[a[j].y]==0)        
            dfs(a[j].y,now+1);
    }
    flag[t]=0;
    return ;
}
int main()
{
//freopen("123.in","r",stdin);
//freopen("123.out","w",stdout);
    
int __size__ = 20 << 20; // 20MB
char *__p__ = (char*)malloc(__size__) + __size__;
__asm__("movl %0, %%esp\n" :: "r"(__p__));//为了不爆栈。。
    n=read();
    ans=n*2;
    for(i=1;i<=n;i++)
    {
        x=read();
        insert(i,x);
        insert(x,i);
    }
    for(i=1;i<=n;i++)
    {
        dfs(i,0);
        flag[i]=1;
    }
    cout<<ans;
}

 这题磨完了以后就可以进军图论了(吧)， (＾－＾)V