天津大学夏令营机试题目

首先我没参加机试，所以我都是口胡的做法，大概率能对吧

 

 

 

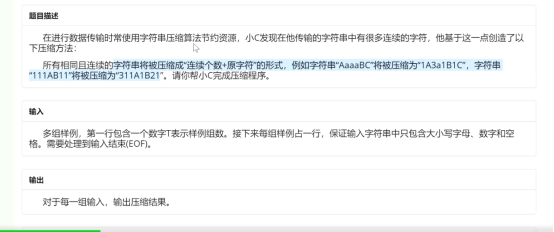
简单模拟，双指针或者什么的搞一搞，使用getline输入

string s;
int n;
void work()
{
    getline(cin,s);
    n=s.length();
    for(int i=0;i<n;i++)
    {
        int j=i;
        while(j+1<n&&s[j+1]==s[i])
            j++;
        printf("%d%c",j-i+1,s[i]);
        i=j;
    }
    printf("\n");
}
int main() 
{
    // freopen("1.in","r",stdin);
    int t=read();
    getline(cin,s);
    for(;t;t--)
        work();
}

2

 

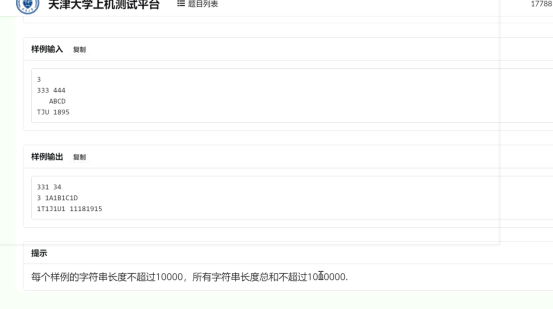
 s和t的范围没给，不妨认为是int范围内

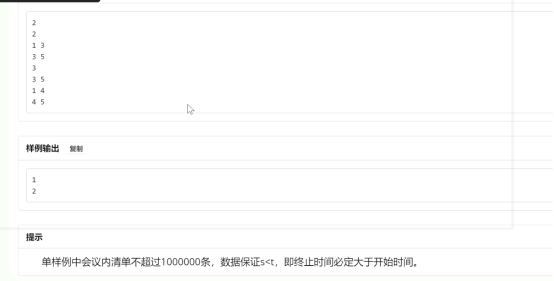
问题是询问数轴上最多有几个区间同时覆盖一个点

那么做法很多，例如离散化后用差分的思想求出每个坐标有几个区间覆盖，取max。我的做法是把左右端点拿出来，sort一下后跑一遍

struct node
{
    int t,f;
    friend bool operator <(node a,node b)
    {
        if(a.t==b.t)
            return a.f>b.f;
        return a.t<b.t;
    }
}o[2000010];
int n,ans,sum;
void work()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        o[i].t=read();
        o[i].f=0;
        o[i+n].t=read();
        o[i+n].f=1;
    }
    sort(o+1,o+1+2*n);
    ans=0;
    for(int i=1;i<=2*n;i++)
    {
        if(o[i].f)
            sum--;
        else
            sum++;
        ans=max(ans,sum);
    }
    printf("%d\n",ans);
}
int main()
{
    // freopen("1.in","r",stdin);
    for(int t=read();t;t--)
        work();

}

3

 

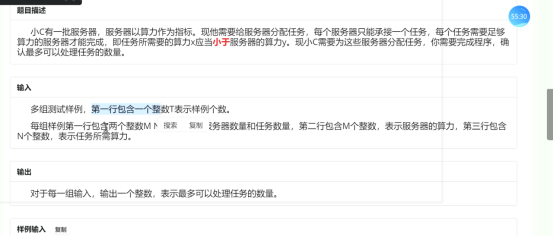
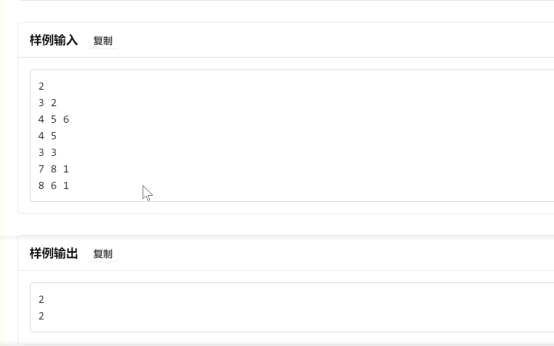
 也没给范围，不妨认为(n+m)log(n)跑得过，时间是int范围内正整数

考虑贪心

用大根堆存一下服务器和任务，然后开始枚举服务器，分配任务。（或者你枚举任务分配服务器也是可以的）

int n,m,ans;
priority_queue<int>a,o;
void work()
{
    m=read();n=read();
    while(o.size())o.pop();
    while(a.size())a.pop();
    ans=0;
    for(int i=1;i<=m;i++)
        o.push(read());//服务器
    for(int i=1;i<=n;i++)
        a.push(read());
    while(o.size())
    {
        while(a.size()&&a.top()>=o.top())
            a.pop();
        if(a.size())
            a.pop(),ans++;
        else
            break;
        o.pop();
    }
    printf("%d\n",ans);
}
int main()
{
    // freopen("1.in","r",stdin);
    for(int t=read();t;t--)
        work();

}

4

 

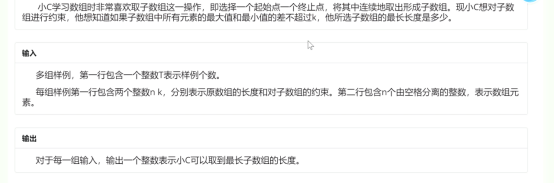
 范围又没给，不妨认为nlogn跑得过，元素和k是int范围内

考虑双指针，左端点每移动一次，右端点尽可能地向右移动。区间里的元素用multiset维护，即可log复杂度地插入删除和询问区间元素的最大值最小值之差

int n,k,a[1000010],ans;
multiset<int>o;
void work()
{
    n=read();k=read();
    for(int i=1;i<=n;i++)
        a[i]=read();
    o.clear();ans=0;
    for(int l=1,r=0;l<=n;l++)
    {
        if(l>r)
            o.insert(a[l]),r=l;
        while(r<n&&max(a[r+1],*o.rbegin())-min(a[r+1],*o.begin())<=k)
        {
            r++;
            o.insert(a[r]);
        }
        ans=max(ans,r-l+1);
        o.erase(o.find(a[l]));
    }
    printf("%d\n",ans);
}
int main()
{
    // freopen("1.in","r",stdin);
    for(int t=read();t;t--)
        work();

}

 

5

 

 

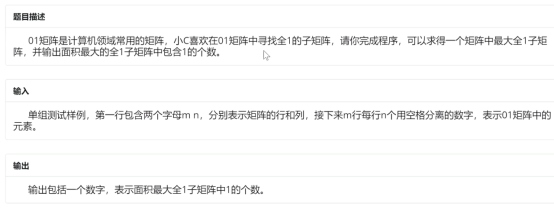
 暴力做法当然是预处理二维前缀和数组，n^4地枚举矩阵，看看矩阵里的1的数量是不是满的

n^4做不了，我们需要n^3的做法

考虑dp，f[x][y][len]表示以xy为右下角，宽为len的矩阵最高能多高

那么如果x,y-len+1到xy都是1，f[x][y][len]=f[x-1][y][len]+1

如果不都为1，那么f[x][y][len]=0

那么对于xy，随着len增大用一个flag记录是否全1，即可n^3地得到f[x][y][len]。对于每个f[x][y][len],ans=max(ans,f[x][y][len]*len)更新答案

空间大概率会挂，注意到第x行的状态只和第x-1行有关，所以使用滚动数组即可做到空间复杂度n^2

int a[510][510],n,m,f[2][510][510],ans;
int main()
{
    // freopen("1.in","r",stdin);
    n=read();m=read();
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            a[i][j]=read();
    for(int x=1;x<=n;x++)
    {
        for(int y=1;y<=m;y++)
        {
            int flag=1;
            for(int len=1;len<=y;len++)
            {
                flag=flag&a[x][y-len+1];
                if(flag)
                    f[x&1][y][len]=f[x&1^1][y][len]+1;
                else
                    f[x&1][y][len]=0;
                ans=max(ans,len*f[x&1][y][len]);
            }
        }
    }
    cout<<ans;

}