2023 CCPC河南省赛题解12/12
https://codeforces.com/gym/104354
A
注意到a串最大长度也就26，所以可以枚举a串，判断剩下的串是不是回文的。
#include<bits/stdc++.h> using namespace std; typedef long long ll; ll read() { ll x;scanf("%lld",&x);return x; } char s[100010]; int f[300],n; int check(int l,int r) { while(l<r) { if(s[l]!=s[r]) return 0; l++; r--; } return 1; } void work() { scanf("%s",s+1); n=strlen(s+1); for(int i='a';i<='z';i++) f[i]=0; for(int i=1;i<n;i++) { if(f[s[i]]) break; f[s[i]]=1; if(check(i+1,n)) { printf("HE\n"); return ; } } printf("NaN\n"); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }
B
考虑如果有ai>aj，i<j，那么i和j必须在同一个块里。否则随便划分。
所以贪心地划分成最小的不可再分的几个区间。从l到i，i是右端点当且仅当区间最大值小于等于后面的最小值。
把这些右端点标记一下，满足答案的k必须满足k、2k、3k、4k...都被标记。
预处理后缀最小值，再暴力判断一下合法的k，复杂度nlogn。
int n,a[1000010],m[1000010],f[1000010],ans; int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) a[i]=read(); m[n+1]=a[n]; for(int i=n;i>=1;i--) m[i]=min(m[i+1],a[i]); int maxx=0; for(int i=1;i<=n;i++) { maxx=max(maxx,a[i]); if(maxx<=m[i+1]||i==n) { f[i]=1; maxx=0; } } for(int k=1;k<=n;k++) { ans++; for(int i=k;i<=n;i+=k) if(f[i]==0) { ans--; break; } } printf("%d",ans); }
C
先跑一个kmp。
因为前100个和中间某一段相同的概率很小，所以kmp一但发现f[i]大于等于100就认为不是随机数即可。
int n,f[1000010]; char s[1000010]; int main() { // freopen("1.in","r",stdin); scanf("%s",s); n=strlen(s); for(int i=1;i<n;i++) { int j=f[i-1]; while(j>0&&s[i]!=s[j]) j=f[j-1]; if(s[i]==s[j]) j++; f[i]=j; if(f[i]>=100) { printf("No"); return 0; } } printf("Yes"); }
D
首先来点特例：
n=1或者颜色大于边数的话输出1 1。把没有连边的点删了，删了不会影响答案。删了若干个点之后发现某个点没有连边了，那么也需要删掉。可以用dfs来做这个过程。如果剩下没点了也可以输出11。
那么带着非孤立点和有用的边继续出发。
考虑做n轮删边操作：先用当前的边跑并查集。然后对于每条边，如果相连的点的归属情况不同，就可以把这个边删了。
删了这么多边后，就只剩下有用的边，并且所有的点所属并查集情况相同。找一找最大的并查集大小并输出即可。
#include<bits/stdc++.h> using namespace std; typedef long long ll; ll read() { ll x; scanf("%lld",&x); return x; } #define M 2000010 #define N 501 struct edge { int x,y,v; friend bool operator <(edge x,edge y) { return x.v<y.v; } } e[M]; int n,m,in[N],sum[N],minf[N],maxf[N]; vector<short>f[N]; int k; vector<pair<int,int>>ee[N]; int checkin(int x) { for(int i=1; i<=k; i++) if(f[x][i]==0) return 0; return 1; } void dfs(int x) { in[x]=0; for(auto y:ee[x]) { if(in[y.first]==0)continue; f[y.first][y.second]--; if(f[y.first][y.second]==0) sum[y.first]--; if(sum[y.first]==0) dfs(y.first); } } int getfa(int x,int v) { return f[x][v]==x?x:f[x][v]=getfa(f[x][v],v); } void merge(int v,int x,int y) { x=getfa(x,v); y=getfa(y,v); if(x==y)return ; if(x>y)swap(x,y); if(v==1) sum[y]+=sum[x]; f[x][v]=y; } vector<int>num,t[N]; vector<int>resn; void sortn() { num.clear(); for(auto i:resn) num.push_back(i); for(int i=1; i<=k; i++) { for(auto x:resn) t[x].clear(); for(auto x:num) { t[getfa(x,i)].push_back(x); } num.clear(); for(auto i:resn) for(auto x:t[i]) num.push_back(x); } } int check() { for(auto i:resn) { minf[i]=maxf[i]=getfa(i,1); for(int j=1; j<=k; j++) { minf[i]=min(minf[i],(int)f[i][j]); maxf[i]=max(maxf[i],(int)f[i][j]); } } for(auto i:resn) for(int j=1; j<=k; j++) if(f[i][j]!=f[i][1]) return 0; return 1; } void work() { k=read(); n=read(); m=read(); resn.clear(); for(int i=1; i<=n; i++) ee[i].clear(); for(int i=1; i<=m; i++) { e[i].v=read(); e[i].x=read(); e[i].y=read(); ee[e[i].x].push_back({e[i].y,e[i].v}); ee[e[i].y].push_back({e[i].x,e[i].v}); } if(n==1||k>m) { printf("1\n1\n"); return ; } for(int i=1; i<=n; i++) f[i].resize(m+1); for(int i=1; i<=n; i++) { in[i]=1; for(int j=1; j<=m; j++) f[i][j]=0; } for(int i=1; i<=m; i++) { if(f[e[i].x][e[i].v]==0) sum[e[i].x]++; if(f[e[i].y][e[i].v]==0) sum[e[i].y]++; f[e[i].x][e[i].v]++; f[e[i].y][e[i].v]++; } for(int i=1; i<=n; i++) { if(in[i]&&checkin(i)==0) { dfs(i); } if(in[i]) resn.push_back(i); } if(resn.size()==0) { printf("1\n1\n"); return ; } int t=0; for(int i=1; i<=m; i++) { if(in[e[i].x]==0||in[e[i].y]==0) continue; t++; e[t]=e[i]; } m=t; for(int jj=1;jj<=resn.size();jj++) { for(auto i:resn) { for(int j=1; j<=k; j++) { f[i][j]=i; } sum[i]=1; } for(int i=1; i<=m; i++) { merge(e[i].v,e[i].x,e[i].y); } sortn(); if(check()) { break; } int t=0; for(int i=1; i<=m; i++) { if(minf[e[i].x]==minf[e[i].y]&&maxf[e[i].x]==maxf[e[i].y]) { t++; e[t]=e[i]; } } m=t; } int ans=resn[0]; for(auto i:resn) if(sum[getfa(i,1)]>sum[f[ans][1]]) ans=i; printf("%d\n",sum[f[ans][1]]); for(auto i:resn) if(f[ans][1]==getfa(i,1)) printf("%d ",i); printf("\n"); } int main() { // freopen("1.in","r",stdin); // freopen("1.out","w",stdout); for(int t=read(); t; t--) work(); }
E
dp一下
基本转移方式是从f[i-1][j][k]和f[i][j-1][k]转移过来，如果是1可以+1，否则不能加
高级的转移是如果当前是问号，可以从f[i-1][j][k-1]和f[i][j-1][k-1]转移过来并加一。如果k=0就不能有这个转移。
空间开不下，所以压缩一下。
int n,m,x,f[2][510][1010]; char s[510][510]; void work() { n=read();m=read();x=read(); for(int i=1;i<=n;i++) scanf("%s",s[i]+1); for(int i=0;i<=m;i++) for(int j=0;j<=x;j++) f[0][i][j]=f[1][i][j]=0; for(int i=1;i<=n;i++) { for(int j=1;j<=m;j++) { if(s[i][j]=='1') f[i&1][j][0]=max(f[i&1][j-1][0],f[(i-1)&1][j][0])+1; else f[i&1][j][0]=max(f[i&1][j-1][0],f[(i-1)&1][j][0]); for(int k=1;k<=x;k++) { if(s[i][j]=='1') f[i&1][j][k]=max(f[i&1][j-1][k],f[(i-1)&1][j][k])+1; else f[i&1][j][k]=max(f[i&1][j-1][k],f[(i-1)&1][j][k]); if(s[i][j]=='?') f[i&1][j][k]=max(f[i&1][j][k], max(f[i&1][j-1][k-1],f[(i-1)&1][j][k-1])+1); } } } int ans=f[n&1][m][0]; for(int i=1;i<=x;i++) ans=max(ans,f[n&1][m][i]); printf("%d\n",ans); } int main() { // freopen("1.in","r",stdin); // freopen("1.out","w",stdout); for(int t=read();t;t--) work(); }
F
sort一下，然后枚举所有长为k的子串。
min(|a[i]-a[j]|)是所有相邻数字的差的最小值，用multiset维护一下。max(|a[i]-a[j]|)显然是子串的左右两端。
ll n,k,a[500010],ans; multiset<ll>o; int main() { n=read();k=read(); for(int i=1;i<=n;i++) a[i]=read(); sort(a+1,a+1+n); for(int i=1;i<k;i++) o.insert(a[i+1]-a[i]); ans=*o.begin()*(a[k]-a[1]); for(int i=k;i<=n;i++) { ans=min(ans,*o.begin()*(a[i]-a[i-k+1])); o.erase(o.find(a[i-k+2]-a[i-k+1])); o.insert(a[i+1]-a[i]); } printf("%lld",ans); }
G
大胆模拟
判断INF我刚开始用了log10，wa了，就换了用1e18除x的方式，稳定不出错。
害怕substr慢就用模拟的方式写了写。本来ans[i]+=substr就很好写的。
以及赛时我只能用pta。如果给我dev的话处理数据本来很快的。
郑轻罪大恶极
char a[][100]={"", ".................................................................................", ".................................................................................", ".0000000.......1.2222222.3333333.4.....4.5555555.6666666.7777777.8888888.9999999.", ".0.....0.......1.......2.......3.4.....4.5.......6.............7.8.....8.9.....9.", ".0.....0.......1.......2.......3.4.....4.5.......6.............7.8.....8.9.....9.", ".0.....0.......1.2222222.3333333.4444444.5555555.6666666.......7.8888888.9999999.", ".0.....0.......1.2.............3.......4.......5.6.....6.......7.8.....8.......9.", ".0.....0.......1.2.............3.......4.......5.6.....6.......7.8.....8.......9.", ".0000000.......1.2222222.3333333.......4.5555555.6666666.......7.8888888.9999999.", ".................................................................................", }; char b[100][100]={"", ".............................................................", ".00000.....1.22222.33333.4...4.55555.66666.77777.88888.99999.", ".0...0.....1.....2.....3.4...4.5.....6.........7.8...8.9...9.", ".0...0.....1.22222.33333.44444.55555.66666.....7.88888.99999.", ".0...0.....1.2.........3.....4.....5.6...6.....7.8...8.....9.", ".00000.....1.22222.33333.....4.55555.66666.....7.88888.99999.", ".............................................................", ".............................................................", ".............................................................", ".............................................................", }; char c[100][100]={"", ".................................", ".................................", ".........IIIIIII.N.....N.FFFFFFF.", "............I....NN....N.F.......", ".=======....I....N.N...N.F.......", "............I....N..N..N.FFFFFFF.", ".=======....I....N...N.N.F.......", "............I....N....NN.F.......", ".........IIIIIII.N.....N.F.......", ".................................", }; char ans[20][1000]; int tot; void add(ll x,int d) { stack<int>q; while(x) { q.push(x%10); x=x/10; } while(q.size()) { for(int i=1;i<=10;i++) { if(d==1) for(int j=tot,k=q.top()*8;j<tot+8;j++,k++) ans[i][j]=a[i][k]; else for(int j=tot,k=q.top()*6;j<tot+6;j++,k++) ans[i][j]=b[i][k]; } if(d==1) tot+=8; else tot+=6; q.pop(); } } void INV(int l,int r) { for(int i=1;i<=10;i++) for(int j=tot,tl=l;tl<=r;j++,tl++) ans[i][j]=c[i][tl]; tot=tot+r-l+1; } int check(ll x,ll y) { if(x==1) return 0; ll a=1e18; for(int i=1;i<=y;i++) { if(a<x) return 1; a=a/x; } return 0; } ll quick(ll x,ll y) { if(x==1) return 1; ll t=1; for(;y;y--) t=t*x; return t; } void work() { ll x,y; scanf("%lld^{%lld}",&x,&y); tot=0; add(x,1); add(y,2); INV(0,7); if(check(x,y)) INV(8,31); else add(quick(x,y),1); for(int i=1;i<=10;i++) { ans[i][tot]=0; printf("%s.\n",ans[i]); } printf("\n"); } int main() { // freopen("1.out","w",stdout); for(int t=read();t;t--) work(); }
H
把玩一下推式子即可。再和记得给下界0取max，给上界n*2取min。
int n,k; void work() { n=read();k=read(); printf("%d %d\n",max(0,n-(k-1)/2),min(n*2,n+k/2)); } int main() { // freopen("1.in","r",stdin); // freopen("1.out","w",stdout); for(int t=read();t;t--) work(); }
I
来自官方题解
考虑假如没有正方形，那么纯色2*2是4*n*n个
那么加上n个矩形，每个矩形的四条边上的2*2正方形都是非纯色的，所以答案减去2*X2-2*X1+2*Y2-2*Y1
如果矩形之间没有交点，那么到这里输出就行了，例如样例二
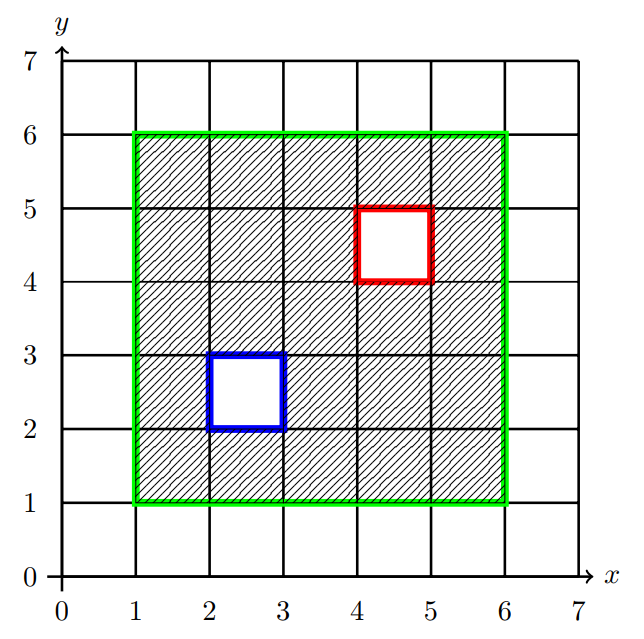
但是如果有交点，那么每个交点会使得一个2*2多减去了一次，我们要加上不同矩形间的交点数量，例如样例一答案是4*3*3-4-8-8+2=18
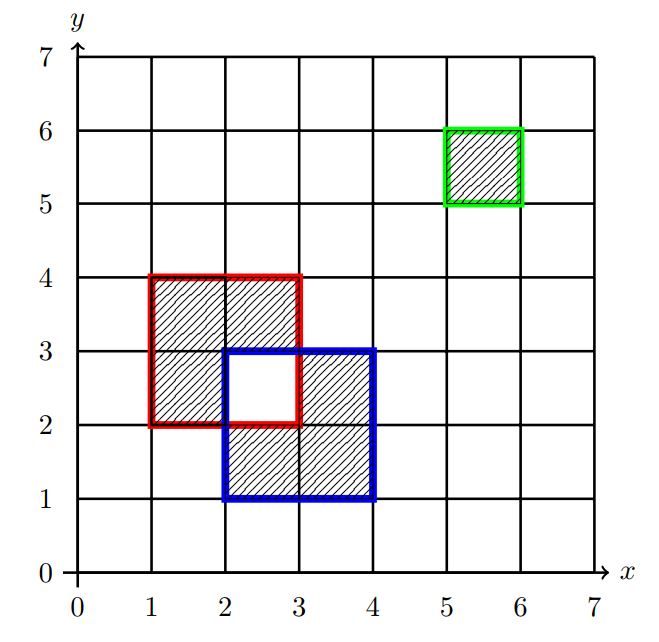
因为本题的特殊性，求交点可以使用树状数组：
对于每条竖线，记录下面的两个端点放在jia数组里，上面的两个端点放在jian数组里。每条横线放在lr里
因为每行一条线段，所以lr数组是满的。同时每行jia数组或者jian数组有且只有一个
考虑枚举每一行，先减，再询问，再加。用树状数组实现单点修改区间询问。
int c[200010],n,jia[200010][2],jian[200010][2],l[200010],r[200010]; ll ans; int lowbit(int x) { return x&(-x); } int ask(int d) { int sum=0; while(d) { sum=sum+c[d]; d=d-lowbit(d); } return sum; } void add(int d,int v) { while(d<=n) { c[d]+=v; d=d+lowbit(d); } } int main() { // freopen("1.in","r",stdin); n=read(); ans=4ll*n*n; int X1,X2,Y1,Y2; for(int i=1;i<=n;i++) { X1=read();Y1=read(); X2=read();Y2=read(); jia[Y1][0]=X1; jia[Y1][1]=X2; jian[Y2][0]=X1; jian[Y2][1]=X2; l[Y1]=X1; r[Y1]=X2; l[Y2]=X1; r[Y2]=X2; ans-=X2*2-X1*2+Y2*2-Y1*2; } n=n*2; for(int i=1;i<=n;i++) { if(jian[i][0]) { add(jian[i][0],-1); add(jian[i][1],-1); } ans+=(ask(r[i])-ask(l[i]-1)); if(jia[i][0]) { add(jia[i][0],1); add(jia[i][1],1); } } cout<<ans; }
J
初中数学。初中数学好并且acos用的熟练即可。不知道为什么赛时没人写（以及我上机最后半小时很急没调出来）
首先点P到线段AB的距离可以用勾股定理求出。斜边为AP，一个直角边为AB/2设为AD，那么P到线段AB的距离即为d=sqrt(ap*ap-ad*ad);
然后开始分类讨论：
如果AB两点在圆内也就是AP<=r，则输出圆的面积
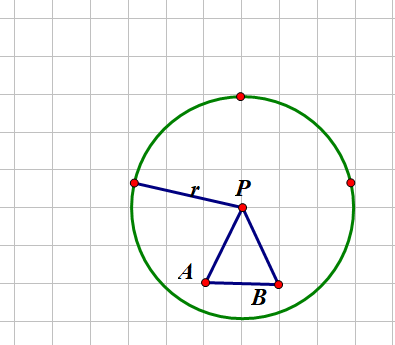
情况二：
若P到AB距离小于等于r，则如上图所示。四个三角形的面积可以勾股定理：斜边为AP，一个直角边为r，则面积为r*sqrt(ap*ap-r*r)/2，四个三角形面积为r*sqrt(ap*ap-r*r)*2
剩下的两个扇形考虑使用弧度制，圆心角为2acos(-1)，∠APC所对圆心角为acos(r/AP)，故剩下的两个扇形所对圆心角为2*acos(-1)-4*acos(r/AP)，面积为(2*acos(-1)-4*acos(r/AP))*r*r/2=(acos(-1)-acos(r/ap)*2)*r*r
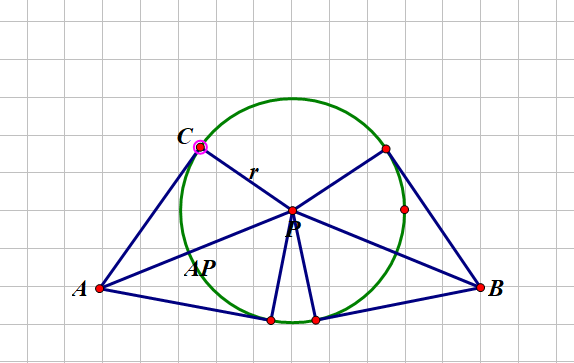
情况三：
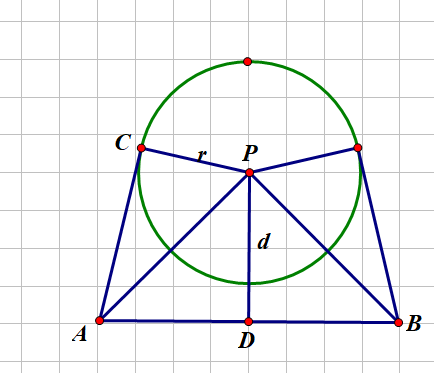
两个小三角形面积可以用勾股定理：斜边为AP，一个直角边为r，则面积为r*sqrt(ap*ap-r*r)/2，两个三角形面积为r*sqrt(ap*ap-r*r)
△ABP的面积为ad*d
圆心角∠ACP的度数为acos(r/ap),圆心角∠APD的度数为acos(d/ap)
所以剩下的扇形所对圆心角为2*acos(-1)-2*acos(r/ap)-2*acos(d/ap)
剩下的扇形的面积为(2*acos(-1)-2*acos(r/ap)-2*acos(d/ap))*r*r/2=(acos(-1)-acos(d/ap)-acos(r/ap))*r*r
总面积为ad*d+r*sqrt(ap*ap-r*r)+(acos(-1)-acos(d/ap)-acos(r/ap))*r*r
struct node { ll x,y; void in() { x=read(); y=read(); } }p,a,b; ll r; double ap,ad,d; double askd(node x,node y) { return sqrt( (x.x-y.x)*(x.x-y.x)+ (x.y-y.y)*(x.y-y.y)); } ll askdd(node x,node y) { return (x.x-y.x)*(x.x-y.x)+ (x.y-y.y)*(x.y-y.y); } void work() { p.in(); a.in(); b.in(); r=read()*read(); ap=askd(a,p); ad=askd(a,b)/2; d=sqrt(ap*ap-ad*ad); if(askdd(a,p)<=r*r) { printf("%.12lf\n",acos(-1)*r*r); } else if(d<=r) { printf("%.12lf\n",r*sqrt(ap*ap-r*r)*2+ (acos(-1)-acos(r/ap)*2)*r*r); } else { double t=sqrt(ap*ap-r*r); printf("%.12lf\n",d*ad+r*t+(acos(-1)-acos(d/ap)-acos(r/ap))*r*r); } } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }
K
唉赛时卡了半天。现在想想主要是hs证明了不能只用2和3，然后就误入歧途了。 void work(int n){ if(n<=4) printf("-1\n"); else if(n==5) printf("4 1 3 5 2\n"); else if(n==6) printf("1 3 5 2 4 6\n"); else if(n==7) printf("1 3 5 2 7 4 6\n"); else if(n==8) printf("1 6 3 8 5 2 7 4\n"); else if(n==11) printf("1 3 10 5 2 7 9 11 8 6 4\n"); else { for(int i=1;i+2<=n;i+=2) { printf("%d ",i); if(i==5) printf("2 "); // if(i==n-6&&i+2!=5) if(i==n-6) printf("%d ",n-1); } printf("%d ",n); for(int i=n-(n&1)-2;i>=4;i-=2) { printf("%d ",i); if(i==n-4) printf("%d ",n-1); } printf("\n"); } } int main() { // freopen("1.in","r",stdin); // freopen("1.out","w",stdout); // for(int t=read();t;t--) work(read()); } F
L
从jiangly代码里抄了一个getPrime才过
int test[]={2,3,5,7,11,13,17,23,29,31,37}; unordered_map<int,bool>mp; ll qpow(ll x,ll y,ll P){ ll ret=1; for (;y;y>>=1,x=x*x%P) if (y&1) ret=ret*x%P; return ret; } bool check(int a,ll P){ ll r=P-1,g=qpow(a,r,P); if (g!=1) return 1; while (r%2==0){ r/=2; g=qpow(a,r,P); if (g==P-1) return 0; else if (g!=1) return 1; } return 0; } bool miller_rabin(int P){ for (int a:test){ if (check(a,P)) return 0; } return 1; } int rnd(){ int t=rand(); t^=rand()<<8; t^=rand()<<16; t^=rand()<<24; return t<0?-t:t; } int getPrime(){ ll t1=rnd()%500000000+5e8; ll t2=1e9-t1; int x=rnd()%t2+t1; while (!miller_rabin(x)||mp.find(x)!=mp.end()) x=rand()%t2+t1; mp[x]=1; return x; } void work() { ll P=getPrime(); cout<<"? 1 "<<P<<endl; ll r=read(); if(!r) { cout<<"! "<<1<<' '<<P<<endl; } else if(r<2*P)//case1 { ll a=r-P+1,b=P; ll t=__gcd(a,b); a=a/t;b=b/t; cout<<"! "<<a<<' '<<b<<endl; } else if(r%P+P<=1000000000&&r%P+P*(r%P+P)==r)//case2.2 { cout<<"! "<<1<<' '<<r%P+P<<endl; } else//case2.1 { ll q1=P-r%P; ll q2=2*P-r%P; ll ansp=(r+q1-q1*P)/P,ansq=q1; if(1<=ansp&&ansp<=ansq&&ansq<=1000000000) cout<<"! "<<ansp<<' '<<ansq<<endl; else cout<<"! "<<(r+q2-q2*P)/P<<' '<<q2<<endl; } read(); } int main() { srand((ll)time(0)); for(int t=read();t;t--) work(); }
