100道codeforces 2400 已完结

浅显的做法是二分+主席树,主席树维护区间里pre都落到了哪。复杂度nlogn^3 int tot,lc[2000000],rc[2000000],c[2000000],pre[100010],rt[100010],n; int build(int x,int l,int r,int d) { tot++; int t=tot; lc[t]=lc[x]; rc[t]=rc[x]; c[t]=c[x]+1; if(l==r) return t; int mid=(l+r)/2; if(d<=mid) lc[t]=build(lc[x],l,mid,d); else rc[t]=build(rc[x],mid+1,r,d); return t; } int ask(int x1,int x2,int l,int r,int tl,int tr) { if(x1==0&&x2==0||tl<=l&&r<=tr) return c[x2]-c[x1]; int mid=(l+r)/2; if(tr<=mid) return ask(lc[x1],lc[x2],l,mid,tl,tr); else if(tl>mid) return ask(rc[x1],rc[x2],mid+1,r,tl,tr); else return ask(lc[x1],lc[x2],l,mid,tl,tr)+ask(rc[x1],rc[x2],mid+1,r,tl,tr); } int ask(int x,int k) { int l=x,r=n,mid; while(l+1<r) { mid=(l+r)/2; if(ask(rt[x-1],rt[mid],0,n,0,x-1)>k)//区间x到mid有多少个pre落在0到x-1 r=mid; else l=mid; } if(ask(rt[x-1],rt[r],0,n,0,x-1)<=k) return r; return l; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { int x=read(); rt[i]=build(rt[i-1],0,n,pre[x]); pre[x]=i; } for(int k=1;k<=n;k++) { int ans=0; for(int i=1;i<=n;i=ask(i,k)+1) ans++; printf("%d ",ans); } } 因为调和级数+二分+主席树,总复杂度有三个log。我们考虑用主席树上二分省掉一个log 把主席树维护的东西反过来,维护pre为i的都从哪来的,就可以主席树上二分了。 因为我只会求第一次等于k的pos,所以求第一次等于k+1的pos再减一就得到了最后一个等于k的pos。 int tot,lc[2000000],rc[2000000],c[2000000],pre[100010],rt[100010],n; queue<int>pos[100010]; int build(int x,int l,int r,int d) { tot++; int t=tot; lc[t]=lc[x]; rc[t]=rc[x]; c[t]=c[x]+1; if(l==r) return t; int mid=(l+r)/2; if(d<=mid) lc[t]=build(lc[x],l,mid,d); else rc[t]=build(rc[x],mid+1,r,d); return t; } int ask(int x1,int x2,int l,int r,int tl,int tr) { if(x1==0&&x2==0||tl<=l&&r<=tr) return c[x2]-c[x1]; int mid=(l+r)/2; if(tr<=mid) return ask(lc[x1],lc[x2],l,mid,tl,tr); else if(tl>mid) return ask(rc[x1],rc[x2],mid+1,r,tl,tr); else return ask(lc[x1],lc[x2],l,mid,tl,tr)+ask(rc[x1],rc[x2],mid+1,r,tl,tr); } void build0(int x,int l,int r) { if(l==r) { if(pos[0].size()&&l==pos[0].front()) c[x]=1,pos[0].pop(); return ; } int mid=(l+r)/2; tot++; lc[x]=tot; tot++; rc[x]=tot; build0(lc[x],l,mid); build0(rc[x],mid+1,r); c[x]=c[lc[x]]+c[rc[x]]; } int askpos(int x,int l,int r,int k) { if(l==r) return l; int mid=(l+r)/2; if(c[lc[x]]>=k) return askpos(lc[x],l,mid,k); else return askpos(rc[x],mid+1,r,k-c[lc[x]]); } int askc(int x,int l,int r,int d) { if(r<=d) return c[x]; int mid=(l+r)/2; if(d<=mid) return askc(lc[x],l,mid,d); else return c[lc[x]]+askc(rc[x],mid+1,r,d); } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { int x=read(); pos[pre[x]].push(i); pre[x]=i; } tot++; build0(1,1,n+1); rt[0]=1; for(int i=1;i<=n;i++) { if(pos[i].size()==0) { rt[i]=rt[i-1]; continue; } rt[i]=build(rt[i-1],1,n+1,pos[i].front()); pos[i].pop(); while(pos[i].size()) rt[i]=build(rt[i],1,n+1,pos[i].front()),pos[i].pop(); } for(int k=1;k<=n;k++) { int ans=0; for(int i=1;i<=n;) { ans++; i=askpos(rt[i-1],1,n+1,k+askc(rt[i-1],1,n+1,i)); } printf("%d ",ans); } }
https://codeforces.com/problemset?order=BY_RATING_ASC&tags=2400-

考虑对于每次修改,先存起来。当修改的点超过100后再跑多源bfs更新dis数组,释放掉这些点。 对于每次询问,答案要么是当前存起来的点,可以枚举+lca。要么是被释放掉的点,可以用dis[x]得到。 复杂度m/siz*n(bfs更新dis)+m*siz*log(n) (lca) int n,m,deep[100010],dis[100010],fa[100010][18]; vector<int>now,e[100010]; queue<int>q; void dfs(int x) { for(auto y:e[x]) { if(y==fa[x][0])continue; fa[y][0]=x; deep[y]=deep[x]+1; dfs(y); } } int lca(int x,int y) { int val=deep[x]+deep[y]; if(deep[x]<deep[y])swap(x,y); for(int i=17;i>=0;i--) if(deep[fa[x][i]]>=deep[y]) x=fa[x][i]; if(x==y) return val-2*deep[x]; for(int i=17;i>=0;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; return val-2*deep[fa[x][0]]; } int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<n;i++) { int x=read(),y=read(); e[x].push_back(y); e[y].push_back(x); dis[i]=0x3f3f3f3f; } dis[n]=0x3f3f3f3f; deep[1]=1; dfs(1); for(int i=1;i<=17;i++) for(int x=1;x<=n;x++) fa[x][i]=fa[fa[x][i-1]][i-1]; now.push_back(1); for(;m;m--) { if(read()&1) now.push_back(read()); else { int x=read(); int ans=dis[x]; for(auto y:now) ans=min(ans,lca(x,y)); printf("%d\n",ans); } if(now.size()==100) { for(auto x:now) { if(dis[x]) { dis[x]=0; q.push(x); } } now.clear(); while(q.size()) { int x=q.front();q.pop(); for(auto y:e[x]) { if(dis[y]>dis[x]+1) { dis[y]=dis[x]+1; q.push(y); } } } } } }

众所周知,大小为n的子树里不同出现次数只有根号n个 所以考虑dsu,用sum维护有多少种颜色出现了i次,用o维护颜色i出现了几次。对于每个k,用o.size得到总颜色数,再枚举sum里的元素,减去不合法的即可。复杂度nlog^2(dsu合并)+m*sqrt(n)*log(每次询问) map<int,int>o[100010],sum[100010]; int c[100010],n,m,ans[100010]; vector<int>e[100010]; vector<pair<int,int>>ask[100010]; void merge(map<int,int> &sum1,map<int,int>&o1,map<int,int>&sum2,map<int,int>&o2) { if(o2.size()>o1.size()) { swap(sum1,sum2); swap(o1,o2); } for(auto x:o2) { if(o1[x.first])//有的话 { sum1[o1[x.first]]--; if(sum1[o1[x.first]]==0) sum1.erase(o1[x.first]); o1[x.first]+=x.second; sum1[o1[x.first]]++; } else { o1[x.first]=x.second; sum1[o1[x.first]]++; } } } void dfs(int x,int fa) { sum[x][1]=1;//有一种颜色=1 o[x][c[x]]=1;//c[x]在x的子树里出现了x次 for(auto y:e[x]) { if(y==fa)continue; dfs(y,x); merge(sum[x],o[x],sum[y],o[y]); } for(auto it:ask[x]) { ans[it.second]=o[x].size(); for(auto y:sum[x]) { if(y.first<it.first) ans[it.second]-=y.second; else break; } } } int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) c[i]=read(); for(int i=1;i<n;i++) { int x=read(),y=read(); e[x].push_back(y); e[y].push_back(x); } for(int i=1;i<=m;i++) { int x=read(); ask[x].push_back({read(),i}); } dfs(1,0); for(int i=1;i<=m;i++) printf("%d\n",ans[i]); }

不会做 看了看别人写的,发现这样写的话是对的。。。 int n; ll ans; priority_queue<int,vector<int>,greater<>>q; int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { int x=read(); q.push(x); if(x>q.top()) { ans=ans+x-q.top(); q.pop(); q.push(x); } } cout<<ans; }
第一步,考虑得到f[x]表示有多少个a[i]&x=x
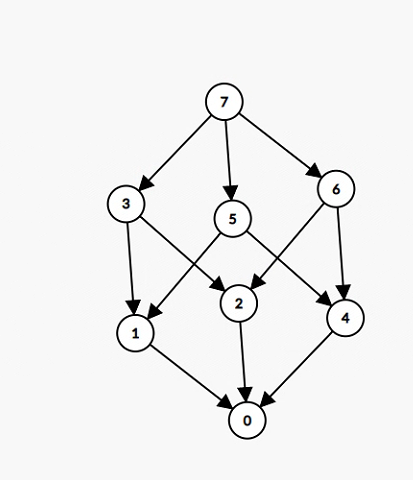
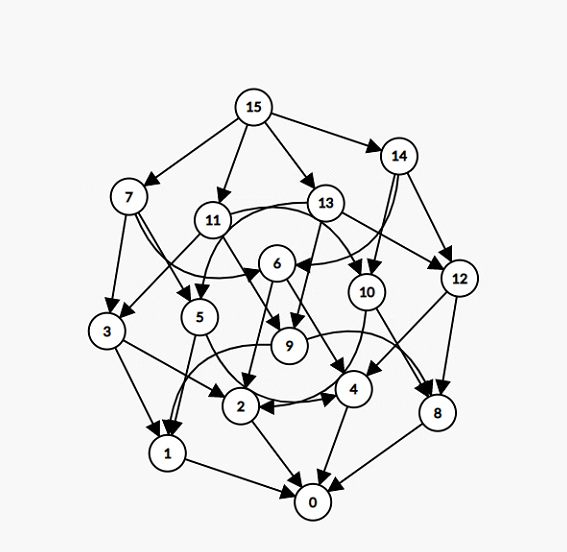
f[x]可以看做是ai刚开始位于自己的位置,开始跑动态规划。最终的f[x]是有多少点“汇入”了x号点。
注意到15到3有两种路径:15->7->3和15->11->3。为了避免重复,规定dp时从小到大枚举1<<j,那么路径就只会是先减去小的1<<j,再减去大的1<<j也就是先有f[11]+=f[15],再有f[3]+=f[11]
第二步就好说了,大胆容斥一下。
(update:原来这个叫高维前缀和)

#include<bits/stdc++.h> using namespace std; typedef long long ll; int read() { int x;scanf("%d",&x);return x; } ll mod=1000000007; int n,POW[3000010],f[3000010],ans; int main() { // freopen("1.in","r",stdin); n=read(); POW[0]=1; for(int i=1;i<=n;i++) { f[read()]++; POW[i]=POW[i-1]*2%mod; } for(int j=0;j<=20;j++) for(int i=0;i<(1<<20);i++) if((i&(1<<j))==0) f[i]=(f[i]+f[i+(1<<j)])%mod; for(int i=0;i<(1<<20);i++) { int now=1; for(int j=0;j<=20;j++) if(i&(1<<j)) now=now*-1; ans=ans+now*POW[f[i]]; ans=(ans%mod+mod)%mod; } cout<<ans; }

斜率优化dp f[i]=max(f[j]+(x[i]-x[j])*y[i])-a[i]) f[i]+a[i]-x[i]*y[i]=max(f[j]-x[j]*y[i]) 是把每个点看做坐标为(x[j],f[j])的点,f[j]-x[j]*y[i]是在求最大的截距,因此用vector维护上凸包即可。询问答案时在凸包里二分查找斜率yi来找切点。 struct node { ll x,y,a; friend bool operator <(node a,node b) { return a.x<b.x; } }o[1000010]; ll n,ans,f[1000010]; struct ttt { ll x,f; }; vector<ttt>q; int ask(ttt a,ttt b,ttt c) { return 1.0*(c.f-b.f)/(c.x-b.x)>=1.0*(b.f-a.f)/(b.x-a.x); } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { o[i].x=read(); o[i].y=read(); o[i].a=read(); } sort(o+1,o+1+n); int now=0; q.push_back({0,0}); for(int i=1;i<=n;i++) { while(now+1<q.size()&&q[now].f-o[i].y*q[now].x<q[now+1].f-o[i].y*q[now+1].x) now++; f[i]=q[now].f-o[i].y*q[now].x-o[i].a+o[i].x*o[i].y; while(q.size()>=2&&ask(q[q.size()-2],q[q.size()-1],{o[i].x,f[i]})) q.pop_back(); q.push_back({o[i].x,f[i]}); now=min(now,(int)q.size()-1); ans=max(ans,f[i]); } cout<<ans; }

考虑离线地处理询问 用线段树维护只有1-o[i].r这些数字时,对于每个位置,如果是最后一次出现,线段树的值为上一次出现的下标,否则为inf 那么对于区间o[i].l,o[i].r,如果区间最小值大于等于o[i].l,证明区间里没有只出现一次的数字。否则找到最小值在哪里,他的值为合法的答案。 int n,a[500010],ans[500010],pos[500010]; pair<int,int>minn[4000010]; struct node { int l,r,i; }o[500010]; bool r_(node a,node b) { return a.r<b.r; } void add(int x,int l,int r,int d,int v) { if(l==r) { minn[x]={v,d}; return ; } int mid=(l+r)/2; if(d<=mid) add(x*2,l,mid,d,v); else add(x*2+1,mid+1,r,d,v); minn[x]=min(minn[x*2],minn[x*2+1]); } pair<int,int> ask(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return minn[x]; int mid=(l+r)/2; if(tr<=mid) return ask(x*2,l,mid,tl,tr); else if(tl>mid) return ask(x*2+1,mid+1,r,tl,tr); else return min(ask(x*2,l,mid,tl,tr),ask(x*2+1,mid+1,r,tl,tr)); } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) a[i]=read(); int q=read(); for(int i=1;i<=q;i++) { o[i].l=read(); o[i].r=read(); o[i].i=i; } sort(o+1,o+1+q,r_); for(int i=1;i<=q;i++) { for(int j=o[i-1].r+1;j<=o[i].r;j++) { if(pos[a[j]]) add(1,1,n,pos[a[j]],n+1); add(1,1,n,j,pos[a[j]]); pos[a[j]]=j; } pair<int,int>t=ask(1,1,n,o[i].l,o[i].r); if(t.first<o[i].l)//last,pos 寻找最小last ans[o[i].i]=a[t.second]; } for(int i=1;i<=q;i++) cout<<ans[i]<<'\n'; }

数组开nlogn int n,a[500010],pos[500010],rt[500010],tot; int lc[20000010],rc[20000010]; pair<int,int>minn[20000010]; pair<int,int> ask(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return minn[x]; int mid=(l+r)/2; if(tr<=mid) return ask(lc[x],l,mid,tl,tr); else if(tl>mid) return ask(rc[x],mid+1,r,tl,tr); else return min(ask(lc[x],l,mid,tl,tr),ask(rc[x],mid+1,r,tl,tr)); } int built(int now,int l,int r,int d,int v) { int t=++tot; lc[t]=lc[now];rc[t]=rc[now]; if(l==r) { minn[t]={v,l}; return t; } int mid=(l+r)/2; if(d<=mid) lc[t]=built(lc[now],l,mid,d,v); else rc[t]=built(rc[now],mid+1,r,d,v); minn[t]=min(minn[lc[t]],minn[rc[t]]); return t; } int main() { // freopen("1.in","r",stdin); n=read(); minn[0]={n+1,0}; for(int i=1;i<=n;i++) { a[i]=read(); if(pos[a[i]]) { rt[i]=built(rt[i-1],1,n,pos[a[i]],n+1); rt[i]=built(rt[i],1,n,i,pos[a[i]]); } else rt[i]=built(rt[i-1],1,n,i,pos[a[i]]); pos[a[i]]=i; } for(int q=read();q;q--) { int l=read(),r=read(); pair<int,int>t=ask(rt[r],1,n,l,r); if(t.first<l) printf("%d\n",a[t.second]); else printf("0\n"); } }

考虑线段树 对于线段树上的节点,维护sum表示区间和,f1f2表示这个区间加上了以f1f2开头的"斐波那契数列"。 众所周知,Σfi=f[n+2]-f[2]那么在pushdown时,把f1f2下传到左儿子区间可以直接加过去,传到右儿子区间需要算一下新的f1f2。有了左右儿子区间的f1f2和区间长度,就可以算左右儿子区间加的sum了。 已知f1f2,求第n项是经典的矩阵快速幂,但是会T10。我看了网上题解后得知可以预处理出斐波那契数列每一项,然后O(1)询问第n项。 int sum[1200010],f1[1200010],f2[1200010],f[300010]; int n,m,mod=1000000009; // struct node // { // int v[3][3]; // friend node operator *(node a,node b) // { // node c; // for(int i=1;i<=2;i++) // { // for(int j=1;j<=2;j++) // { // c.v[i][j]=0; // for(int k=1;k<=2;k++) // c.v[i][j]=(c.v[i][j]+1ll*a.v[i][k]*b.v[k][j]%mod)%mod; // } // } // return c; // } // }; // int askf(int x,int F1,int F2) // { // x--; // node a,b; // a.v[1][1]=0; // a.v[1][2]=a.v[2][1]=a.v[2][2]=1; // b.v[1][1]=b.v[2][2]=1; // b.v[1][2]=b.v[2][1]=0; // while(x) // { // if(x&1) // b=b*a; // a=a*a; // x=x/2; // } // return (1ll*F1*b.v[1][1]+1ll*F2*b.v[1][2])%mod; // } int askf(int x,int F1,int F2) { if(x==1) return F1; return (1ll*F1*f[x-2]+1ll*F2*f[x-1])%mod; } void build(int x,int l,int r) { if(l==r) { sum[x]=read(); return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); sum[x]=(sum[x*2]+sum[x*2+1])%mod; } void pushdown(int x,int l,int r) { if(!f1[x]&&!f2[x]) return ; int mid=(l+r)/2; f1[x*2]=(f1[x*2]+f1[x])%mod; f2[x*2]=(f2[x*2]+f2[x])%mod; int f1r=askf(mid-l+2,f1[x],f2[x]); int f2r=askf(mid-l+3,f1[x],f2[x]); f1[x*2+1]=(f1[x*2+1]+f1r)%mod; f2[x*2+1]=(f2[x*2+1]+f2r)%mod; sum[x*2]=((sum[x*2]+f2r-f2[x])%mod+mod)%mod; sum[x*2+1]=((sum[x*2+1]+askf(r-mid+2,f1r,f2r)-f2r)%mod+mod)%mod; f1[x]=f2[x]=0; } void add(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) { sum[x]=((sum[x]+askf(r-l+3,f[l-tl+1],f[l-tl+2])-f[l-tl+2])%mod+mod)%mod; f1[x]=(f1[x]+f[l-tl+1])%mod; f2[x]=(f2[x]+f[l-tl+2])%mod; return ; } pushdown(x,l,r); int mid=(l+r)/2; if(tl<=mid) add(x*2,l,mid,tl,tr); if(tr>mid) add(x*2+1,mid+1,r,tl,tr); sum[x]=(sum[x*2]+sum[x*2+1])%mod; } int asksum(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return sum[x]; pushdown(x,l,r); int mid=(l+r)/2; if(tr<=mid) return asksum(x*2,l,mid,tl,tr); else if(tl>mid) return asksum(x*2+1,mid+1,r,tl,tr); else return (asksum(x*2,l,mid,tl,tr)+asksum(x*2+1,mid+1,r,tl,tr))%mod; } int main() { // freopen("1.in","r",stdin); f[1]=f[2]=1; for(int i=3;i<=300005;i++) f[i]=(f[i-1]+f[i-2])%mod; n=read();m=read(); build(1,1,n); for(;m;m--) { if(read()&1) { int tl=read(),tr=read(); add(1,1,n,tl,tr); } else { int tl=read(),tr=read(); printf("%d\n",asksum(1,1,n,tl,tr)); } } }

分层图 d[x][0/1][0/1]表示到x点,是否减过e[i].x,是否加过e[i].w 那么00状态可以转移到00,01,10,11 10状态可以转移到10,11 01状态可以转移到01,11 11状态可以转移到11 开始跑最短路即可 struct qy { ll d; int x,v1,v2; friend bool operator <(qy a,qy b) { return a.d>b.d; } }; priority_queue<qy>q; int n,m,v[200010][2][2]; ll d[200010][2][2]; vector<pair<int,int>>e[200010]; int main() { // freopen("1.in","r",stdin); n=read();m=read(); memset(d,0x3f,sizeof(d)); for(int i=1;i<=m;i++) { int x=read(),y=read(),w=read(); e[x].push_back({y,w}); e[y].push_back({x,w}); } d[1][0][0]=0; q.push({0,1,0,0}); while(q.size()) { int x=q.top().x,v1=q.top().v1,v2=q.top().v2; q.pop(); if(v[x][v1][v2])continue; v[x][v1][v2]=1; for(auto t:e[x]) { if(d[t.first][v1][v2]>d[x][v1][v2]+t.second) { d[t.first][v1][v2]=d[x][v1][v2]+t.second; q.push({d[t.first][v1][v2],t.first,v1,v2}); } } if(!v1&&!v2) { for(auto t:e[x]) { if(d[t.first][1][1]>d[x][0][0]+t.second) { d[t.first][1][1]=d[x][0][0]+t.second; q.push({d[t.first][1][1],t.first,1,1}); } } } if(!v1) { for(auto t:e[x]) { if(d[t.first][1][v2]>d[x][0][v2]) { d[t.first][1][v2]=d[x][0][v2]; q.push({d[t.first][1][v2],t.first,1,v2}); } } } if(!v2) { for(auto t:e[x]) { if(d[t.first][v1][1]>d[x][v1][0]+2*t.second) { d[t.first][v1][1]=d[x][v1][0]+2*t.second; q.push({d[t.first][v1][1],t.first,v1,1}); } } } } for(int i=2;i<=n;i++) printf("%lld ",d[i][1][1]); }

又是斜率优化dp f[i][j]=min(f[i][j],f[pre][j-1]+o[i]*(i-pre)-sum[i]+sum[pre]); 变化一下 f[i][j]-o[i]*i+sum[i]=min(f[pre][j-1]+sum[pre]-pre*o[i]) ll n,m,p; ll d[100010],o[100010],sum[100010],f[100010][110]; ll now[110]; struct ttt { ll x,f; }; vector<ttt>q[110]; int ask(ttt a,ttt b,ttt c) { return 1.0*(c.f-b.f)/(c.x-b.x)<=1.0*(b.f-a.f)/(b.x-a.x); } int main() { // freopen("1.in","r",stdin); n=read();m=read();p=read(); for(int i=2;i<=n;i++) d[i]=d[i-1]+read();//和一号的距离 for(int i=1;i<=m;i++) { int h=read(); int t=read(); o[i]=t-d[h];//这个时间出发的恰好能接到 } sort(o+1,o+1+m); for(int i=1;i<=m;i++) sum[i]=sum[i-1]+o[i];//前缀和 memset(f,0x3f,sizeof(f)); f[0][0]=0; q[0].push_back({0,0}); for(int j=1;j<=p;j++) for(int i=1;i<=m;i++) { while(now[j-1]+1<q[j-1].size()&&q[j-1][now[j-1]].f-o[i]*q[j-1][now[j-1]].x>q[j-1][now[j-1]+1].f-o[i]*q[j-1][now[j-1]+1].x) now[j-1]++; f[i][j]=q[j-1][now[j-1]].f-o[i]*q[j-1][now[j-1]].x+o[i]*i-sum[i]; while(q[j].size()>=2&&ask(q[j][q[j].size()-2],q[j][q[j].size()-1],{i,f[i][j]+sum[i]})) q[j].pop_back(); q[j].push_back({i,f[i][j]+sum[i]}); } cout<<f[m][p]; }

考虑线段树 如果区间颜色一样就直接修改,打懒标记 否则下传懒标记,进入下一层 复杂度不太懂啊 int now[400010]; ll sum[400010],lazy[400010]; void build(int x,int l,int r) { if(l==r) { now[x]=l; return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); } void pushdown(int x,int l,int r) { int mid=(l+r)/2; sum[x*2]+=1ll*(mid-l+1)*lazy[x]; sum[x*2+1]+=1ll*(r-mid)*lazy[x]; lazy[x*2]+=lazy[x]; lazy[x*2+1]+=lazy[x]; lazy[x]=0; now[x*2]=now[x*2+1]=now[x]; } void add(int x,int l,int r,int tl,int tr,int v) { if(tl<=l&&r<=tr&&now[x])//是一个颜色 { sum[x]+=1ll*(r-l+1)*abs(v-now[x]); lazy[x]+=abs(v-now[x]); now[x]=v; return ; } if(lazy[x]) pushdown(x,l,r); int mid=(l+r)/2; if(tl<=mid) add(x*2,l,mid,tl,tr,v); if(tr>mid) add(x*2+1,mid+1,r,tl,tr,v); sum[x]=sum[x*2]+sum[x*2+1]; if(now[x*2]==now[x*2+1]) now[x]=now[x*2]; else now[x]=0; } ll ask(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return sum[x]; if(lazy[x]) pushdown(x,l,r); int mid=(l+r)/2; ll t=0; if(tl<=mid) t+=ask(x*2,l,mid,tl,tr); if(tr>mid) t+=ask(x*2+1,mid+1,r,tl,tr); return t; } int main() { // freopen("1.in","r",stdin); int n=read(); build(1,1,n); for(int m=read();m;m--) { if(read()&1) { int l=read(),r=read(); add(1,1,n,l,r,read()); } else { int l=read(); printf("%lld\n",ask(1,1,n,l,read())); } } }

启发式合并,大胆开stl,map套set。 struct node { int k,i; }; vector<node>ask[100010]; string s[100010]; vector<int>e[100010]; int ans[100010],d[100010]; map<int,set<string>>o[100010]; void merge(int x,int y) { if(o[x].size()<o[y].size()) swap(o[x],o[y]); for(auto it:o[y]) for(auto i:it.second) o[x][it.first].insert(i); } void dfs(int x) { for(auto y:e[x]) { d[y]=d[x]+1; dfs(y); merge(x,y); } o[x][d[x]].insert(s[x]); for(auto i:ask[x]) ans[i.i]=o[x][i.k+d[x]].size(); } int main() { // freopen("1.in","r",stdin); int n=read(); for(int i=1;i<=n;i++) { cin>>s[i]; e[read()].push_back(i); } int m=read(); for(int i=1,v;i<=m;i++) { cin>>v; ask[v].push_back({read(),i}); } dfs(0); for(int i=1;i<=m;i++) printf("%d\n",ans[i]); }

好简单的题 线段树维护区间里4,7,47,74的最长子序列长度即可。 int n,m,f44[4000010],f77[4000010],f47[4000010],f74[4000010],lazy[4000010]; char s[1000010]; void build(int x,int l,int r) { if(l==r) { if(s[l]=='4') f44[x]=f74[x]=1; else f77[x]=f47[x]=1; return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); f44[x]=f44[x*2]+f44[x*2+1]; f77[x]=f77[x*2]+f77[x*2+1]; f47[x]=max(f44[x*2]+f47[x*2+1],max(f44[x*2]+f77[x*2+1],f47[x*2]+f77[x*2+1])); f74[x]=max(f77[x*2]+f74[x*2+1],max(f74[x*2]+f44[x*2+1],f44[x*2]+f44[x*2+1])); } void pushdown(int x) { swap(f44[x*2],f77[x*2]); swap(f47[x*2],f74[x*2]); swap(f44[x*2+1],f77[x*2+1]); swap(f47[x*2+1],f74[x*2+1]); lazy[x*2]^=1; lazy[x*2+1]^=1; lazy[x]=0; } void add(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) { swap(f44[x],f77[x]); swap(f47[x],f74[x]); lazy[x]^=1; return ; } if(lazy[x]) pushdown(x); int mid=(l+r)/2; if(tl<=mid) add(x*2,l,mid,tl,tr); if(tr>mid) add(x*2+1,mid+1,r,tl,tr); f44[x]=f44[x*2]+f44[x*2+1]; f77[x]=f77[x*2]+f77[x*2+1]; f47[x]=max(f44[x*2]+f47[x*2+1],max(f44[x*2]+f77[x*2+1],f47[x*2]+f77[x*2+1])); f74[x]=max(f77[x*2]+f74[x*2+1],max(f74[x*2]+f44[x*2+1],f44[x*2]+f44[x*2+1])); } int main() { // freopen("1.in","r",stdin); n=read();m=read(); scanf("%s",s+1); build(1,1,n); for(;m;m--) { scanf("%s",s); if(s[0]=='c') printf("%d\n",max(f44[1],f47[1])); else { int l=read(),r=read(); add(1,1,n,l,r); } } }

要算的是ΣC(n,r)*r^k 例如k=3,我们要求ΣC(n,r)*r^k 注意到长得很像(1+x)^n,等于ΣC(n,r)*x^r 现在对左右他求一次导再同时乘x nx(1+x)^(n-1)=ΣC(n,r)*r*x^r 再求一次导数 nx(1+x)^(n-1)+n(n-1)x^2(1+x)^(n-2)=ΣC(n,r)*r^2*x^r 再求一次导数 nx(1+x)^(n-1)+3*n*(n-1)*x^2*(1+x)^(n-2)+n*(n-1)*(n-2)x^3(1+x)^(n-3)=ΣC(n,r)*r^3*x^r 令x=1,令f[a][b]表示第a次求导时,x^b(1+x)^(n-b)的系数 那么求完三次导数,等式左边为 f[3][1]*x*(1+x)^(n-1)+f[3][2]*x^2*(1+x)^(n-2)+f[3][3]*x^3*(1+x)^(n-3) 等式右边是ΣC(n,r)*r^3*x^r,可以发现如果令x=1,即为所求 所以我们计算出Σf[k][i]*2^(n-i)即为所求 高等数学知识告诉我们,f[i][j]=f[i-1][j-1]*(n-j+1)+f[i-1][j]*j int f[5010][5010]; int n,k,ans,mod=1e9+7; int quick(ll x,int y) { ll t=1; while(y) { if(y&1) t=t*x%mod; x=x*x%mod; y=y/2; } return t; } int main() { n=read();k=read(); f[1][1]=n; for(int i=2;i<=k;i++) for(int j=1;j<=i;j++) f[i][j]=(1ll*f[i-1][j-1]*(n-j+1)+1ll*f[i-1][j]*j)%mod; int now=quick(2,n-1); int t=quick(2,mod-2); for(int i=1;i<=k;i++) { ans=(ans+1ll*f[k][i]*now)%mod; now=1ll*now*t%mod; } cout<<ans; }

https://www.cnblogs.com/chdy/p/17476439.html 用第二类斯特林数化简x^k 关键在于把ΣC(n,x)C(x,i)i!变成Σ2^(n-i)*n!/(n-i)! int s[5010][5010]; int n,k,ans,mod=1e9+7; int quick(ll x,int y) { ll t=1; while(y) { if(y&1) t=t*x%mod; x=x*x%mod; y=y/2; } return t; } int main() { n=read();k=read(); for(int i=1;i<=k;i++) for(int j=1;j<=i;j++) if(j==1) s[i][j]=1; else s[i][j]=(s[i-1][j-1]+1ll*j*s[i-1][j])%mod; int now=1ll*quick(2,n-1)*n%mod; int t=quick(2,mod-2); for(int i=1;i<=k;i++) { ans=(ans+1ll*s[k][i]*now)%mod; now=1ll*now*(n-i)%mod*t%mod; } cout<<ans; }

考虑dp 要记录的状态有到第几位了 i,有几个未关闭集合 j,已关闭的集合代价+未关闭的集合左端点到ai的距离和kk 那么答案是Σf[n][0][0-k] 对于i到i+1的转移 如果a[i+1]做左端点,那么j++,kk+=j*(a[i+1]-a[i]),方案数+=f[i][j][kk] 如果a[i+1]做右端点,那么j--,kk仍然+=那个,方案数+=f[i][j][kk]*j 若果a[i+1]做中间节点,那么j不变,kk仍然+=那个,方案数仍然+=f[i][j][kk]*j 如果a[i+1]自成一个集合,那么j不变,kk仍然+=那个,方案数+=f[i][j][kk] 如果ll f[210][210][1010]会越界,改成int或者滚动数组都可 int n,k; int a[210],mod=1e9+7; ll f[2][210][1010],ans; int main() { // freopen("1.in","r",stdin); n=read();k=read(); for(int i=1;i<=n;i++) a[i]=read(); sort(a+1,a+1+n); f[0][0][0]=1; for(int i=0;i<n;i++) { for(int j=0;j<=n;j++) for(int kk=0;kk<=k;kk++) f[i&1^1][j][kk]=0; for(int j=0;j<=n;j++) for(int kk=0;kk+j*(a[i+1]-a[i])<=k;kk++) { int t=kk+j*(a[i+1]-a[i]); f[i&1^1][j][t]=(f[i&1^1][j][t]+(1+j)*f[i&1][j][kk])%mod; f[i&1^1][j+1][t]=(f[i&1^1][j+1][t]+f[i&1][j][kk])%mod; if(j-1>=0) f[i&1^1][j-1][t]=(f[i&1^1][j-1][t]+f[i&1][j][kk]*j)%mod; } } for(int i=0;i<=k;i++) ans=(ans+f[n&1][0][i])%mod; cout<<ans; }

考虑暴力做法 从左往右,要把ai变bi 寻找右边第一次出现bi的位置r,对区间[i,r]排序,如果区间最小值等于bi就继续向右移动,否则输出no 具有一般性,对于ai是否等于bi都可以这样做,复杂度n方logn 考虑用queue和线段树加速 找第一次出现bi的位置r使用queue 线段树维护ai数组的区间最小值 每次用掉一个位置的就删掉 这样区间询问[i,r]就是询问所有未被删的ai的,r之前的最小值 判断[i,r]区间最小值是否为bi即可 queue<int>pos[300010]; int n,a[300010],b[300010],c[300010],d[300010]; int minn[1200010]; void build(int x,int l,int r) { if(l==r) { minn[x]=a[l]; return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); minn[x]=min(minn[x*2],minn[x*2+1]); } void add(int x,int l,int r,int d) { if(l==r) { minn[x]=400000; return ; } int mid=(l+r)/2; if(d<=mid) add(x*2,l,mid,d); else add(x*2+1,mid+1,r,d); minn[x]=min(minn[x*2],minn[x*2+1]); } int ask(int x,int l,int r,int tr) { if(r<=tr||minn[x]==400000) return minn[x]; int mid=(l+r)/2; if(tr<=mid) return ask(x*2,l,mid,tr); else return min(minn[x*2],ask(x*2+1,mid+1,r,tr)); } void work() { n=read(); for(int i=1;i<=n;i++) while(pos[i].size()) pos[i].pop(); for(int i=1;i<=n;i++) c[i]=a[i]=read(); for(int i=1;i<=n;i++) d[i]=b[i]=read(); sort(c+1,c+1+n); sort(d+1,d+1+n); for(int i=1;i<=n;i++) if(c[i]!=d[i]) { printf("NO\n"); return; } for(int i=1;i<=n;i++) pos[a[i]].push(i); build(1,1,n); for(int i=1;i<=n;i++) { int r=pos[b[i]].front(); pos[b[i]].pop(); if(ask(1,1,n,r)==b[i]) add(1,1,n,r); else { printf("NO\n"); return ; } } printf("YES\n"); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

考虑跑一个生成树,最多会留下来21个边,21个边涉及的点最多有42个 对着42个点跑floyd,再预处理一下42个点到每个点的距离 那么x到y要么是直接走生成树的边 要么先到42个点之一的i,再走到42个点之一的j,再走到y 复杂度42nlogn+q*42*42 (话说距离相关的数组用了好多) const int N=100010; int n,m; int fa[N][21],deep[N],a[50]; ll d[N],dis[50][50],dd[50][N]; int tot; vector<pair<int,int> >ee[N]; struct edge { int x,y; ll v; }e[30]; void dfs(int x) { for(auto y:ee[x]) { if(y.first==fa[x][0])continue; fa[y.first][0]=x; deep[y.first]=deep[x]+1; d[y.first]=d[x]+y.second; dfs(y.first); } } int get(int x) { return fa[x][0]==x?x:fa[x][0]=get(fa[x][0]); } ll lca(int x,int y) { ll t=d[x]+d[y]; if(deep[x]<deep[y]) swap(x,y); for(int i=20;i>=0;i--) if(deep[fa[x][i]]>=deep[y]) x=fa[x][i]; if(x==y) return t-2*d[x]; for(int i=20;i>=0;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; return t-2*d[fa[x][0]]; } int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) fa[i][0]=i; for(int i=1;i<=m;i++) { int x=read(),y=read(); ll v=read(); if(get(x)==get(y)) { tot++; e[tot]={x,y,v}; } else { fa[get(x)][0]=get(y); ee[x].push_back({y,v}); ee[y].push_back({x,v}); } } fa[1][0]=0; deep[1]=1; dfs(1); for(int i=1;i<=20;i++) for(int x=1;x<=n;x++) fa[x][i]=fa[fa[x][i-1]][i-1]; memset(dis,0x3f,sizeof(dis)); for(int i=1;i<=tot;i++) { a[i]=e[i].x; a[i+tot]=e[i].y; dis[i][i+tot]=dis[i+tot][i]=min(dis[i][i+tot],e[i].v); } tot=tot*2; for(int i=1;i<=tot;i++) for(int j=i;j<=tot;j++) dis[i][j]=dis[j][i]=min(dis[i][j],lca(a[i],a[j])); for(int i=1;i<=tot;i++) for(int j=1;j<=tot;j++) for(int k=1;k<=tot;k++) dis[j][k]=min(dis[j][k],dis[j][i]+dis[i][k]); for(int i=1;i<=tot;i++) for(int x=1;x<=n;x++) dd[i][x]=lca(a[i],x); for(int q=read();q;q--) { int x=read(),y=read(); ll ans=lca(x,y); for(int i=1;i<=tot;i++) for(int j=1;j<=tot;j++) ans=min(ans,dd[i][x]+dis[i][j]+dd[j][y]); printf("%lld\n",ans); } }

比如样例 3 2 1 2 3 那么把1 2 3 写成一个多项式 x+x^2+x^3 再求它的k次方 (x+x^2+x^3)^2=x^2+2*x^3+3*x^4+2*x^5+x^6 有系数的项的次数即为所求:2,3,4,5,6 用多项式乘法快速幂即可。因为次数越界了会造成一些错误(我不太懂啊),我加上了每次乘之后把系数降为1就过了。 #define rep(i,a,b) for(int i=(a);i<=(b);i++) #define per(i,a,b) for(int i=(a);i>=(b);i--) typedef double db; typedef long long ll; struct cp { db x,y; cp(db real=0,db imag=0):x(real),y(imag){}; cp operator +(cp b)const{return {x+b.x,y+b.y};} cp operator -(cp b)const{return {x-b.x,y-b.y};} cp operator*(cp b)const{return {x*b.x-y*b.y,x*b.y+y*b.x};} }; using vcp=vector<cp>; using Poly=vector<int>; class Cipolla { int P,I2{}; using pll=pair<ll,ll>; }; #define MUL(a,b) (ll(a)*(b)%P) #define ADD(a,b) (((a)+=(b))>=P?(a)-=P:0) #define SUB(a,b) (((a)-=(b))<0?9a)+=P:0) const int P=1e9+7,N=2e5+10; namespace FFT{ const db pi=acos(-1); vcp Omega(int L){ vcp w(L);w[1]=1; for(int i=2;i<L;i<<=1){ auto w0=w.begin()+i/2,w1=w.begin()+i; cp wn(cos(pi/i),sin(pi/i)); for(int j=0;j<i;j+=2) w1[j]=w0[j>>1],w1[j+1]=w1[j]*wn; } return w ; } auto W=Omega(1<<21); void DIF(cp *a,int n){ cp x,y; for(int k=n>>1;k;k>>=1) for(int i=0;i<n;i+=k<<1) for(int j=0;j<k;j++) x=a[i+j],y=a[i+j+k],a[i+j+k]=(a[i+j]-y)*W[k+j],a[i+j]=x+y; } void IDIT(cp *a,int n){ cp x,y; for(int k=1;k<n;k<<=1) for(int i=0;i<n;i+=k<<1) for(int j=0;j<k;j++) x=a[i+j],y=a[i+j+k]*W[k+j],a[i+j+k]=x-y,a[i+j]=x+y; const db Inv=1. /n; rep(i,0,n-1)a[i].x*=Inv,a[i].y*=Inv; reverse(a+1,a+n); } } namespace Polynomial{ void DFT(vcp &a){FFT::DIF(a.data(),a.size());} void IDFT(vcp &a){FFT::IDIT(a.data(),a.size());} int norm(int n){return 1<<(__lg(n-1)+1);} void norm(Poly &a){if(!a.empty())a.resize(norm(a.size()),0); else a={0};} vcp &dot(vcp &a,vcp &b){rep(i,0,a.size()-1)a[i]=a[i]*b[i]; return a;} Poly operator *(ll k,Poly a){ Poly ans; for(auto i:a) ans.push_back(k*i); return ans; } Poly operator *(Poly a,Poly b){ int n=a.size()+b.size()-1; vcp c(norm(n)); rep(i,0,a.size()-1)c[i].x=a[i]; rep(i,0,b.size()-1)c[i].y=b[i]; DFT(c),dot(c,c),IDFT(c),a.resize(n); rep(i,0,n-1)a[i]=(int)(c[i].y*.5+.5); return a; } } using namespace Polynomial; int a[1010]; int main() { // freopen("1.in","r",stdin); // freopen("1.out","w",stdout); int n=read(),k=read(); for(int i=1;i<=n;i++) a[i]=read(); sort(a+1,a+1+n); Poly vec(a[n]+1),t; for(int i=1;i<=n;i++) vec[a[i]]=1; Poly ans=vec; k--; while(k) { if(k&1) { ans=ans*vec; for(int i=0;i<ans.size();i++) if(ans[i]) ans[i]=1; } vec=vec*vec; k=k/2; for(int i=0;i<vec.size();i++) if(vec[i]) vec[i]=1; } for(int i=1;i<ans.size();i++) if(ans[i]) printf("%d ",i); }

暴力的dp:f[i]=max(f[j]+max(a[j+1]...a[i])-min(a[j+1]...a[i]) 考虑从i到1的max是单调增的,单调栈记录一下这些增大的节点,如果ai使前面的推栈了就更新区间值。min也相同地处理 int n,a[1000010],axx,inn; ll f[1000010],c[4000010],lazy[4000010]; vector<pair<int,int>>maxx,minn; void pushdown(int x) { if(lazy[x]) { lazy[x*2]+=lazy[x]; lazy[x*2+1]+=lazy[x]; c[x*2]+=lazy[x]; c[x*2+1]+=lazy[x]; lazy[x]=0; } } void add(int x,int l,int r,int tl,int tr,ll v) { if(tl<=l&&r<=tr) { c[x]+=v; lazy[x]+=v; return ; } pushdown(x); int mid=(l+r)/2; if(tl<=mid) add(x*2,l,mid,tl,tr,v); if(tr>mid) add(x*2+1,mid+1,r,tl,tr,v); c[x]=max(c[x*2],c[x*2+1]); } int main() { // freopen("1.in","r",stdin); n=read(); // for(int i=1;i<=n;i++) // { // a[i]=read(); // int minn=a[i],maxx=a[i]; // for(int j=i-1;j>=0;j--) // { // f[i]=max(f[i],f[j]+maxx-minn); // minn=min(minn,a[j]); // maxx=max(maxx,a[j]); // } // } maxx.push_back({2e9,0}); minn.push_back({-2e9,0}); for(int i=1;i<=n;i++) { a[i]=read(); while(maxx[axx].first<a[i]) { add(1,0,n,maxx[axx-1].second,maxx[axx].second-1,a[i]-maxx[axx].first); maxx.pop_back(); axx--; } while(minn[inn].first>a[i]) { add(1,0,n,minn[inn-1].second,minn[inn].second-1,minn[inn].first-a[i]); minn.pop_back(); inn--; } f[i]=c[1]; add(1,0,n,i,i,f[i]); maxx.push_back({a[i],i}); minn.push_back({a[i],i}); axx++; inn++; } cout<<f[n]; }

浅显的做法是nlog^3,用调和级数+二分+主席树,主席树维护区间里pre都落在了哪。显然是会超时的 int tot,lc[2000000],rc[2000000],c[2000000],pre[100010],rt[100010],n; int build(int x,int l,int r,int d) { tot++; int t=tot; lc[t]=lc[x]; rc[t]=rc[x]; c[t]=c[x]+1; if(l==r) return t; int mid=(l+r)/2; if(d<=mid) lc[t]=build(lc[x],l,mid,d); else rc[t]=build(rc[x],mid+1,r,d); return t; } int ask(int x1,int x2,int l,int r,int tl,int tr) { if(x1==0&&x2==0||tl<=l&&r<=tr) return c[x2]-c[x1]; int mid=(l+r)/2; if(tr<=mid) return ask(lc[x1],lc[x2],l,mid,tl,tr); else if(tl>mid) return ask(rc[x1],rc[x2],mid+1,r,tl,tr); else return ask(lc[x1],lc[x2],l,mid,tl,tr)+ask(rc[x1],rc[x2],mid+1,r,tl,tr); } int ask(int x,int k) { int l=x,r=n,mid; while(l+1<r) { mid=(l+r)/2; if(ask(rt[x-1],rt[mid],0,n,0,x-1)>k)//区间x到mid有多少个pre落在0到x-1 r=mid; else l=mid; } if(ask(rt[x-1],rt[r],0,n,0,x-1)<=k) return r; return l; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { int x=read(); rt[i]=build(rt[i-1],0,n,pre[x]); pre[x]=i; } for(int k=1;k<=n;k++) { int ans=0; for(int i=1;i<=n;i=ask(i,k)+1) ans++; printf("%d ",ans); } } 考虑把主席树维护的东西反过来,维护落在i上的pre都从哪来。那么就可以主席树上二分了。我只会求第一个等于k的pos,所以求第一个等于k+1的pos再减一就是最后一个等于k的pos了。复杂度nlog^2,调和级数+主席树上二分。 int tot,lc[2000000],rc[2000000],c[2000000],pre[100010],rt[100010],n; queue<int>pos[100010]; int build(int x,int l,int r,int d) { tot++; int t=tot; lc[t]=lc[x]; rc[t]=rc[x]; c[t]=c[x]+1; if(l==r) return t; int mid=(l+r)/2; if(d<=mid) lc[t]=build(lc[x],l,mid,d); else rc[t]=build(rc[x],mid+1,r,d); return t; } int ask(int x1,int x2,int l,int r,int tl,int tr) { if(x1==0&&x2==0||tl<=l&&r<=tr) return c[x2]-c[x1]; int mid=(l+r)/2; if(tr<=mid) return ask(lc[x1],lc[x2],l,mid,tl,tr); else if(tl>mid) return ask(rc[x1],rc[x2],mid+1,r,tl,tr); else return ask(lc[x1],lc[x2],l,mid,tl,tr)+ask(rc[x1],rc[x2],mid+1,r,tl,tr); } void build0(int x,int l,int r) { if(l==r) { if(pos[0].size()&&l==pos[0].front()) c[x]=1,pos[0].pop(); return ; } int mid=(l+r)/2; tot++; lc[x]=tot; tot++; rc[x]=tot; build0(lc[x],l,mid); build0(rc[x],mid+1,r); c[x]=c[lc[x]]+c[rc[x]]; } int askpos(int x,int l,int r,int k) { if(l==r) return l; int mid=(l+r)/2; if(c[lc[x]]>=k) return askpos(lc[x],l,mid,k); else return askpos(rc[x],mid+1,r,k-c[lc[x]]); } int askc(int x,int l,int r,int d) { if(r<=d) return c[x]; int mid=(l+r)/2; if(d<=mid) return askc(lc[x],l,mid,d); else return c[lc[x]]+askc(rc[x],mid+1,r,d); } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { int x=read(); pos[pre[x]].push(i); pre[x]=i; } tot++; build0(1,1,n+1); rt[0]=1; for(int i=1;i<=n;i++) { if(pos[i].size()==0) { rt[i]=rt[i-1]; continue; } rt[i]=build(rt[i-1],1,n+1,pos[i].front()); } for(int k=1;k<=n;k++) { int ans=0; for(int i=1;i<=n;) { ans++; i=askpos(rt[i-1],1,n+1,k+askc(rt[i-1],1,n+1,i)); } printf("%d ",ans); } }

挺正常的树形dp 考虑b比较大不能背包,可以维护f[x][i][0/1]表示在x的子树中买了i个商品,x是否用了优惠 从上往下dp,才不会重复计算 以及f数组开ll 时间复杂度是Σsiz[y]*Σsiz[比我先来的兄弟子树],是小于n^2的 int n,b; int d[5010],c[5010],siz[5010]; ll f[5010][5010][2]; vector<int>e[5010]; void dfs(int x) { f[x][0][0]=0; f[x][1][0]=d[x]; f[x][1][1]=d[x]-c[x]; siz[x]=1; for(auto y:e[x]) { dfs(y); for(int i=siz[x];i>=0;i--) for(int j=siz[y];j>=1;j--) { f[x][i+j][0]=min(f[x][i+j][0],f[x][i][0]+f[y][j][0]); f[x][i+j][1]=min(f[x][i+j][1],f[x][i][1]+min(f[y][j][1],f[y][j][0])); } siz[x]+=siz[y]; } } int main() { // freopen("1.in","r",stdin); n=read();b=read(); d[1]=read();c[1]=read(); for(int i=2;i<=n;i++) { d[i]=read();c[i]=read(); e[read()].push_back(i); } memset(f,0x3f,sizeof(f)); dfs(1); for(int i=n;i>=0;i--) if(f[1][i][0]<=b||f[1][i][1]<=b) { cout<<i; return 0; } }

从大往小考虑 如果他需要i个人就会投我票,但是人数已经大于了i,那么就可以先放放 具体体现在继续留在堆里 priority_queue<int,vector<int>,greater<int>>q; vector<int>o[200010]; int n; ll ans; void work() { n=read();ans=0; while(q.size())q.pop(); for(int i=0;i<=n;i++) o[i].clear(); for(int i=1;i<=n;i++) { int m=read(); o[m].push_back(read()); } for(int i=n;i>=0;i--) { for(auto x:o[i]) q.push(x); while(q.size()>n-i) { ans+=q.top(); q.pop(); } } printf("%lld\n",ans); } int main() { for(int t=read();t;t--) work(); }

考虑如果没有横贯整个区域的线段 那么每个线段之间的交点都会多产生一个区域 但是如果每多加一个l=0,r=1e6的线段,区域也会加一 所以答案为1+(l=0&&r=1e6)线段数量+线段交点数量,是经典问题,2023ccpc河南省赛I题就考过,可以用线段树或者主席树搞一搞。 int n,m; vector<int>jia[1000010],jian[1000010]; ll ans; int c[4000010]; struct node { int x,l,r; friend bool operator <(node a,node b) { return a.x<b.x; } }o[100010]; void add(int x,int l,int r,int d,int v) { c[x]+=v; if(l==r) return ; int mid=(l+r)/2; if(d<=mid) add(x*2,l,mid,d,v); else add(x*2+1,mid+1,r,d,v); } int ask(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return c[x]; int mid=(l+r)/2; if(tr<=mid) return ask(x*2,l,mid,tl,tr); else if(tl>mid) return ask(x*2+1,mid+1,r,tl,tr); else return ask(x*2,l,mid,tl,tr)+ask(x*2+1,mid+1,r,tl,tr); } int main() { // freopen("1.in","r",stdin); n=read();m=read(); ans=1; for(int i=1;i<=n;i++) { int y=read(),l=read(),r=read(); jia[l].push_back(y); jian[r].push_back(y); if(l==0&&r==1000000) ans++; } for(int i=1;i<=m;i++) { o[i].x=read(); o[i].l=read(); o[i].r=read(); if(o[i].l==0&&o[i].r==1000000) ans++; } sort(o+1,o+1+m); for(auto x:jia[0]) add(1,1,1000000,x,1); for(int i=1;i<=m;i++) { for(int j=o[i-1].x+1;j<=o[i].x;j++) for(auto x:jia[j]) add(1,1,1000000,x,1); for(int j=o[i-1].x;j<o[i].x;j++) for(auto x:jian[j]) add(1,1,1000000,x,-1); ans+=ask(1,1,1000000,o[i].l,o[i].r); } cout<<ans; }

打得我道心破碎 考虑左端点从右往左移动,每个右端点的贡献不断增大,且随着右端点增大而增大。 所以用线段树维护区间里最小最大值,那么区间是同一个值当且仅当minn==maxx,区间恰好是单调上升的区间当且仅当maxx-minn==r-l 只对这种区间修改,否则暴力递归左右子区间即可。 int n; ll now,ans; char s[500010]; int maxx[2000010],minn[2000010]; int lmax[2000010],lmin[2000010]; void pushdown(int x,int l,int r) { if(lmin[x]==lmax[x]) lmin[x*2]=minn[x*2]=lmax[x*2]=maxx[x*2]=lmin[x*2+1]=minn[x*2+1]=lmax[x*2+1]=maxx[x*2+1]=lmin[x]; else lmin[x*2]=minn[x*2]=lmin[x],lmin[x*2+1]=minn[x*2+1]=lmin[x]+r-l, lmax[x*2]=maxx[x*2]=lmin[x*2+1]-1,lmax[x*2+1]=maxx[x*2+1]=lmax[x]; lmax[x]=lmin[x]=0; } void add1(int x,int l,int r,int tl,int tr,int v) { if(tl<=l&&minn[x]>=v-tl+l) return ; if(tl<=l&&r<=tr) { if(minn[x]==maxx[x]||r-l==maxx[x]-minn[x])//区间为一个值 { v=v-tl+l; now=now+1ll*(v+v+r-l-maxx[x]-minn[x])*(r-l+1)/2; minn[x]=lmin[x]=v;//懒标记 maxx[x]=lmax[x]=v+r-l; return ; } } int mid=(l+r)/2; if(lmax[x]!=0) pushdown(x,l,mid+1); if(tl<=mid) add1(x*2,l,mid,tl,tr,v); if(tr>mid) add1(x*2+1,mid+1,r,tl,tr,v); minn[x]=minn[x*2]; maxx[x]=maxx[x*2+1]; } void add2(int x,int l,int r,int tl,int v) { if(minn[x]>=v) return ; if(tl<=l) { if(minn[x]==maxx[x]||r-l==maxx[x]-minn[x]&&maxx[x]<=v)//区间为一个值 { now=now+1ll*v*(r-l+1)-1ll*(maxx[x]+minn[x])*(r-l+1)/2; lmax[x]=lmin[x]=maxx[x]=minn[x]=v;//懒标记 return ; } } int mid=(l+r)/2; if(lmax[x]!=0) pushdown(x,l,mid+1); if(tl<=mid) add2(x*2,l,mid,tl,v); add2(x*2+1,mid+1,r,tl,v); minn[x]=minn[x*2]; maxx[x]=maxx[x*2+1]; } int main() { // freopen("1.in","r",stdin); n=read(); scanf("%s",s+1); for(int i=n,len=0;i>=1;i--) { if(s[i]=='0') { ans+=now; len=0; continue; } len++; if(i+len<=n) add2(1,1,n,i+len,len); add1(1,1,n,i,i+len-1,1); ans+=now; } cout<<ans; }

注意到任意k满足条件,则2k,4k,8k也满足条件(这些k的倍数小于等于n时 所以只考虑n/2+1这些长度即可 假如长为7 则需考虑4567长度 4长度时,区间和设为s,s+x-a1,s+2x-a1-a2,s+3x-a1-a2-a3 5长度时,区间和为s+x,s+2x-a1,s+3x-a1-a2 6长度时,区间和为s+2x,s+3x-a1 7长度时,区间和为s+3x 要做的是枚举长度,看看最小区间和是否大于0 注意到每次k增大时,最后一个区间和会被踢掉,其他区间同时加x 所以考虑把区间长度是n/2+1时的区间和带着左端点的信息,扔到小根堆里 对于长度增加要踢掉的区间和,不在考虑范围内,可以一个while循环踢掉 然后判断这个最小值+偏移量是否大于0即可 int read() { int x;scanf("%d",&x);return x; } priority_queue<pair<ll,int>,vector<pair<ll,int>>,greater<pair<ll,int>>>q; ll sum,x; int n,t,a[500010]; int main() { // freopen("1.in","r",stdin); n=read(); t=n/2+1; for(int i=1;i<=t;i++) sum+=(a[i]=read()); x=read(); q.push({sum,1}); for(int i=t+1;i<=n;i++) { sum=sum+x-a[i-t]; q.push({sum,i-t+1}); } for(int k=t,i=n-t+1;k<=n;k++,i--) { while(q.top().second>i) q.pop(); if(q.top().first+(k-t)*x>0) { cout<<k; return 0; } } cout<<-1; }

不会,抄的https://blog.csdn.net/LBCLZMB/article/details/107503613 int n,m,w[200010],d[200010],v[200010],ok[200010]; vector<pair<int,int>>e[200010]; queue<int>q; stack<int>ans; int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) w[i]=read(); for(int i=1;i<=m;i++) { int x=read(),y=read(); d[x]++; d[y]++; e[x].push_back({y,i}); e[y].push_back({x,i}); } for(int i=1;i<=n;i++) if(w[i]>=d[i]) { q.push(i); v[i]=1; } while(q.size()) { int x=q.front();q.pop(); for(auto y:e[x]) { if(!ok[y.second]) { ans.push(y.second); ok[y.second]=1; } } for(auto y:e[x]) { d[y.first]--; if(w[y.first]>=d[y.first]) { if(!v[y.first]) q.push(y.first),v[y.first]=1; } } } if(ans.size()==m) { printf("ALIVE\n"); while(ans.size()) printf("%d ",ans.top()),ans.pop(); } else printf("DEAD"); }

考虑记忆化区间dp f[l][r][res]表示刚到这个区间,带着res的和l相同的来的 那么如果l==r,不得不计算代价为a[res+len[l]] 否则要么拿分,再往后走,a[res+len[l]]+ask(l+1,r,0) 要么把res+len[l]拖到后面,ask(l+1,j-1,0)+ask(j,r,res+len[l]) 取max即可 int n,tot,len[110]; char s[110]; int v[110][110][110]; ll f[110][110][110],a[110]; ll ask(int l,int r,int res) { if(v[l][r][res]) return f[l][r][res]; v[l][r][res]=1; if(l==r) return f[l][r][res]=a[res+len[l]]; f[l][r][res]=a[res+len[l]]+ask(l+1,r,0);//先拿下再往后走 for(int j=l+2;j<=r;j+=2) f[l][r][res]=max(f[l][r][res],ask(l+1,j-1,0)+ask(j,r,res+len[l]));//先往后走再一块吃 return f[l][r][res]; } int main() { // freopen("1.in","r",stdin); n=read(); scanf("%s",s+1); for(int i=1;i<=n;i++) { tot++; len[tot]=1; while(s[i+1]==s[i]) { len[tot]++; i++; } } for(int i=1;i<=n;i++) { a[i]=max(a[i],read()); for(int j=i;j<=n;j++) a[j]=max(a[j],a[j-i]+a[i]); } cout<<ask(1,tot,0); }

会有(n+1)/2认同答案,所以大胆随机取20个人,计算他的子集。答案不在这20个人的子集里的概率非常小。 那么问题转变成对于一个人的2^15的子集,计算每个子集出现的次数,判断是否大于等于(n+1)/2。我感觉很眼熟,想了半天想起来就是这篇博客上面,449D的同款问题。 vector<int>pos[200010]; int n,m,p,f[200010]; ll val[200010],maxx,ans; char s[100]; int ask(int x) { int sum=0; while(x) { sum=sum+(x&1); x=x/2; } return sum; } void work(int x) { int k=pos[x].size(); for(int i=0;i<(1<<(k+1));i++) f[i]=0; for(int i=1;i<=n;i++) { int t=0; for(int j=0;j<k;j++) if(val[i]&(1ll<<pos[x][j])) t=t*2+1; else t=t*2; f[t]++; } for(int j=0;j<=k;j++) for(int i=0;i<(1<<k);i++) if((i&(1<<j))==0) f[i]=f[i]+f[i+(1<<j)]; for(int i=0;i<(1<<k);i++) if(f[i]>=(n+1)/2&&ask(i)>maxx) { maxx=ask(i); ans=0; for(int j=k-1;j>=0;j--) if(i&(1<<j)) ans=ans+(1ll<<pos[x][k-j-1]); } } int main() { // freopen("1.in","r",stdin); srand(time(0)); n=read(); m=read(); p=read(); for(int i=1;i<=n;i++) { scanf("%s",s+1); for(int j=1;j<=m;j++) { val[i]=val[i]*2+s[j]-'0'; if(s[j]=='1') pos[i].push_back(m-j); } } for(int t=1;t<=20;t++) work(1ll*rand()*rand()%n+1); for(int i=m-1;i>=0;i--) cout<<bool(ans&(1ll<<i)); }

一点不会,抄的题解 int n,m,a[10010],vis[10010][1010],d[10010][1010]; deque<pair<int,int>>q; ll g,r; int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=m;i++) a[i]=read(); a[m+1]=n; sort(a+0,a+1+m+1); g=read();r=read(); q.push_back({0,0}); vis[0][0]=1; ll ans=-1; while(q.size()) { int x=q.front().first; int t=q.front().second; q.pop_front(); if(t==0) { int to=n-a[x]; if(to<=g) { if(ans==-1||ans>(r+g)*d[x][t]+to) ans=(r+g)*d[x][t]+to; } } if(t==g) { if(vis[x][0]==0) { d[x][0]=d[x][t]+1; q.push_back({x,0}); vis[x][0]=1; } continue; } if(x) { int to=t+a[x]-a[x-1]; if(to<=g&&vis[x-1][to]==0) { vis[x-1][to]=1; d[x-1][to]=d[x][t]; q.push_front({x-1,to}); } } if(x<m-1) { int to=t+a[x+1]-a[x]; if(to<=g&&vis[x+1][to]==0) { vis[x+1][to]=1; d[x+1][to]=d[x][t]; q.push_front({x+1,to}); } } } cout<<ans; }

考虑每次加点x和y,直径改变最多只会改变一个端点到x或者y。 所以先把树建一下,准备lca。然后扫一下修改操作,大胆更新。因为加点xy时只会有一个变成直径的端点,所以只用x判断一下即可。 #include<bits/stdc++.h> using namespace std; typedef long long ll; int read() { int x;scanf("%d",&x);return x; } vector<int>e[1000010]; int fa[1000010][25],n,d[1000010]; void dfs(int x) { for(auto y:e[x]) { fa[y][0]=x; d[y]=d[x]+1; dfs(y); } } int lca(int x,int y) { int t=d[x]+d[y]; if(d[x]>d[y]) swap(x,y); for(int i=21;i>=0;i--) if(d[fa[y][i]]>=d[x]) y=fa[y][i]; if(x==y) return t-2*d[y]; for(int i=21;i>=0;i--) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; return t-2*d[fa[x][0]]; } int main() { // freopen("1.in","r",stdin); n=read(); e[1].push_back(2); e[1].push_back(3); e[1].push_back(4); for(int i=1,x=5,y=6;i<=n;x+=2,y+=2,i++) { int t=read(); e[t].push_back(x); e[t].push_back(y); } dfs(1); for(int i=1;i<=21;i++) for(int x=1;x<=4+2*n;x++) fa[x][i]=fa[fa[x][i-1]][i-1]; int ans=2,l=2,r=3; for(int i=1,x=5,y=6;i<=n;i++,x+=2,y+=2) { int dl=lca(x,l); int dr=lca(x,r); if(ans<=dr&&dl<=dr) { l=x; ans=dr; } else if(ans<=dl&&dr<=dl) { r=x; ans=dl; } printf("%d\n",ans); } }

看了好多个题解,都没看懂,逐渐怀疑人生。于是按我的想法写了写就过了。 首先写一个显然能优化的n^4的复杂度的dp:f[i][x][y]=1表示到了第i个果树之后,能剩下x个红的,y个绿的。那么最后枚举f[n][x][y],如果为1,则更新答案为max(ans,(sum-x-y)/k)。 那么dp的时候,枚举第i个果树,有l个红的和k-l个绿的组合了,这需要l<=a[i]并且0<=k-l<=b[i],那么还剩a[i]-l个红的,b[i]-k+l个绿的,f[i][x][y]可以转移到f[i][(x+a[i]-l)%k][(y+b[i]-(k-l)%k)%k]上面。 ll n,k,ans,sum; bool f[510][510][510]; ll a[510],b[510]; int main() { // freopen("1.in","r",stdin); n=read();k=read(); f[0][0][0]=1; for(int i=1;i<=n;i++) { a[i]=read();b[i]=read(); sum+=a[i]+b[i]; } for(int i=1;i<=n;i++) for(int x=0;x<k;x++) for(int y=0;y<k;y++) { if(f[i-1][x][y]==0) continue; for(int l=0;l<=min(k,a[i]);l++) if((k-l)%k<=b[i]) f[i][(x+a[i]-l)%k][(y+b[i]-(k-l)%k)%k]=1; } for(int x=0;x<k;x++) for(int y=0;y<k;y++) if(f[n][x][y]) ans=max(ans,(sum-x-y)/k); cout<<ans; } 这个代码果然超时了,T33,于是心满意足地去优化。 考虑到x和y的关系:f[i][x][y]是合法的当且仅当y=(a1+a2+...ai-x)%k,于是显然可以省略掉一个循环。 ll n,k,ans,sum,tsum; // bool f[510][510][510]; bool f[510][510]; ll a[510],b[510]; int main() { // freopen("1.in","r",stdin); n=read();k=read(); // f[0][0][0]=1; f[0][0]=1; for(int i=1;i<=n;i++) { a[i]=read();b[i]=read(); sum+=a[i]+b[i]; } for(int i=1;i<=n;i++) { tsum=(tsum+a[i]+b[i])%k; for(int x=0;x<k;x++) { // int y=(tsum-x+k)%k; // for(int y=0;y<k;y++) { // if(f[i-1][x][y]==0) if(f[i-1][x]==0) continue; for(int l=0;l<=min(k,a[i]);l++) if((k-l)%k<=b[i]) { // f[i][(x+a[i]-l)%k][(y+b[i]-(k-l)%k)%k]=1; f[i][(x+a[i]-l)%k]=1; } } } } for(int x=0;x<k;x++) { int y=(tsum-x+k)%k; // for(int y=0;y<k;y++) // if(f[n][x][y]) if(f[n][x]) ans=max(ans,(sum-x-y)/k); } cout<<ans; }

感觉难在实现 考虑现在要把一个连通块判定是否是一个fib树 设为第k项,则需要把它分为一块k-1,一块k-2 注意到k-1还可以分出来k-2和k-3 所以遇到子树大小为k-1或者k-2直接切断即可 代码实现时,把边定义vector<pair<int,bool>>,为对xy切断时遍历x的边,遇到y让bool=1。遍历y的边,遇到x让bool等于1。之后递归地判断xy所在连通块是否是fib树。 vector<pair<int,bool>>G[200010]; int n,siz[200010]; vector<int>fib; void NO() { printf("NO"); exit(0); } void getsiz(int u,int fa) { siz[u]=1; for(auto e:G[u]) { if(e.second)continue; int v=e.first; if(v==fa)continue; getsiz(v,u); siz[u]+=siz[v]; } } void cutedge(int u,int fa,int k,int &pu,int &pv,int &kd) { for(auto e:G[u]) { if(pu)return ; if(e.second)continue; int v=e.first; if(v==fa) continue; if(siz[v]==fib[k-1]||siz[v]==fib[k-2]) { pu=u,pv=v; kd=(siz[v]==fib[k-1])?k-1:k-2; break; } cutedge(v,u,k,pu,pv,kd); } } void check(int u,int k) { if(k<=1)return ; getsiz(u,0); int pu=0,pv=0,kd=0; cutedge(u,0,k,pu,pv,kd); if(!pu) NO(); for(auto &e:G[pu]) if(e.first==pv) e.second=true; for(auto &e:G[pv]) if(e.first==pu) e.second=true; check(pv,kd); check(pu,kd==k-1?k-2:k-1); } int main() { cin>>n; fib.push_back(1); fib.push_back(1); for(int i=1;fib[i]<n;i++) fib.push_back(fib[i]+fib[i-1]); for(int i=1;i<n;i++) { int u,v; cin>>u>>v; G[u].push_back({v,0}); G[v].push_back({u,0}); } if(fib[fib.size()-1]!=n) NO(); check(1,fib.size()-1); cout<<"YES"; }

首先写了一个暴力代码找规律,可以发现对n=5,sum相同时,稳定状态也相同。 而且是一个等差数列,但是可能存在一个位置相同。 int n,a[1000],b[1000]; int main() { n=5; for(int kkk=5;kkk<=30;kkk++) { for(int i=1;i<n;i++) a[i]=i; a[n]=kkk; while(1) { int flag=0; for(int i=1;i<n;i++) if(a[i]+2<=a[i+1]) flag=1; if(!flag) break; for(int i=1;i<=n;i++) { if(i!=1&&a[i-1]+2<=a[i]&&a[i]+2<=a[i+1]) b[i]=a[i]; else if(i!=1&&a[i-1]+2<=a[i]) b[i]=a[i]-1; else if(a[i]+2<=a[i+1]) b[i]=a[i]+1; else b[i]=a[i]; } for(int i=1;i<=n;i++) a[i]=b[i]; } for(int i=1;i<=n;i++) cout<<a[i]<<' '; cout<<endl; } } 考虑对每个位置二分答案,寻找最后一个满足x+(x+x+n-2)*(n-1)/2<=sum的值,即为ai 每次求出ai后让n--,sum-=ai ll ask(ll n,ll sum) { ll l=0,r=1e12,mid; while(l+1<r) { mid=(l+r)/2; if(mid+(mid+mid+n-2)*(n-1)/2>sum) r=mid; else l=mid; } if(r+(r+r+n-2)*(n-1)/2<=sum) return r; return l; } int n; ll sum; int main() { n=read(); for(int i=1;i<=n;i++) sum+=read(); for(int i=1;i<=n;i++) { ll ai=ask(n-i+1,sum); sum-=ai; cout<<ai<<' '; } }

镇难啊 考虑把最大值放在第一个,这样只允许1走1-n,走到后面,而2、3、4都不能走1-n这条边。 接下来从后往前,维护一个单调栈,再用线段树维护单调栈里面有哪些值 那么对于i及i以后的单调栈,可以用于计算以i-1为左端点的区间数量 如果a[i-1]>=a[i],则ans+=min(单调栈里元素数量,单调栈里小于等于a[i-1]的数字数量+1),既一个允许向下一次,立刻向上的圆弧,并允许往上走一下 例如5 2 3 4 5 6,以第一个5为左端点,所有的其他数字都可以做右端点。 如果a[i-1]<a[i],则只允许向右走一下子,ans++ 例如5 6 1 2 3 7,以5为左端点,只允许以6为右端点 除此之外,作为a[1]的最大值有可能走到后面 例如5 2 3 4 3 2,以1为左端点,正着看有52,523,5234。但是走1-n的52,523就会没有记入答案。再从后往前跑一遍即可。 int n,m; int b[1000010],a[1000010],c[4000010];//离散化数组与原数组与线段树数组 int vis[1000010]; vector<int>o[1000010]; stack<pair<int,int>>q; ll ans; void add(int x,int l,int r,int p,int v) { c[x]+=v; if(l==r) return ; int mid=(l+r)/2; if(p<=mid) add(x*2,l,mid,p,v); else add(x*2+1,mid+1,r,p,v); } int ask(int x,int l,int r,int v)//小于等于v的数量 { if(v>=r) return c[x]; int mid=(l+r)/2; if(v>mid) return c[x*2]+ask(x*2+1,mid+1,r,v); else return ask(x*2,l,mid,v); } int main() { // freopen("1.in","r",stdin); // freopen("1.out","w",stdout); n=read(); for(int i=1;i<=n;i++) b[i]=read(); int maxx=1; for(int i=1;i<=n;i++) if(b[i]>b[maxx]) maxx=i; for(int i=maxx;i<=n;i++) a[i-maxx+1]=b[i]; for(int i=1;i<maxx;i++) a[i+n-maxx+1]=b[i]; sort(b+1,b+1+n); m=unique(b+1,b+1+n)-b-1; for(int i=1;i<=n;i++) a[i]=lower_bound(b+1,b+1+m,a[i])-b; for(int i=n;i>1;i--) { while(q.size()&&a[i]>q.top().first) { add(1,0,m,q.top().first,-1); vis[q.top().second]=0; q.pop(); } q.push({a[i],i}); vis[i]=1; add(1,0,m,q.top().first,1); if(a[i-1]>=a[i]) ans=ans+min(c[1],ask(1,0,m,a[i-1])+1); else ans=ans+1; } maxx=0; for(int i=n;i>=1;i--) { if(vis[i]) break; if(a[i]>=maxx) { ans++; maxx=a[i]; } } cout<<ans; }

i=1的答案显然是n,此后答案是单调不增的。 考虑什么时候答案会变小 既有一个炸弹放在了n后面时 例如n * 那么n-1能不能用呢 要查看n,n-1和炸弹的相对位置了 例如* n n-1 * 就可以用n-1 *****n * n-1 也可以 **n n-1 **就不可以 思考一下发现可以使用线段树,判断能不能用i时,把炸弹位置加一,大于i的位置减一,则需要所有包含pos[i]的区间都要区间和<=0。所以考虑维护以r为右端点的最小值,以l为左端点的最大值。需要判断的是以pos[i]为右端点的最小值和以pos[i]+1为左端点的最大值相加小于等于0 如果满足,i就可以当答案。否则需要继续减小。 int pos[300010]; int n,maxx[1200010],sum[1200010],minn[1200010]; void add(int x,int l,int r,int d,int v) { if(l==r) { sum[x]+=v; minn[x]+=v; maxx[x]+=v; return ; } int mid=(l+r)/2; if(d<=mid) add(x*2,l,mid,d,v); else add(x*2+1,mid+1,r,d,v); sum[x]=sum[x*2]+sum[x*2+1]; maxx[x]=max(maxx[x*2],sum[x*2]+maxx[x*2+1]); minn[x]=min(minn[x*2+1],sum[x*2+1]+minn[x*2]); } pair<int,int> askminn(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return {sum[x],minn[x]}; int mid=(l+r)/2; if(tr<=mid) return askminn(x*2,l,mid,tl,tr); if(tl>mid) return askminn(x*2+1,mid+1,r,tl,tr); pair<int,int>t1=askminn(x*2,l,mid,tl,tr); pair<int,int>t2=askminn(x*2+1,mid+1,r,tl,tr); return {t1.first+t2.first,min(t2.second,t2.first+t1.second)}; } pair<int,int> askmaxx(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return {sum[x],maxx[x]}; int mid=(l+r)/2; if(tr<=mid) return askmaxx(x*2,l,mid,tl,tr); if(tl>mid) return askmaxx(x*2+1,mid+1,r,tl,tr); pair<int,int>t1=askmaxx(x*2,l,mid,tl,tr); pair<int,int>t2=askmaxx(x*2+1,mid+1,r,tl,tr); return {t1.first+t2.first,max(t1.second,t1.first+t2.second)}; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) pos[read()]=i; int ans=n; for(int i=1;i<=n;i++) { while(askmaxx(1,1,n+1,pos[ans]+1,n+1).second+askminn(1,1,n+1,1,pos[ans]).second>0) { add(1,1,n+1,pos[ans],-1); ans--; } printf("%d ",ans); int x=read(); add(1,1,n+1,x,1); } }

一个方法是n^2地枚举所有段,计算mex。最后扫一下大伙,谁第一个没出现 然后我想到了从小到大枚举,看看x是否在mex里没有出现过。我们可以把所有的x看做隔档,看隔开后的小段是否凑齐了1到x-1 如果存在隔开后的小段mex为x,则该考虑x+1了。否则答案就是x了 可以发现我们把O(n^2)个子段变成了O(n)个子段。 求区间mex可以离线地使用莫队或者线段树。恰好可以发现得到O(n)个子段后,又变得可以离线了。 综上。我们用每个相邻的x做隔断,得到O(n)个子段。他们的mex即为全体子段的mex可能值。 然后离线地使用莫队求一下mex即可。 struct node { int l,r,v,b;//左端点,右端点,被谁分隔,所属于的块 friend bool operator<(node a,node b) { return a.b==b.b?a.r<b.r:a.b<b.b; } }o[300010]; int m,sum[300010],now=1,ans=3,n,a[300010],flag[300010]; vector<int>pos[300010]; void qu(int x) { sum[a[x]]--; if(sum[a[x]]==0) now=min(now,a[x]); } void ad(int x) { sum[a[x]]++; while(sum[now]) now++; } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) { a[i]=read(); pos[a[i]].push_back(i); } if(pos[1].size()==n)//只有1 { printf("1"); return 0; } else if(pos[1].size()==0)//没有1 { printf("2"); return 0; } int s=sqrt(n); for(int i=3;i<=n+1;i++) { if(pos[i].size()==0) { o[++m]={1,n,i,1}; break; } else { if(pos[i][0]!=1) o[++m]={1,pos[i][0]-1,i,1}; if(pos[i][pos[i].size()-1]!=n) o[++m]={pos[i][pos[i].size()-1]+1,n,i,pos[i][pos[i].size()-1]/s+1}; for(int j=0;j+1<pos[i].size();j++) { if(pos[i][j]+1!=pos[i][j+1]) o[++m]={pos[i][j]+1,pos[i][j+1]-1,i,pos[i][j]/s+1}; } } } int l=1,r=0; sort(o+1,o+1+m); for(int i=1;i<=m;i++) { while(r<o[i].r) { r++; ad(r); } while(r>o[i].r) { qu(r); r--; } while(l<o[i].l) { qu(l); l++; } while(l>o[i].l) { l--; ad(l); } if(now==o[i].v) flag[now]=1; } while(flag[ans]) ans++; cout<<ans; }

这题挺套路的 三维偏序 考虑第一维可以排个序,然后双指针一下 第二维可以用离散化一下,作为线段树的"下标" 第三位用线段树维护 总的来说,维护区间最大值。则对于i号人,只需要看大于i的i的那些人,有没有r大于i的r的即可。 int n,a[500010],m; int maxx[2000010],ans; struct node { int b,i,r; friend bool operator <(node a,node b) { return a.b>b.b;//从大到小地排序 } }o[500010]; void add(int x,int l,int r,int d,int v) { maxx[x]=max(maxx[x],v); if(l==r) return ; int mid=(l+r)/2; if(d<=mid) add(x*2,l,mid,d,v); else add(x*2+1,mid+1,r,d,v); } int ask(int x,int l,int r,int tl,int tr) { if(tl<=l&&r<=tr) return maxx[x]; int mid=(l+r)/2; if(tr<=mid) return ask(x*2,l,mid,tl,tr); if(tl>mid) return ask(x*2+1,mid+1,r,tl,tr); return max(ask(x*2,l,mid,tl,tr),ask(x*2+1,mid+1,r,tl,tr)); } int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) o[i].b=read(); for(int i=1;i<=n;i++) a[i]=o[i].i=read(); for(int i=1;i<=n;i++) o[i].r=read(); sort(o+1,o+1+n); sort(a+1,a+1+n); m=unique(a+1,a+1+n)-a-1; for(int i=1;i<=n;i++) o[i].i=lower_bound(a+1,a+1+m,o[i].i)-a; for(int i=1;i<=n;i++) { int j=i; while(j+1<=n&&o[j+1].b==o[j].b) j++; for(int k=i;k<=j;k++) if(ask(1,1,m+1,o[k].i+1,m+1)>o[k].r) ans++; for(int k=i;k<=j;k++) add(1,1,m+1,o[k].i,o[k].r); i=j; } cout<<ans; }

一眼折半搜索,但是具体实现不好实现,抄了洛谷题解 考虑枚举前一半的x,后一半的y 令bi=count(前一半ai^x),ci=count(后一半ai^x),则需要bi+ci=b1+c1 只需要用map存bi-b1 然后寻找c1-ci即可 int count(int x) { int sum=0; while(x) { sum++; x=x&(x-1); } return sum; } map<vector<int>,int>o; int n,a[110]; int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int x=(1<<15)-1;x>=0;x--) { int b1=count((a[1]>>15)^x); vector<int>t; for(int i=2;i<=n;i++) t.push_back(count((a[i]>>15)^x)-b1); o[t]=x; } for(int x=0;x<(1<<15);x++) { int c1=count( (a[1]-(a[1]>>15<<15))^x); vector<int>t; for(int i=2;i<=n;i++) t.push_back(c1-count( (a[i]-(a[i]>>15<<15))^x)); if(o.count(t)) { cout<<(o[t]<<15)+x; return 0; } } cout<<-1; }

考虑对于集合里的点,从点到"集合"连一条ai+bx的边。则为了不存在rainbow,需要新图里没有环,所以跑一跑最大生成树即可。 int n,m,a[100010],b[100010]; int fa[200010],tot; ll ans; struct edge { int x,y,v; friend bool operator<(edge a,edge b) { return a.v>b.v; } }e[200010]; int getfa(int x) { return fa[x]==x?x:fa[x]=getfa(fa[x]); } int main() { // freopen("1.in","r",stdin); m=read(); n=read(); for(int i=1;i<=m;i++) a[i]=read(); for(int i=1;i<=n;i++) b[i]=read(); for(int i=1;i<=m;i++) { for(int s=read();s;s--) { tot++; int x=read(); e[tot]={i+n,x,a[i]+b[x]}; ans+=a[i]+b[x]; } } for(int i=1;i<=n+m;i++) fa[i]=i; sort(e+1,e+1+tot); for(int i=1;i<=tot;i++) { if(getfa(e[i].x)==getfa(e[i].y)) continue; ans-=e[i].v; fa[fa[e[i].x]]=fa[e[i].y]; } cout<<ans; }

令siz表示某颜色的边的数量 则如果边的数量小于等于根号n,使用搜索找到“用这个颜色的边构成的联通块”。联通快的大小是O(siz)的。然后O(siz^2logn)地用map累加连通块内任意两点间的距离。这样最多做n/siz次,所以这种操作复杂度是O(n/siz*siz*siz*logn)=O(n根号nlogn) 如果边的数量大于根号n,那么可以暴力O(n)地跑并查集,然后对于每个询问用并查集问一问,累加答案。做一次复杂度是复杂度O((n+q)*小常数)。这样最多做O(n/siz)=O(根号n)次,所以总复杂度仍未O(n根号n*并查集的常数) int vis[100010],u[100010],v[100010],ans[100010],n,m,fa[100010]; struct edge { int x,y; }; vector<edge>e[100010]; vector<int>a,ee[100010]; unordered_map<int,int>f[100010]; int getfa(int x) { return fa[x]==x?x:fa[x]=getfa(fa[x]); } void dfs(int x) { vis[x]=1; a.push_back(x); for(auto y:ee[x]) { if(vis[y])continue; dfs(y); } } int main() { n=read(); m=read(); for(int i=1;i<=m;i++) { int x=read(),y=read(); e[read()].push_back({x,y}); } int q=read(); for(int i=1;i<=q;i++) u[i]=read(),v[i]=read(); for(int i=1;i<=m;i++) { if(e[i].size()<=316) { for(auto j:e[i]) { vis[j.x]=0; vis[j.y]=0; ee[j.x].clear(); ee[j.y].clear(); } for(auto j:e[i]) ee[j.x].push_back(j.y),ee[j.y].push_back(j.x); for(auto j:e[i]) if(vis[j.x]==0) { a.clear(); dfs(j.x); for(int x=0;x<a.size();x++) for(int y=x+1;y<a.size();y++) f[a[x]][a[y]]++; } } else { for(int j=1;j<=n;j++) fa[j]=j; for(auto j:e[i]) { if(getfa(j.x)==getfa(j.y)) continue; fa[fa[j.x]]=fa[j.y]; } for(int j=1;j<=q;j++) if(getfa(u[j])==getfa(v[j])) ans[j]++; } } for(int i=1;i<=q;i++) printf("%d\n",ans[i]+f[u[i]][v[i]]+f[v[i]][u[i]]); }

把玩一下样例,可以发现当所有长为k的子串,2^k种情况全都出现过,则输出no。 所以容易想到k很大的时候,2^k不能全部出现,输出yes即可 否则k比较小时,需要扫一下判断no。 因此k那么大没啥用,前几位贪心地选0,因为需求的是最小字典序。到了后20位时谨慎一点。 我们把前缀全为1的长为k的后缀放在set里,然后判断第i位是0还是1,只需扫一遍set 复杂度O(nlog^2) int n,k,vis[2000000],sum[1000010]; char s[1000010]; set<int>o,oo; void work() { n=read();k=read(); scanf("%s",s+1); if(k<=20&&(1<<k)<=(n-k+1))//只有k比较小,2^k都出现了才无解 { int sum=0; for(int i=0;i<(1<<k);i++) vis[i]=0; for(int i=1;i+k-1<=n;i++) { int t=0; for(int j=i;j<i+k;j++) t=t*2+s[j]-'0'; vis[t]=1; } for(int i=0;i<(1<<k);i++) sum+=vis[i]; if(sum==(1<<k)) { printf("NO\n"); return ; } } for(int i=1;i<=n;i++) sum[i]=sum[i-1]+(s[i]=='0'); printf("YES\n"); for(int i=1;i<=k-20;i++)//前几位大部分是0 printf("0"); int len=max(0,k-20),res=k-len;//前len位已确定后res位未确定 o.clear(); for(int i=len+1;i+res-1<=n;i++) { if(sum[i-1]-sum[i-len-1]) continue; int t=0; for(int j=i;j<=i+res-1;j++) t=t*2+s[j]-'0'; o.insert(t); } for(int i=res-1;i>=0;i--)//确定从右往左第i位 { int sum=0; for(auto x:o) { if(x&(1<<i)) sum++; } oo.clear(); if(sum==(1<<i)) { printf("1"); for(auto x:o) if((x&(1<<i))==0) oo.insert(x); } else { printf("0"); for(auto x:o) if((x&(1<<i))) oo.insert(x-(1<<i)); } swap(oo,o); } printf("\n"); } int main() { // freopen("1.in","r",stdin); // freopen("2.out","w",stdout); for(int q=read();q;q--) work(); }

首先D1是一个比较显然的动态规划。在此基础上,把这个f数组输出一下,发现第i行的分母可以变为2^(i-1),此时分母遵循一个类似组合数的f[i][j]=f[i-1][j]+f[i-1][j-1]。 ll mod=1e9+7; ll n,m,k,f[2010][2010]; void work() { n=read();m=read();k=read(); printf("%lld\n",f[n][n-m]*k%mod); } int main() { // freopen("1.in","r",stdin); for(int i=1;i<=2000;i++) for(int j=0;j<=2000;j++) if(j==0) f[i][j]=(f[i-1][j]+1)%mod; else f[i][j]=(f[i-1][j]+f[i-1][j-1])*500000004%mod; for(int q=read();q;q--) work(); } 找规律代码 int c(int m,int n) { int C=1; if (m>n-m) m=n-m; for (int i=1;i<=m;i++) C = (n-i+1) * C / i; return C; } ll mod=1e9+7; ll n,m,k,a[2010][2010],b[2010][2010]; int main() { // freopen("1.in","r",stdin); for(int i=1;i<=10;i++) { for(int j=0;j<=i;j++) { if(j==0) { b[i][j]=1<<(i-1); a[i][j]=b[i][j]*i; } else { a[i][j]=a[i-1][j]+a[i-1][j-1]; b[i][j]=b[i-1][j]*2; if(a[i][j]==0) b[i][j]=b[i][j-1]; } // cout<<a[i][j]<<'/'<<b[i][j]<<' '; printf("%4lld ",a[i][j]); } cout<<endl; } for(int i=1;i<=10;i++) { for(int j=0;j<=i;j++) { int sum=0; for(int ii=1;ii<=i-j;ii++) sum=sum+ii*pow(2,ii-1)*c(i-ii-j,i-ii-1); if(j==0) printf("%4d ",i*(int)pow(2,i-1)); else printf("%4d ",sum); } cout<<endl; } } 找到规律后考虑用组合数O(nlogn)地计算每一项即可。 #include<bits/stdc++.h> using namespace std; typedef long long ll; int read() { int x;scanf("%d",&x); return x; } ll mod=1e9+7,g[1000010],f[1000010]; ll c(ll n,ll m) { return f[m]*g[n]%mod*g[m-n]%mod; } ll quick(ll a,ll b) { ll t=1; while(b) { if(b&1) t=t*a%mod; a=a*a%mod; b=b/2; } return t; } ll n,m,k,ans; void work() { n=read();m=read();k=read(); m=n-m;ans=0; if(m==0) { printf("%lld\n",n*k%mod); return ; } for(int i=1;i<=n-m;i++) ans=(ans+i*quick(2,i-1)%mod*c(n-i-m,n-i-1)%mod)%mod; ans=ans*quick(quick(2,n-1),mod-2)%mod; printf("%lld\n",ans*k%mod); } int main() { // freopen("1.in","r",stdin); f[0]=1; for(int i=1;i<=1000000;i++) f[i]=f[i-1]*i%mod; g[1000000]=quick(f[1000000],mod-2); for(int i=999999;i>=0;i--) g[i]=g[i+1]*(i+1)%mod; for(int t=read();t;t--) work(); }

考虑对a排序,选择第一个,与23中的一个、45中的一个、67中的一个... 这样即可保证选择的n/2+1个里满足a的要求 然后相邻两个里选时,选择b较大的即可。 struct node { int a,b,i; friend bool operator <(node a,node b) { return a.a>b.a; } }o[100010]; int n; int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) o[i]={read(),0,i}; for(int i=1;i<=n;i++) o[i].b=read(); sort(o+1,o+1+n); cout<<n/2+1<<'\n'<<o[1].i<<' '; for(int i=2;i<=n;i+=2) { if(o[i].b<=o[i+1].b) cout<<o[i+1].i<<' '; else cout<<o[i].i<<' '; } }

对每个点连0 i a[i] 对每条边连i+n,n+m+1,z和x i+n inf,y i+n inf 最小割的定义是删边的最小花费使得s到t不连通 因为点到边的边权是inf 所以s到t不连通要么s到点不连通,要么边到t不连通了。 s到点不连通等价于不使用这个点,付出了ai的代价 边到t不连通等价于不用这条边,也付出z的代价 所以用Σz减去付出的代价即可。 struct edge { int y; ll dis; int next; }e[20010]; int head[2010],tot,d[2010],m,n,used[2010]; ll ans; void add(int x,int y,int v) { tot++; e[tot]={y,v,head[x]}; head[x]=tot; tot++; e[tot]={x,0,head[y]}; head[y]=tot; } bool bfs() { int x; queue<int>q; q.push(0); memset(d,0,sizeof(d)); d[0]=1; while(q.size()) { x=q.front(); q.pop(); for(int i=head[x];i;i=e[i].next) { if(e[i].dis!=0&&d[e[i].y]==0) { d[e[i].y]=d[x]+1; q.push(e[i].y); } } } return d[n+m+1]!=0; } ll dfs(ll x,ll in) { ll out=0,i,k; if(x==n+m+1) return in; for(i=used[x];i&&in!=0;i=e[i].next,used[x]=i) { if(e[i].dis!=0&&d[e[i].y]==d[x]+1) { k=dfs(e[i].y,min(e[i].dis,in)); e[i].dis-=k; e[i^1].dis+=k; in-=k; out+=k; } } if(out==0) d[x]=0; return out; } int main() { // freopen("1.in","r",stdin); tot=1; n=read();m=read(); for(int i=1;i<=n;i++) add(0,i,read()); for(int i=1;i<=m;i++) { int x=read(),y=read(),z=read(); add(i+n,n+m+1,z); add(x,i+n,1e9); add(y,i+n,1e9); ans+=z; } while(bfs()) { memcpy(used,head,sizeof(head)); ans-=dfs(0,1e18); } cout<<ans; }

我首先绞尽脑汁写了一个dp c[i]是b[i]的前缀和。 f[i]表示第i位置是最后一次使用b[i]=a[i]的位置 则答案是Σf[i],转移时本来f[i]=Σf[j],但是如果存在b[j]-c[j]==b[i]-c[i],则可以将f[j]清空 f[0]=1; for(int i=1;i<=n;i++) { f[i]=0; for(int j=0;j<i;j++) { f[i]+=f[j]; if(b[j]-c[j]==b[i]-c[i]) f[j]=0; } } for(int i=0;i<=n;i++) { cout<<f[i]<<' '; ans+=f[i]; } cout<<endl; cout<<ans<<endl; 在这个基础上加一点优化和取模即可 ll mod=1e9+7; ll n,c[200010],b[200010],sum; map<ll,ll>o; void work() { n=read(); for(int i=1;i<=n;i++) { b[i]=read(); c[i]=c[i-1]+b[i]; } o.clear(); sum=1; o[0]=1; for(int i=1;i<=n;i++) { if(o[b[i]-c[i]]) { ll t=sum; sum=((sum+sum-o[b[i]-c[i]])%mod+mod)%mod; o[b[i]-c[i]]=t; } else { o[b[i]-c[i]]=sum; sum=sum*2%mod; } } cout<<(sum+mod)%mod<<'\n'; } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

考虑线段树 为了不让区间出现abc,mid到mid+1左右两边总要进行分工的 要么左边没有a,此时压力落在了右边,右边不能有abc 要么左边没有abc,此时右边不能有c 要么左边没有ab,右边没有bc 你要问左边没有b,右边没有b不是也行 那我只能说你dp学得不深 a[x]=a[x*2]+a[x*2+1]; b[x]=b[x*2]+b[x*2+1]; c[x]=c[x*2]+c[x*2+1]; ab[x]=min(ab[x*2]+b[x*2+1],a[x*2]+ab[x*2+1]); bc[x]=min(bc[x*2]+c[x*2+1],b[x*2]+bc[x*2+1]); int n,q,a[400010],b[400010],c[400010],ab[400010],bc[400010],abc[400010]; char s[100010]; int minnn(int x,int y,int z) { x=min(x,y); return min(x,z); } void pushup(int x) { a[x]=a[x*2]+a[x*2+1]; b[x]=b[x*2]+b[x*2+1]; c[x]=c[x*2]+c[x*2+1]; ab[x]=min(ab[x*2]+b[x*2+1],a[x*2]+ab[x*2+1]); bc[x]=min(bc[x*2]+c[x*2+1],b[x*2]+bc[x*2+1]); abc[x]=minnn(a[x*2]+abc[x*2+1],ab[x*2]+bc[x*2+1],abc[x*2]+c[x*2+1]); } void build(int x,int l,int r) { if(l==r) { if(s[l]=='a') a[x]=1; if(s[l]=='b') b[x]=1; if(s[l]=='c') c[x]=1; return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); pushup(x); } void add(int x,int l,int r,int d) { if(l==r) { a[x]=b[x]=c[x]=0; if(s[l]=='a') a[x]=1; if(s[l]=='b') b[x]=1; if(s[l]=='c') c[x]=1; return ; } int mid=(l+r)/2; if(d<=mid) add(x*2,l,mid,d); else add(x*2+1,mid+1,r,d); pushup(x); } int main() { // freopen("1.in","r",stdin); n=read();q=read(); scanf("%s",s+1); build(1,1,n); for(;q;q--) { int x=read(); scanf(" %c",&s[x]); add(1,1,n,x); printf("%d\n",abc[1]); } }

线性基 考虑离线地做,对询问排序 那么当有了i个数字时,问能不能拼出来x 维护一个数组表示能拼出来的数字,sum表示用了几个数字 那么新来一个数字,如果原来拼不出来,就要加进线性基里,然后重新跑f数组 求答案时,如果拼不出来显然是0,否则答案是2^(i-sum)。因为线性基以外的数字任意取或者不取,方案数是这么多。每种取得方案,用线性基这sum个数字有且仅有一组方案使得异或和恰好为x int n,q,f[23][2000000],sum,a[100010]; ll ans=1,mod=1e9+7; struct node { int i,x,ans,pos; friend bool operator <(node a,node b) { return a.i<b.i; } }o[100010]; bool pos_(node a,node b) { return a.pos<b.pos; } int main() { // freopen("1.in","r",stdin); f[0][0]=1; n=read();q=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int i=1;i<=q;i++) { o[i].i=read(); o[i].x=read(); o[i].pos=i; } sort(o+1,o+1+q); ans=1; for(int i=1;i<=q;i++) { for(int j=o[i-1].i+1;j<=o[i].i;j++) { if(f[sum&1][a[j]]){ ans=ans*2%mod; continue; } for(int y=0;y<(1<<20);y++) { if(f[sum&1][y]) f[(sum&1)^1][y]=f[(sum&1)^1][y^a[j]]=1; } sum++; } if(f[sum&1][o[i].x]) o[i].ans=ans; } sort(o+1,o+1+q,pos_); for(int i=1;i<=q;i++) printf("%d\n",o[i].ans); }

众所周知,欧拉函数是积性函数。若 n = p^k,其中 p 是质数,那么 phi(n) = p^k - p^(k - 1)。 所以对每个质数分别计算贡献,复杂度62qlogn。理论存在,开始卡常! 维护区间乘积是p的几次方,则区间乘p^k等价于区间加k,询问是区间求和。 首先把线段树变成了树状数组,后来树状数组常数又优化了一点点,最后发现:维护k的几次方时,不需要对mod-1取模,因为最坏情况下是ai=256且进行了 q-1次1到n区间乘256,此时最大也就qnlog(300),long long存得下。最后扔掉了对mod-1取模就过了 快读快写什么的都整上了哈哈哈哈 typedef long long ll; char buf[1<<15],*fs,*ft; inline char getc(){ return (fs==ft&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),fs==ft))?0:* fs++; } inline int read(){ int This=0,F=1; char ch=getc(); while(ch<'0'||ch>'9'){ if(ch=='-') F=-1; ch=getc(); } while(ch>='0'&&ch<='9'){ This=(This<<1)+(This<<3)+ch-'0'; ch=getc(); } return This*F; } inline void write(int x) { if(x==0) { putchar('0'); return; } int num=0;char ch[16]; while(x) ch[++num]=x%10+'0',x/=10; while(num) putchar(ch[num--]); putchar('\n'); } ll mod=1e9+6,mod1=1e9+7; ll n,C[400010],D[400010]; ll quick(ll a,ll b) { if(b==-1) return 0; ll t=1; while(b) { if(b&1) t=t*a%mod1; a=a*a%mod1; b=b/2; } return t; } pair<ll,ll> sum(int i) { pair<ll,ll> res={0,0}; while(i>0) { res.first+=C[i]; res.second+=D[i]; i-=i&-i; } return res; } void update(int i,ll v1,ll v2) { while(i<=n+1) { C[i]+=v1; D[i]+=v2; i+=i&-i; } } ll ask(int tl,int tr) { pair<ll,ll>a,b; a=sum(tr+1); b=sum(tl-1); return a.first*(tr+1)-a.second-1ll*b.first*tl+b.second; } void add(int tl,int tr,int v) { update(tl,v,v*tl); update(tr+1,-v,-v*(tr+1)); } int q,num[400010],l[400010],r[400010],v[400010],a[400010]; char s[400010]; ll ans[400010],t[400010]; vector<int>pri; int main() { for(int i=2;i<=300;i++) { int flag=1; for(int j=2;j<i;j++) if(i%j==0) flag=0; if(flag==1) pri.push_back(i); } n=read();q=read(); for(int i=1;i<=n;i++) num[i]=read(); for(int i=1;i<=q;i++) { s[i]=getc(); if(s[i]=='T') for(int j=1;j<=6;j++) getc(); else for(int j=1;j<=7;j++) getc(); if(s[i]=='T') l[i]=read(),r[i]=read(); else l[i]=read(),r[i]=read(),v[i]=read(); ans[i]=1; } for(auto x:pri) { for(int i=1;i<=n+1;i++) C[i]=D[i]=0; int sum=0; for(int i=1;i<=n;i++) { a[i]=0; while(num[i]%x==0) { num[i]=num[i]/x; a[i]++; sum++; } if(a[i]) add(i,i,a[i]); } for(int i=1;i<=q;i++) { if(s[i]=='M') { t[i]=0; while(v[i]%x==0) { t[i]++; sum++; v[i]=v[i]/x; } } } if(sum==0) continue; for(int i=1;i<=q;i++) { if(s[i]=='T') { t[i]=ask(l[i],r[i]); if(t[i]) ans[i]=ans[i]*quick(x,t[i]-1)%mod1*(x-1)%mod1; } else if(t[i]) add(l[i],r[i],t[i]); } } for(int i=1;i<=q;i++) if(s[i]=='T') write(ans[i]); }

额啊,还以为每个点有自己的值,原来是每个数字只出现一次 所以sb题 考虑给每个点加一 令ans[i]表示至少包含1到i的,那么容斥一下,仅包含1到i的方案数=包含1到i+1的-包含1到i的 考虑包含1到i-1的链左右端点是lr,那么i有几种情况: 1、i是l的子节点且必须和r的lca为1 2、i是r的子节点且必须和l的lca为1 以上的反例是1 2 ,2 3 ,42。原来的链是1 3 ,4来了之后可以发现没有包含1到4的链 3、i是l的父亲或者i是r的父亲,此时不需要更改 4、类似反例,i位于l到r路径上某个点的另一个子树里,此时可以break 如果普通情况,lr没有1的话,方案数显然是siz[l]*siz[r] 如果存在1的话,假设l是1,另一边仍然是siz[r],1这边是n-l的祖先的siz mex=0的话,答案是n*(n-1)/2-包含0的方案数。包含0的方案数扫一遍根节点的出边即可。 int n,siz[200010],d[200010],fa[200010][22]; ll ans[200010]; vector<int>e[200010]; void dfs(int x) { siz[x]=1; for(auto y:e[x]) { if(fa[x][0]==y)continue; fa[y][0]=x; d[y]=d[x]+1; dfs(y); siz[x]+=siz[y]; } } int lca(int x,int y) { if(d[x]>d[y]) swap(x,y); for(int i=20;i>=0;i--) { if(d[fa[y][i]]>=d[x]) y=fa[y][i]; } if(x==y) return x; for(int i=20;i>=0;i--) { if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i]; } return fa[x][0]; } void work() { n=read(); for(int i=1;i<=n+1;i++) { siz[i]=0; fa[i][0]=0; e[i].clear(); d[i]=0; ans[i]=0; } for(int i=1;i<n;i++) { int x=read()+1,y=read()+1; e[x].push_back(y); e[y].push_back(x); } d[1]=1; dfs(1); for(int i=1;i<=20;i++) for(int x=1;x<=n;x++) fa[x][i]=fa[fa[x][i-1]][i-1]; ll sum=1; for(auto y:e[1]) { ans[1]+=siz[y]*sum; sum+=siz[y]; } int l=1;int r=1; int il,ir,sl=-1,sr=-1; for(int i=2;i<=n;i++) { il=lca(i,l),ir=lca(i,r); if(il==l&&ir==1) { if(l==1) { sl=siz[i]; for(int j=i;fa[j][0]!=1;j=fa[j][0],sl=siz[j]); } l=i; } else if(ir==r&&il==1) { if(r==1) { sr=siz[i]; for(int j=i;fa[j][0]!=1;j=fa[j][0],sr=siz[j]); } r=i; } else if(ir!=i&&il!=i) break; if(l==1) ans[i]=1ll*siz[r]*(n-sr); else if(r==1) ans[i]=1ll*siz[l]*(n-sl); else ans[i]=1ll*siz[l]*siz[r]; } cout<<n*(n-1ll)/2-ans[1]<<' '; for(int i=2;i<=n+1;i++) cout<<ans[i-1]-ans[i]<<' '; cout<<'\n'; } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

写了个不知道叫啥的线段树 主旨是先扫一遍所有询问,把每个颜色以后最多能加多少sum[i],给算出来 接下来每次增加时,我先把这个sum全给你。在颜色增加时,就相当于未来能增加的变少了,sum减一下。 询问或者换颜色时,给还没加上的全部夺走,就相当于没加上嘛,于是只加上了这段时间内的 struct node { char s[6]; int l,r,c,x,i; }o[4000010]; int c[4000010],n,q,flag[4000010]; ll a[4000010],sum[4000010],lazy[4000010]; void build(int x,int l,int r) { c[x]=1; if(l==r){ a[l]=sum[1]; return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); } void pushdown(int x) { lazy[x*2]=lazy[x*2]+lazy[x]; lazy[x*2+1]=lazy[x*2+1]+lazy[x]; lazy[x]=0; c[x*2]=c[x]; c[x*2+1]=c[x]; flag[x*2]=1; flag[x*2+1]=1; flag[x]=0; } void add(int x,int l,int r,int tl,int tr,int col) { if(tl<=l&&r<=tr&&c[x]) { lazy[x]=lazy[x]-sum[c[x]]+sum[col]; c[x]=col; flag[x]=1; return ; } if(flag[x]) pushdown(x); int mid=(l+r)/2; if(tl<=mid) add(x*2,l,mid,tl,tr,col); if(tr>mid) add(x*2+1,mid+1,r,tl,tr,col); if(c[x*2]==c[x*2+1]) c[x]=c[x*2]; else c[x]=0; } int work(int x,int l,int r,int d) { if(l==r){ a[l]+=lazy[x]; lazy[x]=0; return c[x]; } if(flag[x]) pushdown(x); int mid=(l+r)/2; if(d<=mid) return work(x*2,l,mid,d); else return work(x*2+1,mid+1,r,d); } int main() { // freopen("1.in","r",stdin); n=read();q=read(); for(int i=1;i<=q;i++) { scanf("%s",o[i].s); if(o[i].s[0]=='C') { o[i].l=read(); o[i].r=read(); o[i].c=read(); } if(o[i].s[0]=='A') { o[i].c=read(); o[i].x=read(); sum[o[i].c]+=o[i].x; } else o[i].i=read(); } build(1,1,n); for(int i=1;i<=q;i++) { if(o[i].s[0]=='C') add(1,1,n,o[i].l,o[i].r,o[i].c); else if(o[i].s[0]=='A') sum[o[i].c]-=o[i].x; else { int color=work(1,1,n,o[i].i); cout<<a[o[i].i]-sum[color]<<'\n'; } } }

考虑如果x不等于y,则从x向y连边,表示x如果选了人,y就不能选猫,也必须选人 则从1跑一遍有向图强连通分量。如果发现sum[cnt]==n,则证明所有点处于一个强联通分量里,则不存在合法方案,输出no 否则,考虑缩点后的有向无环图,把没有出边的那个强联通分量取人,其他强联通分量取猫即可 可以发现只从1跑一下tarjan即可 int dfn[1000010],low[1000010]; int num,c[1000010],ins[1000010],n,m,cnt,sum[1000010]; vector<int>e[1000010]; stack<int>q; void tarjan(int x) { dfn[x]=low[x]=++num; q.push(x); ins[x]=1; for(auto y:e[x]) { if(!dfn[y]) { tarjan(y); low[x]=min(low[x],low[y]); } else if(ins[y]) { low[x]=min(low[x],low[y]); } } if(dfn[x]==low[x]) { cnt++; int y; do{ y=q.top(); q.pop(); ins[y]=0; c[y]=cnt; sum[cnt]++; }while(x!=y); } } void work() { n=read();m=read(); for(int i=1;i<=n;i++) { dfn[i]=low[i]=0; c[i]=0; sum[i]=0; e[i].clear(); } num=0; cnt=0; for(int i=1;i<=m;i++) { int x=read();int y=read(); if(x!=y) e[x].push_back(y); } tarjan(1); if(sum[cnt]==n) printf("No\n"); else { printf("Yes\n"); cout<<sum[1]<<' '<<n-sum[1]<<'\n'; for(int i=1;i<=n;i++) if(c[i]==1) cout<<i<<' '; cout<<'\n'; for(int i=1;i<=n;i++) if(c[i]!=1) cout<<i<<' '; cout<<'\n'; } } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

stl大师 首先理解题意。题目不允许把一个单词中的一段替换成另一个单词,只允许整个单词整个地替换。所以显然是一个最短路问题 先把单词读进来,然后反向建边,跑多源最短路,维护每个点最少几个r,保证r数量最少的同时,最少长为几。最后扫一遍原来的n个单词。如果在图里出现过,那就拿着d更新答案。否则只能不动,拿着他自己更新答案。 记得第二维开ll pair<int,ll>ask(string s) { pair<int,ll>t={0,s.size()}; for(auto x:s) if(x=='r') t.first++; return t; } void work(string &s) { for(auto &x:s) if('A'<=x&&x<='Z') x=x-'A'+'a'; } int n,cnt,m,vis[100010]; priority_queue<pair<pair<int,ll>,int>,vector<pair<pair<int,ll>,int>>,greater<pair<pair<int,ll>,int>>>q; pair<int,ll>d[100010]; map<string,int>o; string a[100010],s[100010]; vector<int>e[100010]; int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++){ cin>>a[i]; work(a[i]); } m=read(); for(int i=1;i<=m;i++) { string x,y; cin>>x>>y; work(x); work(y); if(o[x]==0) { cnt++; o[x]=cnt; s[cnt]=x; } if(o[y]==0) { cnt++; o[y]=cnt; s[cnt]=y; } e[o[y]].push_back(o[x]); } for(int i=1;i<=cnt;i++) { d[i]=ask(s[i]); q.push({d[i],i}); } while(q.size()) { int x=q.top().second; q.pop(); if(vis[x]) continue; vis[x]=1; for(auto y:e[x]) { if(d[x]<d[y]) { d[y]=d[x]; q.push({d[x],y}); } } } pair<int,ll>ans={0,0},t; for(int i=1;i<=n;i++) { if(o[a[i]]) t=d[o[a[i]]]; else t=ask(a[i]); ans.first+=t.first; ans.second+=t.second; } cout<<ans.first<<' '<<ans.second; }

挺简单的,为啥2400 考虑受到伤害当且仅当大于等于b的点的数量大于等于a 如果小于a,显然输出0 否则我们对大于等于b的怪物算一下概率为(cnt-a)/cnt 对于小于b的怪物算一下概率为(cnt+1-a)/(cnt+1) 前缀和一下子即可 ll mod=998244353; ll quick(ll a,ll b) { ll t=1; while(b) { if(b&1) t=t*a%mod; a=a*a%mod; b=b/2; } return t; } ll n,m,d[200010],sum[200010],f[200010],ans; int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) d[i]=read(); sort(d+1,d+1+n); for(int i=1;i<=n;i++) sum[i]=(sum[i-1]+d[i])%mod; for(int i=1;i<=n+1;i++) f[i]=quick(i,mod-2); for(;m;m--) { ll a=read();ll b=read(); int cnt=lower_bound(d+1,d+1+n,b)-d-1; cnt=n-cnt; if(cnt<a) cout<<"0\n"; else { ans=((sum[n]-sum[n-cnt])%mod+mod)%mod*(cnt-a)%mod*f[cnt]%mod; ans=ans+sum[n-cnt]*(cnt+1-a)%mod*f[cnt+1]%mod; cout<<ans%mod<<'\n'; } } }

首先他有来有回,并非有向无环图,所以不能拓扑排序地做,我们需要高斯消元。 但是复杂度接受不了。把每一行分开来做,然后内部是一个 2 -1 0 0 0 0 -1 3 -1 0 0 0 0 -1 3 -1 0 0 0 0 -1 3 -1 0 0 0 0 -1 3 -1 0 0 0 0 -1 2 的矩阵,可以发现是一个稀疏矩阵,从上往下再从下往上扫一扫即可。 找规律代码: double a[1010][1010],f[1010]; int n,m,x,y; int main() { freopen("1.in","r",stdin); n=read();m=read();x=read();y=read(); if(m==1) { printf("%.6lf",2.0*(n-1)); return 0; } // for(int t=1;t<n;t++)//做n-1次 { for(int i=2;i<n;i++) { a[i][i-1]=a[i][i+1]=-1; a[i][i]=3; } a[1][1]=2; a[1][2]=-1; a[n][n]=2; a[n][n-1]=-1; for(int i=1;i<=n;i++) { for(int j=1;j<=n;j++) cout<<a[i][j]<<' '; cout<<endl; } cout<<endl; // for(int i=1;i<=1;i++) // { for(int i=1;i<n;i++) { for(int j=n;j>=i;j--) a[i][j]/=a[i][i]; for(int j=n;j>=i;j--) a[i+1][j]-=a[i][j]*(a[i][i]/a[i+1][i]); } for(int x=1;x<=n;x++) { for(int y=1;y<=n;y++) cout<<a[x][y]<<' '; cout<<endl; } cout<<endl; a[n][n]/=a[n][n]; for(int i=n;i>1;i--) a[i-1][i]-=a[i-1][i]; for(int x=1;x<=n;x++) { for(int y=1;y<=n;y++) cout<<a[x][y]<<' '; cout<<endl; } } } 正解 double a[1010][1010],f[1010],b[1010]; int n,m,x,y; int main() { // freopen("1.in","r",stdin); n=read();m=read();x=read();y=read(); if(m==1) { printf("%.6lf",2.0*(n-x)); return 0; } n=n-(x-1); for(int t=1;t<n;t++)//做n-1次 { for(int i=2;i<m;i++) { a[i][i-1]=a[i][i+1]=-1; a[i][i]=3; b[i]=4+f[i]; } a[1][1]=2; a[1][2]=-1; b[1]=3+f[1]; a[m][m]=2; a[m][m-1]=-1; b[m]=3+f[m]; for(int i=1;i<m;i++) { b[i]/=a[i][i]; for(int j=i+1;j>=i;j--) a[i][j]/=a[i][i]; b[i+1]-=b[i]*(a[i][i]/a[i+1][i]); for(int j=i+1;j>=i;j--) a[i+1][j]-=a[i][j]*(a[i][i]/a[i+1][i]); } b[m]/=a[m][m]; a[m][m]/=a[m][m]; for(int i=m;i>1;i--) { b[i-1]-=b[i]*a[i-1][i]; a[i-1][i]-=a[i-1][i]; } for(int i=1;i<=m;i++) f[i]=b[i]; } printf("%.6lf",f[y]); }

看到n/3<k<k*2/3,鸽巢定理告诉我们,询问i,i+1,i+2三三一组,一定存在一个1和一个0。 不妨设b[1],b[2],b[3]是0,b[4].b[5],b[6]是1,那么从123过渡到456,总有一次是从0变到1的,那一次就可以确定前面的是0,后面的是1。 于是再询问一下b[2],b[3],b[4]、b[3],b[4],b[5],例如b[2],b[3],b[4]是1,则证明b[1]是0,b[4]是1 有了一个0位置和一个1位置,考虑对每个三三一组再使用两次询问确定答案。 如果0位置或1位置属于当前三三一组,则使用0+1+未知的方式得到未知数的值。 如果不属于,我们可以利用上之前询问的结果。 如果这三个0居多,那么询问前两个+1:如果得到1证明这两个里一定一个1一个0,第三个一定是0。只需要询问第一个+1+0,即可确定第一个和第二个;如果得到0证明这两个一定两个0,只需要询问第三个+1+0确定第三个即可。 如果这三个1居多,反过来做如上操作。 #include<bits/stdc++.h> using namespace std; int read() { int x;scanf("%d",&x);return x; } int ask(int x,int y,int z) { cout<<"? "<<x<<' '<<y<<' '<<z<<endl; return read(); } int sum,n,ans[10010],b[10],pos[2],a[10010]; void work() { n=read(); for(int i=1;i<=n;i++) ans[i]=-1; for(int i=1;i<=n;i+=3) a[i]=ask(i,i+1,i+2); for(int i=1;i<=n;i+=3) { if(a[i]==0&&a[i+3]==1) { b[1]=i; b[2]=i+1; b[3]=i+2; b[4]=i+3; b[5]=i+4; b[6]=i+5; break; } if(a[i]==1&&a[i+3]==0) { b[1]=i+5; b[2]=i+4; b[3]=i+3; b[4]=i+2; b[5]=i+1; b[6]=i; break; } } if(ask(b[2],b[3],b[4])==1){ pos[0]=b[1]; pos[1]=b[4]; } else if(ask(b[3],b[4],b[5])==1){ pos[0]=b[2]; pos[1]=b[5]; } else{ pos[0]=b[3]; pos[1]=b[6]; } ans[pos[0]]=0; ans[pos[1]]=1; for(int i=1;i<=n;i+=3) { if(i==pos[0]||i==pos[1]||i+1==pos[0]||i+1==pos[1]||i+2==pos[0]||i+2==pos[1]) { for(int j=i;j<i+3;j++) if(ans[j]==-1) ans[j]=ask(j,pos[0],pos[1]); continue; } if(a[i]==0) { if(ask(pos[1],i,i+1)==1)//i和i+1存在一个1,则i+2一定为0 { ans[i+2]=0; ans[i]=ask(pos[1],pos[0],i);//询问i是1还是0 ans[i+1]=1-ans[i]; } else//两个都为0 { ans[i]=ans[i+1]=0; ans[i+2]=ask(pos[1],pos[0],i+2);//询问i+1 } } else { if(ask(pos[0],i,i+1)==0)//i和i+1存在一个0 { ans[i+2]=1; ans[i]=ask(pos[1],pos[0],i); ans[i+1]=1-ans[i]; } else { ans[i]=ans[i+1]=1; ans[i+2]=ask(pos[1],pos[0],i+2); } } } sum=0; for(int i=1;i<=n;i++) if(ans[i]==0) sum++; cout<<"! "<<sum<<' '; for(int i=1;i<=n;i++) if(ans[i]==0) cout<<i<<' '; cout<<endl; } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

考虑动态规划,f[i]表示以i作为递增的结尾,此时的递减的结尾最大是多少 则如果a[i]>a[i-1],f[i]可以继承f[i-1] 否则如果a[i]>g[i-1],可以让a[i-1]做递减的结尾,我做递增的结尾,此时f[i]=a[i-1] 对两者取max,这样贪心地让后续能走得更远。 输出方案数则需要dp时记录答案,回溯回去。 g的动态规划与之类似 int f[200010],g[200010],a[200010],ans[200010],pref[200010],preg[200010]; int n; int main() { // f[i]表示以i为递增的结尾,递减的结尾最大是多少 f[1]=3e5; g[1]=-1; n=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int i=2;i<=n;i++) { f[i]=-1; g[i]=3e5; if(a[i]>a[i-1]){ f[i]=f[i-1]; pref[i]=0; } if(a[i]>g[i-1]&&a[i-1]>=f[i]){ f[i]=a[i-1]; pref[i]=1; } if(a[i]<a[i-1]){ g[i]=g[i-1]; preg[i]=1; } if(a[i]<f[i-1]&&a[i-1]<=g[i]){ g[i]=a[i-1]; preg[i]=0; } } if(f[n]==-1&&g[n]==300000) { cout<<"No"; return 0; } cout<<"Yes\n"; int pos=n,now; if(f[n]!=-1) now=0; else now=1; ans[n]=now; for(;pos!=0;pos--) { ans[pos]=now; if(now==1) now=preg[pos]; else now=pref[pos]; } for(int i=1;i<=n;i++) cout<<ans[i]<<' '; }

考虑存在长为奇数的回文路径时只需要存在xy有边且yx有边 长为偶数的回文路径只需要xy有边且yx有边且两条边的边权相同 于是使用map整一整即可 int n,m; map< pair<int,int>,int >sum; int cnt[2]; int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=m;i++) { char c; cin>>c; if(c=='+') { int x=read(),y=read(); cin>>c; if(sum[{y,x}]) cnt[1]++; if(sum[{y,x}]==c) cnt[0]++; sum[{x,y}]=c; } else if(c=='-') { int x=read(),y=read(); if(sum[{y,x}]==sum[{x,y}]) cnt[0]--; if(sum[{y,x}]) cnt[1]--; sum[{x,y}]=0; } else if(c=='?') { if(cnt[read()&1]) cout<<"YES\n"; else cout<<"NO\n"; } } }

考虑如果枚举an给b1分多少。如果分得多了,可能最后循环回来时,n的不够用。如果分得少了,可能中间a1到a[n-1]不够用。这两种情况都是非法情况,但是可以用不同返回值进行区分。 int n; int a[1000010],b[1000010]; int ask(int v)//如果an给b1分的是v { int now=v; for(int i=1;i<n;i++) { if(now+b[i]<a[i]) return 1; now=b[i]-max(0,a[i]-now); } if(now+b[n]-v>=a[n]) return 0; return -1; } void work() { n=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int i=1;i<=n;i++) b[i]=read(); int l=0,r=min(b[n],a[1]),mid; while(l+1<r) { mid=(l+r)/2; switch (ask(mid)) { case -1:r=mid;break; case 0:cout<<"YES\n"; return ; case 1:l=mid; } } if(ask(l)==0||ask(r)==0) cout<<"YES\n"; else cout<<"NO\n"; } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

考虑枚举ai是左边某一段的最大值,右边存在令一段可以断开的地方时,将中间断开,会对答案贡献-- 所以对于ai找到1到i-1里面最靠右的大于v的下标A,i+1到n的最靠左的大于v的下标C,C的右边的最靠左的小于v的下标D,则对答案的贡献减去(i-A+1)*(D-C) int n,a[300010]; ll ans; int maxx[1200010],minn[1200010]; void build(int x,int l,int r) { if(l==r) { maxx[x]=a[l];minn[x]=a[l]; return ; } int mid=(l+r)/2; build(x*2,l,mid); build(x*2+1,mid+1,r); maxx[x]=max(maxx[x*2],maxx[x*2+1]); minn[x]=min(minn[x*2],minn[x*2+1]); } int ask1(int x,int l,int r,int tl,int tr,int v)//区间最右的大于v的下标 { if(tr==0) return 0; if(l==r){ if(maxx[x]>v) return l; return 0; } int mid=(l+r)/2; if(tl<=l&&r<=tr) { if(maxx[x]<=v) return 0; int t=ask1(x*2+1,mid+1,r,tl,tr,v); if(t) return t; return ask1(x*2,l,mid,tl,tr,v); } if(tr>mid) { int t=ask1(x*2+1,mid+1,r,tl,tr,v); if(t) return t; } if(tl<=mid) return ask1(x*2,l,mid,tl,tr,v); return 0; } int ask2(int x,int l,int r,int tl,int tr,int v)//区间最左的大于v的下标 { if(tl==n+1) return n+1; if(l==r) { if(maxx[x]>v) return l; return n+1; } int mid=(l+r)/2; if(tl<=l&&r<=tr){ if(maxx[x]<=v) return n+1; int t=ask2(x*2,l,mid,tl,tr,v); if(t!=n+1) return t; return ask2(x*2+1,mid+1,r,tl,tr,v); } if(tl<=mid) { int t=ask2(x*2,l,mid,tl,tr,v); if(t!=n+1) return t; } if(tr>mid) return ask2(x*2+1,mid+1,r,tl,tr,v); return n+1; } int ask3(int x,int l,int r,int tl,int tr,int v)//区间最左的小于v的下标 { if(tl==n+1) return n+1; if(l==r) { if(minn[x]<v) return l; return n+1; } int mid=(l+r)/2; if(tl<=l&&r<=tr){ if(minn[x]>=v) return n+1; int t=ask3(x*2,l,mid,tl,tr,v); if(t!=n+1) return t; return ask3(x*2+1,mid+1,r,tl,tr,v); } if(tl<=mid) { int t=ask3(x*2,l,mid,tl,tr,v); if(t!=n+1) return t; } if(tr>mid) return ask3(x*2+1,mid+1,r,tl,tr,v); return n+1; } void work() { n=read(); for(int i=1;i<=n;i++) a[i]=read(); ans=0; build(1,1,n); for(int i=1;i<=n;i++) { ans=ans+1ll*(1+n-i)*(n-i)/2; ll A=ask1(1,1,n,1,i-1,a[i])+1; int C=ask2(1,1,n,i+1,n,a[i]); int D; if(C==n+1) D=n+1; else D=ask3(1,1,n,C,n,a[i]); ans=ans-(i-A+1)*(D-C); } cout<<ans<<'\n'; } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

将所有情况枚举一下,发现看做012的同余系的话,对于每一个相邻的两行,a[i][j+1]-a[i][j]是相同的。对于每一列也同理。 因此维护f[i]其中i=1到n表示每相邻行之间的数字的差值,f[i]其中i=n+1到n+m表示相邻列之间的数字的差值。 可以发现,由于相邻的数字值不同,f[i]的取值只有1和2 则如果y1+1==y2,证明f[x2]和f[y2+n]需要不同 如果y2+1==y1,证明f[x2]和f[y1+n]需要相同 建图跑染色即可。 int n,m,f[4010]; vector<int>e[4010],ee[4010]; int dfs(int x) { for(auto y:e[x]) { if(f[y]==-1) { f[y]=3-f[x]; if(dfs(y)) return 1; } else if(f[x]==f[y]) return 1; } for(auto y:ee[x]) { if(f[y]==-1) { f[y]=f[x]; if(dfs(y)) return 1; } else if(f[y]+f[x]==3) return 1; } return 0; } void work() { n=read();m=read(); for(int i=1;i<=n+m+2;i++) { f[i]=-1; e[i].clear(); ee[i].clear(); } for(int k=read();k;k--) { int x1,x2,y1,y2; x1=read();y1=read();x2=read();y2=read(); if(y1+1==y2) { e[x2].push_back(y2+n);//不同 e[y2+n].push_back(x2); } else { ee[x2].push_back(y1+n); ee[y1+n].push_back(x2); } } for(int i=1;i<=n+m;i++) { if(f[i]==-1) { f[i]=1; if(dfs(i)) { printf("NO\n"); return ; } } } printf("YES\n"); } int main() { // freopen("1.in","r",stdin); for(int t=read();t;t--) work(); }

当存在 .. .* .. *. *. .. .* .. 时,这个*就需要被覆盖为. 于是大胆dfs一下即可,把样例调过就算成功 int n,m; char s[2010][2010]; void dfs(int x,int y) { if(x*y==0||x>n||y>m||s[x][y]!='*') return ; if((s[x+1][y]=='.'&&s[x+1][y+1]=='.'&&s[x][y+1]=='.') ||(s[x-1][y]=='.'&&s[x-1][y-1]=='.'&&s[x][y-1]=='.') ||(s[x+1][y]=='.'&&s[x+1][y-1]=='.'&&s[x][y-1]=='.') ||(s[x-1][y]=='.'&&s[x-1][y+1]=='.'&&s[x][y+1]=='.')) s[x][y]='.'; else return ; dfs(x+1,y-1); dfs(x+1,y); dfs(x+1,y+1); dfs(x,y-1); dfs(x,y+1); dfs(x-1,y-1); dfs(x-1,y); dfs(x-1,y+1); } int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) scanf("%s",s[i]+1); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(s[i][j]=='*') dfs(i,j); for(int i=1;i<=n;i++) printf("%s\n",s[i]+1); }

dfs会由于栈太大导致re 考虑使用bfs优化之 int n,m; char s[2010][2010]; queue<pair<int,int>>q; int main() { // freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=n;i++) scanf("%s",s[i]+1); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) if(s[i][j]=='*') q.push({i,j}); while(q.size()) { int x=q.front().first; int y=q.front().second; q.pop(); if(x==0||y==0||x>n||y>m||s[x][y]!='*') continue; if((s[x+1][y]=='.'&&s[x+1][y+1]=='.'&&s[x][y+1]=='.')||(s[x-1][y]=='.'&&s[x-1][y-1]=='.'&&s[x][y-1]=='.')||(s[x+1][y]=='.'&&s[x+1][y-1]=='.'&&s[x][y-1]=='.') ||(s[x-1][y]=='.'&&s[x-1][y+1]=='.'&&s[x][y+1]=='.')) s[x][y]='.'; else continue; q.push({x+1,y-1}); q.push({x+1,y}); q.push({x+1,y+1}); q.push({x,y-1}); q.push({x,y+1}); q.push({x-1,y-1}); q.push({x-1,y}); q.push({x-1,y+1}); } for(int i=1;i<=n;i++) printf("%s\n",s[i]+1); }

考虑枚举断电,则问题转化成某个位置i,前面匹配的字符串数量和后面匹配的字符串数量相乘,ac自动机搞一搞即可。 #define N 400010 struct { ll t[N][26],val[N],fail[N],vis[N]; ll cnt=0; void insert(char *a,ll n) { ll u=0; for(ll i=1;i<=n;i++) { ll &v=t[u][a[i]-'a']; if(!v) { cnt++; v=cnt; } u=v; } val[u]++; } void build() { queue<ll>q; for(int i=0;i<26;i++) if(t[0][i]) q.push(t[0][i]); while(q.size()) { ll u=q.front(); q.pop(); for(int i=0;i<26;i++) { ll &v=t[u][i]; if(v) fail[v]=t[fail[u]][i],val[v]+=val[fail[v]],q.push(v); else v=t[fail[u]][i]; } } } void Query(char *a,ll n,ll f[]) { for(ll i=0;i<=cnt;i++) vis[i]=0; ll u=0; for(ll i=1;i<=n;i++) { u=t[u][a[i]-'a']; f[i]=val[u]; } } }ac,Rac; ll f1[N],f2[N]; char a[N],b[N]; int main() { // freopen("1.in","r",stdin); scanf("%s",a+1); ll la=strlen(a+1); for(ll n=read();n;n--) { scanf("%s",b+1); ll lb=strlen(b+1); ac.insert(b,lb); reverse(b+1,b+lb+1); Rac.insert(b,lb); } ac.build(); Rac.build(); ac.Query(a,la,f1); reverse(a+1,a+la+1); Rac.Query(a,la,f2); ll ans=0; for(ll i=1;i<=la;i++) ans+=f1[i]*f2[la-i]; cout<<ans; }

考虑手玩几个,大胆分类讨论,模拟类问题,用cnt维护点数,e维护边数 首先如果全都连通,输出0 如果存在一个独立的点,也就是fa[i]==i&&cnt[i]==1可以对它进行操作,输出1 如果存在一个并查集,并非团,则找一找度数最小的点,他一定不是割点,输出1和这个点 如果全部都是团,则看看团的数量 如果有两个团,则输出siz最小的团里的所有点 如果有多个团,则输出两个不同团里的点 int fa[4010],cnt[4010],n,du[4010],e[4010]; char s[4010][4010]; int get(int x) { return fa[x]==x?x:fa[x]=get(fa[x]); } int print0() { for(int i=1;i<=n;i++) if(get(i)!=get(1)) return 0; cout<<"0\n"; return 1; } int print1() { for(int i=1;i<=n;i++) { if(fa[i]!=i) continue; if(cnt[i]==1) { cout<<1<<'\n'; cout<<i<<'\n'; return 1; } if((cnt[i]*(cnt[i]-1)/2!=e[i])) { int v=i; for(int x=1;x<=n;x++) { if(get(x)==i&&du[x]<du[v]) v=x; } cout<<"1\n"<<v<<'\n'; return 1; } } return 0; } void work() { n=read(); for(int i=1;i<=n;i++) { scanf("%s",s[i]+1); fa[i]=i; cnt[i]=1; e[i]=0; du[i]=0; } for(int i=1;i<=n;i++) { for(int j=1;j<i;j++) { if(s[i][j]=='1') { du[i]++; du[j]++; if(get(i)==get(j)){ e[get(i)]++; continue; } cnt[fa[i]]+=cnt[fa[j]]; e[fa[i]]+=e[fa[j]]+1; fa[fa[j]]=fa[i]; } } } if(print0()) return ; if(print1()) return ; int l=0,r=0; for(int i=1;i<=n;i++) { if(get(i)!=i) continue; if(l==0) l=i; else if(r==0) r=i; else { cout<<2<<'\n'; cout<<l<<' '<<r<<'\n'; return ; } } int v=-1; for(int i=1;i<=n;i++) { if(get(i)!=i) continue; if(v==-1||cnt[i]<cnt[v]) v=i; } cout<<cnt[v]<<'\n'; for(int i=1;i<=n;i++) if(get(i)==v) cout<<i<<' '; cout<<'\n'; } int main() { // freopen("1.in","r",stdin); // freopen("C.out","w",stdout); for(int t=read();t;t--) work();

首先使用莫比乌斯反演,把问题的询问gcd=i改成gcd=i的倍数的链的数量 为了解决这个问题,可以枚举i,把所有a[x]%i=0的点x看做白点,则白点的连通块内任选两点所形成的链都是gcd为i的倍数的链。使用dfs询问siz即可 考虑复杂度,每个数字的因子数量是166320和196560最多,有160个因子。每个点被dfs到的次数为因子数量,故总复杂度为O(160n) const int N=200010; int siz[N],a[N],n; ll g[N],f[N],mu[N]; vector<int>pos[N],yin[N],e[N]; void dfs(int x,int v) { siz[x]=1; for(auto y:e[x]) { if(siz[y]||a[y]%v) continue; dfs(y,v); siz[x]+=siz[y]; } } void Euler() { int Prm[N],vis[N],Pcnt=0; memset(vis,0,sizeof(vis)); mu[1]=1; for(int i=2;i<=N-5;++i){ if(!vis[i]) Prm[++Pcnt]=i,mu[i]=-1; for(int j=1;j<=Pcnt&&i*Prm[j]<=N-5;++j){ vis[i*Prm[j]]=1; if(i%Prm[j]==0) break; mu[i*Prm[j]]=-mu[i]; } } } int main() { // freopen("1.in","r",stdin); for(int i=2;i<=200000;i++) for(int j=i;j<=200000;j+=i) yin[j].push_back(i); n=read(); for(int i=1;i<=n;i++) { a[i]=read(); for(auto v:yin[a[i]]) pos[v].push_back(i); } for(int i=1;i<n;i++) { int x=read(),y=read(); e[x].push_back(y); e[y].push_back(x); } g[1]=n*(n+1ll)/2; for(int i=2;i<=200000;i++) { for(auto x:pos[i]) { if(siz[x]) continue; dfs(x,i); g[i]+=siz[x]*(siz[x]+1ll)/2; } for(auto x:pos[i]) siz[x]=0; } Euler(); for(int i=1;i<=200000;++i) for(int j=i;j<=200000;j+=i) f[i]+=g[j]*mu[j/i]; for(int i=1;i<=200000;i++) if(f[i]) cout<<i<<' '<<f[i]<<'\n'; }

如果-1并非an,则必须贿赂n号 而n号可以为我们最多解决任意n/2个对手 如果这还不够,我们需要从n/2到n里再挑一个人贿赂 找更小的则无法保证必赢 于是以此类推 int n,a[300000]; ll ans; priority_queue<int,vector<int>,greater<int>>q; int main() { // freopen("1.in","r",stdin); n=read(); for(int i=1;i<=n;i++) a[i]=read(); for(int i=n;a[i]!=-1;i--) { q.push(a[i]); if((i&(i-1))==0) { ans=ans+q.top(); q.pop(); } } cout<<ans; }

太强了,还能这样哈希 考虑直接拿着模式串和匹配串匹配复杂度无法接受 于是考虑枚举串长,枚举这个长度的所有哈希值,去和小串进行匹配。则复杂度变为n根号n 套一个unordered set,就做完了 unordered_set<ll>a[300010]; unordered_set<ll>lenlen; int p[300010],f[300010],mod=1000000007; char s[300010]; int main() { // freopen("1.in","r",stdin); p[0]=1; for(int i=1;i<=300000;i++) p[i]=p[i-1]*233ll%mod; for(int t=read();t;t--) { int x=read(); if(x==1) { scanf("%s",s); int len=strlen(s),res=0; for(int i=0;i<len;i++) res=((ll)res*233+s[i])%mod; a[len].insert(res); lenlen.insert(len); } else if(x==2) { scanf("%s",s); int len=strlen(s),res=0; for(int i=0;i<len;i++) res=((ll)res*233+s[i])%mod; a[len].erase(res); } else { scanf("%s",s+1); int n=strlen(s+1),ans=0; for(int i=1;i<=n;i++) f[i]=((ll)f[i-1]*233+s[i])%mod; for(auto len:lenlen) for(int i=len;i<=n;i++) if(a[len].count( ((f[i]-1ll*f[i-len]*p[len])%mod+mod)%mod)) ans++; cout<<ans<<endl; } } }

很妙的构造 首先某个数字出现奇数次一定不行。 否则一定可以 考虑给每一行一对一对的连边 并且给每个数字进行一对一对的连边 然后黑白染色一下 int m,n[100010],cnt,x[200010],y[200010]; string ans[200010]; map<int,vector<int>>pos; vector<int>e[200010]; void dfs(int now) { for(auto nxt:e[now]) { if(ans[x[nxt]][y[nxt]])continue; if(ans[x[now]][y[now]]=='L'){ ans[x[nxt]][y[nxt]]='R'; dfs(nxt); } else { ans[x[nxt]][y[nxt]]='L'; dfs(nxt); } } } int main() { // freopen("1.in","r",stdin); m=read(); for(int i=1;i<=m;i++) { n[i]=read(); // a[i].resize(n[i]); ans[i].resize(n[i]); for(int j=0;j<n[i];j++){ int t=read(); cnt++; x[cnt]=i; y[cnt]=j; pos[t].push_back(cnt); } } for(int i=1;i<cnt;i+=2) { e[i].push_back(i+1); e[i+1].push_back(i); } for(auto o:pos) { if(o.second.size()&1) { cout<<"NO"; return 0; } for(int j=0;j<o.second.size();j+=2) { e[o.second[j]].push_back(o.second[j+1]); e[o.second[j+1]].push_back(o.second[j]); } } for(int i=1;i<=cnt;i++) { if(ans[x[i]][y[i]])continue; ans[x[i]][y[i]]='R'; dfs(i); } cout<<"YES\n"; for(int i=1;i<=m;i++) cout<<ans[i]<<'\n'; }

考虑暴力修改 复杂度n*10000+30*n*logn 跑得飞快 int f[10010],n,m,a[100010],c[100010]; void add(int i,int v) { while(i<=n) { c[i]+=v; i=i+(i&(-i)); } } int ask(int i) { int t=0; while(i) { t+=c[i]; i=i-(i&(-i)); } return t; } int check(int x) { while(x) { if(x%10!=4&&x%10!=7) return 0; x=x/10; } return 1; } char s[10]; int main() { // freopen("1.in","r",stdin); for(int i=1;i<=10000;i++) f[i]=check(i); n=read();m=read(); for(int i=1;i<=n;i++){ a[i]=read(); if(f[a[i]]) add(i,1); } for(;m;m--) { scanf("%s",s); if(s[0]=='c') { int l=read(); cout<<ask(read())-ask(l-1)<<'\n'; } else { int l=read(),r=read(),v=read(); for(int i=l;i<=r;i++) { if(f[a[i]]) add(i,-1); a[i]+=v; if(f[a[i]]) add(i,1); } } } }

如果边abw是合法的 则存在对于xi yi vi 使得dist(xi,a)+w+dist(b,yi)<=vi 也就是-vi+dist(b,yi) <=-w-dist(xi,a) 我们对于固定的xi 预处理出 d[yi]=-vi+dist(x,b) 则对于边abw 判断d[yi]是否<=-w-dist(xi,a)即可 预处理d[yi]复杂度n^3 有了d[yi],扫一遍所有的边,复杂度+n^3 int n,m,q; ll dist[610][610],d[610]; vector<pair<int,int>>e[610]; struct edge { ll x,y,v,ans; }E[360000]; int main() { // freopen("1.in","r",stdin); n=read();m=read(); memset(dist,0x3f,sizeof(dist)); for(int i=1;i<=m;i++) { ll x=read(),y=read(),v=read(); E[i]={x,y,v}; dist[y][x]=dist[x][y]=min(dist[x][y],v); } q=read(); for(int i=1;i<=q;i++) { int x=read(),y=read(),v=read(); e[x].push_back({y,v}); e[y].push_back({x,v}); } for(int x=1;x<=n;x++) dist[x][x]=0; for(int k=1;k<=n;k++) for(int x=1;x<=n;x++) for(int y=1;y<=n;y++) dist[x][y]=min(dist[x][y],dist[x][k]+dist[k][y]); for(int x=1;x<=n;x++) { memset(d,0x3f,sizeof(d)); for(auto y:e[x]) for(int b=1;b<=n;b++) d[b]=min(d[b],-y.second+dist[y.first][b]); for(int i=1;i<=m;i++) if(d[E[i].y]<=-E[i].v-dist[x][E[i].x]||d[E[i].x]<=-E[i].v-dist[x][E[i].y]) E[i].ans=1; } int ans=0; for(int i=1;i<=m;i++) ans=ans+E[i].ans; cout<<ans; }









【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】